DOCSLIB.ORG

Universal Computation in the Prisoner's Dilemma Game Brian Nakayama Regis University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Universal Computation in the Prisoner's Dilemma Game Brian Nakayama Regis University Regis University ePublications at Regis University All Regis University Theses Spring 2013 Universal Computation in the Prisoner's Dilemma Game Brian Nakayama Regis University Follow this and additional works at: https://epublications.regis.edu/theses Part of the Arts and Humanities Commons Recommended Citation Nakayama, Brian, "Universal Computation in the Prisoner's Dilemma Game" (2013). All Regis University Theses. 596. https://epublications.regis.edu/theses/596 This Thesis - Open Access is brought to you for free and open access by ePublications at Regis University. It has been accepted for inclusion in All Regis University Theses by an authorized administrator of ePublications at Regis University. For more information, please contact [email protected]. Regis University Regis College Honors Theses Disclaimer Use of the materials available in the Regis University Thesis Collection (“Collection”) is limited and restricted to those users who agree to comply with the following terms of use. Regis University reserves the right to deny access to the Collection to any person who violates these terms of use or who seeks to or does alter, avoid or supersede the functional conditions, restrictions and limitations of the Collection. The site may be used only for lawful purposes. The user is solely responsible for knowing and adhering to any and all applicable laws, rules, and regulations relating or pertaining to use of the Collection. All content in this Collection is owned by and subject to the exclusive control of Regis University and the authors of the materials. It is available only for research purposes and may not be used in violation of copyright laws or for unlawful purposes. The materials may not be downloaded in whole or in part without permission of the copyright holder or as otherwise authorized in the “fair use” standards of the U.S. copyright laws and regulations. UNIVERSAL COMPUTATION IN THE PRISONER’S DILEMMA GAME A thesis submitted to Regis College The Honors Program in partial fulfillment of the requirements for Graduation with Honors by Brian Nakayama May 2013 ii Contents 1 The Iterated Prisoner’s Dilemma Game 1 1.1 Introducing the G am e........................................................................................ 1 1.2 The Nash Equilibrium and Iterating the G a m e............................................... 4 2 Cellular Automata Theory 8 2.1 What is Cellular Automata?............................................................................... 8 2.2 Cool Cellular Automata..................................................................................... 10 2.3 Universal Computation and Construction: Self-Replicating Machines . 12 2.4 A Review on Literature for the IPDG CA ..................................................... 15 3 Playing the Prisoner’s Dilemma Game with Memory 18 3.1 Giving Each Player “Instructions” .................................................................. 18 3.2 Constructing the Lattice ..................................................................................... 22 3.3 One Interesting Consequence ............................................................................ 25 4 Patterns, Fractals, and Grouping 27 4.1 Creating Order Out of the Randomness............................................................ 27 4.2 How Groups Form ........................................................................................... 34 4.3 Interesting Results ........................................................................................... 35 5 Proof of Universal Computation 39 5.1 Creating a NAND g a t e ..................................................................................... 39 5.2 Making a Computer ........................................................................................... 43 5.3 What this Proof M e a n s .....................................................................................46 6 Social and Biological Relevance 48 6.1 Possible Implications ........................................................................................ 48 iii 6.2 Conclusion ........................................................................................................ 49 7 Further Ideas for Research 52 8 Bibliography 54 iv List of Figures 1 Axelrod's Inequalities for the PDG .................................................................. 3 2 Equations for the IPDG ..................................................................................... 6 3 Rumor Spreading in a Classroom..................................................................... 8 4 Different Wolfram Rules .................................................................................. 10 5 Von Neumann’s Universal Constructor............................................................ 12 6 A Glider Gun and Gliders in the Game of L ife ............................................... 14 7 Composition of Strategy T ypes........................................................................ 19 8 Converting to Base 10 to Make a Strategy Number ...................................... 22 9 A Few Different types of Neighborhoods......................................................... 23 10 Odds of Having a Single Strategy in a Random Initial S tate......................... 25 11 The Effects of the Second N eig h b o r............................................................... 26 12 A 800x600 Random Initial Configuration ..................................................... 27 13 The Hamming Distance..................................................................................... 29 14 4 Iteration Simulation After 750 R ounds......................................................... 30 15 9 Iteration Simulation After 750 R ounds......................................................... 31 16 Cooperating Instructions over Iteratio n s......................................................... 32 17 Point View ........................................................................................................... 34 18 A Natural G un..................................................................................................... 35 19 An Emergent Sierpinski Triangle ..................................................................... 36 20 The Wave Gun .................................................................................................. 37 21 The Three Iteration Gun .................................................................................. 38 22 Randomness Capable of Universal Computation............................................ 39 23 A Glider .............................................................................................................. 39 24 A “Pin” .............................................................................................................. 40 v 25 A Glider Eater.....................................................................................................40 26 Collision Between Two Gliders........................................................................ 41 27 Glider Hooked on a P in .....................................................................................41 28 A NAND Gate made out of IPDG P lay ers..................................................... 42 29 OR and XOR G ates........................................................................................... 43 30 D Latch with a “0” ........................................................................................... 45 31 D Latch with a “1” ........................................................................................... 46 32 A Glider Gun without p i n s ...............................................................................47 vi Picture Credits • Figure 3: Audience in classroom listening intently to speaker during meeting. Har­ less Todd, U.S. Fish and Wildlife Service. Web 08 Aug, 2012. http://www.public- domain-image.com/people-public-domain-images-pictures/crowd-public-domain-images- pictures/audience-in-classroom-listening-intently-to-speaker-during-meeting.jpg.html • Figure 4(Left): Weisstein, Eric W. “Rule 90.” From MathWorld-A Wolfram Web Resource. http://mathworld.wolfram.com/Rule90.html • Figure 4(Middle): Weisstein, Eric W. “Rule 30.” From MathWorld-A Wolfram Web Resource. http://mathworld.wolfram.com/Rule30.html • Figure 4(Right): A Textile Cone Snail. 2005. Richard Ling. Web 08 Aug 2012. http://en.wikipedia.org/wiki/File:Textile_cone.JPG • Figure 5: The Nobili-Pesavento Self-Replicator. 2008. Original automaton: Renato Nobili and Umberto Pesavento. Tape: Tim Hutton; Image: Golly screenshot. Web 22 Sept 2012. http://en.wikipedia.org/wiki/File:Nobili_Pesavento_2reps.png • Figure 6: Created by Brian Nakayama using David Bahr’s Cellular Automaton Ex­ plorer 5.0 • All other images created by Brian Nakayama vii List of Tables 1 The Prisoner’s Dilemma Game in m onths ..................................................... 2 2 The Prisoner’s Dilemma Game........................................................................ 2 3 Cleaning the Dishes P D G .................................................................................. 4 4 3 Memory Transient Strategy for Tit for T a t .................................................. 20 5 3 Memory Asymptotic and Transient Strategy............................................... 21 6 Average Percentage of Initial Cooperators..................................................... 30 7 Average Percentage of Population Points........................................................
Load more

Recommended publications
  • Apparent Entropy of Cellular Automata
    Apparent Entropy of Cellular Automata Bruno Martin Laboratoire d’Informatique et du Parallelisme,´ Ecole´ Normale Superieure´ de Lyon, 46, allee´ d’Italie, 69364 Lyon Cedex 07, France We introduce the notion of apparent entropy on cellular automata that points out how complex some configurations of the space-time diagram may appear to the human eye. We then study, theoretically, if possible, but mainly experimentally through natural examples, the relations between this notion, Wolfram’s intuition, and almost everywhere sensitivity to initial conditions. Introduction A radius-r one-dimensional cellular automaton (CA) is an infinite se- quence of identical finite-state machines (indexed by Ÿ) called cells. Each finite-state machine is in a state and these states change simultane- ously according to a local transition function: the following state of the machine is related to its own state as well as the states of its 2r neigh- bors. A configuration of an automaton is the function which associates to each cell a state. We can thus define a global transition function from the set of all the configurations to itself which associates the following configuration after one step of computation. Recently, a lot of articles proposed classifications of CAs [5, 8, 13] but the canonical reference is still Wolfram’s empirical classification [14] which has resisted numerous attempts of formalization. Among the lat- est attempts, some are based on the mathematical definitions of chaos for dynamical systems adapted to CAs thanks to Besicovitch topol- ogy [2, 6] and [11] introduces the almost everywhere sensitivity to initial conditions for this topology and compares this notion with information propagation formalization.
    [Show full text]
  • Automatic Detection of Interesting Cellular Automata
    Automatic Detection of Interesting Cellular Automata Qitian Liao Electrical Engineering and Computer Sciences University of California, Berkeley Technical Report No. UCB/EECS-2021-150 http://www2.eecs.berkeley.edu/Pubs/TechRpts/2021/EECS-2021-150.html May 21, 2021 Copyright © 2021, by the author(s). All rights reserved. Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission. Acknowledgement First I would like to thank my faculty advisor, professor Dan Garcia, the best mentor I could ask for, who graciously accepted me to his research team and constantly motivated me to be the best scholar I could. I am also grateful to my technical advisor and mentor in the field of machine learning, professor Gerald Friedland, for the opportunities he has given me. I also want to thank my friend, Randy Fan, who gave me the inspiration to write about the topic. This report would not have been possible without his contributions. I am further grateful to my girlfriend, Yanran Chen, who cared for me deeply. Lastly, I am forever grateful to my parents, Faqiang Liao and Lei Qu: their love, support, and encouragement are the foundation upon which all my past and future achievements are built. Automatic Detection of Interesting Cellular Automata by Qitian Liao Research Project Submitted to the Department of Electrical Engineering and Computer Sciences, University of California at Berkeley, in partial satisfaction of the requirements for the degree of Master of Science, Plan II.
    [Show full text]
  • Arxiv:1607.02291V3 [Cs.FL] 8 May 2018
    Noname manuscript No. (will be inserted by the editor) A Survey of Cellular Automata: Types, Dynamics, Non-uniformity and Applications (Draft version) Kamalika Bhattacharjee · Nazma Naskar · Souvik Roy · Sukanta Das Received: date / Accepted: date Abstract Cellular automata (CAs) are dynamical systems which exhibit complex global be- havior from simple local interaction and computation. Since the inception of cellular au- tomaton (CA) by von Neumann in 1950s, it has attracted the attention of several researchers over various backgrounds and fields for modelling different physical, natural as well as real- life phenomena. Classically, CAs are uniform. However, non-uniformity has also been in- troduced in update pattern, lattice structure, neighborhood dependency and local rule. In this survey, we tour to the various types of CAs introduced till date, the different characteriza- tion tools, the global behaviors of CAs, like universality, reversibility, dynamics etc. Special attention is given to non-uniformity in CAs and especially to non-uniform elementary CAs, which have been very useful in solving several real-life problems. Keywords Cellular Automata (CAs) · Types · Characterization tools · Dynamics · Non-uniformity · Technology Mathematics Subject Classification (2010) 68Q80 · 37B15 1 Introduction From the end of the first half of 20th century, a new approach has started to come in scien- tific studies, which after questioning the so called Cartesian analytical approach, says that interconnections among the elements of a system, be it physical, biological, artificial or any other, greatly effect the behavior of the system. In fact, according to this approach, knowing the parts of a system, one can not properly understand the system as a whole.
    [Show full text]
  • Complexity Properties of the Cellular Automaton Game of Life
    Portland State University PDXScholar Dissertations and Theses Dissertations and Theses 11-14-1995 Complexity Properties of the Cellular Automaton Game of Life Andreas Rechtsteiner Portland State University Follow this and additional works at: https://pdxscholar.library.pdx.edu/open_access_etds Part of the Physics Commons Let us know how access to this document benefits ou.y Recommended Citation Rechtsteiner, Andreas, "Complexity Properties of the Cellular Automaton Game of Life" (1995). Dissertations and Theses. Paper 4928. https://doi.org/10.15760/etd.6804 This Thesis is brought to you for free and open access. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. THESIS APPROVAL The abstract and thesis of Andreas Rechtsteiner for the Master of Science in Physics were presented November 14th, 1995, and accepted by the thesis committee and the department. COMMITTEE APPROVALS: 1i' I ) Erik Boaegom ec Representativi' of the Office of Graduate Studies DEPARTMENT APPROVAL: **************************************************************** ACCEPTED FOR PORTLAND STATE UNNERSITY BY THE LIBRARY by on /..-?~Lf!c-t:t-?~~ /99.s- Abstract An abstract of the thesis of Andreas Rechtsteiner for the Master of Science in Physics presented November 14, 1995. Title: Complexity Properties of the Cellular Automaton Game of Life The Game of life is probably the most famous cellular automaton. Life shows all the characteristics of Wolfram's complex Class N cellular automata: long-lived transients, static and propagating local structures, and the ability to support universal computation. We examine in this thesis questions about the geometry and criticality of Life.
    [Show full text]
  • Dipl. Eng. Thesis
    A Framework for the Real-Time Execution of Cellular Automata on Reconfigurable Logic By NIKOLAOS KYPARISSAS Microprocessor & Hardware Laboratory School of Electrical & Computer Engineering TECHNICAL UNIVERSITY OF CRETE A thesis submitted to the Technical University of Crete in accordance with the requirements for the DIPLOMA IN ELECTRICAL AND COMPUTER ENGINEERING. FEBRUARY 2020 THESIS COMMITTEE: Prof. Apostolos Dollas, Technical University of Crete, Thesis Supervisor Prof. Dionisios Pnevmatikatos, National Technical University of Athens Prof. Michalis Zervakis, Technical University of Crete ABSTRACT ellular automata are discrete mathematical models discovered in the 1940s by John von Neumann and Stanislaw Ulam. They constitute a general paradigm for massively parallel Ccomputation. Through time, these powerful mathematical tools have been proven useful in a variety of scientific fields. In this thesis we propose a customizable parallel framework on reconfigurable logic which can be used to efficiently simulate weighted, large-neighborhood totalistic and outer-totalistic cellular automata in real time. Simulating cellular automata rules with large neighborhood sizes on large grids provides a new aspect of modeling physical processes with realistic features and results. In terms of performance results, our pipelined application-specific architecture successfully surpasses the computation and memory bounds found in a general-purpose CPU and has a measured speedup of up to 51 against an Intel Core i7-7700HQ CPU running highly optimized £ software programmed in C. i ΠΕΡΙΛΗΨΗ α κυψελωτά αυτόματα είναι διακριτά μαθηματικά μοντέλα που ανακαλύφθηκαν τη δεκαετία του 1940 από τον John von Neumann και τον Stanislaw Ulam. Αποτελούν ένα γενικό Τ υπόδειγμα υπολογισμών με εκτενή παραλληλισμό. Μέχρι σήμερα τα μαθηματικά αυτά εργαλεία έχουν χρησιμεύσει σε πληθώρα επιστημονικών τομέων.
    [Show full text]
  • Abstract Collection of the 2017 International Symposium on Nonlinear Theory and Its Applications (NOLTA2017)
    Abstract Collection of the 2017 International Symposium on Nonlinear Theory and its Applications (NOLTA2017) Cancun International Convention Center, Cancun,´ Mexico December 4–7, 2017. Abstract Collection of NOLTA2017 ⃝C IEICE Japan 2017 Typesetting: Data conversion by the authors. Final processing by T. Tsubone and W. Kurebayashi with LATEX. Printed in Japan 2 Contents Welcome Message from the General Chairs . 6 Technical Program Chair’s Message . 7 Organizing Committee . 8 Technical Program Committee . 9 Advisory Committee . 10 NOLTA Steering Committee . 11 Special Session Organizers . 12 Symposium Information . 14 Symposium Venue . 14 Social Events . 14 Session at a Glance . 16 Abstracts 19 A0L-A Plenary Talk 1 . 19 A1L-A Theory and Learning Applications of Koopman Operator Formalism . 19 A1L-B Systems Theory and its Applications . 20 A1L-C Complex systems, complex networks and bigdata analyses . 21 A1L-D Advanced Theory and Applications Related to Communication Quality . 23 A1L-E Neuromorphic Systems and Electronic Devices 1 . 24 A2L-A Network Function for Physically and Logically Coupled System . 25 A2L-B Circuits and Systems / Analog and digital devices . 26 A2L-C Neural Networks / Biological Engineering . 27 A2L-D Complex Communication Sciences 1 . 28 A2L-E Neuromorphic Systems and Electronic Devices 2 . 29 A3L-A Radio and Optical Wireless Communications 1 . 30 A3L-B Complex Networks and Systems / Image and Signal Processing . 32 A3L-C Laser Dynamics and Complex Photonics 1 . 34 A3L-D-1 Complex Communication Sciences 2 . 35 A3L-D-2 Complex Networks and Systems / Image and Signal Processing . 36 A3L-E-1 Neuromorphic Systems and Electronic Devices 3 . 37 A3L-E-2 Machine Learning / Evolutionary computations .
    [Show full text]
  • Lecture P4: Cellular Automata Arrays Allow Manipulation of Potentially Huge Amounts of Data
    Array Review Lecture P4: Cellular Automata Arrays allow manipulation of potentially huge amounts of data. ■ All elements of the same type. – double, int ■ N-element array has elements indexed 0 through N-1. ■ Fast access to arbitrary element. – a[i] ■ Waste of space if array is "sparse." Reaction diffusion textures. Andy Witkin and Michael Kass Princeton University • COS 126 • General Computer Science • Fall 2002 • http://www.Princeton.EDU/~cs126 2 Cellular Automata Applications of Cellular Automata Cellular automata. (singular = cellular automaton) Modern applications. ■ Computer simulations that try to emulate laws of nature. ■ Simulations of biology, chemistry, physics. ■ Simple rules can generate complex patterns. – ferromagnetism according to Ising mode – forest fire propagation – nonlinear chemical reaction-diffusion systems – turbulent flow John von Neumann. (Princeton IAS, 1950s) – biological pigmentation patterns ■ Wanted to create and simulate artificial – breaking of materials life on a machine. – growth of crystals ■ Self-replication. – growth of plants and animals ■ ■ "As simple as possible, but no simpler." Image processing. ■ Computer graphics. ■ Design of massively parallel hardware. ■ Art. 3 4 How Did the Zebra Get Its Stripes? One Dimensional Cellular Automata 1-D cellular automata. ■ Sequence of cells. ■ Each cell is either black (alive) or white (dead). ■ In each time step, update status of each cell, depending on color of nearby cells from previous time step. Example rule. Make cell black at time t if at least one of its proper neighbors was black at time t-1. time 0 time 1 time 2 Synthetic zebra. Greg Turk 5 6 Cellular Automata: Designing the Code Cellular Automata: The Code How to store the row of cells.
    [Show full text]
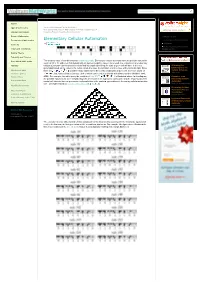
  • Elementary Cellular Automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations >
    Search MathWorld Algebra Applied Mathematics Discrete Mathematics > Cellular Automata > Recreational Mathematics > Mathematical Art > Mathematical Images > elementary cellular automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations > Discrete Mathematics THINGS TO TRY: Foundations of Mathematics Elementary Cellular Automaton elementary cellular automaton 39th prime Geometry do the algebraic units contain History and Terminology Sqrt[2]+Sqrt[3]? Number Theory Probability and Statistics Recreational Mathematics The simplest class of one-dimensional cellular automata. Elementary cellular automata have two possible values for each cell (0 or 1), and rules that depend only on nearest neighbor values. As a result, the evolution of an elementary Topology cellular automaton can completely be described by a table specifying the state a given cell will have in the next A Strategy for generation based on the value of the cell to its left, the value the cell itself, and the value of the cell to its right. Since Exploring k=2, r=2 Alphabetical Index there are possible binary states for the three cells neighboring a given cell, there are a total of Cellular Automata John Kiehl Interactive Entries elementary cellular automata, each of which can be indexed with an 8-bit binary number (Wolfram 1983, Random Entry 2002). For example, the table giving the evolution of rule 30 ( ) is illustrated above. In this diagram, Dynamics of an the possible values of the three neighboring cells are shown in the top row of each panel, and the resulting value the Elementary Cellular New in MathWorld central cell takes in the next generation is shown below in the center. generations of elementary cellular automaton Automaton rule are implemented as CellularAutomaton[r, 1 , 0 , n].
    [Show full text]
  • Controls on Video Rental Eased
    08120 A RETAILER'S L, GUIDE TO HO-ME NEWSPAPER BB049GREENL YMDNT00 t4AR83 MONTY GREENLY 03 1 C UCY 3740 ELM LONG BEACH CA 90807 A Billboard Publication w & w Entertainment The International Newsweekly Of Music Home Aug. 28, 1982 $3 (U.S.) VIA FOUR CHAINS Controls On Video Rental Eased Impact Of Price Cut On Less Rental -Only Titles; Warner Drops `Choice' Plan Tapes Tested At Retail By LAURA FOTI shows how rental -only plans have The "B" and "lease /purchase" been revised and what effect the re- classifications have been dropped. By JOHN SIPF EL LOS ANGELES major Key retail executives at NEW YORK -Major studios are visions are having at retail. The "Dealer's Choice" program -Four con.inually. retail chains hope to prove for man- the meeting, however, also com- fast relinquishing control over home Warner Home Video, for ex- was instituted in January, after a na- that dramatically lower mer_ted that LPs' decline in numbers video rental programs. More and ample, has dropped its "Dealer's tional outcry against the original ufacturers list prices on prerecorded tape can at tLe sales register is not being com- more, dealers are selling or renting at Choice" program, with its three -tier Warner Home Video rental -only increase sales. pensated for by the cassettes' their option regardless of restrictions title classification and lease /pur- plan launched in October, 1981. The substantially Single Camelot, Tower, Western growth. imposed when product was ac- chase plan. While the company still revised version was said by dealers Merchandising and Flipside (Chi- (Continued on page 15) quired, with little or no interference has rental -only titles, their release to be extremely complex, although it stores are currently carrying from manufacturers.
    [Show full text]
  • Global Properties of Cellular Automata
    Global properties of cellular automata Edward Jack Powley Submitted for the qualification of PhD University of York Department of Computer Science October 2009 Abstract A cellular automaton (CA) is a discrete dynamical system, composed of a large number of simple, identical, uniformly interconnected components. CAs were introduced by John von Neumann in the 1950s, and have since been studied extensively both as models of real-world systems and in their own right as abstract mathematical and computational systems. CAs can exhibit emergent behaviour of varying types, including universal computation. As is often the case with emergent behaviour, predicting the behaviour from the specification of the system is a nontrivial task. This thesis explores some properties of CAs, and studies the correlations between these properties and the qualitative behaviour of the CA. The properties studied in this thesis are properties of the global state space of the CA as a dynamical system. These include degree of symmetry, numbers of preimages (convergence of trajectories), and distances between successive states on trajectories. While we do not obtain a complete classifi- cation of CAs according to their qualitative behaviour, we argue that these types of global properties are a better indicator than other, more local, properties. 3 Contents Chapter 1. Introduction 11 Part 1. Literature review 15 Chapter 2. Cellular automata 17 2.1. Definition and dynamics 17 2.2. Example: Conway's Game of Life 19 2.3. 1-dimensional CAs and elementary CAs 21 2.4. Essentially different rules 23 2.5. Classification 26 2.6. Speed of propagation 29 2.7.
    [Show full text]
  • Symbiosis Promotes Fitness Improvements in the Game of Life
    Symbiosis Promotes Fitness Peter D. Turney* Ronin Institute Improvements in the [email protected] Game of Life Keywords Symbiosis, cooperation, open-ended evolution, Game of Life, Immigration Game, levels of selection Abstract We present a computational simulation of evolving entities that includes symbiosis with shifting levels of selection. Evolution by natural selection shifts from the level of the original entities to the level of the new symbiotic entity. In the simulation, the fitness of an entity is measured by a series of one-on-one competitions in the Immigration Game, a two-player variation of Conwayʼs Game of Life. Mutation, reproduction, and symbiosis are implemented as operations that are external to the Immigration Game. Because these operations are external to the game, we can freely manipulate the operations and observe the effects of the manipulations. The simulation is composed of four layers, each layer building on the previous layer. The first layer implements a simple form of asexual reproduction, the second layer introduces a more sophisticated form of asexual reproduction, the third layer adds sexual reproduction, and the fourth layer adds symbiosis. The experiments show that a small amount of symbiosis, added to the other layers, significantly increases the fitness of the population. We suggest that the model may provide new insights into symbiosis in biological and cultural evolution. 1 Introduction There are two main definitions of symbiosis in biology, (1) symbiosis as any association and (2) symbiosis as persistent mutualism [7]. The first definition allows any kind of persistent contact between different species of organisms to count as symbiosis, even if the contact is pathogenic or parasitic.
    [Show full text]
  • 5 Cellular Automata Models
    5 Cellular automata models Cellular automata (CA) models epitomize the idea that simple rules can generate complex patterns. A CA consists of an array of cells each with an integer 'state'. On each time step a local update rule is applied to the cells. The update rule defines how the a particular cell will update its state as a funcion of its neighbours state. The CA is run over time and the evolution of the state is observed. 5.1 Elementary cellular automata The elementary one dimensional CA is defined by how three cells influence a single cell. For example, The rules can be expressed in binary form where a 0 represents that a par- ticular configuration gives a white output and a 1 denotes a black output. For example, the above rule in binary is 00011110. Converting this binary number to base-10, we call this rule 30. We thus have a set of different rules for elementary cellular automata from 0 up to 255. 21 Although the rule itself is simple, the output of rule 30 is somewhat compli- cated. 22 23 Elementary CA simulators are easily found on the internet. In the lecture, I will demonstrate one of these written in NetLogo (http://ccl.northwestern.edu/netlogo/). We will look at rules 254, 250, 150, 90, 110, 30 and 193 in this simulator. Some of these rules produce simple repetitive patterns, others produce pe- riodic patterns, while some produce complicated patterns. Rule 30 is of special interest because it is chaotic. This rule is used as the random number generator used for large integers in Mathematica.
    [Show full text]