A Note on Masking Generic Boolean Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Designing PCI Cards and Drivers for Power Macintosh Computers
Designing PCI Cards and Drivers for Power Macintosh Computers Revised Edition Revised 3/26/99 Technical Publications © Apple Computer, Inc. 1999 Apple Computer, Inc. Adobe, Acrobat, and PostScript are Even though Apple has reviewed this © 1995, 1996 , 1999 Apple Computer, trademarks of Adobe Systems manual, APPLE MAKES NO Inc. All rights reserved. Incorporated or its subsidiaries and WARRANTY OR REPRESENTATION, EITHER EXPRESS OR IMPLIED, WITH No part of this publication may be may be registered in certain RESPECT TO THIS MANUAL, ITS reproduced, stored in a retrieval jurisdictions. QUALITY, ACCURACY, system, or transmitted, in any form America Online is a service mark of MERCHANTABILITY, OR FITNESS or by any means, mechanical, Quantum Computer Services, Inc. FOR A PARTICULAR PURPOSE. AS A electronic, photocopying, recording, Code Warrior is a trademark of RESULT, THIS MANUAL IS SOLD “AS or otherwise, without prior written Metrowerks. IS,” AND YOU, THE PURCHASER, ARE permission of Apple Computer, Inc., CompuServe is a registered ASSUMING THE ENTIRE RISK AS TO except to make a backup copy of any trademark of CompuServe, Inc. ITS QUALITY AND ACCURACY. documentation provided on Ethernet is a registered trademark of CD-ROM. IN NO EVENT WILL APPLE BE LIABLE Xerox Corporation. The Apple logo is a trademark of FOR DIRECT, INDIRECT, SPECIAL, FrameMaker is a registered Apple Computer, Inc. INCIDENTAL, OR CONSEQUENTIAL trademark of Frame Technology Use of the “keyboard” Apple logo DAMAGES RESULTING FROM ANY Corporation. (Option-Shift-K) for commercial DEFECT OR INACCURACY IN THIS purposes without the prior written Helvetica and Palatino are registered MANUAL, even if advised of the consent of Apple may constitute trademarks of Linotype-Hell AG possibility of such damages. -

Faster Base64 Encoding and Decoding Using AVX2 Instructions
Faster Base64 Encoding and Decoding using AVX2 Instructions WOJCIECH MUŁA, DANIEL LEMIRE, Universite´ du Quebec´ (TELUQ) Web developers use base64 formats to include images, fonts, sounds and other resources directly inside HTML, JavaScript, JSON and XML files. We estimate that billions of base64 messages are decoded every day. We are motivated to improve the efficiency of base64 encoding and decoding. Compared to state-of-the-art implementations, we multiply the speeds of both the encoding (≈ 10×) and the decoding (≈ 7×). We achieve these good results by using the single-instruction-multiple-data (SIMD) instructions available on recent Intel processors (AVX2). Our accelerated software abides by the specification and reports errors when encountering characters outside of the base64 set. It is available online as free software under a liberal license. CCS Concepts: •Theory of computation ! Vector / streaming algorithms; General Terms: Algorithms, Performance Additional Key Words and Phrases: Binary-to-text encoding, Vectorization, Data URI, Web Performance 1. INTRODUCTION We use base64 formats to represent arbitrary binary data as text. Base64 is part of the MIME email protocol [Linn 1993; Freed and Borenstein 1996], used to encode binary attachments. Base64 is included in the standard libraries of popular programming languages such as Java, C#, Swift, PHP, Python, Rust, JavaScript and Go. Major database systems such as Oracle and MySQL include base64 functions. On the Web, we often combine binary resources (images, videos, sounds) with text- only documents (XML, JavaScript, HTML). Before a Web page can be displayed, it is often necessary to retrieve not only the HTML document but also all of the separate binary resources it needs. -

Bit-Mask Based Compression of FPGA Bitstreams
International Journal of Soft Computing and Engineering (IJSCE) ISSN: 2231-2307, Volume-3 Issue-1, March 2013 Bit-Mask Based Compression of FPGA Bitstreams S.Vigneshwaran, S.Sreekanth The efficiency of bitstream compression is measured using Abstract— In this paper, bitmask based compression of FPGA Compression Ratio (CR). It is defined as the ratio between the bit-streams has been implemented. Reconfiguration system uses compressed bitstream size (CS) and the original bitstream bitstream compression to reduce bitstream size and memory size (OS) (ie CR=CS/OS). A smaller compression ratio requirement. It also improves communication bandwidth and implies a better compression technique. Among various thereby decreases reconfiguration time. The three major compression techniques that has been proposed compression contributions of this paper are; i) Efficient bitmask selection [5] seems to be attractive for bitstream compression, because technique that can create a large set of matching patterns; ii) Proposes a bitmask based compression using the bitmask and of its good compression ratio and relatively simple dictionary selection technique that can significantly reduce the decompression scheme. This approach combines the memory requirement iii) Efficient combination of bitmask-based advantages of previous compression techniques with good compression and G o l o m b coding of repetitive patterns. compression ratio and those with fast decompression. Index Terms—Bitmask-based compression, Decompression II. RELATED WORK engine, Golomb coding, Field Programmable Gate Array (FPGA). The existing bitstream compression techniques can be classified into two categories based on whether they need I. INTRODUCTION special hardware support during decompression. Some Field-Programmable Gate Arrays (Fpga) is widely used in approaches require special hardware features to access the reconfigurable systems. -

Chapter 17: Filters to Detect, Filters to Protect Page 1 of 11
Chapter 17: Filters to Detect, Filters to Protect Page 1 of 11 Chapter 17: Filters to Detect, Filters to Protect You learned about the concepts of discovering events of interest by configuring filters in Chapter 8, "Introduction to Filters and Signatures." That chapter showed you various different products with unique filtering languages to assist you in discovering malicious types of traffic. What if you are a do- it-yourself type, inclined to watch Bob Vila or "Men in Tool Belts?" The time-honored TCPdump program comes with an extensive filter language that you can use to look at any field, combination of fields, or bits found in an IP datagram. If you like puzzles and don’t mind a bit of tinkering, you can use TCPdump filters to extract different anomalous traffic. Mind you, this is not the tool for the faint of heart or for those of you who shy away from getting your brain a bit frazzled. Those who prefer a packaged solution might be better off using the commercial products and their GUIs or filters. This chapter introduces the concept of using TCPdump and TCPdump filters to detect events of interest. TCPdump and TCPdump filters are the backbone of Shadow, and so the recommended suggestion is to download the current version of Shadow at http://www.nswc.navy.mil/ISSEC/CID/ to examine and enhance its native filters. This takes care of automating the collection and processing of traffic, freeing you to concentrate on improving the TCPdump filters for better detects. Specifically, this chapter discusses the mechanics of creating TCPdump filters. -

This Is a Free, User-Editable, Open Source Software Manual. Table of Contents About Inkscape
This is a free, user-editable, open source software manual. Table of Contents About Inkscape....................................................................................................................................................1 About SVG...........................................................................................................................................................2 Objectives of the SVG Format.................................................................................................................2 The Current State of SVG Software........................................................................................................2 Inkscape Interface...............................................................................................................................................3 The Menu.................................................................................................................................................3 The Commands Bar.................................................................................................................................3 The Toolbox and Tool Controls Bar........................................................................................................4 The Canvas...............................................................................................................................................4 Rulers......................................................................................................................................................5 -

Chapter 4 Data-Level Parallelism in Vector, SIMD, and GPU Architectures
Computer Architecture A Quantitative Approach, Fifth Edition Chapter 4 Data-Level Parallelism in Vector, SIMD, and GPU Architectures Copyright © 2012, Elsevier Inc. All rights reserved. 1 Contents 1. SIMD architecture 2. Vector architectures optimizations: Multiple Lanes, Vector Length Registers, Vector Mask Registers, Memory Banks, Stride, Scatter-Gather, 3. Programming Vector Architectures 4. SIMD extensions for media apps 5. GPUs – Graphical Processing Units 6. Fermi architecture innovations 7. Examples of loop-level parallelism 8. Fallacies Copyright © 2012, Elsevier Inc. All rights reserved. 2 Classes of Computers Classes Flynn’s Taxonomy SISD - Single instruction stream, single data stream SIMD - Single instruction stream, multiple data streams New: SIMT – Single Instruction Multiple Threads (for GPUs) MISD - Multiple instruction streams, single data stream No commercial implementation MIMD - Multiple instruction streams, multiple data streams Tightly-coupled MIMD Loosely-coupled MIMD Copyright © 2012, Elsevier Inc. All rights reserved. 3 Introduction Advantages of SIMD architectures 1. Can exploit significant data-level parallelism for: 1. matrix-oriented scientific computing 2. media-oriented image and sound processors 2. More energy efficient than MIMD 1. Only needs to fetch one instruction per multiple data operations, rather than one instr. per data op. 2. Makes SIMD attractive for personal mobile devices 3. Allows programmers to continue thinking sequentially SIMD/MIMD comparison. Potential speedup for SIMD twice that from MIMID! x86 processors expect two additional cores per chip per year SIMD width to double every four years Copyright © 2012, Elsevier Inc. All rights reserved. 4 Introduction SIMD parallelism SIMD architectures A. Vector architectures B. SIMD extensions for mobile systems and multimedia applications C. -

X86 Intrinsics Cheat Sheet Jan Finis [email protected]
x86 Intrinsics Cheat Sheet Jan Finis [email protected] Bit Operations Conversions Boolean Logic Bit Shifting & Rotation Packed Conversions Convert all elements in a packed SSE register Reinterpet Casts Rounding Arithmetic Logic Shift Convert Float See also: Conversion to int Rotate Left/ Pack With S/D/I32 performs rounding implicitly Bool XOR Bool AND Bool NOT AND Bool OR Right Sign Extend Zero Extend 128bit Cast Shift Right Left/Right ≤64 16bit ↔ 32bit Saturation Conversion 128 SSE SSE SSE SSE Round up SSE2 xor SSE2 and SSE2 andnot SSE2 or SSE2 sra[i] SSE2 sl/rl[i] x86 _[l]rot[w]l/r CVT16 cvtX_Y SSE4.1 cvtX_Y SSE4.1 cvtX_Y SSE2 castX_Y si128,ps[SSE],pd si128,ps[SSE],pd si128,ps[SSE],pd si128,ps[SSE],pd epi16-64 epi16-64 (u16-64) ph ↔ ps SSE2 pack[u]s epi8-32 epu8-32 → epi8-32 SSE2 cvt[t]X_Y si128,ps/d (ceiling) mi xor_si128(mi a,mi b) mi and_si128(mi a,mi b) mi andnot_si128(mi a,mi b) mi or_si128(mi a,mi b) NOTE: Shifts elements right NOTE: Shifts elements left/ NOTE: Rotates bits in a left/ NOTE: Converts between 4x epi16,epi32 NOTE: Sign extends each NOTE: Zero extends each epi32,ps/d NOTE: Reinterpret casts !a & b while shifting in sign bits. right while shifting in zeros. right by a number of bits 16 bit floats and 4x 32 bit element from X to Y. Y must element from X to Y. Y must from X to Y. No operation is SSE4.1 ceil NOTE: Packs ints from two NOTE: Converts packed generated. -

Simplified Adaptive Multiplicative Masking For
Simplified Adaptive Multiplicative Masking for AES Elena Trichina, Domenico De Seta, and Lucia Germani Cryptographic Design Center, Gemplus TechnologyR&D Via Pio Emanuelli 1, 00143 Rome, Italy {elena.trichina,domenico.deseta,lucia.germani}@gemplus.com Abstract. Software counter measures against side channel attacks con- siderably hinder performance of cryptographic algorithms in terms of memory or execution time or both. The challenge is to achieve secure implementation with as little extra cost as possible. In this paper we optimize a counter measure for the AES block cipher consisting in trans- forming a boolean mask to a multiplicative mask prior to a non-linear Byte Substitution operation (thus, avoiding S-box re-computations for every run or storing multiple S-box tables in RAM), while preserving a boolean mask everywhere else. We demonstrate that it is possible to achieve such transformation for a cost of two additional multiplications in the field. However, due to an inherent vulnerability of multiplicative masking to so-called zero attack, an additional care must be taken to securize its im- plementation. We describe one possible, although not perfect, approach to such an implementation which combines algebraic techniques and par- tial re-computation of S-boxes. This adds one more multiplication oper- ation, and either occasional S-box re-computations or extra 528 bytes of memory to the total price of the counter measure. 1 Introduction With the increasing research endeavors in the field of side-channel attacks both hardware and software implementations of cryptosystems have to take into ac- count various counter measures. The main techniques are timing attacks [10], simple (SPA) and differential power analysis (DPA) [11], and electromagnetic attacks [7] . -
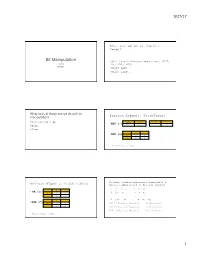
Bit Manipulation.Pptx
9/27/17 What can we do at the bit level? Bit Manipula+on • (bit level) Boolean operations (NOT, CS 203 OR, AND, XOR) Fall 2017 • Shift left • Shift right 1 2 What sorts of things can we do with bit manipula+on? Boolean Algebra: TruthTables • Multiply/divide False True 0 1 • NOT (~) • Mask True False 1 0 • Swap • 0 1 AND (&) 0 0 0 1 0 1 Where: 0 = False; 1 = True 3 4 Boolean algebra and binary manipulation: Boolean Algebra: Truth Tables Bitwise application of Boolean algebra X = [xn-1 xn-2 … x2 x1 x0] 0 1 • OR (|) Y = [y y … y y y ] 0 0 1 n-1 n-2 2 1 0 ---------------------------------------------------------- 1 1 1 ~X = [~x ~x … ~x ~x ~x ] 0 1 n-1 n-2 2 1 0 • XOR (^) 0 0 1 X&Y = [(xn-1&yn-1) (xn-2&yn-2) … (x1&y1) (x0&y0)] 1 1 0 X|Y = [(xn-1|yn-1) (xn-2|yn-2) … (x1|y1) (x0|y0)] X^Y = [(xn-1^yn-1) (xn-2^yn-2) … (x1^y1) (x0^y0)] Where: 0 = False; 1 = True 5 6 1 9/27/17 Boolean algebra and binary manipulation: Boolean algebra and binary manipulation: Bitwise application of Boolean algebra Bitwise application of Boolean algebra • Given X = [00101111]; Y = [10111000] • Given X = [00101111];Y = [10111000] • ~X = ? • X&Y = ? • ~X = [11010000] X&Y = [00101000] • X|Y = ? • X^Y = ? • X|Y =[10111111] X^Y = [10010111] 7 8 Subtracting by adding: 2’s Using 2’s complement to complement subtract by adding • X – Y = X + (-Y) make use of this fact!!! • 5 – 3 • 1’s complement --- flip the bits [00000101] – [00000011] • 2’s complement of a number is the 1’s complement + 1 = [00000101] + 2’s complement ([00000011]) = [00000101] + ([11111100] + [00000001]) [00000000] = [00000101] + [11111101] 1’s complement [11111111] = [00000010] = 2 2’s complement [00000000] 10 When using 2’s complement, do not have the 2- zero issue 9 10 What can we do?: What can we do?: XOR as a programmable inverter Masking • Given a bit a; how you set it determines whether • A series of bits (word, half-word, etc.) can act as a another bit b is inverted (flipped) or left mask unchanged. -

Efficient Binary and Run Length Morphology and Its Application To
Efficient Binary and Run Length Morphology and its Application to Document Image Processing Thomas M. Breuel DFKI and U. Kaiserslautern [email protected] Abstract This paper describes the implementation and evaluation of an open source library for mathematical morphology based on packed binary and run-length compressed images for document imaging applications. Ab- stractions and patterns useful in the implementation of the interval oper- ations are described. A number of benchmarks and comparisons to bit-blit based implementations on standard document images are provided. 1 Introduction Binary morphology is an important and widely used method in document im- age analysis, useful for tasks like image cleaning and noise removal, [24] layout analysis, [23] skew correction, [15] and text line finding. [6] Real-world doc- ument analysis systems currently primarily rely on bit blit-based implementa- tions. Practical implementations take advantage of separability and logarithmic decomposition of rectangular structuring elements [19, 4, 15]. This technical report describes a binary morphology library containing both a run-length and a packed binary implementation of morphological operations. A number of the methods described in this paper are very similar to methods described in the literature [13, 19], although the library was developed inde- pently of that literature. The paper will not provide a detailed discussion of the arXiv:0712.0121v1 [cs.GR] 2 Dec 2007 similarities and differences of the algorithms described in this memo to those in the literature1 This memo does provide a number of benchmarks that should help practitioners choose good algorithms for their particular applications. We note that, in addition to run length and packed binary methods, a num- ber of other methods have been described in the literature. -

Cpre 288 – Introduction to Embedded Systems
CprE 288 – Introduction to Embedded Systems Instructors: Dr. Phillip Jones http://class.ece.iastate.edu/cpre288 1 Announcements • HW 5: Due Sunday (9/26) • Quiz 5: Tuesday (9/28) – First 10 minutes of class using Canvas – Class lectures – HW 4 & 5 material – Notes: Once sheet of notes (1-side) • Quiz 4: This Thursday http://class.ece.iastate.edu/cpre288 2 4 BITWISE OPERATIONS http://class.ece.iastate.edu/cpre288 10 Why Bitwise Operation Why use bitwise operations in embedded systems programming? Each single bit may have its own meaning – Push button array: Bit n is 0 if push button n is pushed – LED array: Set bit n to 0 to light LED n Data from/to I/O ports may be packed – Two bits for shaft encoder, six bits for push button packed in PINC – Keypad input: three bits for row position, three bits for column position Data in memory may be packed to save space – Split one byte into two 4-bit integers http://class.ece.iastate.edu/cpre288 11 Why Bitwise Operation Read the input: GPIO_PORTE_R; How to have application determine which button is being pushed? SW4 SW3 SW2 SW1 Bit 3 Bit 2 Bit 1 Bit 0 Buttons connected to PORTE, bits 3-0 http://class.ece.iastate.edu/cpre288 12 Bitwise Operations Common programming tasks: • Clear/Reset certain bit(s) • Set certain bit(s) • Test if certain bit(s) are cleared/reset • Test if certain bit(s) are set • Toggle/invert certain bits • Shift bits around http://class.ece.iastate.edu/cpre288 13 Bitwise Operators: Clear/Force-to-0 Bits C bitwise AND: & ch = ch & 0x3C; What does it do? Preserve Consider a single -

6.172 Performance Engineering of Software Systems, Lecture 3: Bit Hacks
6.172 Performance !"##$* Engineering %&'&( of Software Systems "#)*+)$#)*+,*-./01* LECTURE 3 ! Bit Hacks Julian Shun 1 © 2008–2018 by the MIT 6.172 Lecturers Binary Representation Let x = ⟨xw–1xw–2…xO⟩ be a w-bit computer word. The x unsigned integer value stored in is Ob Y The prefix M designates a Z ZM Y Mį Boolean constant. For example, the 8-bit word Ob1OO1O11O represents ం the unsigned value 15O = 2 + 4 + 16 + 128. The signed integer (two’s complement) value stored in x is sign bit Y M Y Z ZM ZY Y Mį For example, theৃ 8-ంbit wordৄ Ob1OO1O11O 1O6 2 4 16 128 represents the signed value – = + + – . 2 © 2008–2018 by the MIT 6.172 Lecturers Two’s Complement We have ObOO…O = O. What is the value of x = Ob11...1? Y M Y Z ZM ZY Mį Y ৃం M ৄY Mį Y Y ৃం ৄ Y 3 © 2008–2018 by the MIT 6.172 Lecturers Complementary Relationship Important identity Since we have x + ~x = -1, it follows that -x = ~x + 1. Example x = ObO11O11OOO ~x = Ob1OO1OO111 –x = Ob1OO1O1OOO 4 © 2008–2018 by the MIT 6.172 Lecturers Binary and Hexadecimal Decimal Hex Binary Decimal Hex Binary !! !!!! "" #!!! ## !!!# $ $ #!!# %% !!#! #! & #!#! '' !!## ## ( #!## )) !#!! #% * ##!! The prefix !1 + !#!# #' , ##!# designates a - !##! #) . ###! hex constant. / !### #+ 0 #### To translat from hex to binary, translate each hex digit to its binary equivalent, and concatenate the bits. Example: 0xDEC1DE2CODE4F00D is įįįįįįįįįįįįįįįįįįįįįįįįįįįįįįįį &'%&'%į&'(įį& 5 © 2008।।।।।।।।।।।।।।।।–2018 by the MIT 6.172 Lecturers C Bitwise Operators Operator Description & AND | OR ^ XOR (exclusive OR) ~ NOT (one’s complement) << shift left >> shift right Examples (8-bit word) A = Ob1O11OO11 B = ObO11O1OO1 A&B = ObOO1OOOO1 ~A = ObO1OO11OO A|B = Ob11111O11 A >> 3 = ObOOO1O11O A^B = Ob11O11O1O A << 2 = Ob11OO11OO 6 © 2008–2018 by the MIT 6.172 Lecturers Set the kth Bit Problem Set !th bit in a word "%to #.