DOCSLIB.ORG

Journal of the Transportation Research Forum: Volume 53, Number 3, Fall 2014

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Journal of the Transportation Research Forum: Volume 53, Number 3, Fall 2014 Volume 53, Number 3 Fall 2014 Transportation Research Forum NDSU Dept. 2880 PO Box 6050 Fargo, ND 58108-6050 www.trforum.org Journal of the Transportation Research Forum The Transportation Research Forum, founded in 1958, is an independent, nonprofit organization of transportation professionals who conduct, use, and benefit from research. Its purpose is to provide an impartial meeting ground for carriers, shippers, government officials, consultants, university researchers, suppliers, and others seeking exchange of information and ideas related to both passenger and freight transportation. More information on the Transportation Research Forum can be found on the Web at www.trforum.org. General Editors: Michael W. Babcock, Kansas State University and Kofi Obeng, North Carolina A&T State University Book Review Editor: Jack S. Ventura, Surface Transportation Board Associate Editors: Richard Gritta, University of Portland; Robert Harrison, University of Texas; Kevin H. Horn, G.E.C. Inc.; Wesley Wilson, University of Oregon; Barry Prentice, University of Manitoba; Carl Scheraga, Fairfield University; John Bitzan, North Dakota State University; and Starr McMullen, Oregon State University. Disclaimer: The facts, opinions, and conclusions set forth in the articles contained herein are those of the authors and quotations should be so attributed. They do not necessarily represent the views and opinions of the Transportation Research Forum (TRF), nor can TRF assume any responsibility for the accuracy or validity of any of the information contained herein. Memberships/Subscriptions: Subscriptions and/or membership forms may be obtained from the following office or online. Copyright 2014 The Transportation Research Forum All Rights Reserved ISSN 1046-1469 Published and Distributed by Transportation Research Forum NDSU Dept. 2880 P.O. Box 6050 Fargo, ND 58108-6050 P: (701) 231-7766 • F: (701) 231-1945 or apply online at www.trforum.org Journal of the Transportation Research Forum Volume 53, Number 3 • Fall 2014 Table of Contents A Message from the JTRF Co-General Editors 3 Kofi Obeng and Michael W. Babcock ARTICLES Optimizing Strategic Allocation of Vehicles for One-Way Car-sharing Systems Under Demand Uncertainty 7 Wei (David) Fan Measuring Performance at a Large Metropolitan Area: The Case of the DC (District of Columbia) Metroplex 21 Tony Diana Determinants of Per Capita Vehicle Miles Traveled (VMT): The Case of California 35 Mintesnot Woldeamanuel and Andrew Kent The Magnitudes of Economic and Non-Economic Factors on the Demand for U.S. Domestic Air Travel 47 Ju Dong Park and Won W. Koo Forecast of CO2 Emissions From the U.S. Transportation Sector: Estimation From a Double Exponential Smoothing Model 63 Jaesung Choi, David C. Roberts, and Eunsu Lee State Variation in Railroad Wheat Rates 83 Michael W. Babcock, Matthew McKamey, and Phillip Gayle Factors Contributing to Police Attendance at Motor Vehicle Crash Scenes 101 Richard Tay, Lina Kattan, and Yuan Bai BOOK REVIEW On the cover: Ju Dong Park and Won W. Koo identify the economic and non-economic factors that affect U.S. air travel in “The Magnitudes of Economic and Non-Economic Factors on the Demand for U.S. Domestic Air Travel.” The authors find that airfare, income, seasonality, and mergers play significant roles in the demand for airline passenger travel. 1 BOOK REVIEWS American Railroads: Decline and Renaissance in the Twentieth Century 117 Francis P. Mulvey City Distribution and Urban Freight Transport: Multiple Perspectives 121 Anthony M. Pagano Transportation Research Forum 123 Statement of Purpose 123 History and Organization 123 Annual Meetings 124 TRF Council 125 TRF Foundation Officers 125 Past Presidents 126 Recipients of the TRF Distinguished Transportation Researcher Award 126 Recipients of the Herbert O. Whitten TRF Service Award 126 Past Editors of JTRF 127 Recipients of the TRF Best Paper Award 127 Guidelines for Manuscript Submission 129 2 A Message from the JTRF Co-General Editors The fall 2014 issue of JTRF contains articles covering a broad range of topics. They are: • Optimizing Strategic Allocation of Vehicles for One-Way Car-sharing Systems Under Demand Uncertainty • Measuring Performance at a Large Metropolitan Area: The Case of the DC (District of Columbia) Metroplex • Determinants of Per Capita Vehicle Miles Traveled (VMT): The Case of California • The Magnitudes of Economic and Non-Economic Factors in the Demand for U.S. Domestic Air Travel • Forecast of C02 Emissions From the U.S. Transportation Sector: Estimation from a Double Exponential Smoothing Model • State Variation in Railroad Wheat Rates • Factors Contributing to Police Attendance at Motor Vehicle Crash Scenes. The first article is by Wei Fan and it is titled “Optimizing Strategic Allocation of Vehicles for One-way Car-sharing Systems Under Demand Uncertainty.” Fan’s focus is on making car- sharing programs sustainable. To do so he develops a multistage stochastic optimization model to study the strategic allocation of car-sharing vehicles (OSCAV) in one-way car-sharing programs. His approach, involving a multistage linear programming model, is validated using “a seven-stage experimental network” with four car-sharing locations. According to Fan the validation provides high quality solutions suggesting that his proposed models can be used in real world applications. In the second paper, Tony Diana studies the performance of the airports in Washington DC, and surrounding areas whose operations may result in conflicting arrival and departure paths. He defines such an area as a METROPLEX and uses it to answer several research questions. How is variation in block time affected by meteorological conditions? Are the influences of the variables affecting block times also affected by meteorological conditions? How do new air traffic control procedures and the capabilities of the next generation of air traffic control system (NEXTGEN) affect these airports? Are there differences in results when hierarchical linear models that account for fixed and random effects and regression models are used? The dependent variable in his models is block delay and the independent variables include en-route miles flown, average speed, the nation’s airspace system (NAS) delays, taxi-out delays, taxi-in delays, airborne delays and percent operations in instrument meteorological conditions. He concludes from his analysis that hierarchical models provide a better picture of performance, and that instrument meteorological conditions, en-route miles flown, speed, the number of NAS delays, taxi-in and taxi-out delays have significant effects on variation in block time compared to airline flight plans. The third paper is by Woldeamanuel and Kent and it is on the determinants of per capita vehicle miles traveled in California. Its aim is to identify policy variables which could help in reducing per capita vehicle miles traveled (VMT) and reduce greenhouse gas (GHG). Additionally, the paper aims to provide a better understanding of the factors which reduce VMT so that “state and regional organizations can develop effective strategies for near and long term per capita VMT and GHG reduction.” Data for the study are from the National Household Travel Survey and include information on household demographics and travel behavior. Using multivariate regression methods the authors estimate VMT equations and employ Chow’s test to reject data pooling in favor of separate models for 2001 and 2009. They find “a shift toward a more diverse group of significant 3 variables which explain and impact per capita VMT” (e.g., commuting by public transit, increasing public transit trips, bike trips), a group of variables with similar effects in the 2001 and 2009 models (e.g., distance to work, population density, travel day trips, and number of vehicles in a household) and concluded that their study supports compact urban development. Park and Koo examine “the magnitudes of economic and non-economic factors in the demand for U.S. domestic air travel” in the fourth paper with the objective of analyzing carrier behavior in capturing market share. Using a utility maximization framework they derive a demand equation whose dependent variable is airline passenger miles, and its independent variables are the fares of different airlines, disposable income, seasonality, the impact of the September 11 attack and a merger variable. This demand equation is estimated with data from the first quarter of 2000 through the third quarter of 2012 drawn from sources including airlines, the Bureau of Labor Statistics and the Economic Report of the President. They find that air fare, income, seasonality and mergers are important determinants of passenger demand. More importantly, they find that U.S. airline passenger demand is unaffected by unexpected events such as the September 11 attack on airlines. In the fifth paper Choi, Roberts and Lee write on forecasting carbon dioxide emissions in the U.S transportation sector. Their objectives are to provide forecasts of carbon dioxide at the national and state levels from 2012 to 2021 and determine if trends in carbon dioxide emissions reductions in the United States since 2000 are observable across states. Choi et al. estimate a double exponential smoothing model using data from the U.S. Environmental Protection Agency and the State Energy Data System of the U.S. Energy Information Administration to forecast carbon dioxide emissions. They find long-term trends in the reduction of carbon dioxide throughout the United States.
Load more

Recommended publications
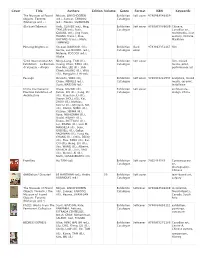
  • Booxter Export Page 1
    Cover Title Authors Edition Volume Genre Format ISBN Keywords The Museum of Found Mirjam, LINSCHOOTEN Exhibition Soft cover 9780968546819 Objects: Toronto (ed.), Sameer, FAROOQ Catalogue (Maharaja and - ) (ed.), Haema, SIVANESAN (Da bao)(Takeout) Anik, GLAUDE (ed.), Meg, Exhibition Soft cover 9780973589689 Chinese, TAYLOR (ed.), Ruth, Catalogue Canadian art, GASKILL (ed.), Jing Yuan, multimedia, 21st HUANG (trans.), Xiao, century, Ontario, OUYANG (trans.), Mark, Markham TIMMINGS Piercing Brightness Shezad, DAWOOD. (ill.), Exhibition Hard 9783863351465 film Gerrie, van NOORD. (ed.), Catalogue cover Malenie, POCOCK (ed.), Abake 52nd International Art Ming-Liang, TSAI (ill.), Exhibition Soft cover film, mixed Exhibition - La Biennale Huang-Chen, TANG (ill.), Catalogue media, print, di Venezia - Atopia Kuo Min, LEE (ill.), Shih performance art Chieh, HUANG (ill.), VIVA (ill.), Hongjohn, LIN (ed.) Passage Osvaldo, YERO (ill.), Exhibition Soft cover 9780978241995 Sculpture, mixed Charo, NEVILLE (ed.), Catalogue media, ceramic, Scott, WATSON (ed.) Installaion China International Arata, ISOZAKI (ill.), Exhibition Soft cover architecture, Practical Exhibition of Jiakun, LIU (ill.), Jiang, XU Catalogue design, China Architecture (ill.), Xiaoshan, LI (ill.), Steven, HOLL (ill.), Kai, ZHOU (ill.), Mathias, KLOTZ (ill.), Qingyun, MA (ill.), Hrvoje, NJIRIC (ill.), Kazuyo, SEJIMA (ill.), Ryue, NISHIZAWA (ill.), David, ADJAYE (ill.), Ettore, SOTTSASS (ill.), Lei, ZHANG (ill.), Luis M. MANSILLA (ill.), Sean, GODSELL (ill.), Gabor, BACHMAN (ill.), Yung
    [Show full text]
  • Miles Coolidge
    PETER BLUM GALLERY MILES COOLIDGE Born 1963 in Montreal, Quebec, Canada Lives and works in Los Angeles, CA EDUCATION 1994 Kunstakademie Düsseldorf (class of Bernd Becher), Düsseldorf, Germany 1992 MFA, California Institute of the Arts, Valencia, CA 1986 AB, Harvard University, Cambridge, MA SOLO EXHIBITIONS 2016 Coal Seam redux, Peter Blum Gallery, New York, NY Chemical Pictures, ACME., Los Angeles, CA Photographs and Chemical Pictures, Franz Josef Albers Museum Quadrat, Bochum, Germany 2015 Coal Seam redux, kunstwerden, Essen, Germany Coal Seam, Bergwerk Prosper-Haniel, NADA Art Fair, New York, NY (curated solo booth/ACME) 2014 ACME, Los Angeles Safetyville (selection), ACME, Los Angeles 2011 New Projects, ACME., Los Angeles, CA 2008 Street Furniture, ACME., Los Angeles, CA 2007 Casey Kaplan, New York, NY 2006 Juncture, ACME., Los Angeles, CA 2005 Drawbridges, Galerie Ilka Bree, Bordeaux, France Drawbridges, Galerie Lisa Ruyter, Vienna, Austria Mound Postcard Posters, Harwood Museum of Art, University of New Mexico, Taos, NM 2003 Drawbridges, ACME., Los Angeles, CA Drawbridges, Casey Kaplan Gallery, New York, NY 2002 Traffic, ACME., Los Angeles, CA Majestic Sprawl: Some Los Angeles Photography, Pasadena Museum of California Art, Pasadena, CA Observatory Circle, Galerie Gisela Capitain, Köln, Germany 2001 Miles Coolidge: Central Valley, Ulrich Museum of Art, Wichita State University, Wichita, KS ACME., Los Angeles, CA 2000 Galerie Jennifer Flay, Paris, France Orange County Museum, Newport Beach, CA Mattawa, Casey Kaplan, New York, NY 1998 Central Valley, Casey Kaplan, New York, NY Central Valley, ACME., Los Angeles, CA James Van Damme Gallery, Brussels, Belgium Moundbuilders Golf Course, ACME., Los Angeles, CA 1996 Elevator Pictures, Casey Kaplan, New York, NY Garage Pictures, ACME., Santa Monica, CA Garage Pictures, Casey Kaplan, New York, NY Safetyville, ACME., Santa Monica, CA 1994 Elevator Pictures, Los Angeles Center for Photographic Studies, Hollywood, CA 1992 In Its Place, Main Gallery, California Institute of the Arts, Valencia, CA Blumarts Inc.
    [Show full text]
  • Thomas Demand Roxana Marcoci, with a Short Story by Jeffrey Eugenides
    Thomas Demand Roxana Marcoci, with a short story by Jeffrey Eugenides Author Marcoci, Roxana Date 2005 Publisher The Museum of Modern Art ISBN 0870700804 Exhibition URL www.moma.org/calendar/exhibitions/116 The Museum of Modern Art's exhibition history— from our founding in 1929 to the present—is available online. It includes exhibition catalogues, primary documents, installation views, and an index of participating artists. MoMA © 2017 The Museum of Modern Art museumof modern art lIOJ^ArxxV^ 9 « Thomas Demand Thomas Demand Roxana Marcoci with a short story by Jeffrey Eugenides The Museum of Modern Art, New York Published in conjunction with the exhibition Thomas Demand, organized by Roxana Marcoci, Assistant Curator in the Department of Photography at The Museum of Modern Art, New York, March 4-May 30, 2005 The exhibition is supported by Ninah and Michael Lynne, and The International Council, The Contemporary Arts Council, and The Junior Associates of The Museum of Modern Art. This publication is made possible by Anna Marie and Robert F. Shapiro. Produced by the Department of Publications, The Museum of Modern Art, New York Edited by Joanne Greenspun Designed by Pascale Willi, xheight Production by Marc Sapir Printed and bound by Dr. Cantz'sche Druckerei, Ostfildern, Germany This book is typeset in Univers. The paper is 200 gsm Lumisilk. © 2005 The Museum of Modern Art, New York "Photographic Memory," © 2005 Jeffrey Eugenides Photographs by Thomas Demand, © 2005 Thomas Demand Copyright credits for certain illustrations are cited in the Photograph Credits, page 143. Library of Congress Control Number: 2004115561 ISBN: 0-87070-080-4 Published by The Museum of Modern Art, 11 West 53 Street, New York, New York 10019-5497 (www.moma.org) Distributed in the United States and Canada by D.A.P./Distributed Art Publishers, New York Distributed outside the United States and Canada by Thames & Hudson Ltd., London Front and back covers: Window (Fenster).
    [Show full text]
  • Curriculum Vitae
    Michael Ashkin www.michaelashkin.com [email protected] EDUCATION 1993 MFA, The School of the Art Institute of Chicago, Painting/Drawing, Full Merit Scholarship 1980 MA, Columbia University, New York, Middle East Languages and Cultures, Honorary President’s Fellowship, Pahlavi Foundation Scholarship 1977 BA, The University of Pennsylvania, Philadelphia, Oriental Studies, magna cum laude SOLO EXHIBITIONS 2020 “were it not for,” Kaktos Gallery, Athens, Greece, January – March 2018 “Horizont,” Bibliowicz Gallery, Cornell Unversity, Ithaca, New York, March 19– April 20 2016 “Dismal Dreaming,” Cathouse Funeral, Brooklyn, New York, March 26– May 5, and Cathouse Proper, Brooklyn, NY, April 22 – June 1 2013 “Architecture is for Creeps,” Milstein Hall Gallery, Cornell University, Ithaca, NY, March 10–April 12 2010 Johnson Museum of Art, Cornell University, Ithaca, New York, curated by Andrea Inselmann, April 3 – July 11 (artist’s book) Weatherspoon Museum of Art, Greensboro, North Carolina, January 17– April 18 2009 Secession, Vienna, Austria, curated by Annette Südbeck, November 20 – January 26, 2010 (monograph) SculptureCenter, Long Island City, New York, In Practice Projects, curated by Sarina Basta, May 10 – August 10 2005 Andrea Rosen Gallery, Gallery 2, New York, May 6– June 28 2002 Andrea Rosen Gallery, New York, November 29 – January 18, 2003 Galerie Otto Schweins, Cologne, Germany, October 30– December 21 Emily Tsingou Gallery, London, September 10 – 30 2000 Andrea Rosen Gallery, New York, January 28 – March 4 1999 Emily Tsingou Gallery,
    [Show full text]
  • Download Download
    2/20161 Science & Technology Studies ISSN 2243-4690 Co-ordinating editor Salla Sariola (University of Oxford, UK; University of Turku, Finland) Editors Torben Elgaard Jensen (Aalborg University at Copenhagen, Denmark) Sampsa Hyysalo (Aalto University, Finland) Jörg Niewöhner (Humboldt-Universität zu Berlin, Germany) Franc Mali (University of Ljubljana, Slovenia) Martina Merz (Alpen-Adria-Universität Klagenfurt, Austria) Antti Silvast (University of Edinburgh, UK) Estrid Sørensen (Ruhr-Universitat Bochum, Germany) Helen Verran (University of Melbourne, Australia) Brit Ross Winthereik (IT University of Copenhagen, Denmark) Assistant editor Louna Hakkarainen (Aalto University, Finland) Editorial board Nik Brown (University of York, UK) Miquel Domenech (Universitat Autonoma de Barcelona, Spain) Aant Elzinga (University of Gothenburg, Sweden) Steve Fuller (University of Warwick, UK) Marja Häyrinen-Alastalo (University of Helsinki, Finland) Merle Jacob (Lund University, Sweden) Jaime Jiménez (Universidad Nacional Autonoma de Mexico) Julie Thompson Klein (Wayne State University, USA) Tarja Knuuttila (University of South Carolina, USA) Shantha Liyange (University of Technology Sydney, Australia) Roy MacLeod (University of Sydney, Australia) Reijo Miettinen (University of Helsinki, Finland) Mika Nieminen (VTT Technical Research Centre of Finland, Finland) Ismael Rafols (Universitat Politècnica de València, Spain) Arie Rip (University of Twente, The Netherlands) Nils Roll-Hansen (University of Oslo, Norway) Czarina Saloma-Akpedonu (Ateneo de Manila
    [Show full text]
  • UNIVERSITY of CALIFORNIA, IRVINE Origin[Redux] Photography
    UNIVERSITY OF CALIFORNIA, IRVINE Origin[Redux] Photography as a Mechanism of Dream Transference A THESIS Submitted in partial satisfaction of the requirements for the degree of MASTER OF FINE ARTS by Joaquín Palting Thesis Committee: Professor Simon Leung, Chair Professor Jennifer Bornstein Professor Miles Coolidge Professor Gabriele Schwab 2020 © 2020 Joaquín Palting DEDICATION Dedicated to Dr. Diana Edwards and Dr. Pancracio Palting, aka Mom & Pop. “The interpretation of dreams is the royal road to a knowledge of the unconscious activities of the mind.” ~Sigmund Freud “For it is another nature that speaks to the camera rather than to the eye: “other” above all in the sense that a space informed by human consciousness gives way to a space informed by the unconscious.” ~Walter Benjamin ii TABLE OF CONTENTS Page DEDICATION ii LIST OF FIGURES iii ACKNOWLEDGEMENTS iv ABSTRACT v PREFACE 1 INTRODUCTION 2 PHOTOGRAPHY AS A MECHANISM OF DREAM TRANSFERENCE 8 CASE STUDY 13 BIBLIOGRAPHY 22 iii LIST OF FIGURES FIGURE 1 Out Taking Pictures With Mama, 1972, D.S. Edwards FIGURE 2 Untitled (Cave Interior), from the series Origin[Redux], 2020, Joaquín Palting FIGURE 3 Untitled (Dunes), 1936, Edward Weston FIGURE 4 Mendenhall Glacier, 1973, Brett Weston FIGURE 5 Untitled (Lake Reflection), 1980, D.S. Edwards FIGURE 6 Untitled (Hollywood), from the series Origin[Redux], 2020, Joaquín Palting FIGURE 7 Untitled (Flat Rock Point), from the series Origin[Redux], 2020, Joaquín Palting FIGURE 8 Untitled (Rocks), from the series Origin[Redux], 2020, Joaquín Palting FIGURE 9 Untitled (Cave Entrance), from the series Origin[Redux], 2020, Joaquín Palting FIGURE 10 Untitled (Elysian Park), from the series Origin[Redux], 2020, Joaquín Palting iv ACKNOWLEDGEMENTS I would like to express my deepest gratitude to the following people who have inspired and guided me through one of the most exciting and rewarding chapters of my life.
    [Show full text]
  • Words Without Pictures
    WORDS WITHOUT PICTURES NOVEMBER 2007– FEBRUARY 2009 Los Angeles County Museum of Art CONTENTS INTRODUCTION Charlotte Cotton, Alex Klein 1 NOVEMBER 2007 / ESSAY Qualifying Photography as Art, or, Is Photography All It Can Be? Christopher Bedford 4 NOVEMBER 2007 / DISCUSSION FORUM Charlotte Cotton, Arthur Ou, Phillip Prodger, Alex Klein, Nicholas Grider, Ken Abbott, Colin Westerbeck 12 NOVEMBER 2007 / PANEL DISCUSSION Is Photography Really Art? Arthur Ou, Michael Queenland, Mark Wyse 27 JANUARY 2008 / ESSAY Online Photographic Thinking Jason Evans 40 JANUARY 2008 / DISCUSSION FORUM Amir Zaki, Nicholas Grider, David Campany, David Weiner, Lester Pleasant, Penelope Umbrico 48 FEBRUARY 2008 / ESSAY foRm Kevin Moore 62 FEBRUARY 2008 / DISCUSSION FORUM Carter Mull, Charlotte Cotton, Alex Klein 73 MARCH 2008 / ESSAY Too Drunk to Fuck (On the Anxiety of Photography) Mark Wyse 84 MARCH 2008 / DISCUSSION FORUM Bennett Simpson, Charlie White, Ken Abbott 95 MARCH 2008 / PANEL DISCUSSION Too Early Too Late Miranda Lichtenstein, Carter Mull, Amir Zaki 103 APRIL 2008 / ESSAY Remembering and Forgetting Conceptual Art Alex Klein 120 APRIL 2008 / DISCUSSION FORUM Shannon Ebner, Phil Chang 131 APRIL 2008 / PANEL DISCUSSION Remembering and Forgetting Conceptual Art Sarah Charlesworth, John Divola, Shannon Ebner 138 MAY 2008 / ESSAY Who Cares About Books? Darius Himes 156 MAY 2008 / DISCUSSION FORUM Jason Fulford, Siri Kaur, Chris Balaschak 168 CONTENTS JUNE 2008 / ESSAY Minor Threat Charlie White 178 JUNE 2008 / DISCUSSION FORUM William E. Jones, Catherine
    [Show full text]
  • Selected Affinities
    FOR IMMEDIATE RELEASE Selected Affinities June 23 – August 31, 2018 Opening reception for the artists: Saturday, June 23, 4:00 – 6:00 pm Allan Sekula, detail from Message in a Bottle (from Fish Story Chapter 5) (first version), 1992/1994 “But it is capital that is the leading, protean force, pushing people this way and that and leaving them to stew or rot or boil over.” – Allan Sekula (1951-2013), excerpt from Fish Story Santa Monica, April 2018 — Christopher Grimes Gallery is pleased to announce its forthcoming exhibition Selected Affinities, with works by Allan Sekula, Miles Coolidge, Connie Samaras, Katie Shapiro and Billy Woodberry. From the desert to the docks, farmland to the sea, this exhibition brings together four artists, who, along with Sekula, use photography or video not only as a tool for documentation but also as part of a discourse rooted in social relations. On view for the first time at the gallery will be Sekula’s Message in a Bottle (from Fish Story Chapter 5) (first version). One of his best-known bodies of work, Fish Story is a sequential piece composed of over one hundred pictures in nine chapters documenting maritime spaces and the effects of globalization. Message in a Bottle specifically addresses the decline of the fishing economy in the small Spanish town of Vigo. Sekula has exhibited extensively both internationally and locally, with solo exhibitions most recently at Thyssen-Bornemisza Art Contemporary, Vienna, Austria; NTU Centre for Contemporary Art Singapore; and Johan Jacobs Museum, Zurich, Switzerland. His work is in the collections of the Walker Art Center, Minneapolis, MN; Museum of Modern Art New York, NY; J.
    [Show full text]
  • For Immediate Release Miles Coolidge Gallery I
    FOR IMMEDIATE RELEASE MILES COOLIDGE GALLERY I EXHIBITION DATES: JANUARY 12 – FEBRUARY 10, 2007 OPENING: THURSDAY, JANUARY 11th, 6 - 8 PM GALLERY HOURS: TUESDAY – SATURDAY, 10 - 6 PM For his fifth solo show in New York, Los Angeles-based artist, Miles Coolidge, will present two of his latest photographic projects in Gallery I. Both works recognize photography's importance in visual and popular culture, embracing the medium as a conceptual and surrealist tool in the history of art. Coolidge works between traditional photographic genres and strategies, de-familiarizing our accustomed approach to our surroundings. His most ambitious project to date, Wall of Death, is an installation of 20 color photographs that replicates a complete and full-scale representation of the performing surface of the traveling carnival act, “Don Daniel's Wall of Death Motorcycle Thrill Show,” operated by the California Hellriders, who are based in Swansea, Massachusetts. Each photograph corresponds to one of the Wall of Death's wooden panels, and the images are mounted edge-to edge on the gallery wall, echoing how the structure appears when fully assembled. Coolidge shot the images on the grounds of the Iron Horse Saloon, Ormond Beach, Florida, during “Biketoberfest 2006”. The Wall of Death is a vertical wooden cylinder in which trained motorcycle and go-kart riders perform for audiences. The riders are held to the sheer surface by the centripetal force generated by their velocities of 35 mph or more. Coolidge’s 20 images depict the 7' wooden surface on which the riders perform. Currently there are 3 Walls of Death in operation in the United States that travel between motorcycling events in the South, the Midwest and the Northeast, in addition to others based in Great Britain, Europe and perhaps elsewhere.
    [Show full text]
  • Jan | Feb | March | 2016
    jan | feb | march | 2016 s a n t a b a r b a r a m u s e u m o f a r t from the director Dear Members, This new year is especially significant as it marks an important milestone—the Museum’s 75th anniversary. On Thursday, June 5, 1941, the Santa Barbara Museum of Art opened its doors for the first time amidst a throng of community leaders, local schoolchildren, and SBMA founders. The idea for a city museum originally came from the local artist Colin Campbell Cooper. When he learned that the main post office building, erected in 1912 and abandoned for several years, was going to be sold, he proposed, in a letter published in the Santa Barbara News-Press in July of 1937, that the impressive Italianate structure should be transformed into a museum. What Cooper himself described as something of a “pipedream” came to fruition just four years later, thanks to a groundswell of support from the community and the commitment of a small, passionate army of artists and civic-minded individuals. Also voicing their enthusiasm for the project was a large group of merchants, some 125 of whom petitioned the County’s Board of Supervisors to buy the property from the federal government so that it may be used as a museum. Their plea was heeded and, before long, a number of Santa Barbara residents formed an official museum committee and a number of generous citizens offered funds to remodel the building, to construct galleries, and to add new floors and lighting that would be up to museum standards.
    [Show full text]
  • Yunhee Min CV
    YUNHEE MIN received her Bachelor of Fine Arts degree from the Art Center College of Design in Pasadena, CA in 1991 and her Master of Arts from Harvard University, Graduate School of Design in 2008, with additional studies in 1994 at Kunstakademie in Düsseldorf, Germany. Min has had numerous solo exhibitions both nationally and internationally, which include “Hammer Projects: Yunhee Min,” Hammer Museum, Los Angeles, CA; “Wilde Paintings,” “movements,” and “Into the Sun,” Susanne Vielmetter Los Angeles Projects, Culver City, CA; “For Instance,” Hammer Museum, Los Angeles, CA; “Above and Beyond,” Pasadena Museum of Contemporary Art, CA; “Distance is like the future, Circa Series,” Museum of Contemporary Art San Diego, CA; “Fading Wild,” Finesilver Gallery, San Antonio, TX; “One foot in front of the other,” Or Gallery, Vancouver, Canada; “Fast times,” ACME., Los Angeles, CA; among others. Recent group exhibitions include “The Light Touch,” Vielmetter Los Angeles, Los Angeles, CA; “Belief in Giants,” Miles McEnery Gallery, New York, NY; “Elemental | Seeing the Light,” Stuart Haaga Gallery, Descanso Gardens, Los Angeles, CA; “Spectra,” San Diego State University Downtown Gallery, San Diego, CA; “Lost line,” Los Angeles County Museum of Art, Los Angeles, CA; “ABCyz,” Launch Exhibition, Silvershed, New York, NY; “The Trans-Aestheticization of Daily Life,” University of California, Riverside Sweeney Gallery, Riverside, CA; “Too much love,” Angles Gallery, Los Angeles, CA, curated by Amy Adler; “Around About Abstraction,” Weatherspoon Art Museum, Greensboro, NC; “Wall Painting,” University of Texas at San Antonio, San Antonio, TX; “Snap Shot,” UCLA Hammer Museum, Los Angeles, CA (traveled to Museum of Contemporary Art, North Miami, FL); “Fresh,” Altoids Curiously Strong Collection, New Museum, New York, NY; “KOREAMERICAKOREA,” Sonje Museum of Contemporary Art, Seoul, Korea; “Rundgang,” Kunstakademie Düsseldorf, Düsseldorf, Germany.
    [Show full text]
  • April Friges CV 2021 Work
    AprilFriges.com / 330.760.5409 / [email protected] APRIL DAWN FRIGES Education 2007-2010 University of California, Irvine, Irvine, California, U.S.A. MFA, Studio Art 2000-2004 University of Akron, Akron, Ohio, U.S.A. BFA, Photography, Cum Laude Minors, Professional Photography & Computer Imaging Qualifications Large Format Photography Medium Format & 35mm Analog Photography Medium Format Digital + 35mm Digital SLR Color Darkroom, Advanced Black and White & Film Developing Experimental Black and White + Color Photography Techniques (camera + darkroom) Digital Negatives Adobe Photoshop 2021-5.5 Adobe Lightroom 10.1-1.0 including standardizing Custom Metadata + Copyright + Batch Processing Camera Raw 6.0, Adobe Bridge 2021 & Acrobat Pro DC i1 Professional Color Management (i1 Photo Pro 3 - 1) for custom paper, printer + monitor calibration Drum Scanning: Howtek 7500 + Flextight (virtual) Piezo Printing Setup for Epson Professional Printers Wet-Mount Negative Scanning Large Scale Digital Printing: Epson 11880, 9890 Large Scale Color Darkroom & Maintenance: 54” Kreonite KM4 Color Processor Color Balancing & Printing in a Professional Wet-Lab Alternative Darkroom Processes: Tintype/Wet Plate, Photogravure, Platinum Printing, Cyanotype, Van Dyke Professional Studio Lighting: strobes and hot lights - Profoto Adobe Illustrator CC-CS Adobe Premier, Final Cut Pro, After Effects and DVD Studio Pro 16mm Motion Film: exposing, grading + splicing Filemaker Pro - art studio management organization / solutions Teaching across Mac & Windows Operating Systems
    [Show full text]