Characterization of the Distribution of Participation in Wikis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Beets Documentation Release 1.5.1
beets Documentation Release 1.5.1 Adrian Sampson Oct 01, 2021 Contents 1 Contents 3 1.1 Guides..................................................3 1.2 Reference................................................. 14 1.3 Plugins.................................................. 44 1.4 FAQ.................................................... 120 1.5 Contributing............................................... 125 1.6 For Developers.............................................. 130 1.7 Changelog................................................ 145 Index 213 i ii beets Documentation, Release 1.5.1 Welcome to the documentation for beets, the media library management system for obsessive music geeks. If you’re new to beets, begin with the Getting Started guide. That guide walks you through installing beets, setting it up how you like it, and starting to build your music library. Then you can get a more detailed look at beets’ features in the Command-Line Interface and Configuration references. You might also be interested in exploring the plugins. If you still need help, your can drop by the #beets IRC channel on Libera.Chat, drop by the discussion board, send email to the mailing list, or file a bug in the issue tracker. Please let us know where you think this documentation can be improved. Contents 1 beets Documentation, Release 1.5.1 2 Contents CHAPTER 1 Contents 1.1 Guides This section contains a couple of walkthroughs that will help you get familiar with beets. If you’re new to beets, you’ll want to begin with the Getting Started guide. 1.1.1 Getting Started Welcome to beets! This guide will help you begin using it to make your music collection better. Installing You will need Python. Beets works on Python 3.6 or later. • macOS 11 (Big Sur) includes Python 3.8 out of the box. -

SOCIAL MEDIA MAP 2013 a Snapshot of the Evolving Landscape
SOCIAL MEDIA MAP 2013 A Snapshot of the Evolving Landscape Social Networks Podcasting Photo Sharing Social Commerce Video Sharing URL Shorteners facebook itunes podcasts pinterest eversave youtube tinyurl google plus librivox picasa groupon vimeo bitly path podbean tinypic google offers dailymotion goo.gl meet-up snapchat saveology vevo ow.ly tagged International Social photobucket scoutmob vox is.gd gather Networks pingram livingsocial qik snipurl bu.mp vk pheed plumdistrict telly badoo smile polyvore blip.tv E-Commerce Platforms Professional Social odnoklassniki.ru flickr yipit videolla shopify Networks skyrock kaptur vine volusion linkedin sina weibo fotolog Social Gaming ptch ecwid scribd wretch.cc imgur zynga nexternal docstoc qzone instagram the sims social graphite issuu studivz fotki habbo Social Q&A wanelo plaxo 51 second life quora etsy telligent iwiw.hu xbox live Private Social Networks answers fancy slideshare hyves.nl smallworlds ning stack exchange gilt city xing migente battle net yammer yahoo answers doximity cyworld playstation network hall wiki answers naymz cloob imvu convo allexperts Websites gaggleamp mixi.jp salesforce chatter gosoapbox viadeo renren Product/Company Reviews glassboard answerbag Mobile Apps doc2doc yelp swabr ask.com Microblogging angie's list spring.me Social Recruiting communispace Tools & Platforms twitter bizrate blurtit indeed tumblr buzzilions fluther freelancer disqus epinions glassdoor plurk Social Bookmarking consumersearch SHARE THE MAP elance storify & Sharing insiderpages Wikis odesk digg -

Quick Guide to the Web
Quick Guide to the Web For Reference & For Fun Reference General Reference Wiki Reference Academic Encyclopedias Dictionaries More Glossaries by Topic Basic Info Phone & Address Maps & Directions News Weather Health Answers & How-To Basic Sites Internet Basics News News & Politics Newspapers Media Research Entertainment Movies & TV Shows/Movies Online Movies Television Reference Pop Culture Music Online Music Music Sites Reference Games Computer & Console Internet Puzzles & More Media & Fun Online Video Humor/Fun Baseball & Other Sports Government General Depts & Agencies Law Public_Resources Data & Statistics Travel General Flights Driving Automobiles Hotels Studying Academic Study Aids General Reference Data & Statistics Wiki Reference Encyclopedias Dictionaries More Glossaries by Topic Media Online Shows & Movies Music Video Internet Games Books Newspapers Magazines More Local Info Genealogy Finding Basic Information Basic Search & More Google Yahoo Bing MSN ask.com AOL Wikipedia About.com Internet Public Library Freebase Librarian Chick DMOZ Open Directory Executive Library Web Research OEDB LexisNexis Wayback Machine Norton Site-Checker DigitalResearchTools Web Rankings Alexa Web Tools - Librarian Chick Web 2.0 Tools Top Reference & Resources – Internet Quick Links E-map | Indispensable Links | All My Faves | Joongel | Hotsheet | Quick.as Corsinet | Refdesk Tools | CEO Express Internet Resources Wayback Machine | Alexa | Web Rankings | Norton Site-Checker Useful Web Tools DigitalResearchTools | FOSS Wiki | Librarian Chick | Virtual -

Making Metadata: the Case of Musicbrainz
Making Metadata: The Case of MusicBrainz Jess Hemerly [email protected] May 5, 2011 Master of Information Management and Systems: Final Project School of Information University of California, Berkeley Berkeley, CA 94720 Making Metadata: The Case of MusicBrainz Jess Hemerly School of Information University of California, Berkeley Berkeley, CA 94720 [email protected] Summary......................................................................................................................................... 1! I.! Introduction .............................................................................................................................. 2! II.! Background ............................................................................................................................. 4! A.! The Problem of Music Metadata......................................................................................... 4! B.! Why MusicBrainz?.............................................................................................................. 8! C.! Collective Action and Constructed Cultural Commons.................................................... 10! III.! Methodology........................................................................................................................ 14! A.! Quantitative Methods........................................................................................................ 14! Survey Design and Implementation..................................................................................... -

Wikis for Dummies‰
01_043998 ffirs.qxp 6/19/07 8:20 PM Page i Wikis FOR DUMmIES‰ by Dan Woods and Peter Thoeny Foreword by Ward Cunningham Inventor of wikis 01_043998 ffirs.qxp 6/19/07 8:20 PM Page ii Wikis For Dummies® Published by Wiley Publishing, Inc. 111 River Street Hoboken, NJ 07030-5774 www.wiley.com Copyright © 2007 by Wiley Publishing, Inc., Indianapolis, Indiana Published by Wiley Publishing, Inc., Indianapolis, Indiana Published simultaneously in Canada No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permit- ted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600. Requests to the Publisher for permission should be addressed to the Legal Department, Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indianapolis, IN 46256, (317) 572-3447, fax (317) 572-4355, or online at http:// www.wiley.com/go/permissions. Trademarks: Wiley, the Wiley Publishing logo, For Dummies, the Dummies Man logo, A Reference for the Rest of Us!, The Dummies Way, Dummies Daily, The Fun and Easy Way, Dummies.com, and related trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates in the United States and other countries, and may not be used without written permission. All other trademarks are the property of their respective owners. -
List of Internet Encyclopedias
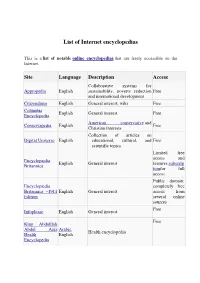
List of Internet encyclopedias This is a list of notable online encyclopedias that are freely accessible on the Internet. Site Language Description Access Collaborative systems for Appropedia English sustainability, poverty reduction Free and international development Citizendium English General interest, wiki Free Columbia English General interest Free Encyclopedia American conservative and Conservapedia English Free Christian interests Collection of articles on Digital Universe English educational, cultural, and Free scientific topics Limited free access and Encyclopædia English General interest features, subscrip Britannica tion for full access Public domain: Encyclopædia completely free Britannica –1911 English General interest access from Edition several online sources Free Infoplease English General interest Free King Abdulllah Abdul Aziz Arabic , Health encyclopedia Health English Encyclopedia Site Language Description Access General interest - Affiliated with Unification Church; in part, New World English selects and rewrites certain Free Encyclopedia Wikipedia articles to reflect Unification Church values. Probert English General interest Free Encyclopaedia Articles are written by scholars Scholarpedia English Free and peer-reviewed for accuracy Biography Site Language Description Access The original 19th century version of the above. Available Dictionary of English free in a variety of places, either Free (see left) National Biography as transcriptions or images of the printed volumes MacTutor History of English Biographies of mathematicians Free Mathematics archive A wiki encyclopedia that allows MyWikiBiz English people and enterprises to write Free about themselves Antiquities, arts, and literature Site Language Description Access A Dictionary of Incorporates text from the 19th Greek and Roman English century encyclopedia of the same Free Antiquities name. Focuses on topics of cultural Site Language Description Access and historical Greek and Roman significance. -

Wikipedia and Wikis Haider, Jutta
Wikipedia and Wikis Haider, Jutta; Sundin, Olof Published in: The Handbook of Peer Production DOI: 10.1002/9781119537151.ch13 2021 Document Version: Peer reviewed version (aka post-print) Link to publication Citation for published version (APA): Haider, J., & Sundin, O. (2021). Wikipedia and Wikis. In M. O'Neil, C. Pentzold, & S. Toupin (Eds.), The Handbook of Peer Production (pp. 169-184). (Wiley Handbooks in Communication and Media Series ). Wiley. https://doi.org/10.1002/9781119537151.ch13 Total number of authors: 2 Creative Commons License: CC BY-NC-ND General rights Unless other specific re-use rights are stated the following general rights apply: Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal Read more about Creative commons licenses: https://creativecommons.org/licenses/ Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. LUND UNIVERSITY PO Box 117 221 00 Lund +46 46-222 00 00 This is the author’s version of a chapter accepted for publication in the Handbook of Peer Production. -

The Handbook of Peer Production Chapter 13: Wikipedia and Wikis
This is the author’s version of a chapter accepted for publication in the Handbook of Peer Production. Changes resulting from the publishing process such as copy-editing, typesetting, and other quality control mechanisms may not be reflected in this document. This author manuscript version is available for personal, non-commercial and no derivative uses only. Citation: Haider, J. & Sundin, O. (2021). Wikipedia and wikis. In: M. O’Neil, C. Pentzold & S. Toupin (Eds.), The Handbook of Peer Production (pp. 169-184). Malden, MA: Wiley-Blackwell. ISBN 9781119537106 Available at: https://www.wiley.com/en-au/The+Handbook+of+Peer+Production-p-9781119537090 The Handbook of Peer Production Chapter 13: Wikipedia and Wikis Jutta Haider, University of Borås, Sweden & Olof Sundin, Lund University, Sweden Chapter 13 – Wikis and Wikipedia 2 1. Introduction WikiWikiWebs or wikis constitute the core platform of peer production. Wikis are software programs allowing for flexible collaboration without necessarily having a defined content owner or leader. A wiki is a user-editable website or content management system. Wikis might use different programming languages and licenses, but they apply the same model for cooperation, which means that collaborators can modify content, insert hyperlinks, and change the structure of a document directly in any web browser. Edits are usually archived and open to revision for all collaborators. The most popular and successful wiki-based project by far is Wikipedia. Established in 2001, today this encyclopedia is one of the most popular sites on the Web; what is more, with its data supporting other applications and commercial platforms like Google, Wikipedia has taken on an infrastructural role in the contemporary internet. -

Automatic Music Classification with Jmir
Automatic Music Classification with jMIR Cory McKay Music Technology Area Department of Music Research Schulich School of Music McGill University, Montreal Submitted January 2010 A thesis submitted to McGill University in partial fulfillment of the requirements of the degree of Doctor of Philosophy. © Cory McKay 2010 2 Abstract Automatic music classification is a wide-ranging and multidisciplinary area of inquiry that offers significant benefits from both academic and commercial perspectives. This dissertation focuses on the development of jMIR, a suite of powerful, flexible, accessible and original software tools that can be used to design, share and apply a wide range of automatic music classification technologies. jMIR permits users to extract meaningful information from audio recordings, symbolic musical representations and cultural information available on the Internet; to use machine learning technologies to automatically build classification models; to automatically collect profiling statistics and detect metadata errors in musical collections; to perform experiments on large, stylistically diverse and well-labelled collections of music in both audio and symbolic formats; and to store and distribute information that is essential to automatic music classification in expressive and flexible standardised file formats. In order to have as diverse a range of applications as possible, care was taken to avoid tying jMIR to any particular types of music classification. Rather, it is designed to be a general-purpose toolkit that can be applied to arbitrary types of music classification. Each of the jMIR components is also designed to be accessible not only by users with a high degree of expertise in computer-based research technologies, but also by researchers with valuable musical expertise, but perhaps less of a background in computational research. -

World Wide Web 18 Web 2.0 24 Wikipedia 27
Teoria e Tecnica dei Nuovi Media - Prof.Pescatore a/a 2010-2011 PDF generato attraverso il toolkit opensource ''mwlib''. Per maggiori informazioni, vedi [[http://code.pediapress.com/ http://code.pediapress.com/]]. PDF generated at: Wed, 03 Nov 2010 19:55:26 UTC Indice Voci Storia 1 ARPANET 1 Internet 2 Digitalizzazione 10 World Wide Web 18 Web 2.0 24 Wikipedia 27 Cultura 43 Multimedialità 43 Ipertesto 44 Convergenza (multimedialità) 47 Intelligenza collettiva 48 Social media 52 Contenuto generato dagli utenti 56 Comunità virtuale 58 Wiki 62 Realtà aumentata 70 Alternate reality game 72 Open source 73 Software libero 79 Tecnologia 86 Portale:Informatica/Telematica 86 Protocollo di rete 92 Suite di protocolli Internet 96 Indirizzo IP 98 File Transfer Protocol 102 Hypertext Transfer Protocol 106 Uniform Resource Locator 110 Browser 111 File sharing 116 Peer-to-peer 124 IPTV 135 Web TV 138 Streaming 140 Forum (Internet) 142 Note Fonti e autori delle voci 145 Fonti, licenze e autori delle immagini 147 Licenze della voce Licenza 149 1 Storia ARPANET ARPANET (acronimo di "Advanced Research Projects Agency NETwork", in italiano "rete dell'agenzia dei progetti di ricerca avanzata"), anche scritto ARPAnet o Arpanet, venne studiata e realizzata nel 1969 dal DARPA, l'agenzia del Dipartimento della Difesa degli Stati Uniti responsabile per lo sviluppo di nuove tecnologie ad uso militare. Si tratta della forma per così dire embrionale dalla quale poi nel 1983 nascerà Internet. Arpanet fu pensata per scopi militari statunitensi durante la Guerra Fredda, ma paradossalmente ne nascerà uno dei più grandi progetti civili: una rete globale che collegherà tutta la Terra. -

Copyrighted Material
27_043998 bindex.qxp 6/19/07 8:31 PM Page 303 Index potential size of wiki, 196 • Symbols • security level, 195 * (asterisk) in wiki markup, 41, 118 skill level of users, 194 %ATTACHURL% TWiki variable, 145 system requirements, 215–217 %ATTACHURLPATH% TWiki variable, 50 technical expertise, 197 - (dashes) in wiki markup, 40–41, 120–121 for walkabout examples, 203 $ (dollar sign) for variable parameters, 256 yourself as wiki champion, 197 %DRAWING% TWiki variable, 278 asterisk (*) in wiki markup, 41, 118 ! (exclamation mark) preventing links, 134 Atkinson, Bill (HyperCard creator), 24–25 % (percent signs) enclosing variables, 255 Atlassian’s Confluence wiki, 29, 139, 198 + (plus sign) for wiki markup heading attaching files to pages levels, 40–41, 120–121 linking to attachments, 144–145 ? (question mark) uploading attachments, 142–144 creating page by clicking, 45–46, 136 as wiki engine feature, 16 for links to pages not yet existing, 45, 136 wiki engine variations for, 141 %SEARCH% variable (TWiki), 259–260 %ATTACHURL% TWiki variable, 145 [ ] (square brackets) %ATTACHURLPATH% TWiki variable, 50 for categories in MediaWiki, 148 attitudes, wiki, 283–286 double, for free linking, 134–135, 140–141 attracting users double, for Wikipedia internal links, 88–89 advertising, 186 single, for Wikipedia named links, 90 assisting the wiki, 186–187 for WikiSpaces links, 110 challenges for, 179 | (vertical bar or pipe) in wiki markup, collaboration, promoting, 184–185 122–123, 135 to community wikis, 185–187 confusing your audience, avoiding, 180 controversy, avoiding, 182 • A • educating users, 181, 184 elevator pitch for, 179 access control, 27, 249–250 encouraging boldness, 185 ActionTrackerPlugin, 279 Field of Dreams syndrome, avoiding, 181 administrator role, 23, 225, 228, 289 focusing the wiki, 186 advertising on wikis, 115–116 COPYRIGHTEDinstigating MATERIAL use, 184 advocacy wikis, 70–72 neglecting your wiki, avoiding, 180–181 alphabetical taxonomy, 155 to office wikis, 187–188 Apache server, 217 overdesigning, avoiding, 182 application wikis, 29, 30. -

Analýza Konceptu Web 2.0 a Návrh Využití Jeho Technologií a Služeb V Knihovně
MASARYKOVA UNIVERZITA FILOZOFICKÁ FAKULTA Ústav české literatury a knihovnictví Kabinet informačních studií a knihovnictví Analýza konceptu web 2.0 a návrh využití jeho technologií a služeb v knihovně Magisterská diplomová práce Autor práce: Bc. Jan Kamenický Vedoucí práce: PhDr. Petr Škyřík Brno 2008 Bibliografický záznam KAMENICKÝ, Jan. Analýza konceptu web 2.0 a návrh využití jeho technologií a služeb v knihovně. Brno: Masarykova univerzita, Filozofická fakulta, Ústav čes- ké literatury a knihovnictví, Kabinet informačních studií a knihovnictví, 2008. 117 s. + 7 s. příloh. Vedoucí diplomové práce PhDr. Petr Škyřík. Anotace Magisterská práce „Analýza konceptu web 2.0 a návrh využití jeho technologií a služeb v knihovně“ se zabývá konceptem web 2.0, jedním z nejdiskutovanějších internetových fenoménů současnosti. Web 2.0 je označení pro nové webové služby, marketingové strategie a způsoby využívání dat, které se objevily po krachu tzv. internetové bubliny. Nejdůležitější změnou je pak zapojení uživatelů do tvorby obsahu webu a vznik online komunit. Práce se pokouší o formulaci definice a co nejkomplexnější představení tohoto konceptu. Ukazuje hlavní aspekty a principy webu 2.0 (long tail, využití kolektivní inteligence, síťový efekt), seznamuje čtenáře s jeho charakteristickými technologiemi (AJAX, RSS, podcasting, sociální záložkování, tagy, wiki, blogy), kategorizuje a popisuje jeho typické aplikace (Del.icio.us, YouTube, Flickr, Amazon, Wikipedie, MySpace a daší). Nastiňuje i sociální aspekty používání webu 2.0. Práce rovněž představuje související koncept knihovna 2.0, který se pokouší aplikovat poznatky z webu 2.0 v prostředí knihovny a vrátit jí tak její respektované postavení v informačním procesu. Praktická část představuje návrh možného rozšíření stávajících služeb Studijní a vědecké knihovny v Hradci Králové pomocí technologií (blog, RSS, podcasting) a služeb (fotoalbum, záložky, mapy) webu 2.0.