DOCSLIB.ORG

CONFIDENCE Vs PREDICTION INTERVALS 12/2/04 Inference for Coefficients Mean Response at X Vs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CONFIDENCE Vs PREDICTION INTERVALS 12/2/04 Inference for Coefficients Mean Response at X Vs STAT 141 REGRESSION: CONFIDENCE vs PREDICTION INTERVALS 12/2/04 Inference for coefficients Mean response at x vs. New observation at x Linear Model (or Simple Linear Regression) for the population. (“Simple” means single explanatory variable, in fact we can easily add more variables ) – explanatory variable (independent var / predictor) – response (dependent var) Probability model for linear regression: 2 i ∼ N(0, σ ) independent deviations Yi = α + βxi + i, α + βxi mean response at x = xi 2 Goals: unbiased estimates of the three parameters (α, β, σ ) tests for null hypotheses: α = α0 or β = β0 C.I.’s for α, β or to predictE(Y |X = x0). (A model is our ‘stereotype’ – a simplification for summarizing the variation in data) For example if we simulate data from a temperature model of the form: 1 Y = 65 + x + , x = 1, 2,..., 30 i 3 i i i Model is exactly true, by construction An equivalent statement of the LM model: Assume xi fixed, Yi independent, and 2 Yi|xi ∼ N(µy|xi , σ ), µy|xi = α + βxi, population regression line Remark: Suppose that (Xi,Yi) are a random sample from a bivariate normal distribution with means 2 2 (µX , µY ), variances σX , σY and correlation ρ. Suppose that we condition on the observed values X = xi. Then the data (xi, yi) satisfy the LM model. Indeed, we saw last time that Y |x ∼ N(µ , σ2 ), with i y|xi y|xi 2 2 2 µy|xi = α + βxi, σY |X = (1 − ρ )σY Example: Galton’s fathers and sons: µy|x = 35 + 0.5x ; σ = 2.34 (in inches). For comparison: σY = 2.7. Note: σ is SD of y given x. It is less than the unconditional SD of Y , σY (without x fixed). e.g. consider extreme case when y = x: σ=0, but σY = σX . Estimating parameters (α, β, σ2) from a sample P 2 Recall the least squares estimates: (a,b) chosen to minimize (yi − a − bxi) : P sy (xi − x¯)(yi − y¯) a =y ¯ − bx¯ b = r = P 2 sx (xi − x¯) Fitted values: yˆ = a + bxi Residuals: ei = yi − yˆi = yi − a − bxi = α + βxi + i − a − bxi = (α − a) + (β − b)xi + i e = deviations in sample, where i i = deviations in model Estimate of σ2: Again, use the squared scale: 2 1 X 2 1 X 2 q 2 sY |x = ei = (yi − a − bxi)i , s = sY |x (n − 2) = “degrees of freedom” n − 2 i n − 2 i Why n-2?? 1 2 2 1 P 2 1. Recall with SRS Yi ∼ N(µ, σ ), s = n−1 (yi − y¯) (and y¯ estimates µ – we estimate one parameter) Here, two parameter estimates: a estimates α , and b estimates β. 2. There are two linear constraints on ei: • e¯ =y ¯ − a − bx¯ =y ¯ − (¯y − bx¯) − bx¯ = 0 P • (xi − x¯)ei = 0 2 2 Properties of Regression Estimates. Assume model (LM ): then (a, b, s = sY |x) are random variables. 2 2 2 1. Means (a, b, s = sY |x) are unbiased estimates of (α, β, σ ) 2. Variances For (a, b) variances are ( 2 ) 2 2 2 1 x¯ 2 σ σa = V ar(a) = σ + P 2 , σb = V ar(b) = P 2 n (xi − x¯) (xi − x¯) 3. (a, b) are jointly normal – in particular s2 a ∼ N(α, σ2), b ∼ N(β, σ2), (n − 2) ∼ χ2 (and a,b, and s2 are independent). a b σ2 n−2 Confidence Intervals: at level α CI’s always have the form: Est ± t α SE 1− 2 ,(n−2) Est SEEstmeans σEst with σ replaced by its estimate s. Thus v u 2 s u 1 x¯ SEb = q , SEa = st + P 2 n P(x − x¯)2 (xi − x¯) i slope b ± t1− α ,(n−2)SEb Thus, (1 − α)% CI for: 2 intercept a ± t α SE 1− 2 ,(n−2) a Tests Described here for slope β , ( but same for intercept α). b−β0 For H0 : β = β0, use t = which under H0 has the tn−2 distribution. SEb P values: One sided: (e.g.) H1 : β < β0, P = P (tn−2 < tobs) Two sided: H1 : β 6= β0, P = 2P (tn−2 > |tobs|) ( Aside: Why tn−2? t ∼ N(0,1) By definition ν q 2 , with numerator and denominator variable independent. But we can write the χν ν slope test statistic in the form (b − β )/σ t = 0 b r 2 SEb 2 σb and now we can note from properties (1) – (3) that 2 2 2 2 2 (b − β0)/σb ∼ N(0, 1) and SEb /σb = s /σ ∼ χn−2 2 and it can be shown that b and s are independent. This shows that the test statistic t ∼ tn−2.) 2 Vs New Observation at x Mean response at x new ∗ ∗ new ∗ Want to predict y (x ) = α + βx + Want to estimate µY |x∗ = α + βx ∗ ∗ new draw of y from subpopulation given x = x mean for subpopulation given x = x ∗ ∗ ∗ Point prediction:yˆ(x ) = a + bx Point estimate:µˆ ∗ = a + bx Y |x Sources of uncertainty :a, b estimated. Sources of uncertainty :a, b estimated. random error of new observ. v u 1 (x∗ − x¯)2 2 2 2 u SE ∗ = s + SE SE = st + yˆ(x ) Y |x µˆY |x∗ µˆY |x∗ P 2 n (xi − x¯) Prediction Interval : level (1 − α)% n-2 df CI :level (1 − α)% n-2 df ∗ yˆ(x ) ± t1−α/2,n−2SEyˆ(x∗) ∗ µˆY |x ± t1−α/2,n−2SEµˆY |x∗ Claim: 95% of the time , Pred. Interv. covers Claim: 95% of the time , CI covers new ∗ ∗ y (x ) µ ∗ = α + βx Y |x ie ie new yˆ − t1−α/2,n−2SE ≤ y ≤ yˆ + t1−α/2,n−2SE µˆ − t1−α/2,n−2SEµˆ ≤ µ ≤ µˆ + t1−α/2,n−2SEµˆ predict(lm(y ~ x), data, > predict(lm(y ~ x), new, interval="prediction",se.fit=T) interval="confidence",se.fit=T) $fit $fit fit lwr upr fit lwr upr 1 -1.827565 -3.99873 0.34360 1 -1.82756 -3.165220 -0.48991 2 -1.558351 -3.60936 0.49266 2 -1.55835 -2.690602 -0.42610 3 -1.289137 -3.23751 0.65924 3 -1.28914 -2.222694 -0.35558 4 -1.019922 -2.88608 0.84624 4 -1.01992 -1.766869 -0.27298 3.
Load more

Recommended publications
  • Choosing a Coverage Probability for Prediction Intervals
    Choosing a Coverage Probability for Prediction Intervals Joshua LANDON and Nozer D. SINGPURWALLA We start by noting that inherent to the above techniques is an underlying distribution (or error) theory, whose net effect Coverage probabilities for prediction intervals are germane to is to produce predictions with an uncertainty bound; the nor- filtering, forecasting, previsions, regression, and time series mal (Gaussian) distribution is typical. An exception is Gard- analysis. It is a common practice to choose the coverage proba- ner (1988), who used a Chebychev inequality in lieu of a spe- bilities for such intervals by convention or by astute judgment. cific distribution. The result was a prediction interval whose We argue here that coverage probabilities can be chosen by de- width depends on a coverage probability; see, for example, Box cision theoretic considerations. But to do so, we need to spec- and Jenkins (1976, p. 254), or Chatfield (1993). It has been a ify meaningful utility functions. Some stylized choices of such common practice to specify coverage probabilities by conven- functions are given, and a prototype approach is presented. tion, the 90%, the 95%, and the 99% being typical choices. In- deed Granger (1996) stated that academic writers concentrate KEY WORDS: Confidence intervals; Decision making; Filter- almost exclusively on 95% intervals, whereas practical fore- ing; Forecasting; Previsions; Time series; Utilities. casters seem to prefer 50% intervals. The larger the coverage probability, the wider the prediction interval, and vice versa. But wide prediction intervals tend to be of little value [see Granger (1996), who claimed 95% prediction intervals to be “embarass- 1.
    [Show full text]
  • STATS 305 Notes1
    STATS 305 Notes1 Art Owen2 Autumn 2013 1The class notes were beautifully scribed by Eric Min. He has kindly allowed his notes to be placed online for stat 305 students. Reading these at leasure, you will spot a few errors and omissions due to the hurried nature of scribing and probably my handwriting too. Reading them ahead of class will help you understand the material as the class proceeds. 2Department of Statistics, Stanford University. 0.0: Chapter 0: 2 Contents 1 Overview 9 1.1 The Math of Applied Statistics . .9 1.2 The Linear Model . .9 1.2.1 Other Extensions . 10 1.3 Linearity . 10 1.4 Beyond Simple Linearity . 11 1.4.1 Polynomial Regression . 12 1.4.2 Two Groups . 12 1.4.3 k Groups . 13 1.4.4 Different Slopes . 13 1.4.5 Two-Phase Regression . 14 1.4.6 Periodic Functions . 14 1.4.7 Haar Wavelets . 15 1.4.8 Multiphase Regression . 15 1.5 Concluding Remarks . 16 2 Setting Up the Linear Model 17 2.1 Linear Model Notation . 17 2.2 Two Potential Models . 18 2.2.1 Regression Model . 18 2.2.2 Correlation Model . 18 2.3 TheLinear Model . 18 2.4 Math Review . 19 2.4.1 Quadratic Forms . 20 3 The Normal Distribution 23 3.1 Friends of N (0; 1)...................................... 23 3.1.1 χ2 .......................................... 23 3.1.2 t-distribution . 23 3.1.3 F -distribution . 24 3.2 The Multivariate Normal . 24 3.2.1 Linear Transformations . 25 3.2.2 Normal Quadratic Forms .
    [Show full text]
  • Inference in Normal Regression Model
    Inference in Normal Regression Model Dr. Frank Wood Remember I We know that the point estimator of b1 is P(X − X¯ )(Y − Y¯ ) b = i i 1 P 2 (Xi − X¯ ) I Last class we derived the sampling distribution of b1, it being 2 N(β1; Var(b1))(when σ known) with σ2 Var(b ) = σ2fb g = 1 1 P 2 (Xi − X¯ ) I And we suggested that an estimate of Var(b1) could be arrived at by substituting the MSE for σ2 when σ2 is unknown. MSE SSE s2fb g = = n−2 1 P 2 P 2 (Xi − X¯ ) (Xi − X¯ ) Sampling Distribution of (b1 − β1)=sfb1g I Since b1 is normally distribute, (b1 − β1)/σfb1g is a standard normal variable N(0; 1) I We don't know Var(b1) so it must be estimated from data. 2 We have already denoted it's estimate s fb1g I Using this estimate we it can be shown that b − β 1 1 ∼ t(n − 2) sfb1g where q 2 sfb1g = s fb1g It is from this fact that our confidence intervals and tests will derive. Where does this come from? I We need to rely upon (but will not derive) the following theorem For the normal error regression model SSE P(Y − Y^ )2 = i i ∼ χ2(n − 2) σ2 σ2 and is independent of b0 and b1. I Here there are two linear constraints P ¯ ¯ ¯ (Xi − X )(Yi − Y ) X Xi − X b1 = = ki Yi ; ki = P(X − X¯ )2 P (X − X¯ )2 i i i i b0 = Y¯ − b1X¯ imposed by the regression parameter estimation that each reduce the number of degrees of freedom by one (total two).
    [Show full text]
  • Sieve Bootstrap-Based Prediction Intervals for Garch Processes
    SIEVE BOOTSTRAP-BASED PREDICTION INTERVALS FOR GARCH PROCESSES by Garrett Tresch A capstone project submitted in partial fulfillment of graduating from the Academic Honors Program at Ashland University April 2015 Faculty Mentor: Dr. Maduka Rupasinghe, Assistant Professor of Mathematics Additional Reader: Dr. Christopher Swanson, Professor of Mathematics ABSTRACT Time Series deals with observing a variable—interest rates, exchange rates, rainfall, etc.—at regular intervals of time. The main objectives of Time Series analysis are to understand the underlying processes and effects of external variables in order to predict future values. Time Series methodologies have wide applications in the fields of business where mathematics is necessary. The Generalized Autoregressive Conditional Heteroscedasic (GARCH) models are extensively used in finance and econometrics to model empirical time series in which the current variation, known as volatility, of an observation is depending upon the past observations and past variations. Various drawbacks of the existing methods for obtaining prediction intervals include: the assumption that the orders associated with the GARCH process are known; and the heavy computational time involved in fitting numerous GARCH processes. This paper proposes a novel and computationally efficient method for the creation of future prediction intervals using the Sieve Bootstrap, a promising resampling procedure for Autoregressive Moving Average (ARMA) processes. This bootstrapping technique remains efficient when computing future prediction intervals for the returns as well as the volatilities of GARCH processes and avoids extensive computation and parameter estimation. Both the included Monte Carlo simulation study and the exchange rate application demonstrate that the proposed method works very well under normal distributed errors.
    [Show full text]
  • On Small Area Prediction Interval Problems
    ASA Section on Survey Research Methods On Small Area Prediction Interval Problems Snigdhansu Chatterjee, Parthasarathi Lahiri, Huilin Li University of Minnesota, University of Maryland, University of Maryland Abstract In the small area context, prediction intervals are often pro- √ duced using the standard EBLUP ± zα/2 mspe rule, where Empirical best linear unbiased prediction (EBLUP) method mspe is an estimate of the true MSP E of the EBLUP and uses a linear mixed model in combining information from dif- zα/2 is the upper 100(1 − α/2) point of the standard normal ferent sources of information. This method is particularly use- distribution. These prediction intervals are asymptotically cor- ful in small area problems. The variability of an EBLUP is rect, in the sense that the coverage probability converges to measured by the mean squared prediction error (MSPE), and 1 − α for large sample size n. However, they are not efficient interval estimates are generally constructed using estimates of in the sense they have either under-coverage or over-coverage the MSPE. Such methods have shortcomings like undercover- problem for small n, depending on the particular choice of age, excessive length and lack of interpretability. We propose the MSPE estimator. In statistical terms, the coverage error a resampling driven approach, and obtain coverage accuracy of such interval is of the order O(n−1), which is not accu- of O(d3n−3/2), where d is the number of parameters and n rate enough for most applications of small area studies, many the number of observations. Simulation results demonstrate of which involve small n.
    [Show full text]
  • Bayesian Prediction Intervals for Assessing P-Value Variability in Prospective Replication Studies Olga Vsevolozhskaya1,Gabrielruiz2 and Dmitri Zaykin3
    Vsevolozhskaya et al. Translational Psychiatry (2017) 7:1271 DOI 10.1038/s41398-017-0024-3 Translational Psychiatry ARTICLE Open Access Bayesian prediction intervals for assessing P-value variability in prospective replication studies Olga Vsevolozhskaya1,GabrielRuiz2 and Dmitri Zaykin3 Abstract Increased availability of data and accessibility of computational tools in recent years have created an unprecedented upsurge of scientific studies driven by statistical analysis. Limitations inherent to statistics impose constraints on the reliability of conclusions drawn from data, so misuse of statistical methods is a growing concern. Hypothesis and significance testing, and the accompanying P-values are being scrutinized as representing the most widely applied and abused practices. One line of critique is that P-values are inherently unfit to fulfill their ostensible role as measures of credibility for scientific hypotheses. It has also been suggested that while P-values may have their role as summary measures of effect, researchers underappreciate the degree of randomness in the P-value. High variability of P-values would suggest that having obtained a small P-value in one study, one is, ne vertheless, still likely to obtain a much larger P-value in a similarly powered replication study. Thus, “replicability of P- value” is in itself questionable. To characterize P-value variability, one can use prediction intervals whose endpoints reflect the likely spread of P-values that could have been obtained by a replication study. Unfortunately, the intervals currently in use, the frequentist P-intervals, are based on unrealistic implicit assumptions. Namely, P-intervals are constructed with the assumptions that imply substantial chances of encountering large values of effect size in an 1234567890 1234567890 observational study, which leads to bias.
    [Show full text]
  • 4.7 Confidence and Prediction Intervals
    4.7 Confidence and Prediction Intervals Instead of conducting tests we could find confidence intervals for a regression coefficient, or a set of regression coefficient, or for the mean of the response given values for the regressors, and sometimes we are interested in the range of possible values for the response given values for the regressors, leading to prediction intervals. 4.7.1 Confidence Intervals for regression coefficients We already proved that in the multiple linear regression model β^ is multivariate normal with mean β~ and covariance matrix σ2(X0X)−1, then is is also true that Lemma 1. p ^ For 0 ≤ i ≤ k βi is normally distributed with mean βi and variance σ Cii, if Cii is the i−th diagonal entry of (X0X)−1. Then confidence interval can be easily found as Lemma 2. For 0 ≤ i ≤ k a (1 − α) × 100% confidence interval for βi is given by È ^ n−p βi ± tα/2 σ^ Cii Continue Example. ?? 4 To find a 95% confidence interval for the regression coefficient first find t0:025 = 2:776, then p 2:38 ± 2:776(1:388) 0:018 $ 2:38 ± 0:517 The 95% confidence interval for β2 is [1.863, 2.897]. We are 95% confident that on average the blood pressure increases between 1.86 and 2.90 for every extra kilogram in weight after correcting for age. Joint confidence intervals for a set of regression coefficients. Instead of calculating individual confidence intervals for a number of regression coefficients one can find a joint confidence region for two or more regression coefficients at once.
    [Show full text]
  • 1 Confidence Intervals
    Math 143 – Inference for Means 1 Statistical inference is inferring information about the distribution of a population from information about a sample. We’re generally talking about one of two things: 1. ESTIMATING PARAMETERS (CONFIDENCE INTERVALS) 2. ANSWERING A YES/NO QUESTION ABOUT A PARAMETER (HYPOTHESIS TESTING) 1 Confidence intervals A confidence interval is the interval within which a population parameter is believed to lie with a mea- surable level of confidence. We want to be able to fill in the blanks in a statement like the following: We estimate the parameter to be between and and this interval will contain the true value of the parameter approximately % of the times we use this method. What does confidence mean? A CONFIDENCE LEVEL OF C INDICATES THAT IF REPEATED SAMPLES (OF THE SAME SIZE) WERE TAKEN AND USED TO PRODUCE LEVEL C CONFIDENCE INTERVALS, THE POPULATION PARAMETER WOULD LIE INSIDE THESE CONFIDENCE INTERVALS C PERCENT OF THE TIME IN THE LONG RUN. Where do confidence intervals come from? Let’s think about a generic example. Suppose that we take an SRS of size n from a population with mean µ and standard deviation σ. We know that the sampling µ √σ distribution for sample means (x¯) is (approximately) N( , n ) . By the 68-95-99.7 rule, about 95% of samples will produce a value for x¯ that is within about 2 standard deviations of the true population mean µ. That is, about 95% of samples will produce a value for x¯ that √σ µ is within 2 n of . (Actually, it is more accurate to replace 2 by 1.96 , as we can see from a Normal Distribution Table.) ( ) √σ µ µ ( ) √σ But if x¯ is within 1.96 n of , then is within 1.96 n of x¯.
    [Show full text]
  • Correlations & Confidence Intervals
    M140 Introducing Statistics • This tutorial will begin at 7:30pm for about 70 minutes. Correlations & • I will be recording this presentation so please let me know if you have any questions or concerns about this. • Mics will be muted until the end of the tutorial, Confidence when I will also stop recording. • Feel free to use the Chat Box at any time! • I will email slides out after the tutorial and post Intervals them on my OU blog. • Things you might need today: Dr Jason Verrall • M140 Book 4 [email protected] • Calculator 07311 188 800 • Note-taking equipment • Drink of your choice Tutorials are enhanced by your interaction Please vote in the polls and ask questions! M140 Introducing Statistics Correlations & Confidence Intervals • Scatter Plots & Correlations • r values • Correlation & Causation • Confidence Intervals Computer Book has • Prediction Intervals detailed instructions! • Plus Minitab examples But you don’t need Minitab running today 2 Scatter Plots Scatter Plots & Correlations 1) Which is the positive relationship? A Variable 2 Variable Variable 1 B Variable 2 Variable Variable 1 3 Scatter Plots Scatter Plots & Correlations 1) Which is the positive relationship? A Variable 2 Variable Variable 1 B Variable 2 Variable Variable 1 4 Scatter Plots Scatter Plots & Correlations Scatterplots are notoriously tricky to interpret unless very clear, particularly the strength of any relationship 5 Scatter Plots Scatter Plots & Correlations Scatterplots are notoriously tricky to interpret unless very clear, particularly the strength
    [Show full text]
  • Lecture 32 the Prediction Interval Formulas for the Next Observation from a Normal Distribution When Σ Is Unknown
    Lecture 32 The prediction interval formulas for the next observation from a normal distribution when σ is unknown 1 Introduction In this lecture we will derive the formulas for the symmetric two-sided prediction interval for the n + 1-st observation and the upper-tailed prediction interval for the n+1-st observation from a normal distribution when the variance σ2 is unknown.We will need the following theorem from probability theory that gives the distribution of the statistic X − Xn +1. Suppose that X1,X2,...,Xn,Xn+1 is a random sample from a normal distribution with mean µ and variance σ2. − q n+1 Theorem 1. The random variable T =(X Xn+1)/( n S) has t distribution with n − 1 degrees of freedom. 2 The two-sided prediction interval formula Now we can prove the theorem from statistics giving the required prediction interval for the next observation xn+1 in terms of n observations x1,x2, ··· ,xn. Note that it is symmetric around X. This is one of the basic theorems that you have to learn how to prove. There are also asymmetric two-sided prediction intervals. − q n+1 q n+1 Theorem 2. The random interval (X tα/2,n−1 n S,X + tα/2,n−1 n S) is a 100(1 − α)%-prediction interval for xn+1. 1 Proof. We are required to prove rn +1 rn +1 P (X ∈ (X − t S,X + t S)) = 1 − α. n+1 α/2,n−1 n α/2,n−1 n We have rn +1 rn +1 LHS = P (X − t S<X ,X < X + t S)=P (X − X <t α/2,n−1 n n+1 n+1 α/2,n−1 n n+1 α/2,n− rn +1 rn +1 = P (X − X <t S,X − X > −t S) n+1 α/2,n−1 n n+1 α/2,n−1 n rn +1 rn +1 = P ((X − X )/ S<t , (X − X )/ S>−t ) n+1 n α/2,n−1 n+1 n α/2,n−1 =P (T<tα/2,n−1 ,T>−tα/2,n−1)=P (−tα/2,n−1 <T<tα/2,n−1)=1− α To prove the last equality draw a picture.
    [Show full text]
  • Chapters 2 and 10: Least Squares Regression
    Chapters 2 and 10: Least Squares Regression Learning goals for this chapter: Describe the form, direction, and strength of a scatterplot. Use SPSS output to find the following: least-squares regression line, correlation, r2, and estimate for σ. Interpret a scatterplot, residual plot, and Normal probability plot. Calculate the predicted response and residual for a particular x-value. Understand that least-squares regression is only appropriate if there is a linear relationship between x and y. Determine explanatory and response variables from a story. Use SPSS to calculate a prediction interval for a future observation. Perform a hypothesis test for the regression slope and for zero population correlation/independence, including: stating the null and alternative hypotheses, obtaining the test statistic and P-value from SPSS, and stating the conclusions in terms of the story. Understand that correlation and causation are not the same thing. Estimate correlation for a scatterplot display of data. Distinguish between prediction and extrapolation. Check for differences between outliers and influential outliers by rerunning the regression. Know that scatterplots and regression lines are based on sample data, but hypothesis tests and confidence intervals give you information about the population parameter. When you have 2 quantitative variables and you want to look at the relationship between them, use a scatterplot. If the scatter plot looks linear, then you can do least squares regression to get an equation of a line that uses x to explain what happens with y. The general procedure: 1. Make a scatter plot of the data from the x and y variables. Describe the form, direction, and strength.
    [Show full text]
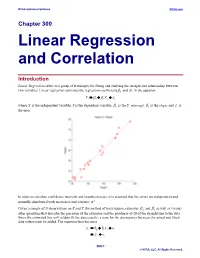
  • Linear Regression and Correlation
    NCSS Statistical Software NCSS.com Chapter 300 Linear Regression and Correlation Introduction Linear Regression refers to a group of techniques for fitting and studying the straight-line relationship between two variables. Linear regression estimates the regression coefficients β0 and β1 in the equation Yj = β0 + β1 X j + ε j where X is the independent variable, Y is the dependent variable, β0 is the Y intercept, β1 is the slope, and ε is the error. In order to calculate confidence intervals and hypothesis tests, it is assumed that the errors are independent and normally distributed with mean zero and variance σ 2 . Given a sample of N observations on X and Y, the method of least squares estimates β0 and β1 as well as various other quantities that describe the precision of the estimates and the goodness-of-fit of the straight line to the data. Since the estimated line will seldom fit the data exactly, a term for the discrepancy between the actual and fitted data values must be added. The equation then becomes y j = b0 + b1x j + e j = y j + e j 300-1 © NCSS, LLC. All Rights Reserved. NCSS Statistical Software NCSS.com Linear Regression and Correlation where j is the observation (row) number, b0 estimates β0 , b1 estimates β1 , and e j is the discrepancy between the actual data value y j and the fitted value given by the regression equation, which is often referred to as y j . This discrepancy is usually referred to as the residual. Note that the linear regression equation is a mathematical model describing the relationship between X and Y.
    [Show full text]