DOCSLIB.ORG

POPULATION GENETICS LECTURE NOTES-2016.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
POPULATION GENETICS LECTURE NOTES-2016.Pdf Training course in Quantitative Genetics and Genomics Biosciences East and Central Africa- International Livestock Research Institute (BecA-ILRI) Hub Nairobi, KENYA May 30-June 10, 2016 POPULATION AND QUANTITATIVE GENETICS GENOME ORGANIZATION AND GENETIC MARKERS SELECTION THEORY BREEDING STRATEGIES Samuel E Aggrey, PhD Professor Department of Poultry Science Institute of Bioinformatics University of Georgia Athens, GA 30602, USA [email protected] Preface This lecture notes was written in an attempt to cover parts of Population Genetics, Quantitative Genetics and Molecular Genetics for postgraduate students and also as a refresher for field geneticists. The course material is not a text book and not meant to be copied, duplicated or sold. This text is unedited and I am solely responsible for all conceptual mistakes, grammatical errors and typos. Genetics is a life-long course and cannot be covered in a few lectures. Only selected parts of the population- and quantitative-, and molecular genetics will be covered in this course because of time constraints. This course will cover some of the evolutionary changes in allele frequency between generations such as natural selection and gene flow, and some aspects of Quantitative and Molecular Genetics. To those men who have kept us awake for over two centuries and I believe would continue to do so for many more centuries! POPULATION GENETICS The study of composition of biological populations, and changes in genetic composition that result from operation of various factors including (a) natural selection, (b) genetic drift, (c) mutations and (d) gene flow Genetic composition Population 1. The number of alleles at a locus A group of breeding 2. The frequency of alleles at a locus individuals 3. The frequency of genotypes at a locus 4. Transmission of alleles from one generation to the next Single locus: Locus A with two alleles A1 and A2 p =P +½H q =Q +½H Derivation of the Hardy-Weinberg principle Ideal population 1. Two sexes and the population consist of sexually mature individuals 2. Mating between male and female are equal in probability (independent of distance between mates, type of genotype, age of individuals 3. Population is large and actual frequency of each mating is equal to Mendelian expectation 1 4. Meiosis is fair. We assume that there is no segregation distortion, no gamete competition, no differences in the developmental ability of eggs or fertilizing ability of sperms 5. All mating produce the same number of offspring, on average. Thus, frequency of a particular genotype in the pool of newly formed zygote is: ∑(frequency of mating) (frequency of genotype produced from mating) Frequency (A1A1 in zygotes) = P2 + ½PH +½PH +¼H2 =(P+½H)2 =p2 Frequency (A1A2) =2pq Frequency (A2A2) =q2 6. Generations do not overlap 7. There is no difference among genotype groups in the probability of survival 8. There is no migration, mutation, drift and selection Hardy-Weinberg Law In a large random mating population in the absence of mutation, migration, selection and random drift, allele frequency remains the same from generation to generation. Furthermore, there is a simple relationship between allele frequency and genotypic frequency Why is Hardy-Weinberg principle so important? Is there any population anywhere in the world or outer space that satisfies all assumptions? Possible evolutionary forces within populations cause a violation of at least one of these assumptions, and departure from Hardy-Weinberg are one way in which we detect those forces and estimate their magnitude. The most significant evolutionary factors are selection (natural or artificial), non-random mating and gene flow. 2 Fig. 1 shows the relationship between allele frequency and three genotypic frequencies for a population under Hardy-Weinberg proportions: 1. The heterozygote is the most common genotype for intermediate allele frequencies 2. One of the homozygotes is the most when the allele frequency is not intermediate 3. Only ⅓ of the time when q is between ⅓ and ⅔, is the heterozygote the most common genotype 4. When q is between 0 and ⅓ A1A1 is the most common, and when q is between ⅔ and 1, A2A2 is the most common. 5. The maximum frequency of the heterozygote occurs when q=0.5 This can be shown directly by setting the derivatives of the H-W heterozygosity, 2pq=2q(1-q), equal to zero and solving for q or d[2q(1 − q) = 2 − 4푞 = 0 푑푞 Here, we assume that the generations are non-overlapping, i.e. the parents die after producing progeny, and the progeny then become the next parental generation. Testing for deviation from Hardy-Weinberg Equilibrium Departure from Hardy-Weinberg equilibrium can be tested from a sample scored for their genotypes. The genetic model provided by Hardy-Weinberg generates the expected frequency at equilibrium. We can now compare observed and expected allele frequencies under the assumptions of Hardy-Weinberg proportions. The chi- square test of goodness of fit and the likelihood ratio test can be used to test departure or lack thereof from Hardy-Weinberg equilibrium. The chi-square test is an approximation to the likelihood ratio test. To perform a chi-square goodness of fit test, we first have to estimate the observed genotypic frequency from the data, 3 then use that to generate the expected genotypic frequencies. We can compute the chi-square statistic as: (푂 − 퐸)2 푋2 = ∑ 퐸 Where O and E are the observed and expected number of a particular genotype and n is the number of genotypic classes. From the calculated value of X2 and the table value of X2 we can obtain the probability that the observed numbers deviates from the expected numbers. The degrees of freedom used to determine the significance of X2 value are equal to the number of genotypic classes, n, minus one, then minus the number of parameters estimated from the data. One degree of freedom is always lost because we use the data to estimate allele frequency. We can use the chi-square distribution to test whether the value of X2 is too large to be the result of sampling error. In doing so we are performing a one-tailed test. The chi-square expression for two alleles is given as: (푁 − p̂2N)2 (푁 − 2p̂q̂N)2 (푁 − q̂2N)2 푋2 = 11 + 12 + 22 p̂N 2p̂q̂ N q̂2N An alternate way to estimate differences of observed frequencies from expected frequencies is to calculate the standardized deviation of the observed frequency from the Hardy-Weinberg expectation of heterozygotes, which provides the fixation index or generally inbreeding, F. 2푝푞 − 퐻 퐻 퐹 = = 1 − 2푝푞 2푝푞 It can be shown that 푋2 = 퐹2푁 For two alleles, the Chi-square good of fit test for Hardy-Weinberg proportions is equivalent to the test for inbreeding, F=0. However, F is unstable as the expected (E) value approaches zero, and therefore not useful for rare and very common alleles. For E=0, O>0, F=-∞, and for E=0, and O=0, F is undefined. Deviation from Hardy-Weinberg proportions can also be tested using the likelihood ratio test which is described in most statistical texts. 4 The B/b locus is responsible for plumage color in chickens found in the Rift Valley. The B allele expresses black plumage which is completely dominant over the b allele for brown plumage. Phenotype Genotype Observed number Expected number Black BB 290 p̂ 2N=289.444 Black Bb 496 2p̂ q̂ =497.112 Brown bb 214 q̂ 2N=213.444 Total 1,000 1,000 P=290/1000=0.29; H=496/1000=0.496; Q=214/1000=0.214; P+H+Q=1.0 p̂ =P+½H = 0.29+½(0.496)=0.538; q̂ =Q+½H = 0.214+½(0.496)=0.462; p̂ +q̂ =1.0 Note: Chi-square is allergic to fraction and ratios, but really likes integers! (290 − 289.444)2 (496 − 497.112)2 (214 − 213.444)2 푋2 = + + = 0.0050 289.444 497.112 213.444 The X2-Table at p=0.05 at 1 degree of freedom is 3.84. Since the X2 calculate is lower than X2 table, we can conclude that the data does not deviate from Hardy- Weinberg proportions. 퐻 0.496000 퐹 = 1 − = 1 − = 0.002237 2푝푞 0.497112 푋2 = 퐹2푁 = 0.0050 5 Extension of Hardy-Weinberg’s Law: Multiple Alleles Let us consider a single locus with three alleles A1, A2 and A3 with frequencies, p, q and r, respectively. Hardy Weinberg frequencies for three autosomal alleles at a single locus Allele/ A1 A2 A3 frequency p q r A1 A1A1 A1A2 A1A3 p p2 pq pr A2 A2A1 A2A2 A2A3 q qp q2 qr A3 A3A1 A3A3 A3A3 r rp rq r2 Genotype Frequency Number 2 A1A1 p N11 A1A2 pq+pq=2pq N12 A1A3 pr+pr=2pr N13 2 A2A2 q N22 A2A3 qr+qr=2qr N23 2 A3A3 r N33 TOTAL 1.0 N Please note that, 푝 + 푞 + 푟 = 1, and they key to solving multiple alleles is to break in order for the problem to resemble a two allele problem 푁 푓(퐴3퐴3) = 푟2 = 33 푁 푁 푟 = √ 33 푁 From here, let’s reduce the problem to a two allele locus involving the allele, A3 Expected genotypes under H-W: A2A2, A2A3 and A3A3 with expected frequency 푁 +푁 +푁 푞2 + 2푞푟 + 푟2 = 22 23 33. 푁 From basic algebra: (푎 + 푏)2 = 푎2 + 2푎푏 + 푏2. This implies: (푞 + 푟)2 = 푞2 + 2푞푟 + 푟2 푁 +푁 +푁 Therefore: (푞 + 푟)2 = 22 23 33 푁 6 푁 +푁 +푁 푞 + 푟 = √ 22 23 33 푁 푁 +푁 +푁 푁 푟 = √ 22 23 33 − √ 33 푁 푁 Since, 푝 + 푞 + 푟 = 1, then 푝 = 1 − (푞 + 푟) 푁 +푁 +푁 푝 = 1 − √ 22 23 33 푁 The ABO blood group in humans is determined by three alleles, A, B and O.
Load more

Recommended publications
  • And Ford, I; Ford, '953) on the Other Hand Have Put Forward a View Intermediate Between the Extreme Ones of Darwin on the One Hand and Goldschmidt on the Other
    THE EVOLUTION OF MIMICRY IN THE BUTTERFLY PAPILIO DARDANUS C. A. CLARKE and P. M. SHEPPARD Departments of Medicine and Zoology, University of Liverpool Received23.V.59 1.INTRODUCTION WHENBatesputforward the mimicry hypothesis which bears his name, Darwin (1872), although accepting it, had some difficulty in explaining the evolution of the mimetic resemblance of several distinct species to one distasteful model by a series of small changes, a require- ment of his general theory of evolution. He said "it is necessary to suppose in some cases that ancient members belonging to several distinct groups, before they had diverged to their present extent, accidentally resembled a member of another and protected group in a sufficient degree to afford some slight protection; this having given the basis for the subsequent acquisition of the most perfect resemb- lance ". Punnett (1915) realised that the difficulty is even more acute when one is dealing with a polymorphic species whose forms mimic very distantly related models. Knowing that, in those butterflies which had been investigated genetically, the forms differed by single allelomorphs he concluded that the mimicry did not evolve gradually and did not confer any advantage or disadvantage to the individual. He argued that an allelomorph arises at a single step by mutation and that therefore the mimicry also arises by chance at a single step. Goldschmidt (x) although not denying that mimicry confers some advantage to its possessors also maintained that the resemblance arises fully perfected by a single mutation of a gene distinct from that producing the colour pattern in the model, but producing a similar effect in the mimic.
    [Show full text]
  • Special Issues on Advances in Quantitative Genetics: Introduction
    Heredity (2014) 112, 1–3 & 2014 Macmillan Publishers Limited All rights reserved 0018-067X/14 www.nature.com/hdy EDITORIAL Special issues on advances in quantitative genetics: introduction Heredity (2014) 112, 1–3; doi:10.1038/hdy.2013.115 Fisher’s (1918) classic paper on the inheritance of complex traits not While much of the focus was on standard biometrical applications only founded the field of quantitative genetics, but also coined the (for example, variance components), hints of things to come were term variance and introduced the powerful statistical method of foreshadowed by papers on the relevance of molecular biology to analysis of variance. This was a watershed paper, reconciling the breeding and applications of mixed models (models including both Mendelian’s discrete and saltatorial view of trait evolution with the fixed and random effects, for example, BLUP and REML). Much of gradual and continuous view of Darwin’s followers, the biometricians the emphasis was on breeding or laboratory populations. A decade (Provine, 1971). This fusion of Mendelian genetics with Darwinian later, the second ICQG held at Raleigh, North Carolina in 1987 natural selection was the start of the modern evolutionary synthesis. (Weir et al., 1988), reflected explosive growth in new tools (low- Fisher’s paper also marked a critical point in modern statistics, and density molecular markers for early quantitative trait locus (QTL) this synergism between the development of new statistical methods mapping), a continued expansion of the importance of mixed-model and the ever-increasing complexity of genetic/genomic data sets methodology for complex estimation issues, and a growing fusion of continues to this day.
    [Show full text]
  • Microevolution and the Genetics of Populations ​ ​ Microevolution Refers to Varieties Within a Given Type
    Chapter 8: Evolution Lesson 8.3: Microevolution and the Genetics of Populations ​ ​ Microevolution refers to varieties within a given type. Change happens within a group, but the descendant is clearly of the same type as the ancestor. This might better be called variation, or adaptation, but the changes are "horizontal" in effect, not "vertical." Such changes might be accomplished by "natural selection," in which a trait ​ ​ ​ ​ within the present variety is selected as the best for a given set of conditions, or accomplished by "artificial selection," such as when dog breeders produce a new breed of dog. Lesson Objectives ● Distinguish what is microevolution and how it affects changes in populations. ● Define gene pool, and explain how to calculate allele frequencies. ● State the Hardy-Weinberg theorem ● Identify the five forces of evolution. Vocabulary ● adaptive radiation ● gene pool ● migration ● allele frequency ● genetic drift ● mutation ● artificial selection ● Hardy-Weinberg theorem ● natural selection ● directional selection ● macroevolution ● population genetics ● disruptive selection ● microevolution ● stabilizing selection ● gene flow Introduction Darwin knew that heritable variations are needed for evolution to occur. However, he knew nothing about Mendel’s laws of genetics. Mendel’s laws were rediscovered in the early 1900s. Only then could scientists fully understand the process of evolution. Microevolution is how individual traits within a population change over time. In order for a population to change, some things must be assumed to be true. In other words, there must be some sort of process happening that causes microevolution. The five ways alleles within a population change over time are natural selection, migration (gene flow), mating, mutations, or genetic drift.
    [Show full text]
  • New Strategies and Tools in Quantitative Genetics: How to Go from the Phenotype to the Genotype
    PP68CH16-Loudet ARI 6 April 2017 9:43 ANNUAL REVIEWS Further Click here to view this article's online features: • Download figures as PPT slides • Navigate linked references • Download citations New Strategies and Tools in • Explore related articles • Search keywords Quantitative Genetics: How to Go from the Phenotype to the Genotype Christos Bazakos, Mathieu Hanemian, Charlotte Trontin, JoseM.Jim´ enez-G´ omez,´ and Olivier Loudet Institut Jean-Pierre Bourgin, INRA, AgroParisTech, CNRS, Universite´ Paris-Saclay, 78026 Versailles Cedex, France; email: [email protected] Annu. Rev. Plant Biol. 2017. 68:435–55 Keywords First published online as a Review in Advance on genetic architecture, QTL, RIL, GWAS, phenotype February 6, 2017 The Annual Review of Plant Biology is online at Abstract plant.annualreviews.org Quantitative genetics has a long history in plants: It has been used to study https://doi.org/10.1146/annurev-arplant-042916- specific biological processes, identify the factors important for trait evolu- 040820 Annu. Rev. Plant Biol. 2017.68:435-455. Downloaded from www.annualreviews.org tion, and breed new crop varieties. These classical approaches to quantitative Copyright c 2017 by Annual Reviews. trait locus mapping have naturally improved with technology. In this review, All rights reserved we show how quantitative genetics has evolved recently in plants and how new developments in phenotyping, population generation, sequencing, gene Access provided by INRA Institut National de la Recherche Agronomique on 05/05/17. For personal use only. manipulation, and statistics are rejuvenating both the classical linkage map- ping approaches (for example, through nested association mapping) as well as the more recently developed genome-wide association studies.
    [Show full text]
  • Patterns and Power of Phenotypic Selection in Nature
    Articles Patterns and Power of Phenotypic Selection in Nature JOEL G. KINGSOLVER AND DAVID W. PFENNIG Phenotypic selection occurs when individuals with certain characteristics produce more surviving offspring than individuals with other characteristics. Although selection is regarded as the chief engine of evolutionary change, scientists have only recently begun to measure its action in the wild. These studies raise numerous questions: How strong is selection, and do different types of traits experience different patterns of selection? Is selection on traits that affect mating success as strong as selection on traits that affect survival? Does selection tend to favor larger body size, and, if so, what are its consequences? We explore these questions and discuss the pitfalls and future prospects of measuring selection in natural populations. Keywords: adaptive landscape, Cope’s rule, natural selection, rapid evolution, sexual selection henotypic selection occurs when individuals with selection on traits that affect survival stronger than on those Pdifferent characteristics (i.e., different phenotypes) that affect only mating success? In this article, we explore these differ in their survival, fecundity, or mating success. The idea and other questions about the patterns and power of phe- of phenotypic selection traces back to Darwin and Wallace notypic selection in nature. (1858), and selection is widely accepted as the primary cause of adaptive evolution within natural populations.Yet Darwin What is selection, and how does it work? never attempted to measure selection in nature, and in the Selection is the nonrandom differential survival or repro- century following the publication of On the Origin of Species duction of phenotypically different individuals.
    [Show full text]
  • Quantitative Genetics of Gene Expression and Methylation in the Chicken
    Andrey Höglund Linköping Studies In Science and Technology Dissertation No. 2097 FACULTY OF SCIENCE AND ENGINEERING Linköping Studies in Science and Technology, Dissertation No. 2097, 2020 Quantitative genetics Department of Physics, Chemistry and Biology Linköping University SE-581 83 Linköping, Sweden of gene expression Quantitative genetics of gene expression and methylation the in chicken www.liu.se and methylation in the chicken Andrey Höglund 2020 Linköping studies in science and technology, Dissertation No. 2097 Quantitative genetics of gene expression and methylation in the chicken Andrey Höglund IFM Biology Department of Physics, Chemistry and Biology Linköping University, SE-581 83, Linköping, Sweden Linköping 2020 Cover picture: Hanne Løvlie Cover illustration: Jan Sulocki During the course of the research underlying this thesis, Andrey Höglund was enrolled in Forum Scientium, a multidisciplinary doctoral program at Linköping University, Sweden. Linköping studies in science and technology, Dissertation No. 2097 Quantitative genetics of gene expression and methylation in the chicken Andrey Höglund ISSN: 0345-7524 ISBN: 978-91-7929-789-3 Printed in Sweden by LiU-tryck, Linköping, 2020 Abstract In quantitative genetics the relationship between genetic and phenotypic variation is investigated. The identification of these variants can bring improvements to selective breeding, allow for transgenic techniques to be applied in agricultural settings and assess the risk of polygenic diseases. To locate these variants, a linkage-based quantitative trait locus (QTL) approach can be applied. In this thesis, a chicken intercross population between wild and domestic birds have been used for QTL mapping of phenotypes such as comb, body and brain size, bone density and anxiety behaviour.
    [Show full text]
  • An Introduction to Quantitative Genetics I Heather a Lawson Advanced Genetics Spring2018 Outline
    An Introduction to Quantitative Genetics I Heather A Lawson Advanced Genetics Spring2018 Outline • What is Quantitative Genetics? • Genotypic Values and Genetic Effects • Heritability • Linkage Disequilibrium and Genome-Wide Association Quantitative Genetics • The theory of the statistical relationship between genotypic variation and phenotypic variation. 1. What is the cause of phenotypic variation in natural populations? 2. What is the genetic architecture and molecular basis of phenotypic variation in natural populations? • Genotype • The genetic constitution of an organism or cell; also refers to the specific set of alleles inherited at a locus • Phenotype • Any measureable characteristic of an individual, such as height, arm length, test score, hair color, disease status, migration of proteins or DNA in a gel, etc. Nature Versus Nurture • Is a phenotype the result of genes or the environment? • False dichotomy • If NATURE: my genes made me do it! • If NURTURE: my mother made me do it! • The features of an organisms are due to an interaction of the individual’s genotype and environment Genetic Architecture: “sum” of the genetic effects upon a phenotype, including additive,dominance and parent-of-origin effects of several genes, pleiotropy and epistasis Different genetic architectures Different effects on the phenotype Types of Traits • Monogenic traits (rare) • Discrete binary characters • Modified by genetic and environmental background • Polygenic traits (common) • Discrete (e.g. bristle number on flies) or continuous (human height)
    [Show full text]
  • Quantitative Genetics and Heritability of Growth-Related Traits in Hybrid Striped Bass (Morone Chrysops ♀×Morone Saxatilis ♂)
    Aquaculture 261 (2006) 535–545 www.elsevier.com/locate/aqua-online Quantitative genetics and heritability of growth-related traits in hybrid striped bass (Morone chrysops ♀×Morone saxatilis ♂) Xiaoxue Wang a, Kirstin E. Ross b, Eric Saillant a, ⁎ Delbert M. Gatlin III a, John R. Gold a, a Center for Biosystematics and Biodiversity, Department of Wildlife and Fisheries Sciences, Texas A&M University, College Station, TX 77843-2258, USA b Department of Environmental Health, Flinders University, Adelaide, SA, 5001, Australia Received 30 November 2005; received in revised form 19 July 2006; accepted 21 July 2006 Abstract Commercially farmed, hybrid striped bass – female white bass (Morone chrysops) crossed with male striped bass (Morone saxatilis) – represent a rapidly growing industry in the United States. Expanded production of hybrid striped bass, however, is limited because of uncontrolled variation in performance of fish derived from undomesticated broodstock. A 10×10 factorial mating design was employed to examine genetic effects and heritability of growth-related traits based on dam half-sib and sire half- sib families. A total of 881 offspring were raised in a common environment and body weight and length were recorded at three different times post-fertilization; parentage of each fish was inferred from genotypes at 10 nuclear-encoded microsatellites. Dam and sire effects on juvenile growth (weight and length) and growth rate were significant, whereas dam by sire interaction effect was not. The dam and sire components of variance for weight and length (at age) and growth rate were estimated using a Restricted Maximum Likelihood algorithm. Estimates of broad-sense heritability of weight, using a family-mean basis, ranged from 0.67± 0.17 to 0.85±0.07 for dams; estimates for sires ranged from 0.43±0.20 to 0.77±0.10.
    [Show full text]
  • Contribution and Perspectives of Quantitative Genetics to Plant Breeding in Brazil
    Contribution and perspectives of quantitative genetics to plant breeding in Brazil Crop Breeding and Applied Biotechnology S2: 7-14, 2012 Brazilian Society of Plant Breeding. Printed in Brazil Contribution and perspectives of quantitative genetics to plant breeding in Brazil Roland Vencovsky1, Magno Antonio Patto Ramalho2* and Fernando Henrique Ribeiro Barrozo Toledo1 Received 15 September 2012 Accepted 03 October 2012 Abstract – The purpose of this article is to show how quantitative genetics has contributed to the huge genetic progress obtained in plant breeding in Brazil in the last forty years. The information obtained through quantitative genetics has given Brazilian breeders the possibility of responding to innumerable questions in their work in a much more informative way, such as the use or not of hybrid cultivars, which segregating population to use, which breeding method to employ, alternatives for improving the efficiency of selec- tion programs, and how to handle the data of progeny and/or cultivars evaluations to identify the most stable ones and thus improve recommendations. Key words: Genetic parameters, genotype by environment interaction, hybrid cultivars, stability and adaptability. INTRODUCTION Therefore, this article was written up with the purpose of commenting some of the innumerable aspects of quantitative Plant breeding has been conceptualized in different genetics in Brazil that contributed to decision-making of manners throughout its history. In the concept proposed by breeders, creating good managers and, above all, showing Kempthorne (1957) “plant breeding is applied quantitative that in recent decades, many decisions of Brazilian breeders genetics.” Considering that he was a biometrician, it is easy have been based on knowledge from quantitative genetics.
    [Show full text]
  • Arise by Chance As the Result of Mutation. They Therefore Suggest
    THE EVOLUTION OF DOMINANCE UNDER DISRUPTIVE SELECTION C. A. CLARKE and P. Ni. SHEPPARD Department of Medicine and Department of Zoology, University of Liverpool Received6.iii.59 1.INTRODUCTION INa paper on the effects of disruptive selection, Mather (1955) pointed out that if there are two optimum values for a character and all others are less advantageous or disadvantageous there will be disruptive selection which can lead to the evolution of a polymorphism. Sheppard (1958) argued that where such selection is effective and the change from one optimum value to the other is switched by a single pair of allelomorphs there will be three genotypes but only two advantageous phenotypes. Consequently if dominance were absent initially it would be evolved as a result of the disruptive selection, the heterozygote and one of the homozygotes both coming to resemble one of the two optimum phenotypes (see Ford, 1955, on Tripharna comes). Thoday (1959) has shown by means of an artificial selection experiment that, even when a character is, at the beginning, controlled polygenically (sternopleural chaeta-number in Drosophila) and there is 50 per cent. gene exchange between the "high" and "low" selected sub-popu- lations, a polymorphism can evolve. The most fully understood examples of disruptive selection (other than sex) are provided by instances of Batesian Mimicry, where there are a number of distinct warningly coloured species, acting as models, which are mimicked by the polymorphic forms of a single more edible species. Fisher and Ford (see Ford, 1953) have argued that a suffi- ciently good resemblance between mimic and model is not likely to arise by chance as the result of mutation.
    [Show full text]
  • Quantitative and Population Genetics
    Genome 371, 8 March 2010, Lecture 15 Quantitative and Population Genetics • What are quantitative traits and why do we care? - genetic basis of quantitative traits - heritability • Basic concepts of population genetics Final is Monday, March 15 8:30 a.m. Hogness Auditorium - in Health Sciences room A420 What Phenotypes/Diseases Do You Find Most Interesting? Quantitative Genetics • Concerned with the inheritance of differences between individuals that are a matter of degree rather than kind (i.e., quantitative not qualitative) Mice Fruit Flies In:Introduction to Quantitative Genetics Falconer & Mackay 1996 Many Discrete Traits Have an Underlying Quantitative Basis Serum Glucose Levels Some Puzzling Aspects of Quantitative Traits • Legendary debate in the early 1900’s on the genetic basis of quantitative traits -vs- “Mendelian” “Biometrician” • Genes are discrete and should lead to discrete phenotypes R- r r Sir Ronald Fisher To the Rescue 1918 paper “The Correlation Between Relatives on the Supposition of Mendelian Inheritance” reconciled this conflict Showed that inherently discontinuous variation caused by genetic segregation is translated into the continuous variation of quantitative characters Genetic Basis of Quantitative Traits First, we need a model: single locus with alleles A and a Familiar model Additive model one allele is dominant (uppercase) Active allele (uppercase) other allele is recessive (lowercase) Inactive allele (lower case) aa AA, Aa aa Aa AA 6 gms 14 gms 6 gms 10 gms 14 gms A General Additive Single Locus Model If
    [Show full text]
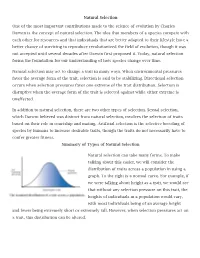
  • Natural Selection One of the Most Important Contributions Made to The
    Natural Selection One of the most important contributions made to the science of evolution by Charles Darwin is the concept of natural selection. The idea that members of a species compete with each other for resources and that individuals that are better adapted to their lifestyle have a better chance of surviving to reproduce revolutionized the field of evolution, though it was not accepted until several decades after Darwin first proposed it. Today, natural selection forms the foundation for our understanding of how species change over time. Natural selection may act to change a trait in many ways. When environmental pressures favor the average form of the trait, selection is said to be stabilizing. Directional selection occurs when selection pressures favor one extreme of the trait distribution. Selection is disruptive when the average form of the trait is selected against while either extreme is unaffected. In addition to natural selection, there are two other types of selection. Sexual selection, which Darwin believed was distinct from natural selection, involves the selection of traits based on their role in courtship and mating. Artificial selection is the selective breeding of species by humans to increase desirable traits, though the traits do not necessarily have to confer greater fitness. Summary of Types of Natural Selection Natural selection can take many forms. To make talking about this easier, we will consider the distribution of traits across a population in using a graph. To the right is a normal curve. For example, if we were talking about height as a trait, we would see that without any selection pressure on this trait, the heights of individuals in a population would vary, with most individuals being of an average height and fewer being extremely short or extremely tall.
    [Show full text]