Linear Estimation in Krein Spaces
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Current Affairs Quiz – August, September & October for IBPS Exams
Current Affairs Quiz – August, September & October for IBPS Exams August - Current Affairs Quiz: Q.1) The Rajya Sabha passed the Constitution Q.8) Who came up with a spirited effort to beat _____ Bill, 2017 with amendments for setting up Florian Kaczur of Hungary and finish second in of a National Commission for Backward Classes, the Czech International Open Chess tournament was passed after dropping Clause 3. at Pardubidze in Czech Republic? a) 121st b) 122nd c) 123rd a) Humpy Koneru b) Abhijeet Gupta d) 124th e) 125th c) Vishwanathan Anand d) Harika Dronavalli Q.2) From which month of next year onwards e) Tania Sachdev government has ordered state-run oil companies Q.9) Which country will host 2024 summer to raise subsidised cooking gas, LPG, prices by Olympics? four rupees per cylinder every month to eliminate a) Japan b) Australia c) India all the subsidies? d) France e) USA a) January b) February c) March Q.10) Who beats Ryan Harrison to claim fourth d) April e) May ATP Atlanta Open title, he has reached the final in Q.3) Who will inaugurate the two-day Conclave of seven of eight editions of the tournament, added Tax Officers ―Rajaswa Gyansangam‖ scheduled to a fourth title to those he won in 2013, 2014 and be held on 1st and 2nd September, 2017 in New 2015? Delhi? a) Roger Federer b) Nick Kyrgios a) Arun Jaitley b) Narendra Modi c) Andy Murray d) John Isner c) Rajnath Singh d) Nitin Gadkari e) Kevin Anderson e) Narendra Singh Tomar Q.11) Who was the youngest of the famous seven Q.4) The Executive Committee of National Mission ‗Dagar Bandhus‘ and had dedicated his life to for Clean Ganga (4th meeting) approved seven keeping the Dhrupad tradition alive, died projects worth Rs _____ crore in the sector of recently. -
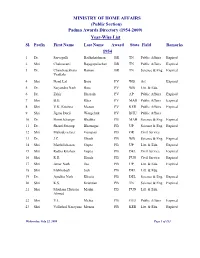
(Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl
MINISTRY OF HOME AFFAIRS (Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl. Prefix First Name Last Name Award State Field Remarks 1954 1 Dr. Sarvapalli Radhakrishnan BR TN Public Affairs Expired 2 Shri Chakravarti Rajagopalachari BR TN Public Affairs Expired 3 Dr. Chandrasekhara Raman BR TN Science & Eng. Expired Venkata 4 Shri Nand Lal Bose PV WB Art Expired 5 Dr. Satyendra Nath Bose PV WB Litt. & Edu. 6 Dr. Zakir Hussain PV AP Public Affairs Expired 7 Shri B.G. Kher PV MAH Public Affairs Expired 8 Shri V.K. Krishna Menon PV KER Public Affairs Expired 9 Shri Jigme Dorji Wangchuk PV BHU Public Affairs 10 Dr. Homi Jehangir Bhabha PB MAH Science & Eng. Expired 11 Dr. Shanti Swarup Bhatnagar PB UP Science & Eng. Expired 12 Shri Mahadeva Iyer Ganapati PB OR Civil Service 13 Dr. J.C. Ghosh PB WB Science & Eng. Expired 14 Shri Maithilisharan Gupta PB UP Litt. & Edu. Expired 15 Shri Radha Krishan Gupta PB DEL Civil Service Expired 16 Shri R.R. Handa PB PUN Civil Service Expired 17 Shri Amar Nath Jha PB UP Litt. & Edu. Expired 18 Shri Malihabadi Josh PB DEL Litt. & Edu. 19 Dr. Ajudhia Nath Khosla PB DEL Science & Eng. Expired 20 Shri K.S. Krishnan PB TN Science & Eng. Expired 21 Shri Moulana Hussain Madni PB PUN Litt. & Edu. Ahmed 22 Shri V.L. Mehta PB GUJ Public Affairs Expired 23 Shri Vallathol Narayana Menon PB KER Litt. & Edu. Expired Wednesday, July 22, 2009 Page 1 of 133 Sl. Prefix First Name Last Name Award State Field Remarks 24 Dr. -

Convex Programming-Based Phase Retrieval: Theory and Applications
Convex programming-based phase retrieval: Theory and applications Thesis by Kishore Jaganathan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2016 Defended May 16, 2016 ii © 2016 Kishore Jaganathan All Rights Reserved iii To my family and friends. iv En vazhi thani vazhi (my way is a unique way). - Rajnikanth v ACKNOWLEDGEMENTS Firstly, I would like to express my sincere gratitude to my advisor Prof. Babak Hassibi. I could not have imagined having a better advisor and mentor for my Ph.D. studies. His immense knowledge, guidance, kindness and support over the years have played a crucial role in making this work possible. My understanding of many topics, including convex optimization, signal processing and entropy vectors, have significantly increased because of him. His exceptional problem solving abilities, teaching qualities and deep understanding of a wide variety of subjects have inspired me a lot. Furthermore, the intellectual freedom he offered throughout the course of my graduate studies helped me pursue my passion and grow as a research scientist. Besides my advisor, I am also extremely indebted to Prof. Yonina C. Eldar. I have been privileged to have had the opportunity to collaborate with her. Her vision and ideas have played a very important role in shaping this work. Her vast knowledge, attention to detail, work ethic and energy have influenced me significantly. Additionally, I would like to thank her for providing me the opportunity to contribute to a book chapter on phase retrieval. I would also like to thank Prof. -

Partial Differential Equations
CALENDAR OF AMS MEETINGS THIS CALENDAR lists all meetings which have been approved by the Council pnor to the date this issue of the Nouces was sent to press. The summer and annual meetings are joint meetings of the Mathematical Association of America and the Ameri· can Mathematical Society. The meeting dates which fall rather far in the future are subject to change; this is particularly true of meetings to which no numbers have yet been assigned. Programs of the meetings will appear in the issues indicated below. First and second announcements of the meetings will have appeared in earlier issues. ABSTRACTS OF PAPERS presented at a meeting of the Society are published in the journal Abstracts of papers presented to the American Mathematical Society in the issue corresponding to that of the Notices which contains the program of the meet ing. Abstracts should be submitted on special forms which are available in many departments of mathematics and from the office of the Society in Providence. Abstracts of papers to be presented at the meeting must be received at the headquarters of the Society in Providence, Rhode Island, on or before the deadline given below for the meeting. Note that the deadline for ab stracts submitted for consideration for presentation at special sessions is usually three weeks earlier than that specified below. For additional information consult the meeting announcement and the list of organizers of special sessions. MEETING ABSTRACT NUMBER DATE PLACE DEADLINE ISSUE 778 June 20-21, 1980 Ellensburg, Washington APRIL 21 June 1980 779 August 18-22, 1980 Ann Arbor, Michigan JUNE 3 August 1980 (84th Summer Meeting) October 17-18, 1980 Storrs, Connecticut October 31-November 1, 1980 Kenosha, Wisconsin January 7-11, 1981 San Francisco, California (87th Annual Meeting) January 13-17, 1982 Cincinnati, Ohio (88th Annual Meeting) Notices DEADLINES ISSUE NEWS ADVERTISING June 1980 April 18 April 29 August 1980 June 3 June 18 Deadlines for announcements intended for the Special Meetings section are the same as for News. -

IFL Annual Return 2018-19
FORM NO. MGT-7 Annual Return [Pursuant to sub-Section(1) of section 92 of the Companies Act, 2013 and sub-rule (1) of rule 11of the Companies (Management and Administration) Rules, 2014] Form language English Hindi Refer the instruction kit for filing the form. I. REGISTRATION AND OTHER DETAILS (i) * Corporate Identification Number (CIN) of the company Pre-fill Global Location Number (GLN) of the company * Permanent Account Number (PAN) of the company (ii) (a) Name of the company (b) Registered office address (c) *e-mail ID of the company (d) *Telephone number with STD code (e) Website (iii) Date of Incorporation (iv) Type of the Company Category of the Company Sub-category of the Company (v) Whether company is having share capital Yes No (vi) *Whether shares listed on recognized Stock Exchange(s) Yes No (b) CIN of the Registrar and Transfer Agent Pre-fill Name of the Registrar and Transfer Agent Page 1 of 15 Registered office address of the Registrar and Transfer Agents (vii) *Financial year From date 01/04/2018 (DD/MM/YYYY) To date 31/03/2019 (DD/MM/YYYY) (viii) *Whether Annual general meeting (AGM) held Yes No (a) If yes, date of AGM 24/09/2019 (b) Due date of AGM 30/09/2019 (c) Whether any extension for AGM granted Yes No II. PRINCIPAL BUSINESS ACTIVITIES OF THE COMPANY *Number of business activities 1 S.No Main Description of Main Activity group Business Description of Business Activity % of turnover Activity Activity of the group code Code company I I2 III. PARTICULARS OF HOLDING, SUBSIDIARY AND ASSOCIATE COMPANIES (INCLUDING JOINT VENTURES) *No. -

(CHAPTER V , PARA 25) FORM 9 List of Applications for Inclusion
ANNEXURE 5.8 (CHAPTER V , PARA 25) FORM 9 List of Applications for inclusion received in Form 6 Designated location identity (where Constituency (Assembly/£Parliamentary): IRINJALAKKUDA Revision identity applications have been received) 1. List number@ 2. Period of applications (covered in this list) From date To date 16/11/2020 16/11/2020 3. Place of hearing * Serial number$ Date of receipt Name of claimant Name of Place of residence Date of Time of of application Father/Mother/ hearing* hearing* Husband and (Relationship)# 1 16/11/2020 Pradeep Erattu Kamala Velayudhan (M) 271, Kattoor, Thrissur, , velayudhan 2 16/11/2020 Elwin Roy . Shajitha Roy roy (M) Chittilappilly , Kattur, Irinjalakuda, , 3 16/11/2020 AARIA MARY A G DAVID (F) ALAPPATT HOUSE , KATTOOR, KATTOOR, , 4 16/11/2020 SMITHA T R BASHEER T M (H) THATHARAPARAMBIL , KATTUNGACHIRA, IRINJALAKUDA, , 5 16/11/2020 ROBIN PAILY PAILY E V (F) ELENJIKKAL HOUSE, MAPRANAM, MADAYIKONAM, , 6 16/11/2020 SIBIN SHAJAN SHAJAN P J (F) PERUMBULLY, MAPRANAM, MADAYIKONAM, , 7 16/11/2020 GODWIN MALIYEKKAL TONY (F) 0, Manthripuram south, Irinjalakuda, , 8 16/11/2020 ASHWITA RAJESH RAJESH P G (F) PACHERI HOUSE, NADAVARAMBA, VELOOKKARA, , 9 16/11/2020 Vinay Balraj Bindu (M) Thathamath, Avittathur , Velookkara, , £ In case of Union territories having no Legislative Assembly and the State of Jammu and Kashmir Date of exhibition at @ For this revision for this designated location designated location under Date of exhibition at Electoral * Place, time and date of hearings as fixed by electoral registration officer rule 15(b) Registration Officer¶s Office under $ Running serial number is to be maintained for each revision for each designated rule 16(b) location # Give relationship as F-Father, M=Mother, and H=Husband within brackets i.e. -

Patrika-March 2013.Pmd
No. 57 March 2013 Newsletter of the Indian Academy of Sciences Seventy-Eighth Annual Meeting, Dehra Dun 2 – 4 November 2012 The 78th Annual Meeting of the Academy, hosted by the Wadia Institute of Himalayan Geology in Dehra Dun over November 2–4, 2012, saw a return to this venue after nineteen years, the previous Annual Meeting in Inside.... this city having been in 1993. Thanks to its location in the Himalayan foothills, and the proximity to many 1. Seventy-Eighth Annual Meeting, Dehra Dun places of historic interest, the attendance was very 2 – 4 November 2012 .......................................... 1 good – 135 Fellows, 11 Associates and 47 invited 2. Twenty-Fourth Mid-Year Meeting teachers. 5 – 6 July 2013 ..................................................... 4 The packed three day 3. 2013 Elections ........................................................ 6 programme included, apart from the opening 4. Special Issues of Journals ..................................... 7 Presidential address, two 5. Discussion Meetings ............................................... 9 Special Lectures, two 6. ‘Women in Science’ Panel Programmes .............. 13 evening Public Lectures, two mini Symposia, and 7. STI Policy – Brainstorming Session .................... 15 presentations by 19 Fellows 8. Raman Professor .................................................. 15 and Associates. The Presidential address by Professor A. K. Sood, the 9. Summer Research Fellowship Programme ......... 16 concluding one for the triennium 2010-2012, carried forward -

Curriculum Vitae of Thomas Kailath
Curriculum Vitae-Thomas Kailath Hitachi America Professor of Engineering, Emeritus Information Systems Laboratory, Dept. of Electrical Engineering Stanford, CA 94305-9510 USA Tel: +1-650-494-9401 Email: [email protected], [email protected] Fields of Interest: Information Theory, Communication, Computation, Control, Linear Systems, Statistical Signal Processing, VLSI systems, Semiconductor Manufacturing and Lithography. Probability Theory, Mathematical Statistics, Linear Algebra, Matrix and Operator Theory. Home page: www.stanford.edu/~tkailath Born in Poona (now Pune), India, June 7, 1935. In the US since 1957; naturalized: June 8, 1976 B.E. (Telecom.), College of Engineering, Pune, India, June 1956 S.M. (Elec. Eng.), Massachusetts Institute of Technology, June, 1959 Thesis: Sampling Models for Time-Variant Filters Sc.D. (Elec. Eng.), Massachusetts Institute of Technology, June 1961 Thesis: Communication via Randomly Varying Channels Positions Sep 1957- Jun 1961 : Research Assistant, Research Laboratory for Electronics, MIT Oct 1961-Dec 1962 : Communications Research Group, Jet Propulsion Labs, Pasadena, CA. He also held a part-time teaching appointment at Caltech Jan 1963- Aug 1964 : Acting Associate Professor of Elec. Eng., Stanford University (on leave at UC Berkeley, Jan-Aug, 1963) Sep 1964-Jan 1968 : Associate Professor of Elec. Eng. Jan 1968- Feb 1968 : Full Professor of Elec. Eng. Feb 1988-June 2001 : First holder of the Hitachi America Professorship in Engineering July 2001- : Hitachi America Professorship in Engineering, Emeritus; recalled to active duty to continue his research and writing activities. He has also held shorter-term appointments at several institutions around the world: UC Berkeley (1963), Indian Statistical Institute (1966), Bell Labs (1969), Indian Institute of Science (1969-70, 1976, 1993, 1994, 2000, 2002), Cambridge University (1977), K. -

Mgl-Int-1-2015-Unpaid Shareholders List As on 31
MGL-INT-1-2015-UNPAID SHAREHODLERS LIST AS ON 31-10-2017 DEMAT ID_FOLIO NAME WARRANT NO MICR DIVIDEND AMOUNT ADDRESS 1 ADDRESS 2 ADDRESS 3 ADDRESS 4 CITY PINCODE JH1 JH2 001431 JITENDRA DATTA MISRA 1500046 522 10800.00 BHRATI AJAY TENAMENTS 5 VASTRAL RAOD WADODHAV PO AHMEDABAD 382415 001424 BALARAMAN S N 1500056 532 18000.00 14 ESOOF LUBBAI ST TRIPLICANE MADRAS 600005 001209 PANCHIKKAL NARAYANAN 1500061 537 18000.00 NANU BHAVAN KACHERIPARA KANNUR KERALA 670009 001440 RAJI GOPALAN 1500072 548 18000.00 ANASWARA KUTTIPURAM THIROOR ROAD KUTTYPURAM KERALA 679571 1204470005875147 VANAJA MUKUNDAN 1500137 613 10602.00 1/297A PANAKKAL VALAPAD GRAMA PANCHAYAT THRISSUR 680567 1204760000162413 HAMSA K S 1500163 639 15570.00 KOOTTUNGAPARAMBIL HOUSE NEAR NASEEB AUDITORIUM THALIKULAM THRISSUR 680569 004215 PRINCE A.P. 1500174 650 21600.00 ARIMBOOR CHEEROTHA HOUSE KANJANY POST THRISSUR 680612 000050 HAJI M.M.ABDUL MAJEED 1500176 652 18000.00 MUKRIAKATH HOUSE VATANAPALLY TRICHUR DIST. KERALA 680614 1204760000219351 SHAJIN N V 1500206 682 18000.00 NADUMURI HOUSE PUTHENCHIRA KOMBATHUKADAVU P O THRISSUR 680682 REKHA SHAJIN 001237 MENON C B 1500217 693 18000.00 PANAMPILLY HOUSE ANNAMANABI THRISSUR KERALA 680741 001468 THOMAS JOHN 1500234 710 18000.00 THOPPIL PEEDIKAYIL KARTHILAPPALLY ALLEPPEY KERALA 690516 THOMAS VARGHESE 000483 NASSAR M.K. 1500240 716 1800.00 MOONAKAPARAMBIL HOUSE CHENTHRAPINNI TRICHUR DIST. KERALA MRS. ABIDA NASSAR 000524 HAMZA A.P. 1500241 717 1800.00 ARAYAMPPARABIL HOUSE ANDATHODE KERALA MRS. HAMZA A.P. 000642 JNANAPRAKASH P.S. 1500246 722 1800.00 POZHEKKADAVIL HOUSE P.O.KARAYAVATTAM TRICHUR DIST. KERALA STATE 68056 MRS. LATHA M.V. 000671 SHEFABI K M 1500247 723 1800.00 C/O.SEENATH HUSSAIN CHINNAKKAL HOME PO. -

A View of Three Decades of Linear Filtering Theory
146 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. IT-20, NO. 2, MARCH 1974 A View of Three Decades of Linear Filtering Theory Invited Paper THOMAS KAILATH, FELLOW, IEEE Abstrucf-Developments in the theory of linear least-squares estima- fields; problems of scalar and matrix polynomial factoriza- tion in the last thirty years or so are outlined. Particular attention is tion with applications in network theory and stability paid to early mathematical. wurk in the field and to more modem develop- theory [135], [177] ; the solution of linear equations, ments showing some of the many connections between least-squares filtering and other fields. especially as they arise in constructing state-variable realizations from impulse-response or transfer-function I. IN~~DUCTION AND OUTLINE data, which in turn is related to the Berlekamp-Massey HE SERIES of survey papers of which this is a part algorithm for decoding BCH codes [289], [191]; and the was begun largely to commemorate the twenty-fifth inversion of multivariable linear systems [357], [361], anniversaryT of the publication of Shannon’s classic paper [362]. There are also more purely mathematical ramifica- on information theory. However, 1974 is also twenty-five tions in Hilbert-space theory, operator theory, and more years after the publication in the open literature of Wiener’s generally in functional analysis [245], [250], [261]. famous monograph, “Extrapolation, Interpolation and The section headings give a quick idea of the scope of Smoothing of Stationary Time Series, with Engineering the paper. Applications” [I], so that it is appropriate this year to I. Introduction. commemorate this event as well. -

| the Loyolite 2007 | Our School Song
1 | The Loyolite 2007 | Our School Song Cheer Loyola’s sons Virtue shielding us Cheer till day is done Knowledge for our weapon Till the game is won Onward ,on , Loyola’s sons. For our School. Let us march asinging As her banners soar Send the echoes ringing Let the echoes roar Giving our best till the game is won. Round the golden shore Of India’s rule. Oh, thou God of all Hear us when we call Virtue shielding us Help us one and all Knowledge for our weapon By Thy grace, Onward ,on , Loyola’s sons. When life’s game is done Let us march asinging And the victory won Send the echoes ringing May we wear the crown Giving our best till the game is won. Of joy and grace. Loyola’s sons, acclaim Virtue shielding us Brave Loyola’s fame Knowledge for our weapon Proud to bear the name Onward ,on , Loyola’s sons. O’er the field Let us march asinging Always brave and true Send the echoes ringing Pledge each day anew Giving our best till the game is won. Aye to dare and do Ne’er to yield. The Loyolite 2007 Loyola School Thiruvananthapuram EDITORIAL BOARD Editor Ms Deepa Pillai English Ms Brinda Nair Mr Prathap Chandran Ms Mary Mathew Ms Nandini Unnikrishnan Ms Maitri Rath Hindi Ms Anita Ms Sathi A Malayalam Mr Ramesan Ms Renu R C Student Editors Joshua George Nikhil P Joseph Gurudas S Avinesh V Sriram P Kevin Sabu Peter Mishel Johns Tushar Nair Consultant Bhattathiri Printed at Published by Rev Fr Varghese Anikuzhy S J | The Loyolite 2007 Principal, Loyola School, Trivandrum 4 The Editorial Board is happy to welcome you to The Loyolite 2007. -
Mgl- Int 3- 2014
DIVIDENT WARRANT FOLIO_DEAMT ID NAME MICR ADDRESS 1 ADDRESS 2 ADDRESS 3 ADDRESS 4 CITY PINCOD JH1 JH2 AMOUNT NO 900013 DR.ABHISHEK K.M. 378000.00 70024 S/O.DR.K.K.MOHANDAS KOZHIPARAMBIL HOUSE KOORKANCHERY P.O THRISSUR 001221 DWARKA NATH ACHARYA 180000.00 70033 5 JAG BANDHU BORAL LANE CALCUTTA 700007 001431 JITENDRA DATTA MISRA 10800.00 70048 524 BHRATI AJAY TENAMENTS 5 VASTRAL RAOD WADODHAV PO AHMEDABAD 382415 001424 BALARAMAN S N 18000.00 70059 535 14 ESOOF LUBBAI ST TRIPLICANE MADRAS 600005 001209 PANCHIKKAL NARAYANAN 18000.00 70065 541 NANU BHAVAN KACHERIPARA KANNUR KERALA 670009 001440 RAJI GOPALAN 18000.00 70074 550 ANASWARA KUTTIPURAM THIROOR ROAD KUTTYPURAM KERALA 679571 IN30089610488366 RAKESH P UNNIKRISHNAN 10193.00 70085 561 KRISHNA AYYANTHOLE P O THRISSUR THRISSUR 680003 IN30163741039292 NEENAMMA VINCENT 10958.00 70097 573 PLOT NO103 NEHRUNAGAR KURIACHIRA THRISSUR 680006 IN30169610530267 SUDHINAWALES 19800.00 70106 582 NO 2/585 SUDHIN APARTMENTS PATTURAKKAL TRICHUR KERALA 680022 1204760000051455 SUNIL A R 14400.00 70145 621 ARAYAMPARAMBIL HOUSE KARAYAMUTTAM POST VALAPAD 680567 RAJAN A S 1204760000184619 SABIYA FAISEL 18000.00 70172 648 THACHILLATH HOUSE CHERKKARA TALIKULAM POST THRISSUR 680569 001960 GEORGE A I 18000.00 70185 661 ATHIYUMDHAN HOUSE PO KANDASSANKADAVU TRICHUR KERALA 680613 JOY A G BABU A G 000050 HAJI M.M.ABDUL MAJEED 18000.00 70187 663 MUKRIAKATH HOUSE VATANAPALLY TRICHUR DIST. KERALA 680614 002495 SAJEEV M R 13500.00 70232 708 C/O.RAGHAVA PISHARODY 7/142 "KRISHNA" PUTHENVELIKARA ERNAKULAM DIST 683594 001468 THOMAS JOHN 18000.00 70244 720 THOPPIL PEEDIKAYIL KARTHILAPPALLY ALLEPPEY KERALA 690516 THOMAS VARGHESE 000483 NASSAR M.K.