DOCSLIB.ORG

In Partial Fulfilment of the Requirements for the Degree of It{Aster of Science

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
In Partial Fulfilment of the Requirements for the Degree of It{Aster of Science The University of Manitoba Optimal Operation of a Flood Control Systen by John Nairn MacKenzie A Thesis Submitted to the Faculty of Graduate Studies in Partial Fulfilment of the Requirements for the Degree of It{aster of Science Tl¡-nr+man+ l'ir¡i'l DePdL Llllu.lIL ^.Ê\JI \,-LVI-L FnoinoarinoLtlSrIrçvf rrrð WitIrIulft/võ, nn i nco l\4en i toba Arrmrcf I q7R C)PTiIIAL OPEIIAÏIÛN OT A FLOOD CÛNTRC]L SYSÏËi4 BY JOHN I.IÄIRÎ''J I.4¡CKEI{Z] E A clissertation submiÈted to tåte Facr*lty of Cr*ci".¡aÉe Stuse.åies of' tlre University oá' Munitoba ire partLrl f'uifilln'le¡rt ol' t!re requle'ernemts ol'tlre clegrce ot IIAST TR OF S C I ENC E o,ig78 Fernrissio¡r hus bec¡r gnunted Ëo the t-l¡ì$l,AÊLV ûF Te!U U¡{l\¡¡-:F¿- S¡TV Ol.' h{.4þ]lTO!3"4 tr¡ lenei q¡r s¿:l! copies oü t!¡is cåÈ*;ertati{!r¡" 8o the N,4TltNAL [.N8¡4,ARY ûFr {lA"l\Ai}A to l¡riar¡:*'ilrsr tl¡ls ciissertafio¡r and tr: lend or sell copies of the felnr, und {,JNl'VUåì,5åTY h{lCfì,OFlLh{S tr: pubiish i¡¡r ahsåraet of this rJissert¿¡f ion. The ar¡thor re$erve$ otå:cr publ!c¿¡Èir¡¡r rights, ¿¡¡rJ ¡"¡either the dissertation ncr exÉensive cxtri¡cfs fr¡:nr it mluy h*: gx'int*d eir otl¡er- wise repi:oeíLlced evithout t !¡c uuf l¡o¡''s writËc¡r 3:cnrr ieslr.xr" ACI$IOWLEDffiIvE\TS I would like to e4press my appTeciation to my advisor, Professor G. Booy for his guidance and patience throughout the somewhat long gestation period of this thesis. I would also like to express my appreciation to Mr. P. Flatt of charles Howard and Associates, consulting Engineers, for making avail- able the linear progranrning solution algorithm used in this thesis and his comments regarding the solution algorithm in particular and the linear programning technique in general- I would like to express my most sincere appreciation to my wife, l-1'aLrrv LvrrtJnnmletion - l\4nninrro fnr her Ëll\-U(Jfên..ìrlr^2ocmcnf dBclllurr L @lILfenrl nafPa LlLlrLv ience thrc"^]^^"rLlrr uutslrvuL of the thesis. II onbruol^l TABLE OF CONTENTS Page Acl,noivledgements i I i cf nf Fi or rrpq Vi 1.0 INTRODUCTION 2 1.1 A Flood Control System La 7.2 Sinulation Analysis 3 | ( f lnlrmf 7aT1î\'**-rr furdaj/5_L> 4 7.4 Optimization-Símulation Comparison 5 r.J1 q T'harlrv r-ÌnfimirationvIJur¡ttr¿ l4ode1 Selected in this Tþesis 6 2.0 TTIE ASSINIBOINE RIVER SYSTEM l-U 2.I History 10 2.2 Flood Control Tnvestigations 10 2.3 Shellmouth Reservoir 72 2.4 Assiniboine River Diversion 13 3.O THE GENERAL LINEAR PROGRA}O4ING Ì\4ODEL FOR A FLOOD CONTROL SYSTEM 22 3. 1 The Linear Progranming Tecirnique 22 3.2 The }{odel Descríption 25 3.3 Linear Progrannning }lodel Coirstraints 3.3.7 Physical Constraints 27 3 .3.7.7 Storage Constraints 27 3.3.7.2 Reservoir Mass Balance Constraint 28 111 Table of Contents cont. Ðc'_*Þ: ¡a 3.3.I.3 Reservoir Release Constraint 28 3.3.7.4 Cha:r¡rel Continuity of Storage Constraint 29 3 .3 .1.5 RiParian Constraint 29 3.3.7.6 Diversion Capacity Constraint JU 3.3.1.7 Upper Limit on Diversion Flow Values 30 3.3.2 Coniputational- Constraints 3L 3.3.2.I Peak Discharge Constraint 3L 3.3.2.2 Non-Negativity Constraint 32 3.4 Objective Functíon )L 3.5 Time Dependency of Objective Fr-urctíon at Danage Centres 33 3.6 NonlinearitY 35 3.7 Size of the Linear Progranu.ning Problem 3B 3.7.7 Elinination of Variable Qi^t 38 3.7.2 Elinination of Fixed Valued Variables 39 4.0 ftIE LINEAR PROGRA}MING MODEL APPLIED TO 'IT]E ASSINIBOINE RIVER SYSTM,Í 46 4.7 TLe Assiniboine River lt{odel 46 4.2 Study Operational Rules 47 4.3 Flood Damage Fulctions 4B 4.4 Specific Linear Prograruning }lode1 for the Assjniboine River SYstem 53 4.4.I Physical Constraints 53 4.4.7.I Storage Constraints 53 4.4.7.2 Reservoir Mass Balance Equation 53 4.4.7.3 Reservoir Release Constraint trA Table of Contents cont. T)a¡a 4.4.7.4 Riparian Constraint 54 4.4.L.5 Diversion Capacity Constraint 55 4.4.7.6 Upper Limit on Divcrsion Florv Values 55 4 .4.2 Contputational Constraints 56 4.4.2.1 Peak Discharge Constraint 56 4.5 Sumrmry of Problem Constraints 57 5. 0 COIPUTATIONAL TECFil{IQUES 77 5.1 Ïte ComPuter lt{odel 77 5.2 lt{atrix Generator 77 5.3 Thc Liucar Plogramning Solution Algorithm 79 5 .4 'Ihe RePort Writer 79 6.0 RESULTS B2 6.1 The Optirriization }4ode1 BZ 6.2 Discr-rssion of Results 84 6.3 Model Run Cost B6 6 .4 Surnurary Conclus ions B7 APPENDIX A 100 APPENDIX B L46 BIBLIORAPFry 1s8 LIS'I OF FIüMES Þa oa II-1 Assiniboine River Drainage Basín 77 II-2 Shellnouth Reservoir, Location 1B II-'3 Assiniboine River Díversion, Location 19 II=4 Assiniboine River Diversion, Layout Details 20 III.1 Sanple Linear Progranirning Problent 47 III=2 Hypothetical River Basin System 42 III-5 Definítion of Tine periods used in Aria11'sis A7 III-4 Scparable Programning Example Figure 44 IV-1 Assiniboine River Drainage Basin IV-2 l\ratcr Sur-vey of Canada Streamflow Gauging Locations in the Study Area 64 IV-3 Discharge Damage Relationship - Assiniboine Rir¡er at Russell 65 IV-4 Discharge Damagc Relationship - Assiniboine River al- Ir{iniota 66 n^*^ n^1^+: TV- 5 Di sclrarse UcLllldgv^^ L l-uj^*^llio l>.--r - Assiniboine River AL Þ- ^f'-Ld Brandon 67 a1- IV-6 Discharge Damage Relationship - Assiniboine River dL Pnrt:oe le Prairie 68 IV-7 Discharge Damage Relationship - Assiniboine River Diversion ov rr--^-^ Tr^1^+;'^-^hin TV-B Discharp-e----- ò- lJdllidgE r\Uf d Ll-\-rlI>rrrlr - /Ass'inìboine LJJ !rrruvri River !{oodino1 er¡ 70 V1 List of Figures coqt_. T)c ra IV-9 Discharge Damage fte1atíonsìlip - Assiniboine Ríver at l\Tinnipeg /I ry-10 Elevation.Ðisc]-iarge Relationsliip Shellmouth Reservoir 72 W-11 Elevation=storage Rclationship Shcllmouth Reservoir 73 IV-72 Outflow-storage Relationship Shellmouth Resen'oir 74 IV=13 Schematic Repr-esentation of Assiniboiire River Basin 75 W-1 Natural and Optimal Flow Values, Russell BB VÍ-2 Natural and Optimal Flow Val.ues, tr{iniota 89 VI-3 Natural and Optimal Flor.^¡ Values, Blandon 90 VI-4 Natural and Optimal Flow Values, Portage 1a Prairie 91 VI-S Natural arrd Optimal Florv Values, I"leadingley ^a 'l{imipeg Vi - 6 Natural and Optinal Flow Values , VI-7 Optimal Shellmouth Reservoir Operating Schedule 94 VI-8 Optinal Assiniboine River Divelsion Operating Schedule 95 \iI-9 Output fr'om Report lfriter 96 VI-10 Output from RePort l\rriter 97 VI-11 Output from Rcport j\'riter 98 vii 1.0 INIRODUCTION OPTIMAL OPERATION OF A FLOOD CONTROL SYSTEM 1.0 INTRODUCTION 1.1 A Flood Control SYstem Two kinds of flood control works may be actively operated in order to alleviate flood danage, reservoirs and diversiors. Reservoirs reduce flood damage by storing flood waters and releasing them at a later date so as to reduce the peak of the flood wave and lengthen its duration. Diversions sinply divert flood waters away to an area less prone to flood damage. An operable flood control system as discussed in this thesis is composed of reservoirs and diversions in addition to passive flood con- trol rvorks such as dykes. The object of operation of any flood control system is to minimlze flood damage. This requirement defines the optimal operating schedule for each of the system components. The degree of complexity of the op- timal operation of a flood control systeilì is deternined by the nr¡rber of flood control reseryoirs and/or diversions which conrprise the system for each flood control component requires its oirrn operating schedule. Since the operating schedules of the components of the system may be hi-ghly inter-related it may be appreciated that the difficulty in arriving at optinal operating schedules increases very rapidly as the ru.mber of com- ponents of the flood control systen increases. The opti-mal operating procedure is based on anticipated florvs. The r:ncertainty in forecasting flows therefore adds a degree of r.rncertaintY to the optimal operating procedure. It need not add to the complexity of the analysis if the rincertainty itself is not a factor in the objec- tive of the system oPeration. 2 In this thesis all flow values have been treated as being determin- istic and no allowance for stochastic variation has been included. Stochastic variation of flow values could be addressed by mearìs of new estinates of flow values which would then be subject to another analysis. In an operational flood control context this might take the form of a high, best and low estimate of systen in flows with each estimate re- quiring a separate analysis. In this manner any stochastic variation in flow estimates can be partially addressed within the deterministic frame- work of the model constructed in a nanner acceptable for operational flood control ÐurDoses, 7.2 Sinrulation Analysis Sinrulation analysis is a conmonly accepted method of arrivi¡rg at an operating schedule for a flood control systen. In a simulation analysis, the river system is modelled so that movement in time and space of river flows throughout the river basin may be simulated.
Load more

Recommended publications
  • Flood Fighting in Manitoba
    Flood Fighting in Manitoba A History and Background of Manitoba’s Flood Protection Works Flood Fighting in Manitoba Southern Manitoba has extensive flood control Flood protection work has prevented property measures in place, particularly in the Red River damage and reduced the potential impact of Valley, from Winnipeg, south to the US border. flooding on families and communities. Since Flood controls were built after the devastating flood the 1997 flood, more than $1 billion has been of 1950, which flooded the Red River Valley and invested in flood mitigation efforts in Manitoba. the City of Winnipeg. Construction of the Red River This investment has prevented over $7 billion in Floodway was completed in 1968. Additional flood damages throughout Manitoba. control improvements, including an expansion of the The 2011 flood affected a large geographic floodway, were made after the Flood of the area and thousands of Manitobans. Early flood Century in 1997. This flood was substantially larger forecasts and flood-mitigation efforts helped many than the 1950 flood, but resulted in far less property communities get a head start on protecting homes damage because of the flood control measures in and lands, but damage was still widespread. place. There are also flood control measures along the Assiniboine River. Flood Control Infrastructure in Southern Manitoba DauDpahuinp hRiniv Reriver ! ! LakLeake FirsFt iNrsat tNioantion WaWterahteernhen WinWninipneigpoesgiossis LakLea kSet. SMta. rMtianrtin RivReriver DikDesikes " W"aWtearhteernhen LakLea kSet. SMta. rMtianrtin DuDcuk ck DikDesikes LittLleit tSlea sSkaastkcahtecwhaenwan " " EmEemrgeerngceyn Ccyh aCnhnaenlnel MoMuonutanitna in DikDesikes " " ProPvr.o Pv.a Prkark FairFfoairrdford LaLkeake MoMssoeyssey FirsFt iNrsat tNioanti!on !St.S Mt.
    [Show full text]
  • Red River Floodway Operation Report Spring 2019
    RED RIVER FLOODWAY OPERATION REPORT SPRING 2019 June 28, 2019 Manitoba Infrastructure Hydrologic Forecasting and Water Management Branch Water Management and Structures Division Printed on Recycled Paper EXECUTIVE SUMMARY The 2019 Red River spring flood resulted from above normal to well above normal winter snow fall in the upper Red River basin, including significant late season snowfall in the Fargo area, combined with normal soil moisture going into freeze-up in the fall. The March Outlook published by Manitoba’s Hydrologic Forecast Center estimated that the peak flow at Emerson could exceed the flow seen in the 2011 flood under favorable conditions, and exceed the 2009 flood under normal conditions. Under unfavorable conditions, the 2019 flow at Emerson was forecast to be second only to 1997 in the last 60 years of records. The observed peak at Emerson for the 2019 spring flood was approximately 60,700 cfs (1720.0 m3/s), and occurred on April 25. This is similar to the peak flow observed at Emerson in 2010. The 2019 peak flow measured at Emerson equated to a 1:15 year flood. However, due to the small contributions of tributaries in the lower portion of the basin, the peak natural flood flow at James Avenue only equated to a 1:6 year flood. The 2019 Red River spring flood was driven primarily by significant winter precipitation in the upper portion of the basin, and most of the tributaries on the Canadian side of the border had peaked long before the flood crest arrived. Ice was not a major concern on the Red or Assiniboine rivers in 2019, however, some ice jamming did occur north of the City of Winnipeg in the Selkirk and Netley Creek areas.
    [Show full text]
  • Manitoba's Flood of 2011
    Manitoba’s Flood of 2011 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • Steve Topping, P. Eng Executive Director, Regulatory and Operational Services Manitoba Water Stewardship September 13 , 2011 why was there so much water this year? why this flood was so different than 1997? was this a record-breaking year? Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth •2010 was the 5th wettest September through February on record following the first wettest on record (2009) and 3rd wettest (2010). October 26-28th 2010 Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography Snow Pack 2011 •Snowfall totals 75 to 90 inches, nearly double the climatological average. Newdale: 6-7 ft snow depth Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring • Storm events at the wrong time •15th year of current wet cycle, resulting in very little storage in the soils Why was there so much water? • Antecedent Soil Moisture – April-October 2010 • Snow Moisture, Density and Depth • Geography • Precipitation this Spring • Storm events at the wrong time • Many watersheds flooding simultaneously May Sun Mon Tues Wed Thurs Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Pre-Flood Preparation • Supplies and Equipment • 3 amphibex icebreakers • 7 ice cutting machines • 3 amphibious ATVs • 3 million sandbags • 30,000 super sandbags • 3 sandbagging units (total of 6) • 24 heavy duty steamers (total of 61) • 43 km of cage barriers • 21 mobile pumps (total of 26) • 72 km of water filled barriers • and much more...
    [Show full text]
  • Executive Summary
    Page 1 of 26 Hydrologic Forecast Centre Manitoba Infrastructure Winnipeg, Manitoba FEBRUARY FLOOD OUTLOOK February 26, 2021 Executive Summary The February Flood Outlook prepared by the Hydrologic Forecast Centre of Manitoba Infrastructure reports the risk of major spring flooding in most Manitoba basins is low. Due to below normal soil moisture at freeze-up in southern and central Manitoba basins and below normal to well below normal winter precipitation until mid-February in these basins, the risk of major spring flooding is low for all southern and central Manitoba basins. Southern and central Manitoba basins include the Assiniboine River, Red River, Souris River, Pembina River, Roseau River and Qu’Appelle River basins and Interlake region. The risk of major spring flooding is low to moderate for northern Manitoba basins, including the Saskatchewan and Churchill River basins, because these basins have normal to above normal soil moisture and received below normal to slightly above normal winter precipitation. Most of the major lakes are below normal levels for this time of the year and within their operating ranges. The risk of flooding for most lakes is low. Soil Moisture Conditions at Freeze up: Soil moisture at freeze-up is one of the major factors that affects spring runoff potential and spring flood risk. Due to normal to below normal summer and fall precipitation, the soil moisture at freeze-up is normal to below normal for most of the southern and central Manitoba basins. Soil moisture is normal to above normal in the Little Saskatchewan River basin and in areas close to Brandon.
    [Show full text]
  • Provincial Flood Control Infrastructure Review of Operating Guidelines
    A REPORT TO THE MINISTER OF MANITOBA INFRASTRUCTURE AND TRANSPORTATION August 2015 2 - Provincial Flood Control Infrastructure Panel Members Harold Westdal Chair Rick Bowering Hydrological Engineer Barry MacBride Civil Engineer Review of Operating Guidelines - 3 ACKNOWLEDGEMENTS While much of the work in this report is technical in nature, that work can only be guided and have meaning within a human context. In this respect the Panel is deeply grateful to the large numbers of people who freely gave their time and provided the Panel with the benefit of their experience and knowledge. The Panel would like to acknowledge the work of David Faurschou and Marr Consulting, the participation of municipal governments, First Nations, producer associations, provincial staff, those people who provided excellent advice at the Panel’s roundtable sessions and the many members of the public who took the time to attend open house sessions. The Panel also thanks the staff of the department for providing access to historical documents and technical support, and for attending the open house sessions. 4 - Provincial Flood Control Infrastructure TABLE OF CONTENTS 1 Flood Control Infrastructure Matters . .9 2 Terms of Reference and Approach .....................................13 2.1 Review Process .................................................14 2.2 Public Engagement. 15 2.3 Presentation of this Report .........................................15 3 Manitoba’s Flood Control System ......................................17 3.1 Diking ..................................................19 3.2 Flood Control Works ..............................................19 3.3 Benefits of the System ............................................19 4 Operating Guidelines and Rules .......................................25 4.1 Operating Guidelines in Practice .....................................26 4.2 Operational Considerations . 27 5 The Red River Floodway .............................................28 5.1 Background ..................................................28 5.1.1 How the Floodway Works .
    [Show full text]
  • Regulation of Water Levels on Lake Manitoba and Along the Fairford River, Pineimuta Lake, Lake St
    Regulation of Water Levels on Lake Manitoba and along the Fairford River, Pineimuta Lake, Lake St. Martin and Dauphin River and Related Issues A Report to the Manitoba Minister of Conservation Volume 2: Main Report July 2003 The Lake Manitoba Regulation Review Advisory Committee Cover Photo: Looking west along the Fairford River from the Fairford River Water Control Structure. Lake Manitoba Regulation Review Advisory Committee, Main Report, July 2003 Table of Contents 1.0 Introduction ........................................................................................................................... 4 1.1 Background ...................................................................................................................... 4 1.2 Establishment of the Lake Manitoba Regulation Review Advisory Committee ............. 4 1.3 Terms of Reference .......................................................................................................... 5 1.4 Overview of Committee Activities .................................................................................. 5 2.0 Lake Manitoba Drainage Basin ........................................................................................... 8 2.1 General Description.......................................................................................................... 8 2.1.1 Lake Winnipegosis.................................................................................................. 10 2.1.2 Lake Manitoba .......................................................................................................
    [Show full text]
  • Optimal Operation of a Flood Control Systen a Thesis
    The University of Manitoba Optimal Operation of a Flood Control Systen by John Nairn MacKenzie A Thesis Submitted to the Faculty of Graduate Studies in Partial Fulfilment of the Requirements for the Degree of It{aster of Science Tl¡-nr+man+ l'ir¡i'l DePdL Llllu.lIL ^.Ê\JI \,-LVI-L FnoinoarinoLtlSrIrçvf rrrð WitIrIulft/võ, nn i nco l\4en i toba Arrmrcf I q7R C)PTiIIAL OPEIIAÏIÛN OT A FLOOD CÛNTRC]L SYSÏËi4 BY JOHN I.IÄIRÎ''J I.4¡CKEI{Z] E A clissertation submiÈted to tåte Facr*lty of Cr*ci".¡aÉe Stuse.åies of' tlre University oá' Munitoba ire partLrl f'uifilln'le¡rt ol' t!re requle'ernemts ol'tlre clegrce ot IIAST TR OF S C I ENC E o,ig78 Fernrissio¡r hus bec¡r gnunted Ëo the t-l¡ì$l,AÊLV ûF Te!U U¡{l\¡¡-:F¿- S¡TV Ol.' h{.4þ]lTO!3"4 tr¡ lenei q¡r s¿:l! copies oü t!¡is cåÈ*;ertati{!r¡" 8o the N,4TltNAL [.N8¡4,ARY ûFr {lA"l\Ai}A to l¡riar¡:*'ilrsr tl¡ls ciissertafio¡r and tr: lend or sell copies of the felnr, und {,JNl'VUåì,5åTY h{lCfì,OFlLh{S tr: pubiish i¡¡r ahsåraet of this rJissert¿¡f ion. The ar¡thor re$erve$ otå:cr publ!c¿¡Èir¡¡r rights, ¿¡¡rJ ¡"¡either the dissertation ncr exÉensive cxtri¡cfs fr¡:nr it mluy h*: gx'int*d eir otl¡er- wise repi:oeíLlced evithout t !¡c uuf l¡o¡''s writËc¡r 3:cnrr ieslr.xr" ACI$IOWLEDffiIvE\TS I would like to e4press my appTeciation to my advisor, Professor G.
    [Show full text]
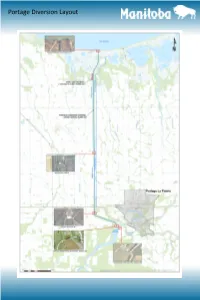
  • Portage Diversion Layout Recent and Future Projects
    Portage Diversion Layout Recent and Future Projects Assiniboine River Control Structure Public and worker safety improvements Completed in 2015 Works include fencing, signage, and safety boom Electrical and mechanical upgrades Ongoing Works include upgrades to 600V electrical distribution system, replacement of gate control system and mo- tor control center, new bulkhead gate hoist, new stand-by diesel generator fuel/piping system and new ex- terior diesel generator Portage Diversion East Outside Drain Reconstruction of 18 km of drain Completed in 2013 Replacement of culverts beneath three (3) railway crossings Completed in 2018 Recent and Future Projects Portage Diversion Outlet Structure Construction of temporary rock apron to stabilize outlet structure Completed in 2018 Conceptual Design for options to repair or replace structure Completed in 2018 Outlet structure major repair or replacement prioritized over next few years Portage Diversion Channel Removal of sedimentation within channel Completed in 2017 Groundwater/soil salinity study for the Portage Diversion Ongoing—commenced in 2016 Enhancement of East Dike north of PR 227 to address freeboard is- sues at design capacity of 25,000 cfs Proposed to commence in 2018 Multi-phase over the next couple of years Failsafe assessment and potential enhancement of West Dike to han- dle design capacity of 25,000 cfs Prioritized for future years—yet to be approved Historical Operating Guidelines Portage Diversion Operating Guidelines 1984 Red River Floodway Program of Operation Operation Objectives The Portage Diversion will be operated to meet these objectives: 1. To provide maximum benefits to the City of Winnipeg and areas along the Assiniboine River downstream of Portage la Prairie.
    [Show full text]
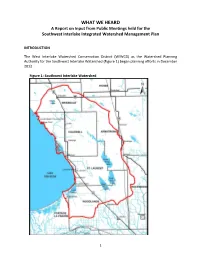
  • WHAT WE HEARD a Report on Input from Public Meetings Held for the Southwest Interlake Integrated Watershed Management Plan
    WHAT WE HEARD A Report on Input from Public Meetings held for the Southwest Interlake Integrated Watershed Management Plan INTRODUCTION The West Interlake Watershed Conservation District (WIWCD) as the Watershed Planning Authority for the Southwest Interlake Watershed (Figure 1) began planning efforts in December 2013. Figure 1: Southwest Interlake Watershed 1 The WIWCD formed a Project Management Team to guide the development of the Southwest Interlake IWMP. The Project Management Team includes: Earl Zotter (Chair) Rural Municipality of St. Laurent Jack Cruise Rural Municipality of Armstrong Henry Rosing Rural Municipality of Woodlands Brian Sigfusson Rural Municipality of Coldwell Garth Asham Rural Municipality of Portage La Prairie Neil Brandstrom Rural Municipality of Eriksdale Linda Miller West Interlake Watershed Conservation District Patrick Watson Manitoba Conservation and Water Stewardship PUBLIC MEETINGS One of the first steps in the development of the plan was to hold public meetings to discuss what residents of the watershed value within the planning area. Four public meeting were held in May and June of 2014: May 18 – Lundar, May 20 – Eriksdale, May 27 – Lake Francis, and June 7 – St. Laurent. A total of 45 watershed residents attended the meetings. The discussions from these meetings are reported in this document and will provide direction to the Project Management Team on the scope and priorities of the plan. GATHERING INPUT At each of the public meetings, participants were asked to fill in worksheets. The worksheets included questions on what people felt were the main issues in the watershed, why they felt that these were priority issues, what they valued in the watershed, how they felt the issues could and should be addressed, and a number of other questions related to watershed management.
    [Show full text]
  • Sensitivity of the Red River Basin Flood Protection System to Climate Variability and Change
    Water Resources Management 18: 89–110, 2004. 89 © 2004 Kluwer Academic Publishers. Printed in the Netherlands. Sensitivity of the Red River Basin Flood Protection System to Climate Variability and Change SLOBODAN P. SIMONOVIC1∗ and LANHAI LI2 1 Department of Civil and Environmental Engineering, Institute for Catastrophic Loss Reduction, University of Western Ontario, London, ON, Canada; 2 Department of Civil and Environmental Engineering, University of Western Ontario, London, ON, Canada, currently with ROBBERT Associates Ltd., Ottawa, ON, Canada (∗ author for correspondence, e-mail: [email protected], Fax: 519 661 4273) (Received: 16 September 2002; in final form: 8 October 2003) Abstract. An original modeling framework for assessment of climate variation and change impacts on the performance of complex flood protection system has been implemented in the evaluation of the impact of climate variability and change on the reliability, vulnerability and resiliency of the Red River Basin flood protection system (Manitoba, Canada). The modeling framework allows for an evaluation of different climate change scenarios generated by the global climate models. Temperature and precipitation are used as the main factors affecting flood flow generation. System dynamics modeling approach proved to be of great value in the development of system performance assessment model. The most important impact of climate variability and change on hydrologic processes is reflected in the change of flood patterns: flood starting time, peak value and timing. The results show increase in the annual precipitation and the annual streamflow volume in the Red River basin under the future climate change scenarios. Most of the floods generated using three different climate models had an earlier starting time and peak time.
    [Show full text]
  • Souris River Basin
    The report of the International Garrison Diversion Study Board is bound in six volumes as follows: REPORT APPENDIX A - WATER QUALITY APPENDIX B - WATER QUANTITY APPENDIX C - BIOLOGY APPENDIX D - USES APPENDIX E - ENGINEERING APPENDIX D USES INTERNATIONAL JOINTCOMMISSION December 3, 1976 December 3, 1976 International Garrison Diversion StudyBoard Ottawa, Ontario, Canada Billings, Montana,United States Gentlemen: The Uses Committee is pleasedto submit herewith its final reportin accordance with the terms ofreference given to it by the International Garrison Diversione& Study Board. H.G. Mills, CanadianCo-chairman ,,I r " i / .I ,' . -,/'+.f?&&/p&<f T .A. Sandercock, Canafim Member United States Member & yjj 9-42. D.M. Tate, Cazadian Member E.W. Stevke,United States Member (ii) SUMMARY The Uses Committeehas analyzed the impacts of GDU onmajor water uses in the Red, Assiniboine and Souris river basins andon Lakes Winnipegand Manitoba. Water Uses includedin the analysis are: munici- pal,industrial, agricultural, rural domestic, recreational, fish and wildlife, andother. The analysisof GDU impacts is confined to usesin Canada.The effects upon theseimpacts of variousalternatives andmodi- ficationsto the authorized GDU project were alsoanalysed. The following sections summarize theresults of the Uses Committee'sanalysis. (a)Municipal Use (1) Increasedcosts of municipal water supplytreatment: Deteriorated water quality will require, as a minimum measure,that currentlyinstalled or planned water treatmentplants be operated at peakefficiency, producing the best quality of water ofwhich they are capable.This measure represents an increased cost of $59,000 annually. Constituentssuch as nitrates, sulfates andsodium would remain at post- GDU levels since reduction of theseparameters is beyond the capability ofcurrent treatment facilities.
    [Show full text]
  • And Along the Fairford River, Pineimuta Lake, Lake St
    Lake Manitoba Regulation Review Advisory Committee Regulation of Water Levels on Lake Manitoba and along the Fairford River, Pineimuta Lake, Lake St. Martin and Dauphin River and Related Issues A Report to the Manitoba Minister of Conservation Volume 1 Summary Report July 2003 The Lake Manitoba Regulation Review Advisory Committee Summary Report, July 2003 Lake Manitoba Regulation Review Advisory Committee Regulation of Water Levels on Lake Manitoba and along the Fairford River, Pineimuta Lake, Lake St. Martin and Dauphin River and Related Issues A Report to the Manitoba Minister of Conservation Volume 1 Summary Report July 2003 The Lake Manitoba Regulation Review Advisory Committee Cover Photo: Looking west along the Fairford River from the Fairford River Water Control Structure. Summary Report, July 2003 Lake Manitoba Regulation Review Advisory Committee Executive Summary The Lake Manitoba Regulation Review Advisory Committee was appointed in 2001, following complaints to the Minister of Conservation with respect to relatively high water levels on Lake Manitoba. The Terms of Reference developed to guide the Lake Manitoba Regulation Review Advisory Committee are as follows: Determine the most acceptable and practicable range of regulation within which the levels of Lake Manitoba might be controlled; Decide if it is practicable and desirable to maintain the lake at certain levels during different seasons of the year, and from year to year, and if so recom- mend specific levels or range of levels; Determine the best course of action for water levels along the Fairford River, Lake Pineimuta, Lake St. Martin and the Dauphin River, including the best course of action with respect to the operation of the Fairford Dam; and, Examine existing data with respect to the present water quality of Lake Mani- toba and compare to historical water quality.
    [Show full text]