DOCSLIB.ORG

The Interstellar Medium- Overview IV Astronomy 216 Spring 2005

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Interstellar Medium- Overview IV Astronomy 216 Spring 2005 The Interstellar Medium- Overview IV Astronomy 216 Spring 2005 James Graham University of California, Berkeley The Molecular Milky Way AY 216 2 Local Star Forming Regions l Much of our knowledge of star formation comes from a few nearby regions • Taurus-Auriga & Perseus + Low mass (solar type stars) + 150 pc • Orion + Massive stars (OB stars) in Orion + 500 pc l How representative are these regions of the Galaxy as a whole? AY 216 3 Ophiuchus Wilking et al. 1987 AJ 94 106 CO Andre PP IV AY 216 4 Orion + CS cores > 200 M§ & Stellar clusters (Lada 1992 ApJL 393 25) AY 216 5 Conditions for Collapse l Supersonic motions are observed in molecular clouds • Approach thermal line widths on small scales l If cloud cores make stars, then they must be gravitationally bound • For thermal support GM/R ~ c2 = kT/µm c is the sound speed and µ ≈ 2.3 is the mean molecular R ≈ 0.1 (M / M§) (10 K / T) pc AY 216 6 Magnetic Fields l 850 µm polarimetry toward B1 shows polarized continuum Matthews & Wilson 2002 emission • Aligned grains and hence a component of the magnetic field in the plane of the sky • No correlation between the polarization angles measured ApJ in optical polarimetry. 574 822 l The polarized emission from the interior is consistent with with OH Zeeman data if the total uniform field strength is ~ 30 µG AY 216 7 Molecular Cloud Cores Myers et al. 1991 ApJ 376 561 AY 216 8 Fragmentation & Collapse: I l Jeans instability—the dispersion relation for a perturbation dr ~ ei(wt - kx) is 2 2 2 2 2 2 w = c (k - kJ ), kJ = 4"Gr0/c 2 2 • k - kJ < 0 makes w imaginary • Exponential growth when k < kJ • Growth rate, -iw, increases monotonically with decreasing k + Longest wavelength perturbations (largest mass) grow fastest + Fastest collapse of the largest scales suggests fragmentation unlikely (Larson 1985 MNRAS 214 379) AY 216 9 Fragmentation & Collapse: II l The Virial Theorem—dot Euler equation with r and integrate over V r r 0 3P dV r dm P r dS = Ú - Ú ( ⋅ —f ) - Ú ext ⋅ V V S 3 GM 2 0 = 3c 2 M - - 4pR3P 5 R ext Pext † V AY 216 10 Virial Theorem l There is a minimum radius where the cloud can no longer support itself against gravity 3c 2 M 3 GM 2 P = - 4pR3 20 pR4 P P~1/R3 † R Rmax l Beyond the critical point self-gravity decreases R without any help from P l Equilibria states which require P to decrease with decreasing R are unstable AY 216 11 Stable and Unstable Virial Equlibria l For a given P there are two equilibria P A B R Rmax l Squeeze the cloud at • Requires more pressure to confine it at its new radius • Re-expand (stable) l Squeeze the cloud at A • Requires less pressure to confine it AY 216 • Contract (unstable) 12 Non-Thermal Pressure l Magnetic fields are difficult to measure in cloud cores • OH absorption measurements are Stokes I Crutcher difficult because of the small chance 1667 MHz of a background radio source 1665 MHz l Single measurement of |B| cos q ≈ - 1993 19 ± 4 µG towards B1 ApJ 3 -3 • OH probes nH ≈ 10 cm Stokes V 2 5 -3 407 175 l B /8" ~ 3 x 10 K cm • Comparable to the thermal pressure of a 10 K core with n ~ 104 cm-3 AY 216 13 Magnetized Cloud l Assume a uniformly magnetized cloud 3 GM 2 1 0 = 3c 2 M - + R3B2 - 4pR3P 5 R 3 Magnetic flux is F = pR2B = const. for a good conductor • Gravitational and magnetic terms ~ 1/R i.e., they remain in constant proportion † AY 216 14 Protostellar Accretion 3 l dM/dt ~ c /G l Mo = 0.01 M§ Ro= 3.5 R§ -5 -1 l dM/dt = 10 M§ yr for 105 yr • Accretion shut off at 1 M§ 1 R • Gas photosphere cools § at constant R for ~ 1 day 100 R • Loiters for ~ 3000 yr on 5 R 1500 R § 2 the D main-sequence § § • Followed by Hayashi contraction AY 216 15 T Tauri Stars & Herbig Ae/Be Stars l T Tauri stars have long PMS evolution HAeBes • 10-100 Myr l Herbig Ae/Be stars are 2-10 M§ • tPMS < 10 Myr l For M > 5 M§ there is no PMS phase • Birthline indicates approximate location where YSOs become visible T Tauri AY 216 16 The Four Stages of Star Formation 1 2 4 Shu et al. (1987 3 ARAA 25 23) AY 216 17 SED Classification Class I Infall with simultaneous bipolar outflow Class II Visible T Tauri stars with disks & winds Class III Circumstellar material accreted or dissipated, leaving a pre-main-sequence star, possibly with planets AY 216 18 Inside-Out Collapse in B335 Choi et al. 1995 ApJ 448 742 AY 216 19 The HH 211 Outflow • 1.3 mm continuum • Circumstellar disk • 12CO 2 – 1 • Molecular outflow • Top: |v| < 10 km/s • Bottom: |v| > 10 km/s • H2 2.12 µm • Shocks • Gueth & Guilloteau 1999 A&A 343 571 AY 216 20 Evolving Circumstellar Environment l Debris disk studies suggest that the quantity of circumstellar material declines rapidly with age: M µ t -2 AY 216 21 OB stars in Orion M42 l 450 pc l t < 1-2 Myr l 3500 stars within 2.5 pc radius • 0.1 - 50 M§ • 900 M§ l A few O stars • Lots of low mass stars too (Hillenbrand 1997 AJ 113 1733) AY 216 22 High Mass Stars l Evolutionary time scales for OB stars are << for low-mass stars • OB stars modify their environment soon after a stellar core has formed since their Kelvin-Helmholtz time scale 2 tKH = E/L ~ GM /LR < 104 yrs for an O star l Core H-burning begins before accretion of matter from the surrounding protostellar envelope stops l When the protostar reaches the ZAMS, it begins producing appreciable UV flux and (possibly) a strong wind modifying the surrounding conditions, structure, & chemistry l The new OB star ionizes its surroundings, giving rise to a small region of ionized gas, usually referred as the ultracompact HII (UCHII) region phase • UCHII regions have diameters < 0.05 pc • Compact HII regions have sizes in the range 0.05-0.5 pc AY 216 23 Properties of Massive Stars l Massive stars = O & B stars l Massive stars are OB stars which ionize HII regions Spectral Mass MV Teff log10 -1 Type M§ K (Q / g s ) O5 60 -5.6 48,000 49.7 O8 23 -5.2 33,500 48.6 B0 18 -4.4 30,000 47.7 AY 216 24 Dense Gas & Massive Stars l The hallmark of newly formed OB stars are NH compact and ultra- 3 compact HII regions UCHII l Intimately associated with warm and dense regions of molecular gas • G9.62+0.19 + UC HII region + NH3 hot core (dashed) + 1.3 cm continuum emission (solid) + H2O (p) & OH (o) masers (Kurtz PPIV) AY 216 25 Morphology of Compact HII Regions l High angular resolution Bipolar radio continuum Shell observations show a variety of morphologies • UC HII regions in radio continuum • Shell source G45.07+0.13 (Turner & Matthews 1984) • Bipolar source NGC 7538 (Campbell 1984). Cometary • Cometary source G34.3+0.15 (Gaume et al. 1994). AY 216 26 Statistics of UCHII Regions l Why do we see so many UC HII regions? l IRAS point source catalog & a far-IR color criterion selects UC HII • Wood & Churchwell (1989) counted 1650 Galactic UC HII • If these objects have physical parameters similar to a much smaller number of radio-observed UC HII then + R ~ 0.05 pc 48 -1 + NU ~ 4 x 10 s 5 -3 + n0 ~ 10 cm • Dynamical ages are typically ~ 5000 yr -1 l Implies ~1650/5000 = 0.3 O stars yr l Considerably larger than that estimated from other means -1 • Typical estimates give 0.82 M§ yr (10 < M/M§ < 60) (Güsten & Mezger 1983 or Downes 1987) -1 • An IMF-weighted of <MOB> 23 M§ implies ~ 0.04 O stars yr • 10 times smaller than that derived from UC HII regions AY 216 27 Champagne Flows l “Champagne flow” or blister models assume that the massive star is born in a medium with large density gradients • The star evacuates a cavity of ionized gas • At the boundary of the cloud the ionized cavity breaks out creating a flow of gas away from the cloud due to the pressure gradient between respectively the cloud and the ambient ISM AY 216 28 Bow Shocks l Cometary HII regions may be stellar wind bow shocks of an ionizing star moving supersonically through a molecular cloud (Van Buren et al. 1990; MacLow et al. 1991) • Bow shocks explain details of the morphology + Limb brightening + Emission pinches back down to the symmetry axis u Not easily explained within the champagne models AY 216 29 30 Hollenbach et al. (1994 ApJ 428 654) isks D * 2 c GM = g r hotoevaporating † P AY 216 A High-Mass Protostar with a Massive Rotating Disk l The high-mass Class 0 protostar NGC 7538S has a massive rotating disk and outflow 13 l Resolved with the BIMA in the 3.4 mm continuum and in H CN • Nearly edge-on and has a size of 30,000 AU • Outflow perpendicular to the rotating disk is mapped in SiO and HCO+ 13 l H CN velocity gradient is consistent with Keplerian rotation orbiting a ~ 40 M§ central object 4 l The mass of the continuum "disk" is 100 M § and has a luminosity of 10 L§ 13 l H CN gives 400 M§ for the rotating disk and of 1000 M§ for the extended envelope + H13CN contours/3.4 mm continuum HCO outflow AY 216 31.
Load more

Recommended publications
  • Lecture Star Formation 2. Pptx.Pptx
    Lecture Star Formaon History 2 Prof. George F. Smoot Star Formaon 2 1 Star Formaon, H II Regions, and the Interstellar Medium Star Formaon 2 2 Introduc-on • Baryonic maer: Maer composed of protons and neutrons • Interstellar Medium (ISM): Consists of molecular, atomic, and ionized gas with large ranges of densi-es and temperatures, as well as dust • New Stars form from molecular, gas-phase maer • ISM releases stellar energy by means of physical processes that are dis-nct from star and stellar formaon Star Formaon 2 3 What to Expect • Focus on the ISM in star-forming regions • Briefly survey star forming environments • Proper-es of young stellar populaons • Physical processes that operate in the ISM around newly formed stars and the observable conseQuences of those processes Star Formaon 2 4 5.1 Cloud Collapse and Star Formaon • Stars form in molecular clouds, which are one component of ISM • Clouds are randomly shaped agglomeraons composed of molecular hydrogen 2 5 • Typical mass of 10 -10 MSun • Sizes of hundreds of parsecs • Densies of 108-1010 m-3 (mostly hydrogen) • Temperature between ~ 10–100 K Star Formaon 2 5 Molecular Clouds • Clouds are largest, most massive, gravitaonally bound objects in ISM • Densi-es of clouds are among highest found in ISM • Nearest giant molecular clouds are in the Orion star- forming region, ~500 pc away Star Formaon 2 6 7 Cloud in Orion Molecular hp://www.outerspaceuniverse.org/media/orion-molecular-cloud.jpg Star Formaon 2 Molecular Clouds • Mean mass density in stars are ~103 kg/m3 and par-cle density
    [Show full text]
  • Planet Formation
    Planet Formation A Major Qualifying Project Report: Submitted to the Faculty of Worcester Polytechnic Institute In partial fulfillment of the requirements for the Degree of Bachelor of Science By Peter Dowling Advised by Professor Mayer Humi Peter Dowling Table of Contents Abstract .......................................................................................................................................................... 4 Executive Summary ........................................................................................................................................ 5 Introduction ................................................................................................................................................... 7 Background .................................................................................................................................................... 7 Stellar Formation ........................................................................................................................................ 8 Jeans Instability ...................................................................................................................................... 8 History of Solar System Formation Theories............................................................................................ 10 Tidal Theory .......................................................................................................................................... 11 The Chamberlin-Moulton model .........................................................................................................
    [Show full text]
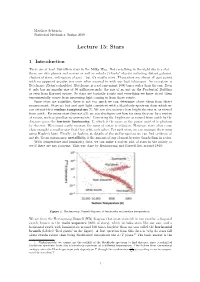
  • Lecture 15: Stars
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 15: Stars 1 Introduction There are at least 100 billion stars in the Milky Way. Not everything in the night sky is a star there are also planets and moons as well as nebula (cloudy objects including distant galaxies, clusters of stars, and regions of gas) but it's mostly stars. These stars are almost all just points with no apparent angular size even when zoomed in with our best telescopes. An exception is Betelgeuse (Orion's shoulder). Betelgeuse is a red supergiant 1000 times wider than the sun. Even it only has an angular size of 50 milliarcseconds: the size of an ant on the Prudential Building as seen from Harvard square. So stars are basically points and everything we know about them experimentally comes from measuring light coming in from those points. Since stars are pointlike, there is not too much we can determine about them from direct measurement. Stars are hot and emit light consistent with a blackbody spectrum from which we can extract their surface temperature Ts. We can also measure how bright the star is, as viewed from earth . For many stars (but not all), we can also gure out how far away they are by a variety of means, such as parallax measurements.1 Correcting the brightness as viewed from earth by the distance gives the intrinsic luminosity, L, which is the same as the power emitted in photons by the star. We cannot easily measure the mass of a star in isolation. However, stars often come close enough to another star that they orbit each other.
    [Show full text]
  • Lecture 22 Stability of Molecular Clouds
    Lecture 22 Stability of Molecular Clouds 1. Stability of Cloud Cores 2. Collapse and Fragmentation of Clouds 3. Applying the Virial Theorem References • Myers, “Physical Conditions in Molecular Clouds” in Origins of Stars & Planetary Systems eds. Lada & Kylafis http://www.cfa.harvard.edu/events/1999crete • For the Virial Theorem: Shu II, Ch. 12 & Stahler, Appendix D ay216 1 1. Stability of Molecular Cloud Cores Summary of molecular cloud core properties (Lec. 21) relating to virial equilibrium: 1. Location of star formation 2. Elongated (aspect ratio ~ 2:1) 3. Internal dynamics dominated by thermal or by turbulent motion 4. Often in approximate virial equilibrium 5. Temperature: T ~ 5 – 30 K 6. Size: R ~ 0.1 pc -7 7. Ionization fraction: xe ~ 10 8. Size-line width relation* R ~ p , p = 0.5 ± 0.2 9. Mass spectrum similar to GMCs. * Does not apply always apply, e.g. the Pipe Nebula (Lada et al. 2008). ay216 2 Non-Thermal vs. Thermal Core Line Widths turbulent thermal Turbulent cores are warmer than quiescent cores ay216 3 Consistency of Cores and Virial Equilibrium Gravitational energy per unit mass vs. Column Density v2/R Models of virial equilibrium (funny symbols) easily fit the observations (solid circles [NH3] and squares [C18O]). Recall that the linewidth-size relation implies that both the ordinate and abscissa are ~ constant. Myers’ data plot illustrates this result, at least approximately for a diverse sample of cores. N For pure thermal support, GM/R ~ kT/m, (m = 2.3 mH), or R 0.1 (M / M) (10 K / T) pc. ay216 4 First Consideration of Core Stability • Virial equilibrium seems to be an appropriate state from which cores proceed to make stars.
    [Show full text]
  • Lecture 3 Properties and Evolution of Molecular Clouds
    Lecture 3 Properties and Evolution of Molecular Clouds Spitzer space telescope image of Snake molecular cloud (IRDC G11.11-0.11 From slide from Annie Hughes Review COt in clouds HI: Atomic Hydrogen http://www.atnf.csiro.au/research/LVmeeting/magsys_pres/ ahughes_MagCloudsWorkshop.pdf The Galaxy in CO The CfA CO Survey (488,000 spectra 7’ resolution II I IV III Quadrants http://cfa-www.harvard.edu/mmw/MilkyWayinMolClouds.html 2MASS Near-IR Survey The Orion Giant Molecular Cloud Complex Total mass 200,000 Msun 4 CO map of Wilson et al. (2005) overlaid on image of Orion Molecular Cloud Properties -4 Composition: H2, He, dust (1% mass), CO (10 by number), and many other molecules with low abundances. Sizes: 10-100 pc Masses: 10 to 106 Msun. Most of the molecular gas mass in galaxies is found in the more massive clouds. Average Density: 100 cm-3 Lifetimes: < 10 Myr - we will discuss this when we discuss the lifetime problem. Issue: it is hard to separate individual clouds - not well defined. Cloud Mass Function dN/dlog(m) = kM-0.81 6 Mupper = 5.8 x 10 Msun dN/dlog(m) = kM-0.67 6 Mupper = 5.8 x 10 Msun Mass is weighted toward the most massive clouds Williams & McKee 1997 ApJ 476, 166. Larson’s Laws In 1981, Richard Larson wrote a paper titled: Turbulence and Star Formation in Molecular Clouds (MNRAS 1984, 809) Used tabulation of molecular cloud properties to discover to empirical laws based on the cloud length L (max. projected length) 0.38 Size-linewidth relationship: σv (km s-1) = 1.10 L (pc) 0.5 more recent values give σv = const L Density-radius relationship: <n(H2)>(cm-3) =3400 L -1.1 (pc) 22 -2 more recent interpretation is that N(H2) =1 x 10 cm Size-Linewidth Relationship Solomon 1987 ApJ 319, 730 Are Clouds Bound? Are Clouds Bound? Are Clouds Bound? Larson 1981 Virial Bound Note: σ is 3-D velocity distribution Using Galactic Ring Data Virial Bound Note: alpha may be underestimated Heyer et al.
    [Show full text]
  • A620 Star Formation
    NEW TOPIC- Star Formation- Ch 9 MBW Please read 9.1-9.4 for background • One of the most important processes for galaxy formation and evolution • Big questions – When and how does star formation occur ? – How is it related to the evolution of galaxy properties? – What are the physical processes that drive star formation ? • star formation occurs (at least in spirals at low z) almost exclusively associated with molecular clouds • what is the rate at which stars form in this cloud • what mass fraction of the cloud forms stars • what controls the IMF? • is high redshift star formation the same sort of process as at low z? Star Formation in Spirals • This is an enormous subject- lots of recent work (see Star Formation in the Milky Way and Nearby Galaxies Kennicutt, Jr. and Evans ARA&A Vol. 50 (2012): 531) • Observations of nearby galaxies – over a broad range of galactic environments and metallicities, star formation occurs only in the molecular phase of the interstellar medium (ISM). e.g. Star formation is strongly linked to the molecular clouds – Theoretical models show that this is due to the relationship between chemical phase, shielding, and temperature. • Interstellar gas converts from atomic to molecular only in regions that are well shielded from interstellar ultraviolet (UV) photons, and since UV photons are also the dominant source of interstellar heating, only in these shielded regions does the gas become cold enough to be subject to Jeans instability (Krumholz 2012) • In the MW and other well studied nearby galaxies SF occurs mostly in (Giant molecular clouds (GMCs, which are predominantly molecular, gravitationally 5 6 bound clouds with typical masses ~ 10 – 10 M )- but GMC formation is a local, not a global process • Observationally one uses CO as a tracer for H2 (not perfect but the best we have right now).
    [Show full text]
  • 198Oapj. . .238. .158N the Astrophysical Journal, 238:158-174
    .158N .238. The Astrophysical Journal, 238:158-174, 1980 May 15 . © 1980. The American Astronomical Society. All rights reserved. Printed in U.S.A. 198OApJ. CLUMPY MOLECULAR CLOUDS: A DYNAMIC MODEL SELF-CONSISTENTLY REGULATED BY T TAURI STAR FORMATION Colin Norman Huygens Laboratory, University of Leiden AND Joseph Silk Department of Astronomy, University of California, Berkeley Received 1978 December 11; accepted 1979 October 31 ABSTRACT A new model is proposed which can account for the longevity, energetics, and dynamical structure of dark molecular clouds. It seems clear that the kinetic and gravitational energy in macroscopic cloud motions cannot account for the energetics of many molecular clouds. A stellar energy source must evidently be tapped, and infrared observations indicate that one cannot utilize massive stars in dark clouds. Recent observations of a high space density of T Tauri stars in some dark clouds provide the basis for our assertion that high-velocity winds from these low-mass pre- main-sequence stars provide a continuous dynamic input into molecular clouds. The T Tauri winds sweep up shells of gas, the intersections or collisions of which form dense clumps embedded in a more rarefied interclump medium. Observations constrain the clumps to be ram-pressure confined, but at the relatively low Mach numbers, continuous leakage occurs. This mass input into the interclump medium leads to the existence of two phases ; a dense, cold phase (clumps of density ~ 104-105 cm-3 and temperature ~ 10 K) and a warm, more diffuse, interclump medium (ICM, of density ~ 103-104 cm-3 and temperature ~30 K). Clump collisions lead to coalescence, and the evolution of the mass spectrum of clumps is studied.
    [Show full text]
  • Jeans Instability of Dissipative Self-Gravitating Bose–Einstein Condensates with Repulsive Or Attractive Self-Interaction: Application to Dark Matter
    universe Article Jeans Instability of Dissipative Self-Gravitating Bose–Einstein Condensates with Repulsive or Attractive Self-Interaction: Application to Dark Matter Pierre-Henri Chavanis Laboratoire de Physique Théorique, Université de Toulouse, CNRS, UPS, 31062 Toulouse, France; [email protected] Received: 13 October 2020; Accepted: 15 November 2020; Published: 27 November 2020 Abstract: We study the Jeans instability of an infinite homogeneous dissipative self-gravitating Bose–Einstein condensate described by generalized Gross–Pitaevskii–Poisson equations [Chavanis, P.H. Eur. Phys. J. Plus 2017, 132, 248]. This problem has applications in relation to the formation of dark matter halos in cosmology. We consider the case of a static and an expanding universe. We take into account an arbitrary form of repulsive or attractive self-interaction between the bosons (an attractive self-interaction being particularly relevant for the axion). We consider both gravitational and hydrodynamical (tachyonic) instabilities and determine the maximum growth rate of the instability and the corresponding wave number. We study how they depend on the scattering length of the bosons (or more generally on the squared speed of sound) and on the friction coefficient. Previously obtained results (notably in the dissipationless case) are recovered in particular limits of our study. Keywords: Jeans instability; self-gravitating Bose-Einstein condensates; dark matter 1. Introduction Cosmological observations have revealed that baryonic (visible) matter represents only 5% of the content of the Universe. The rest of the Universe is invisible, being made of 25% dark matter (DM) and 70% dark energy (DE) [1]. DE has been introduced to explain why the expansion of the universe is presently accelerating.
    [Show full text]
  • Theory of Star Formation
    ANRV320-AA45-13 ARI 16 June 2007 20:24 V I E E W R S First published online as a Review in Advance on June 25, 2007 I E N C N A D V A Theory of Star Formation Christopher F. McKee1 and Eve C. Ostriker2 1Departments of Physics and Astronomy, University of California, Berkeley, California 94720; email: [email protected] 2Department of Astronomy, University of Maryland, College Park, Maryland 20742; email: [email protected] Annu. Rev. Astron. Astrophys. 2007. 45:565–686 Key Words The Annual Review of Astrophysics is online at accretion, galaxies, giant molecular clouds, gravitational collapse, astro.annualreviews.org HII regions, initial mass function, interstellar medium, jets and This article’s doi: outflows, magnetohydrodynamics, protostars, star clusters, 10.1146/annurev.astro.45.051806.110602 turbulence Copyright c 2007 by Annual Reviews. All rights reserved Abstract 0066-4146/07/0922-0565$20.00 We review current understanding of star formation, outlining an overall theoretical framework and the observations that motivate it. A conception of star formation has emerged in which turbulence plays a dual role, both creating overdensities to initiate gravita- tional contraction or collapse, and countering the effects of gravity in these overdense regions. The key dynamical processes involved in star formation—turbulence, magnetic fields, and self-gravity— are highly nonlinear and multidimensional. Physical arguments are used to identify and explain the features and scalings involved in star formation, and results from numerical simulations are used to quantify these effects. We divide star formation into large-scale and by University of California - Berkeley on 07/26/07.
    [Show full text]
  • Arxiv:0907.0434V2 [Gr-Qc] 7 Jul 2009 Ihs Ymti Akrud Nfc,Cnieigtema Ene Mean the Considering Fact, in I.E
    THE JEANS INSTABILITY IN PRESENCE OF VISCOUS EFFECTS Nakia Carlevaro a, b and Giovanni Montani b, c, d, e aDepartment of Physics, Polo Scientifico – Universit`adegli Studi di Firenze, INFN – Section of Florence, Via G. Sansone, 1 (50019), Sesto Fiorentino (FI), Italy bICRA – International Center for Relativistic Astrophysics, c/o Dep. of Physics - “Sapienza” Universit`adi Roma c Department of Physics - “Sapienza” Universit`adi Roma, Piazza A. Moro, 5 (00185), Rome, Italy dENEA – C.R. Frascati (Department F.P.N.), Via Enrico Fermi, 45 (00044), Frascati (Rome), Italy e ICRANet – C. C. Pescara, Piazzale della Repubblica, 10 (65100), Pescara, Italy [email protected] [email protected] Abstract: An analysis of the gravitational instability in presence of dissipa- tive effects is addressed. In particular, the standard Jeans Mechanism and the generalization in treating the Universe expansion are both analyzed when bulk viscosity affects the first-order Newtonian dynamics. As results, the perturbation evolution is founded to be damped by dissipative processes and the top-down mechanism of structure fragmentation is suppressed. In such a scheme, the value of the Jeans Mass remains unchanged also in presence of viscosity. 1 Introduction The Cosmological Standard Model [1] well describes many parts of the Universe evolution and it takes into account the Friedmann-Lemaˆıtre-Robertson-Walker (FLRW) metric as the highest symmetric background. In fact, considering the mean energy-density at big scales, arXiv:0907.0434v2 [gr-qc] 7 Jul 2009 i.e., greater than 100 Mpc, it tends to an homogeneous distribution. On the other hand, the Universe observation at small scales shows a very inhomogeneous and anisotropic matter- and energy-distribution.
    [Show full text]
  • Jeans Instability in the Expanding Universe
    A Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 16 February 2018 (MN L TEX style file v2.2) Jeans Instability in the expanding Universe. 16 February 2018 1 GAS PROPERTIES Here we consider fluctuations in baryons and waves shorter than the distance to the horizon dH (t). We deal with ideal fluid with pressure P . For non-expanding medium the Jeans length can be estimated by equating the time needed for a wave to travel across an object tcross = lJ /vs to the object’s free fall time tdynamic =1/√4πGρ. The critical wavelength is defined by the sound speed vs and density of matter ρ: v l s . (1) J ≈ √4πGρ A better way of solving the problem is to find the critical wavelength using the dispersion relation for waves propogating in a homogeneous gas with given density and temperature. The answer gives the critical wave-length lJ that separates two regimes. Waves shorter than than lJ oscillate and their amplitude does not grow. Waves longer than lJ experience growth. Sound speed in gas is dP P v2 = = γ , (2) s dρ ρ For normal ideal gas the pressure is defined by the random motions of atoms, ions and electrons: 2 γkT vs = , (3) µmH where P = nkT, ρ = µnmH , (4) and γ is the ratio of heat capacities γ = cp/cv. It is equal to γ =5/3 for mono-atomic gas. µ is the molecular weight (depends on the ionization state). mH mass of a proton. k is the Boltzmann constant. Before the recombination (z 1100) the gas is ionized and its pressure is provided ≈ c 0000 RAS 2 mostly by the photons through Thompson scattering, not by random motions of atoms and electrons: 2 ρgaskT ργ c 2 4 P = + , ργ c = σT .
    [Show full text]
  • Quasi-Linear Theory of the Jeans Instability in Disk-Shaped Galaxies
    A&A 383, 338–351 (2002) Astronomy DOI: 10.1051/0004-6361:20011713 & c ESO 2002 Astrophysics Quasi-linear theory of the Jeans instability in disk-shaped galaxies E. Griv1, M. Gedalin1,andC.Yuan2 1 Department of Physics, Ben-Gurion University of the Negev, PO Box 653, Beer-Sheva 84105, Israel 2 Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), PO Box 23, Taipei 106, Taiwan Received 4 September 2001 / Accepted 29 November 2001 Abstract. We analyse the reaction between almost aperiodically growing Jeans-unstable gravity perturbations and stars of a rotating and spatially inhomogeneous disk of flat galaxies. A mathematical formalism in the approx- imation of weak turbulence (a quasi-linearization of the Boltzmann collisionless kinetic equation) is developed. A diffusion equation in configuration space is derived which describes the change in the main body of equilibrium distribution of stars. The distortion in phase space resulting from such a wave–star interaction is studied. The theory, applied to the Solar neighborhood, accounts for the observed Schwarzschild shape of the velocity ellipsoid, the increase in the random stellar velocities with age, and the essential radial migration of the Sun from its birth-place in the inner part of the Galaxy outwards during its lifetime. Key words. galaxies: kinematics and dynamics – galaxies: structure – waves – instabilities 1. Introduction investigation by studying the nonlinear effects. The prob- lem is formulated in the same way as in plasma kinetic The theory of spiral structure of rotationally
    [Show full text]