The Rhythm That Conquered the World: What Makes a “Good” Rhythm Good?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Beyond Salsa Bass the Cuban Timba Revolution
BEYOND SALSA BASS THE CUBAN TIMBA REVOLUTION VOLUME 1 • FOR BEGINNERS FROM CHANGÜÍ TO SON MONTUNO KEVIN MOORE audio and video companion products: www.beyondsalsa.info cover photo: Jiovanni Cofiño’s bass – 2013 – photo by Tom Ehrlich REVISION 1.0 ©2013 BY KEVIN MOORE SANTA CRUZ, CA ALL RIGHTS RESERVED No part of this publication may be reproduced in whole or in part, or stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopy, recording or otherwise, without written permission of the author. ISBN‐10: 1482729369 ISBN‐13/EAN‐13: 978‐148279368 H www.beyondsalsa.info H H www.timba.com/users/7H H [email protected] 2 Table of Contents Introduction to the Beyond Salsa Bass Series...................................................................................... 11 Corresponding Bass Tumbaos for Beyond Salsa Piano .................................................................... 12 Introduction to Volume 1..................................................................................................................... 13 What is a bass tumbao? ................................................................................................................... 13 Sidebar: Tumbao Length .................................................................................................................... 1 Difficulty Levels ................................................................................................................................ 14 Fingering.......................................................................................................................................... -

Song Artist 25 Or 6 to 4 Chicago 5 Years Time Noah and the Whale A
A B 1 Song Artist 2 25 or 6 to 4 Chicago 3 5 Years Time Noah and the Whale 4 A Horse with No Name America 5 Achy Breaky Heart Billy Ray Cyrus 6 Adelaide Old 97's 7 Adelaide 8 Africa Bamba Santana 9 Against the Wind Bob Seeger 10 Ain't to Proud to Beg The Temptations 11 All Along the W…. Dylan/ Hendrix 12 Back in Black ACDC 13 Bad Leroy Brown Jim Croce 14 Bad Moon Risin' CCR 15 Bad to the Bone George Thorogood 16 Bamboleo Gipsy Kings 17 Black Horse and… KT Tunstall 18 Born to be Wild Steelers Wheels 19 Brain Stew Green Day 20 Brown Eyed Girl Van Morrison 21 Chasing Cars Snow Patrol 22 Cheesburger in Para… Jimmy Buffett 23 Clocks Coldplay 24 Close to You JLS 25 Close to You 26 Come as you Are Nirvana 27 Dead Flowers Rolling Stones 28 Down on the Corner CCR 29 Drift Away Dobie Gray 30 Duende Gipsy Kings 31 Dust in the Wind Kansas 32 El Condor Pasa Simon and Garfunkle 33 Every Breath You Take Sting 34 Evil Ways Santana 35 Fire Bruce Springsteen Pointer Sis.. 36 Fire and Rain James Taylor A B 37 Firework Katy Perry 38 For What it's Worth Buffalo Springfield 39 Forgiveness Collective Soul 40 Free Bird Lynyrd Skynyrd 41 Free Fallin Tom Petty 42 Give me One Reason Tracy Chapman 43 Gloria Van Morrison 44 Good Riddance Green Day 45 Have You Ever Seen… CCR 46 Heaven Los Lonely Boys 47 Hey Joe Hendrix 48 Hey Ya! Outcast 49 Honkytonk Woman Rolling Stones 50 Hotel California Eagles 51 Hotel California 52 Hotel California Eagles 53 Hotel California 54 I Won't Back Down Tom Petty 55 I'll Be Missing You Puff Daddy 56 Iko Iko Dr. -

A Musical Analysis of Afro-Cuban Batá Drumming
City University of New York (CUNY) CUNY Academic Works All Dissertations, Theses, and Capstone Projects Dissertations, Theses, and Capstone Projects 2-2019 Meaning Beyond Words: A Musical Analysis of Afro-Cuban Batá Drumming Javier Diaz The Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/2966 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] MEANING BEYOND WORDS: A MUSICAL ANALYSIS OF AFRO-CUBAN BATÁ DRUMMING by JAVIER DIAZ A dissertation submitted to the Graduate Faculty in Music in partial fulfillment of the requirements for the degree of Doctor of Musical Arts, The City University of New York 2019 2018 JAVIER DIAZ All rights reserved ii Meaning Beyond Words: A Musical Analysis of Afro-Cuban Batá Drumming by Javier Diaz This manuscript has been read and accepted for the Graduate Faculty in Music in satisfaction of the dissertation requirement for the degree of Doctor in Musical Arts. ——————————— —————————————————— Date Benjamin Lapidus Chair of Examining Committee ——————————— —————————————————— Date Norman Carey Executive Officer Supervisory Committee Peter Manuel, Advisor Janette Tilley, First Reader David Font-Navarrete, Reader THE CITY UNIVERSITY OF NEW YORK iii ABSTRACT Meaning Beyond Words: A Musical Analysis of Afro-Cuban Batá Drumming by Javier Diaz Advisor: Peter Manuel This dissertation consists of a musical analysis of Afro-Cuban batá drumming. Current scholarship focuses on ethnographic research, descriptive analysis, transcriptions, and studies on the language encoding capabilities of batá. -

The Role of Bell Patterns in West African and Afro-Caribbean Music
Braiding Rhythms: The Role of Bell Patterns in West African and Afro-Caribbean Music A Smithsonian Folkways Lesson Designed by: Jonathan Saxon* Antelope Valley College Summary: These lessons aim to demonstrate polyrhythmic elements found throughout West African and Afro-Caribbean music. Students will listen to music from Ghana, Nigeria, Cuba, and Puerto Rico to learn how this polyrhythmic tradition followed Africans to the Caribbean as a result of the transatlantic slave trade. Students will learn the rumba clave pattern, cascara pattern, and a 6/8 bell pattern. All rhythms will be accompanied by a two-step dance pattern. Suggested Grade Levels: 9–12, college/university courses Countries: Cuba, Puerto Rico, Ghana, Nigeria Regions: West Africa, the Caribbean Culture Groups: Yoruba of Nigeria, Ga of Ghana, Afro-Caribbean Genre: West African, Afro-Caribbean Instruments: Designed for classes with no access to instruments, but sticks, mambo bells, and shakers can be added Language: English Co-Curricular Areas: U.S. history, African-American history, history of Latin American and the Caribbean (also suited for non-music majors) Prerequisites: None. Objectives: Clap and sing clave rhythm Clap and sing cascara rhythm Clap and sing 6/8 bell pattern Dance two-bar phrase stepping on quarter note of each beat in 4/4 time Listen to music from Cuba, Puerto Rico, Ghana, and Nigeria Learn where Cuba, Puerto Rico, Ghana, and Nigeria are located on a map Understand that rhythmic ideas and phrases followed Africans from West Africa to the Caribbean as a result of the transatlantic slave trade * Special thanks to Dr. Marisol Berríos-Miranda and Dr. -

The Geometry of Musical Rhythm
The Geometry of Musical Rhythm Godfried Toussaint? School of Computer Science McGill University Montr´eal, Qu´ebec, Canada Dedicated to J´anos Pach on the occasion of his 50th birthday. Abstract. Musical rhythm is considered from the point of view of ge- ometry. The interaction between the two fields yields new insights into rhythm and music theory, as well as new problems for research in mathe- matics and computer science. Recent results are reviewed, and new open problems are proposed. 1 Introduction Imagine a clock which has 16 hours marked on its face instead of the usual 12. Assume that the hour and minute hands have been broken off so that only the second-hand remains. Furthermore assume that this clock is running fast so that the second-hand makes a full turn in about 2 seconds. Such a clock is illustrated in Figure 1. Now start the clock ticking at \noon" (16 O'clock) and let it keep running for ever. Finally, strike a bell at positions 16, 3, 6, 10 and 12, for a total of five strikes per clock cycle. These times are marked with a bell in Figure 1. The resulting pattern rings out a seductive rhythm which, in a short span of fifty years during the last half of the 20th century, has managed to conquer our planet. It is known around the world (mostly) as the Clave Son from Cuba. However, it is common in Africa, and probably travelled from Africa to Cuba with the slaves [65]. In Africa it is traditionally played with an iron bell. -

Beyond Salsa for Ensemble a Guide to the Modern Cuban Rhythm Section
BEYOND SALSA FOR ENSEMBLE A GUIDE TO THE MODERN CUBAN RHYTHM SECTION PIANO • BASS • CONGAS • BONGÓ • TIMBALES • DRUMS VOLUME 1 • EFECTOS KEVIN MOORE REVISION 1.0 ©2012 BY KEVIN MOORE SANTA CRUZ, CA ALL RIGHTS RESERVED No part of this publication may be reproduced in whole or in part, or stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopy, recording or otherwise, without written permission of the author. ISBN‐10: 146817486X ISBN‐13/EAN‐13: 978‐1468174861 www.timba.com/ensemble www.timba.com/piano www.timba.com/clave www.timba.com/audio www.timba.com/percussion www.timba.com/users/7 [email protected] cover design: Kris Förster based on photos by: Tom Ehrlich photo subjects (clockwise, starting with drummer): Bombón Reyes, Daymar Guerra, Miguelito Escuriola, Pupy Pedroso, Francisco Oropesa, Duniesky Baretto Table of Contents Introduction to the Beyond Salsa Series .............................................................................................. 12 Beyond Salsa: The Central Premise .................................................................................................. 12 How the Series is Organized and Sold .......................................................................................... 12 Book ......................................................................................................................................... 12 Audio ....................................................................................................................................... -

BO DIDDLEY's UNCONVENTIONAL 1950'S SOUND and ITS
BO DIDDLEY’S UNCONVENTIONAL 1950’s SOUND AND ITS ANTICIPATION OF HIP HOP OVERVIEW ESSENTIAL QUESTION How were Bo Diddley’s recordings an anomaly in relation to 1950s Pop music, and how is his rhythm-driven sound and self-presentation a precursor to Hip Hop style? OVERVIEW From his first appearance on the Billboard R&B chart in 1955 and continuing over his five- decade career, Bo Diddley has been celebrated for the rhythm-driven, percussive sound of his ensemble, at the center of which was Diddley’s guitar playing. If by the Rock era the guitar solo became a symbolic centerpiece in recordings and performances, Diddley’s emphasis was always on the rhythm guitar. His approach didn’t revolve around the single- and double-note leads that came to dominate the music. Instead, Bo Diddley pioneered a sound that involved every member of his combo playing with a percussive sensibility. Rhythm was emphasized over melody, with a vocal style that often approximated Rap set against that rhythmic backdrop. Earlier even than James Brown, Diddley inadvertently pointed to a Hip Hop future. His best-known rhythm guitar pattern (three strokes/rest/two strokes, or “shave and a haircut, two bits”) influenced many. The “Bo Diddley beat,” as it came to be known, appeared on records by Buddy Holly, the Rolling Stones, Bruce Springsteen, U2, rapper B.o.B., and many others. In Bo Diddley’s own songs, the “Bo Diddley beat” was often combined with remarkably simple chord changes, as can be heard on his self-titled debut single, “Bo Diddley.” Throughout that single-chord song, which went to No. -
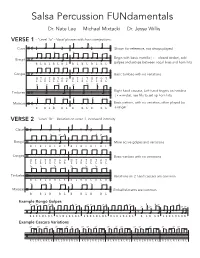
Salsa Percussion Fundamentals Dr
Salsa Percussion FUNdamentals Dr. Nate Lee Michael Mixtacki Dr. Jesse Willis VERSE 1 - "Level 1a" - Vocal phrases with horn interjections j Clave C Œ œ œ Œ œ ‰ œ Œ œ Shown for reference, not always played ã + + + + Begin with basic martillo (+ = closed stroke), add Bongó œ 1 œ 1 œ 1 œ 1 œ 1 œ 1 œ 1 œ 1 ã C R L R L R L R L R L R L R L R L golpes and setups between vocal lines and horn hits Congas œ œ x œ œ œ œ œ œ œ x œ œ œ œ œ Basic tumbao with no variations ã C H T S T H T O O H T S T H T O T L L R L L L R R L L R L L L R L > > > > > > x x x x x x x x xj x Right hand cascara, Left hand fingers on hembra Timbales Å e Å e ã C ‰ ( x = mute), use fills to set up horn hits - . - . - . - . Maracas œ œ œ œ œ œ œ œ œ œ œ œ Basic pattern, with no variation, often played by ã C R R L R R L R R L R R L a singer VERSE 2 - "Level 1b" - Variation on verse 1, increased intensity Clave œ œ œ œj œ ã Œ Œ ‰ Œ + + ^ ^ œ 1 œ 1 œ 1 > x œ 1 œ 1 œ x > 1 Bongó œ œ More active golpes and variations ã R L R L R L R L R L R L R L R L Congas œ œ x œ œ œ œ œ œ œ x œ œ œ œ œ Basic tumbao with no variations ã H T S T H T O O H T S T H T O T L L R L L L R R L L R L L L R L > > > > > > x x x x x x x x x x x x x x x x Timbales Variations on 2-hand cascara are common ã R L R L R R L R R L R R L R L R - . -

“Bo Diddley” and “I'm a Man” (1955)
“Bo Diddley” and “I’m a Man” (1955) Added to the National Registry: 2011 Essay by Ed Komara (guest post)* Bo Diddley While waiting in Bo Diddley’s house to conduct an interview for the February 12, 1987 issue of “Rolling Stone,” journalist Kurt Loder noticed a poster. “If You Think Rock and Roll Started With Elvis,” it proclaimed, “You Don’t Know Diddley.” This statement seems exaggerated, but upon listening to Diddley’s April 1955 debut 78 on Checker 814, “Bo Diddley” backed with “I’m A Man,” it becomes apt, perhaps even understated. Bo Diddley (1928-2008) described his own place in music history to Loder. “People wouldn’t even bother with no stuff like ‘Bo Diddley’ and ‘I’m A Man’ and stuff like that ten years earlier [circa 1945] or even a year earlier [1954]. Then Leonard and Phil Chess decided to take a chance, and suddenly a whole different scene, a different kind of music, came in. And that was the beginning of rock and roll.” The composer credit for Checker 814 reads “E. McDaniels,” and there begins the tale. Bo Diddley was born Ellas Otha Bates in McComb, Mississippi on December 30, 1928 to a teenage mother and her local boyfriend. He was raised, however, by his maternal first cousin, Gussie McDaniel, to whom he was taken to Chicago, and given her surname McDaniel. He grew up on the South Side of the city, where he learned violin, trombone and, at age 12, the guitar. Before long, he was playing for change on the local streets. -

Cuban Music Teaching Unit
Thesis Advisor: Frank Martignetti THE MUSIC AND DANCE OF CUBA: by Melissa Salguero Music Education Program Submitted in partial fulfillment of the requirements for the degree Master of Science in Elementary Education in the School of Education University of Bridgeport 2015 © 2015 by Melissa Salguero Salguero 2 Abstract (Table of Contents) This unit is designed for 5th grade students. There are 7 lessons in this unit. Concept areas of rhythm, melody, form, and timbre are used throughout the unit. Skills developed over the 7 lessons are singing, moving, listening, playing instruments, reading/writing music notation, and creating original music. Lesson plans are intended for class periods of approximately 45-50 minutes. Teachers will need to adapt the lessons to fit their school’s resources and the particular needs of their students. This unit focuses on two distinct genres of Cuban music: Son and Danzón. Through a variety of activities students will learn the distinct sound, form, dance, rhythms and instrumentation that help define these two genres. Students will also learn about how historical events have shaped Cuban music. Salguero 3 Table of Contents: Abstract……………………………………………..…………………………..2 Introduction……………………………………….……………………………4 Research…………………………………………..……………………………5 The Cuban Musical Heritage……………….……………………………5 The Discovery of Cuba…….……………………………………………..5 Indigenous Music…...…………………………………………………….6 European Influences……………………………………………….……..6 African Influences………………………………………………………...7 Historical Influences……………………….……………………………..7 -

Blues CD Reviews
In This Issue... April Blues Bash: Son Jack, Jr. KBA Photographer Suzanne Swanson Dawn Tyler Watson (IBC First Place Band) (Photo by Daniel Sheehan) (Photo by Paul Brown) (Photo by Paul Brown) Letter from the President 2 Remembering James Cotton 6 Membership Opportunities 14 Letter from the Editor 3 April Blues Bash Preview 11 B Sharp Coffee House 15 Officers and Directors 4 Memphis Memo 12 Extended CD Review 16 On the Cover 4 New Venue: Cask & Trotter 14 Hawkeye Herman in Spokane! 17 Letter from Washington Blues Society President Tony Frederickson Kevin Sutton & the Blue Monday Band opening American Indian Chief and several bidders really Hi Blues Fans, the show and getting the crowd in a fevered pitch went to work on this item and provided as much that never let up the whole evening. We had many excitement as the music we had already heard. The This past month the Washington Blues Society, special guests throughout the show and the Blue silent auction closed and almost every item had Lee Oskar Harmonicas, and Anacortes Brewery Monday Band invited Jimmy Fadden to sit in multiple bids and displayed the generosity of those (H2O & Rockfish) sponsored the first of what we with them which raised the bar even higher. After in attendance. Our last special guest of the evening hope will be an annual fundraising event for the a brief break for a set change and live auction, was Mark Dufresne who led the Lee Oskar band Washington Blues Society’s Musician Relief Fund Bobby Holland & the Breadline took the stage with a few songs in memory of James Cotton, who at the Historic Everett Theater. -

Learning Activities: Song #11 ~~ Don't-Be-Moody-Do-Yo
LEARNING ACTIVITIES: ©GayeAdegbalola SONG #11 ~~ DON'T-BE-MOODY-DO-YO'-DUTY SONG FLAVOR: BO DIDDLEY BEAT • Maracas are musical instruments that sound likearattle. Many Bo Diddleysongs featurethesoundof maracas. (Don't know Bo? See below.) You can makeyour own maracas from recycled materials. Take 2 plastic water bottles. Make sure they are dry. Fill about 1/4 full of dried beans. Seal the lidswith tape. Getto shakin'! • This song is full ofopposites: open&close, down & up,on&off,right&wrong, borrow & return. Can you thinkofother opposites? Try to come up withatleast 10. Now try to makethem "action" wordslikedropping down &picking up or opening and closing. • When we try to think of ideas, an easy waytodo so is by brainstorming. Itis a way to solve problems bycomingup withas many ideas as possible. Youare encouraged to come up withnew, creative ideas without judgingwhether they are goodor bad, realistic or not. For example, think of 10 uses for anempty plastic bottle. Of course,weknow it can be used for holdingliquids, butitcan also be cut so that it can be used as a shovel, or for making maracas, or as a noise maker. Thelonger we think,usually the more interesting our ideas become. Here'sagood brainstorming exercise: Comeup with50uses forapaper clip. •Inthis song,we are singing about how to respondto a problem. Sometimespeople behave inunacceptable ways. For example, sometimes it is hard to ask people topick up somethingthey've droppedonthe ground. Many newspapers have an advice column. In this column,people write in toask advice about how to handle certain situations. Someofthese are about personal relations.