Non-Periodic Homogenization for Elastic Wave Propagation in Complex Media
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Page 1 of 29 Applist.Me — There's a List for That! 7/20/2012
applist.me — There's a list for that! Page 1 of 29 469 Apps 101 Science 3D Sun 4th Grade Math: Splash Centered Systems Dr. Tony Phillips, L Math Wo v.1.1 –0.5MB v.3.5 –6MB StudyPad, Inc. v.2.2.1 – 22MB THIS VERSION WILL WORK WITH OS 3.0 OR A major solar flare erupts on the sun. Splash Math is a fun and innovative way ABOVE ONLY. A BACKWARD COMPATIBLE Before long, your phone chirps in your to practice math. With 12 chapters UPDATE WILL BE RELEASED SHOR... pocket to let you know... covering over 140+ math w... View in the App Store. View in the App Store. View in the App Store. 8 Planets A Bee Sees - Learning A Bee Sees Puzzles - BrightSlide LLC Letters, Learn Sha v.2.0 –11MB Headlight Software, Headlight Software, v.1.5 –8.7MB v.1.1 –13.4MB Download the the critically acclaimed The happy, balloon popping bee helps The happy bee helps kids learn letters, educational application 8 Planets. 8 kids learn Letters, Numbers, and Colors. numbers, and shapes with fun puzzles Planets features four gam... With easy to use contr... you can customize yours... View in the App Store. View in the App Store. View in the App Store. A Phonics introduction A Sight Words Read and ABA Flash Cards & app - H Spell a Games - Emot Hetal Shah Hetal Shah Innovative Mobile Ap v.1.0 –18.6MB v.1.0 –9MB v.4.2 –26.3MB If you the parent are familiar with phonics Features: 1) 300 sight words from Dolch ★★★★★ A fun, simple, and easy way to you will immediately appreciate the way list 2) Presented by grade level 3) Two learn to recognize emotions. -

March 2019 LOCAL HERO: WHY LOCAL MEDIA MATTERS
March 2019 LOCAL HERO: WHY LOCAL MEDIA MATTERS After a month of buyouts and announcements, the dial’s interest news. Culture Secretary Jeremy Wright responded been moved on local radio. Global Radio recently announced with a rallying cry to the industry, claiming it can “overcome it would no longer air regional breakfast and drivetime shows the challenges it faces from a changing market”. in favour of national programming, while NewsUK has sold off most of its local radio stations to invest in its national stations Local media isn’t just of benefit to the public interest but can talkSPORT and Virgin Radio. be to advertisers as well. The move from Global, described as “a huge step for the A huge amount of Brits still have a strong sense of local commercial radio sector”, will see 40 of its local breakfast identity, with 90% agreeing they are proud of the area they shows replaced by national programming across the Capital, live in (“Consumer Catalyst”). Local media allows consumers Smooth and Heart networks. Drivetime, evening and to feel a part of their community – even if it’s as simple as weekend programmes will also be reduced, and ten of its 24 hearing local voices and regional accents on the radio, as local stations – including Cambridge, Norwich, Essex and Kent argued by broadcaster Mark Lawson. – will be closed. The announcement comes as part of Global’s longer-term project to bring hundreds of local stations into Brands can tap into this, ensuring they speak to consumers in several national brands – and puts over 100 jobs at risk. -

About Endgame
IN ASSOCIATION WITH BLINDER FILMS presents in coproduction with UMEDIA in association with FÍS ÉIREANN / SCREEN IRELAND, INEVITABLE PICTURES and EPIC PICTURES GROUP THE HAUNTINGS BEGIN IN THEATERS MARCH, 2020 Written and Directed by MIKE AHERN & ENDA LOUGHMAN Starring Maeve Higgins, Barry Ward, Risteárd Cooper, Jamie Beamish, Terri Chandler With Will Forte And Claudia O’Doherty 93 min. – Ireland / Belgium – MPAA Rating: R WEBSITE: www.CrankedUpFilms.com/ExtraOrdinary / http://rosesdrivingschool.com/ SOCIAL MEDIA: Facebook - Twitter - Instagram HASHTAG: #ExtraOrdinary #ChristianWinterComeback #CosmicWoman #EverydayHauntings STILLS/NOTES: Link TRAILER: https://www.youtube.com/watch?v=x1TvL5ZL6Sc For additional information please contact: New York: Leigh Wolfson: [email protected]: 212.373.6149 Nina Baron: [email protected] – 212.272.6150 Los Angeles: Margaret Gordon: [email protected] – 310.854.4726 Emily Maroon – [email protected] – 310.854.3289 Field: Sara Blue - [email protected] - 303-955-8854 1 LOGLINE Rose, a mostly sweet & mostly lonely Irish small-town driving instructor, must use her supernatural talents to save the daughter of Martin (also mostly sweet & lonely) from a washed-up rock star who is using her in a Satanic pact to reignite his fame. SHORT SYNOPSIS Rose, a sweet, lonely driving instructor in rural Ireland, is gifted with supernatural abilities. Rose has a love/hate relationship with her ‘talents’ & tries to ignore the constant spirit related requests from locals - to exorcise possessed rubbish bins or haunted gravel. But! Christian Winter, a washed up, one-hit-wonder rock star, has made a pact with the devil for a return to greatness! He puts a spell on a local teenager- making her levitate. -

Publishing During a Pandemic
Publishing during a pandemic Gearing up for a hybrid future as we move into a post-Covid world AUGUST 2020 UPDATE Contents 01 Clocking in: a hybrid workplace / p04 02 Innovation: the only way out / p10 03 Content: words with purpose / p17 04 Networking: a virtual reality / p22 05 Revenue: evolution to revolution / p27 Writers: Piet van Niekerk; Pierre de Villiers Editor: Sylkia J. Cartagena Designer: Ian Crawford © FIPP. All rights reserved 02 Introduction Looking beyond Covid-19 IPP’s first two ‘Publishing during a - publishers are starting to understand what informed predictions - including what pandemic’ Covid-19 reports mapped the long-term impact of Covid-19 on their the new workplace may look like and Fpublishers’ initial response to the industry might be. While this third report - how we will now approach networking. coronavirus pandemic. The first analysed the ‘Publishing during a pandemic: Gearing up immediate impact of realities such as the for a hybrid future’ - continues to shed light By keeping track of the impact, response and, loss of newsstands, a slump in ad spending on early lessons learnt, it’s main focus is on ultimately, our industry’s survival strategies, and limitations on content creation. The how publishing might look in the future. FIPP is not only recording the process of second report then looked at how the industry dealing with this crisis but also mapping a way was standing up to the early challenges. Some chapters continue to make for grim to overcome future challenges. FIPP’s belief reading (we cannot ignore the dismal remains that by sharing thoughts, experiences With the benefit of hindsight - and with many facts), but there are also pleasant surprises and learnings during such a time enables the knee-jerk responses having now played out and many examples of innovation and entire industry to learn, and survive, together. -

Aibs-Shortlist-2-2020.Pdf
The AIBs 2020 The Shortlist TV and VIDEO Arts and culture The Dancer Thieves Banyak Films for Witness, Al Jazeera English The Red Door Project: Evolve Blue Chalk Media for The Red Door Project Spirit of Tokyo CNN Beethoven’s Ninth: Symphony for the World Deutsche Welle Matera Traveller Iran International Miyako, The Last Dance NHK in association with NHK Enterprises Chinese Folk Opera Phoenix Satellite Television Human interest MENtal Health: Breaking the Silence 5 News, ITN Fly on the Wall: The Virus Al Jazeera English Online Word of Truth: Transgender Arabs Living in the Middle East Alhurra Television African Voices: Female Pilots CNN Surviving the Special Forces De Mensen PANO: Secret on Instagram één for VRT Off the Grid: Missing Babies TRT World The Skin we Wear Very! For CNA, Mediacorp Pte Ltd Supporters of the AIBs 2020 The AIBs 2020 The Shortlist Natural world Fault Lines - Amazon Burning: Death and Destruction in Brazil’s Rainforest Al Jazeera English Borneo is Burning CNN Chris Packham: Plant A Tree to Save the World ITN Productions Sinking Island Radio Free Asia Freed to be Wild RT VOA Films: Illegal Logging Inside Mexico Monarch Butterfly Sanctuary VOA (Voice of America) Australia's Ocean Odyssey: A Journey Down the Wild Pacific Media for Australian Broadcasting East Australian Current Corporation and ARTE France Science and technology The Big Picture: The World According to A.I. Al Jazeera English Refugee Gardens: Turning Old Mattresses into Fresh Food BBC News Inventing Tomorrow CNN WFH: New Reality CNN Coded World Peddling -

Sanoma Vuosikatsaus 2019
Vuosikatsaus 2019 Sisällys Vuosi 2019 lyhyesti Selvitys hallinto- ja ohjausjärjestelmästä 113 Vuosi 2019 lukuina 2 Sanoman transformaatio 3 Palkka- ja palkkioselvitys 125 Yritysostot ja -myynnit 2019 4 Sanoma sijoituskohteena 5 Sijoittajille 129 Sanoman arvonluontimalli 7 Yritysvastuu Sanomalla 8 Hallituksen puheenjohtajan tervehdys 9 Toimitusjohtajan tervehdys 11 Hallituksen toimintakertomus 14 Tilinpäätös Konsernin tuloslaskelma 34 Konsernin laaja tuloslaskelma 35 Sanoman vuosikatsaus 2019 sisältää seuraavat osat: Konsernitase 36 1. Hallituksen toimintakertomus mukaan lukien muut kuin taloudelliset tiedot Laskelma oman pääoman muutoksista 37 2. Konsernin ja emoyhtiön tilintarkastettu tilinpäätös 3. Selvitys hallinto- ja ohjausjärjestelmästä Konsernin rahavirtalaskelma 38 4. Palkka- ja palkkioselvitys Konsernitilinpäätöksen liitetiedot 40 Ellei toisin ilmoiteta, kaikki esitetyt tuloslaskelmaan liittyvät luvut vuosilta 2018 ja 2019 sisältävät vain jatkuvat toiminnot. Taseeseen ja rahavirtaan Emoyhtiön tilinpäätös 96 liittyvät luvut sisältävät sekä jatkuvat että lopetetut toiminnot. Lisätietoja Sanomasta sijoituskohteena on saatavilla osoitteessa Hallituksen voitonjakoehdotus 106 sanoma.com/fi/sijoittajat Tilintarkastuskertomus 107 Tilintarkastettu Osa hallituksen toimintakertomusta Vuosi 2019 Hallituksen toimintakertomus Tilinpäätös Selvitys hallinto- ja ohjausjärjestelmästä Palkka- ja palkkioselvitys Vuosi 2019 lukuina Operatiivinen liikevoittoprosentti ilman hankintamenojen poistoja Learningin tulos parani, Media Finlandin tulos pysyi -

The Distribution Channel Survey in Uk Market for Sports Travel Theme (2020)
THE DISTRIBUTION CHANNEL SURVEY IN UK MARKET FOR SPORTS TRAVEL THEME (2020) Marjo Ranta-Irwin Blueberry Consulting September 2020 2 SPORT TOURISM IS MOVING PEOPLE Sport business is one of the most growing industries globally and its importance to national economies is significant. This includes multiple sectors and sport is often combined with recreation or wellness or other close industry areas. Defining what is included in sport as an industry area is therefore challenging. Sport tourism is an essential part of this development and sports, and especially, sporting events move tourists around the world. Various sports and outdoor events that take place in Finland gather both international participants and spectators; the regional economic impact of sport events is great. Visit Finland has been developing, promoting and marketing sports travel since 2017. The focus being on leisure travel for the international travellers interested in adventure, sports and active wellness holidays. The goal of this distribution channel survey was to define and find those sports tourism distribution channels and media contacts which are relevant to the UK market. The channels for this report were chosen from a wide range of different channels by evaluating the importance, relevancy or potential from the Finnish tourism and sports industry point of view. In addition to the online specialist tour operators, this survey also lists some media and marketing sites, influencers, communities, sports clubs and sport federations. The sports activities which were included in this survey were • running (marathon, trail running or similar) • hiking / walking • cycling (road, MTB, touring, events, year-round) • golf • motor sports This channel survey was produced for Business Finland by Blueberry Consulting in 2020. -

Immediate Media Co and Black Dog Media Join Cafeyn's Information
Immediate Media Co and Black Dog Media join Cafeyn’s information streaming platform Submitted by: Martha Thierion de Monclin T/A Bijou PR Friday, 20 March 2020 London, 19th March, 2020 -- Cafeyn (https://www.cafeyn.co/uk/newsstand/), the popular European information streaming service, announces the signature of Immediate Media Co (http://www.immediate.co.uk/) and Black Dog Media (https://bdmpublications.com/) to the Cafeyn platform. More than sixty new titles, including Immediate’s BBC magazine titles and Black Dog Media’s tech guides, are now live and available to subscribers of the Cafeyn information streaming platform. With an already extensive catalogue, Cafeyn aims to offer the largest and most diverse portfolio that allows customers to freely explore and discover different themes and topics. Immediate Media is the special interest content and platform company. Its fast-growing, multi-platform media business owns and operates some of the best-loved brands in the UK, including Olive, Homes and Antiques and Cycling Plus. Immediate Media publishes a wide range of titles under licence from the BBC as BBC Good Food, BBC Countryfile magazine, BBC Top Gear, Lonely Planet and BBC Gardeners’ World magazine. From its humble beginnings in 2004, Black Dog Media quickly grew from a single publication produced by a team of just two, to one of the biggest names in global bookazine publishing. The company has a portfolio of over 250 publications, delivered by its international staff with titles ranging from the Complete Guide to Photography to the Complete Guide to MacOS. The partnership with Black Dog Media brings its guidebooks and tech guides to the platform, allowing users to improve their skills in a broad range of technical fields. -
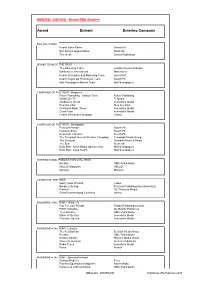
Nma2020 – Shortlist.2
NMA2020 JUDGING - Round ONE Shortlist Award Entrant Entering Company Best Use of Data Hearst Value Packs Hearst UK Sun Savers segmentation News UK The Week Dennis Publishing BRAND TEAM OF THE YEAR The Marketing Team London Review of Books Marketforce International Marketforce Hearst Circulation and Marketing Team Hearst UK Reach Regionals Promotions Team Reach Plc Mail Newspapers Market Team Mail Newspapers CAMPAIGN OF THE YEAR - Magazine Future Publishing - Various Titles Future Publishing What's On TV TI Media Gardeners' World Immediate Media New Scientist New Scientist Christmas Radio Times Immediate Media Good Food Immediate Media Hearst Christmas Campaign Hearst CAMPAIGN OF THE YEAR - Newspaper Plymouth Herald Reach Plc Liverpool Echo Reach Plc Newcastle Chronicle Reach Plc The Telegraph General Election Campaign Telegraph Media Group The Guardian Guardian News & Media The Sun News UK Daily Mail - Great British Spring Clean Mail Newspapers Daily Mail - Good Health Mail Newspapers INTERNATIONAL PUBLICATION of the YEAR Breathe GMC Publications HELLO! Magazine HELLO! Monocle Monocle LAUNCH OF THE YEAR Match Attax 2019/20 Topps Simply Lettering Practical Publishing International Ltd Platinum DC Thomson Media Good Housekeeping Collection Hearst MAGAZINE of the YEAR - Children's Fun To Learn Friends Redan Publishing Limited PONY Magazine DJ Murphy Publishers Teen Breathe GMC Publications Match of the Day Immediate Media Cbeebies Special Immediate Media MAGAZINE of the YEAR - Lifestyle The Red Bulletin Red Bull Media House Breathe GMC Publications -

Professional Publishers Association—Written Evidence (FOJ0046)
Professional Publishers Association—written evidence (FOJ0046) House of Lords Select Committee on Communications and Digital Call for Evidence – The Future of Journalism About Us The Professional Publishers Association (PPA) is the membership network for UK consumer magazine media and business information publishers, representing around 200 of the UK’s most renowned publishing houses. With more than 40 million adults in the UK reading magazine media every month, the sector is worth £4 billion to the UK economy, employing more than 100,000 people. The PPA's membership incorporates the UK’s largest publishing houses, including Bauer Media Group, Centaur, Condé Nast, Dennis Publishing, The Economist, Haymarket Media Group, Hearst UK, Immediate Media, TI Media, and William Reed Business Media as well as many smaller independent publishers. A full list of members can be found here: www.ppa.co.uk/Resources/Members Executive Summary PPA welcomes the opportunity to submit evidence to the Select Committee on Communications and Digital, following its decision to investigate the future of journalism in the UK. This is a timely and important piece of work, given the current circumstances and economic impact the coronavirus (COVID-19) pandemic is having on the publishing industry. PPA members play a valuable role within society and the economy, not least in these times to keep the public informed, educated and importantly entertained; as well as providing essential business information in the B2B sector to keep the economic wheels greased and turning. It is therefore vital that the industry survives this crisis and emerges on the other side as strong, viable businesses. -

Exhibitor Pack 2020
EXHIBITOR PACK 2020 the SCOTTISH QUILTING show GETTING THE NATION CRAFTING The CREATIVE Craft Show, alongside its sister shows attract over 154,000 visitors annually. Our 9 Creative Craft Shows, held at premier UK exhibition venues, attract the UK’s largest collections of creative supplies available under one roof. Home to some of the biggest names in the craft industry, we have exhibitors attending from across the globe offering shopping, displays, demonstrations, workshops and interactive sessions. WHO ARE ICHF EVENTS? We’re the UK’s leading organiser of lifestyle and hobby events. From the company’s formation in 1976, we now manage over 20 hugely successful consumer shows annually. “We have worked with ICHF for a number of years and exhibit at many of their shows. We find the team helpful and professional to deal with. As well as selling our products we run make & takes on our stand which are always popular. The shows are well attended with the right type of customers.” - Maggie, The Arty Crafty Place OUR VISITORS PROFILE • Female Over 154,000 annual visitors • Retired • Empty Nesters 7% Growth year on year • Affluent 75% Female attendess • Mail order shoppers • Internet Users 40 - 60 Years - average age of attendess • Home owners • Disposable income 70% ABC1 social demographic • Community spirited OUR REACH Direct contact with over 500,000 craft and hobby fans across our digital platforms. We reach 7.5 million TI Media UK crafters through various magazine titles. Follow us at @thecraftshows #thecraftshows WHERE ARE WE IN 2020? EVENTCITY, MANCHESTER NEC, BIRMINGHAM Featuring 30 Jan - 1 Feb 10,000 visitors 19 - 22 March 28,000 visitors 3 - 5 September 10,000 visitors 26 - 28 June 10,000 visitors As the second largest exhibition space in the UK 5 - 8 November 45,000 visitors outside of London, EventCity is a contemporary venue Adjacent to Birmingham Airport and Birmingham located next to The Trafford Centre. -

Future Shares in Jurisdictions Other Than the United Kingdom, May Be Restricted by Law
THIS DOCUMENT IS IMPORTANT AND REQUIRES YOUR IMMEDIATE ATTENTION. If you are in any doubt about the contents of this document or the action you should take, you are recommended to seek your own financial or professional advice immediately from your stockbroker, bank, solicitor, accountant, fund manager or other appropriate independent financial adviser duly authorised under the Financial Services and Markets Act 2000 (as amended) if you are resident in the United Kingdom or, if not, from another appropriately authorised independent financial or professional adviser. If you sell or have sold or otherwise transferred all of your Ordinary Shares, please send this document, together with the accompanying form of proxy, as soon as possible to the purchaser or transferee, or to the stockbroker, bank or other agent through whom the sale or transfer was effected, for onward transmission to the purchaser or transferee. If you sell or have sold or otherwise transferred only part of your holding of Ordinary Shares, you should retain this document and the accompanying form of proxy and you should consult with the stockbroker, bank or other agent through whom the sale or transfer was effected. Any person (including, without limitation, custodians, nominees, and trustees) who may have a contractual or legal obligation or may otherwise intend to forward this document and any accompanying documents to any jurisdiction outside the United Kingdom should seek appropriate advice before taking any such action. The release, publication or distribution of this document and any accompanying documents into or from jurisdictions other than the United Kingdom, and the allotment of New Future Shares in jurisdictions other than the United Kingdom, may be restricted by law.