Measurements & Uncertainties
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dial Caliperscalipers at the Conclusion of This Presentation, You Will Be Able To…
Forging new generations of engineers DialDial CalipersCalipers At the conclusion of this presentation, you will be able to… identify four types of measurements that dial calipers can perform. identify the different parts of a dial caliper. accurately read an inch dial caliper. DialDial CalipersCalipers GeneralGeneral InformationInformation DialDial CalipersCalipers are arguably the most common and versatile of all the precision measuring tools. Engineers, technicians, scientists and machinists use precision measurement tools every day for: • analysis • reverse engineering • inspection • manufacturing • engineering design DialDial CalipersCalipers FourFour TypesTypes ofof MeasurementsMeasurements Dial calipers are used to perform four common measurements on parts… 1. Outside Diameter/Object Thickness 2. Inside Diameter/Space Width 3. Step Distance 4. Hole Depth OutsideOutside MeasuringMeasuring FacesFaces These are the faces between which outside length or diameter is measured. InsideInside MeasuringMeasuring FacesFaces These are the faces between which inside diameter or space width (i.e., slot width) is measured. StepStep MeasuringMeasuring FacesFaces These are the faces between which stepped parallel surface distance can be measured. DepthDepth MeasuringMeasuring FacesFaces These are the faces between which the depth of a hole can be measured. Note: Work piece is shown in section. Dial Caliper shortened for graphic purposes. DialDial CalipersCalipers NomenclatureNomenclature A standard inchinch dialdial calipercaliper will measure slightly more than 6 inches. The bladeblade scalescale shows each inch divided into 10 increments. Each increment equals one hundred thousandths (0.100”). Note: Some dial calipers have blade scales that are located above or below the rack. BladeBlade The bladeblade is the immovable portion of the dial caliper. SliderSlider The sliderslider moves along the blade and is used to adjust the distance between the measuring surfaces. -

Check Points for Measuring Instruments
Catalog No. E12024 Check Points for Measuring Instruments Introduction Measurement… the word can mean many things. In the case of length measurement there are many kinds of measuring instrument and corresponding measuring methods. For efficient and accurate measurement, the proper usage of measuring tools and instruments is vital. Additionally, to ensure the long working life of those instruments, care in use and regular maintenance is important. We have put together this booklet to help anyone get the best use from a Mitutoyo measuring instrument for many years, and sincerely hope it will help you. CONVENTIONS USED IN THIS BOOKLET The following symbols are used in this booklet to help the user obtain reliable measurement data through correct instrument operation. correct incorrect CONTENTS Products Used for Maintenance of Measuring Instruments 1 Micrometers Digimatic Outside Micrometers (Coolant Proof Micrometers) 2 Outside Micrometers 3 Holtest Digimatic Holtest (Three-point Bore Micrometers) 4 Holtest (Two-point/Three-point Bore Micrometers) 5 Bore Gages Bore Gages 6 Bore Gages (Small Holes) 7 Calipers ABSOLUTE Coolant Proof Calipers 8 ABSOLUTE Digimatic Calipers 9 Dial Calipers 10 Vernier Calipers 11 ABSOLUTE Inside Calipers 12 Offset Centerline Calipers 13 Height Gages Digimatic Height Gages 14 ABSOLUTE Digimatic Height Gages 15 Vernier Height Gages 16 Dial Height Gages 17 Indicators Digimatic Indicators 18 Dial Indicators 19 Dial Test Indicators (Lever-operated Dial Indicators) 20 Thickness Gages 21 Gauge Blocks Rectangular Gauge Blocks 22 Products Used for Maintenance of Measuring Instruments Mitutoyo products Micrometer oil Maintenance kit for gauge blocks Lubrication and rust-prevention oil Maintenance kit for gauge Order No.207000 blocks includes all the necessary maintenance tools for removing burrs and contamination, and for applying anti-corrosion treatment after use, etc. -
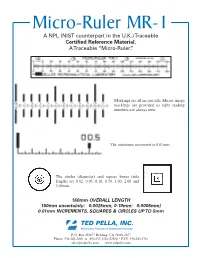
Micro-Ruler MR-1 a NPL (NIST Counterpart in the U.K.)Traceable Certified Reference Material
Micro-Ruler MR-1 A NPL (NIST counterpart in the U.K.)Traceable Certified Reference Material . ATraceable “Micro-Ruler”. Markings are all on one side. Mirror image markings are provided so right reading numbers are always seen. The minimum increment is 0.01mm. The circles (diameter) and square boxes (side length) are 0.02, 0.05, 0.10, 0.50, 1.00, 2.00 and 5.00mm. 150mm OVERALL LENGTH 150mm uncertainty: ±0.0025mm, 0-10mm: ±0.0005mm) 0.01mm INCREMENTS, SQUARES & CIRCLES UP TO 5mm TED PELLA, INC. Microscopy Products for Science and Industry P. O. Box 492477 Redding, CA 96049-2477 Phone: 530-243-2200 or 800-237-3526 (USA) • FAX: 530-243-3761 [email protected] www.tedpella.com DOES THE WORLD NEED A TRACEABLE RULER? The MR-1 is labeled in mm. Its overall scale extends According to ISO, traceable measurements shall be over 150mm with 0.01mm increments. The ruler is designed to be viewed from either side as the markings made when products require the dimensions to be are both right reading and mirror images. This allows known to a specified uncertainty. These measurements the ruler marking to be placed in direct contact with the shall be made with a traceable ruler or micrometer. For sample, avoiding parallax errors. Independent of the magnification to be traceable the image and object size ruler orientation, the scale can be read correctly. There is must be measured with calibration standards that have a common scale with the finest (0.01mm) markings to traceable dimensions. read. We measure and certify pitch (the distance between repeating parallel lines using center-to-center or edge-to- edge spacing. -

Verification Regulation of Steel Ruler
ITTC – Recommended 7.6-02-04 Procedures and guidelines Page 1 of 15 Effective Date Revision Calibration of Micrometers 2002 00 ITTC Quality System Manual Sample Work Instructions Work Instructions Calibration of Micrometers 7.6 Control of Inspection, Measuring and Test Equipment 7.6-02 Sample Work Instructions 7.6-02-04 Calibration of Micrometers Updated / Edited by Approved Quality Systems Group of the 28th ITTC 23rd ITTC 2002 Date: 07/2017 Date: 09/2002 ITTC – Recommended 7.6-02-04 Procedures and guidelines Page 2 of 15 Effective Date Revision Calibration of Micrometers 2002 00 Table of Contents 1. PURPOSE .............................................. 4 4.6 MEASURING FORCE ......................... 9 4.6.1 Requirements: ............................... 9 2. INTRODUCTION ................................. 4 4.6.2 Calibration Method: ..................... 9 3. SUBJECT AND CONDITION OF 4.7 WIDTH AND WIDTH DIFFERENCE CALIBRATION .................................... 4 OF LINES .............................................. 9 3.1 SUBJECT AND MAIN TOOLS OF 4.7.1 Requirements ................................ 9 CALIBRATION .................................... 4 4.7.2 Calibration Method ...................... 9 3.2 CALIBRATION CONDITIONS .......... 5 4.8 RELATIVE POSITION OF INDICATOR NEEDLE AND DIAL.. 10 4. TECHNICAL REQUIREMENTS AND CALIBRATION METHOD ................. 7 4.8.1 Requirements .............................. 10 4.8.2 Calibration Method: ................... 10 4.1 EXTERIOR ............................................ 7 4.9 DISTANCE -

Vernier Caliper and Micrometer Computer Models Using Easy Java Simulation and Its Pedagogical Design Features—Ideas for Augmenting Learning with Real Instruments
Wee, Loo Kang, & Ning, Hwee Tiang. (2014). Vernier caliper and micrometer computer models using Easy Java Simulation and its pedagogical design features—ideas for augmenting learning with real instruments. Physics Education, 49(5), 493. Vernier caliper and micrometer computer models using Easy Java Simulation and its pedagogical design feature-ideas to augment learning with real instruments Loo Kang WEE1, Hwee Tiang NING2 1Ministry of Education, Educational Technology Division, Singapore 2 Ministry of Education, National Junior College, Singapore [email protected], [email protected] Abstract: This article presents the customization of EJS models, used together with actual laboratory instruments, to create an active experiential learning of measurements. The laboratory instruments are the vernier caliper and the micrometer. Three computer model design ideas that complement real equipment are discussed in this article. They are 1) the simple view and associated learning to pen and paper question and the real world, 2) hints, answers, different options of scales and inclusion of zero error and 3) assessment for learning feedback. The initial positive feedback from Singaporean students and educators points to the possibility of these tools being successfully shared and implemented in learning communities, and validated. Educators are encouraged to change the source codes of these computer models to suit their own purposes, licensed creative commons attribution for the benefit of all humankind. Video abstract: http://youtu.be/jHoA5M-_1R4 2015 Resources: http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/5-vernier-caliper http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/6-micrometer Keyword: easy java simulation, active learning, education, teacher professional development, e–learning, applet, design, open source physics PACS: 06.30.Gv 06.30.Bp 1.50.H- 01.50.Lc 07.05.Tp I. -

Vernier Scale 05/31/2007 04:10 PM
Vernier Scale 05/31/2007 04:10 PM 1. THE VERNIER SCALE Equipment List: two 3 X 5 cards one ruler incremented in millimeters What you will learn: This lab teaches how a vernier scale works and how to use it. I. Introduction: A vernier scale (Pierre Vernier, ca. 1600) can be used on any measuring device with a graduated scale. Most often a vernier scale is found on length measuring devices such as vernier calipers or micrometers. A vernier instrument increases the measuring precision beyond what it would normally be with an ordinary measuring scale like a ruler or meter stick. II. How a vernier system works: A vernier scale slides across a fixed main scale. The vernier scale shown below in figure 1 is subdivided so that ten of its divisions correspond to nine divisions on the main scale. When ten vernier divisions are compressed into the space of nine main scale divisions we say the vernier-scale ratio is 10:9. So the divisions on the vernier scale are not of a standard length (i.e., inches or centimeters), but the divisions on the main scale are always some standard length like millimeters or decimal inches. A vernier scale enables an unambiguous interpolation between the smallest divisions on the main scale. Since the vernier scale pictured above is constructed to have ten divisions in the space of nine on the main scale, any single division on the vernier scale is 0.1 divisions less than a division on the main scale. http://nebula.deanza.fhda.edu/physics/Newton/4A/4ALabs/Vernier_Scale.html Page 1 of 5 Vernier Scale 05/31/2007 04:10 PM scale, any single division on the vernier scale is 0.1 divisions less than a division on the main scale. -

MICHIGAN STATE COLLEGE Paul W
A STUDY OF RECENT DEVELOPMENTS AND INVENTIONS IN ENGINEERING INSTRUMENTS Thai: for III. Dean. of I. S. MICHIGAN STATE COLLEGE Paul W. Hoynigor I948 This]: _ C./ SUPP! '3' Nagy NIH: LJWIHL WA KOF BOOK A STUDY OF RECENT DEVELOPMENTS AND INVENTIONS IN ENGINEERING’INSIRUMENTS A Thesis Submitted to The Faculty of MICHIGAN‘STATE COLLEGE OF AGRICULTURE AND.APPLIED SCIENCE by Paul W. Heyniger Candidate for the Degree of Batchelor of Science June 1948 \. HE-UI: PREFACE This Thesis is submitted to the faculty of Michigan State College as one of the requirements for a B. S. De- gree in Civil Engineering.' At this time,I Iish to express my appreciation to c. M. Cade, Professor of Civil Engineering at Michigan State Collegeafor his assistance throughout the course and to the manufacturers,vhose products are represented, for their help by freely giving of the data used in this paper. In preparing the laterial used in this thesis, it was the authors at: to point out new develop-ants on existing instruments and recent inventions or engineer- ing equipment used principally by the Civil Engineer. 20 6052 TAEEE OF CONTENTS Chapter One Page Introduction B. Drafting Equipment ----------------------- 13 Chapter Two Telescopic Inprovenents A. Glass Reticles .......................... -32 B. Coated Lenses .......................... --J.B Chapter three The Tilting Level- ............................ -33 Chapter rear The First One-Second.Anerican Optical 28 “00d011 ‘6- -------------------------- e- --------- Chapter rive Chapter Six The Latest Type Altineter ----- - ................ 5.5 TABLE OF CONTENTS , Chapter Seven Page The Most Recent Drafting Machine ........... -39.--- Chapter Eight Chapter Nine SmOnnB By Radar ....... - ------------------ In”.-- Chapter Ten Conclusion ------------ - ----- -. -

MODULE 5 – Measuring Tools
INTRODUCTION TO MACHINING 2. MEASURING TOOLS AND PROCESSES: In this chapter we will only look at those instruments which would typically be used during and at the end of a fabrication process. Such instruments would be capable of measuring up to 4 decimal places in the inch system and up to 3 decimal places in the metric system. Higher precision is normally not required in shop settings. The discrimination of a measuring instrument is the number of “segments” to which it divides the basic unit of length it is using for measurement. As a rule of thumb: the discrimination of the instrument should be ~10 times finer than the dimension specified. For example if a dimension of 25.5 [mm] is specified, an instrument that is capable of measuring to 0.01 or 0.02 [mm] should be used; if the specified dimension is 25.50 [mm], then the instrument’s discrimination should be 0.001 or 0.002 [mm]. The tools discussed here can be divided into 2 categories: direct measuring tools and indirect measuring or comparator tools. 50 INTRODUCTION TO MACHINING 2.1 Terminology: Accuracy: can have two meanings: it may describe the conformance of a specific dimension with the intended value (e.g.: an end-mill has a specific diameter stamped on its shank; if that value is confirmed by using the appropriate measuring device, then the end-mill diameter is said to be accurate). Accuracy may also refer to the act of measuring: if the machinist uses a steel rule to verify the diameter of the end-mill, then the act of measuring is not accurate. -

1. Hand Tools 3. Related Tools 4. Chisels 5. Hammer 6. Saw Terminology 7. Pliers Introduction
1 1. Hand Tools 2. Types 2.1 Hand tools 2.2 Hammer Drill 2.3 Rotary hammer drill 2.4 Cordless drills 2.5 Drill press 2.6 Geared head drill 2.7 Radial arm drill 2.8 Mill drill 3. Related tools 4. Chisels 4.1. Types 4.1.1 Woodworking chisels 4.1.1.1 Lathe tools 4.2 Metalworking chisels 4.2.1 Cold chisel 4.2.2 Hardy chisel 4.3 Stone chisels 4.4 Masonry chisels 4.4.1 Joint chisel 5. Hammer 5.1 Basic design and variations 5.2 The physics of hammering 5.2.1 Hammer as a force amplifier 5.2.2 Effect of the head's mass 5.2.3 Effect of the handle 5.3 War hammers 5.4 Symbolic hammers 6. Saw terminology 6.1 Types of saws 6.1.1 Hand saws 6.1.2. Back saws 6.1.3 Mechanically powered saws 6.1.4. Circular blade saws 6.1.5. Reciprocating blade saws 6.1.6..Continuous band 6.2. Types of saw blades and the cuts they make 6.3. Materials used for saws 7. Pliers Introduction 7.1. Design 7.2.Common types 7.2.1 Gripping pliers (used to improve grip) 7.2 2.Cutting pliers (used to sever or pinch off) 2 7.2.3 Crimping pliers 7.2.4 Rotational pliers 8. Common wrenches / spanners 8.1 Other general wrenches / spanners 8.2. Spe cialized wrenches / spanners 8.3. Spanners in popular culture 9. Hacksaw, surface plate, surface gauge, , vee-block, files 10. -

CVP-19: Procedures for the Checking of Critical Dimensions of The
OMR-CVP-19 PROCEDURES FOR THE CHECKING OF CRITICAL DIMENSIONS OF THE CONICAL MOLD AND TAMPER AND THE CALIBRATION OF PYCNOMETERS AASHTO T 84 A. PURPOSE These procedures are intended to provide instruction for the verification of critical dimensions of the conical mold and tamper. B. APPARATUS REQUIRED 1. Calibrated calipers readable to 0.001 inch (.025 mm) 2. Calibrated balance capable of weighing 500 grams and readable to 0.1 gram. 3. Straightedge or ruler. 4. Thermometer readable to 0.1 °F or 0.1 °C. C. PROCEDURE Conical Cone 1. Measure the inside diameter of the top of the conical cone to the nearest 0.001 inch (.025 mm) by taking two (2) readings 90° apart with calipers and record results. 2. Invert cone and repeat Step 1 and record. 3. Place cone on a flat glass plate. Measure and determine the height of the cone by using the calipers and a straightedge and record results. 4. Measure and record the thickness of the cone to the nearest 0.001inch (.025 mm) with calipers by taking two (2) readings 90° apart on the top and bottom of cone. Tamper 1. Measure diameter of face of tamper by taking two (2) readings 90° apart. 2. Weigh and record weight of tamper to nearest 0.1 gram. Pycnometers Volumetric Flask (500 cm) calibrated annually at 21.3 °C – 24.7 °C (70.4 °F – 76.4 °F) by the following procedure: 1. Volumetric flasks are weighed empty and recorded to the nearest 0.1 gram. 2. Volumetric flasks are filled with water to the mark at which it is calibrated. -

FIELD EXTENSIONS and the CLASSICAL COMPASS and STRAIGHT-EDGE CONSTRUCTIONS 1. Introduction to the Classical Geometric Problems 1
FIELD EXTENSIONS AND THE CLASSICAL COMPASS AND STRAIGHT-EDGE CONSTRUCTIONS WINSTON GAO Abstract. This paper will introduce the reader to field extensions at a rudi- mentary level and then pursue the subject further by looking to its applications in a discussion of some constructibility issues in the classical straight-edge and compass problems. Field extensions, especially their degrees are explored at an introductory level. Properties of minimal polynomials are discussed to this end. The paper ends with geometric problems and the construction of polygons which have their proofs in the roots of field theory. Contents 1. introduction to the classical geometric problems 1 2. fields, field extensions, and preliminaries 2 3. geometric problems 5 4. constructing regular polygons 8 Acknowledgments 9 References 9 1. Introduction to the Classical Geometric Problems One very important and interesting set of problems within classical Euclidean ge- ometry is the set of compass and straight-edge questions. Basically, these questions deal with what is and is not constructible with only an idealized ruler and compass. The ruler has no markings (hence technically a straight-edge) has infinite length, and zero width. The compass can be extended to infinite distance and is assumed to collapse when lifted from the paper (a restriction that we shall see is irrelevant). Given these, we then study the set of constructible elements. However, while it is interesting to note what kinds objects we can create, it is far less straight forward to show that certain objects are impossible to create with these tools. Three famous problems that we will investigate will be the squaring the circle, doubling the cube, and trisecting an angle. -

Verification Regulation of Steel Ruler
ITTC – Recommended 7.6 - 02- 01 Procedures and Guidelines Page 1 of 7 Sample Work Instructions Effective Date Revision 2002 00 Calibration of Steel Rulers Table of Contents PURPOSE…………………………………...2 Edges………………………………….4 3.5.1 Requirements ...............................4 WORK INSTRUCTION……………………2 3.5.2 Method of Calibration..................4 3.6 Thickness of the Side Edge………….5 1 Introduction…………………………2 3.6.1 Method of Calibration..................5 2 Items and Condition of Calibration…..2 3.7 Arc Radius at the Intersecting Position of the End and the Side 3 Technical Requirements and Calibration Edges………………………………….5 Method……………………………………….2 3.7.1 Requirements ...............................5 3.1 Exterior………………………………2 3.7.2 Method Calibration......................5 3.1.1 Requirements ...............................2 3.8 Width and Difference Between the 3.2 Flatness of ruler face………………..3 Lines…………………………………..5 3.2.1 Requirements ...............................3 3.8.1 Requirements ...............................5 3.2.2 Method of Calibration..................4 3.8.2 Method of Calibration..................5 3.3 Elasticity……………………………..4 3.9 Error of Indication…………………..5 3.3.1 Requirements ...............................4 3.9.1 Requirements ...............................5 3.3.2 Method of Calibration..................4 3.9.2 Method of Calibration..................6 3.4 Linearity of the Ruler End and Side 4 Treatment of the Calibration Result and Edges………………………………….4 the Calibration Period………………….7 3.4.1 Requirements ...............................4