DOCSLIB.ORG

Flexible Modelling of Serial Correlation in GLMM

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Flexible Modelling of Serial Correlation in GLMM Flexible Modelling of Serial Correlation in GLMM Modellazione flessibile della struttura di correlazione seriale nei GLMM Mariangela Sciandra Dipartimento di Scienze Statistiche e Matematiche “Silvio Vianelli”, Universita` degli Studi di Palermo e-mail: [email protected] Keywords: longitudinal data, glmm, serial correlation, fractional polynomials 1. Introduction Mixed models have rapidly become a very useful tool for modelling longitudinal data because, thanks to their flexibility, they are particularly suited to handle many complex situations, especially when extensions like Generalized Linear or Nonlinear mixed models are used. However, existing works on Generalized Linear Mixed Models (GLMMs) assume the correlation between measurements on the same observational unit to be modelled only by the random effects while conditionally upon them the repeated measurements are assumed to be independent. Yet, it could happen that part of an individual observed profile may be a response to time-varying stochastic processes operating within that unit. This type of random variation results in a correlation between pairs of measurements on the same subject, called serial correlation, which is usually a decreasing function of the time separation between these measurements. So, in presence of serially correlated observations the functional specification of the covariance structure should be done through the simultaneous specification of the covariance structure induced by the random effects, which is typically non-stationary, and the specification of a “residual” component which accounts for deviations of the observations from the individual profiles. Standard GLMMs are not able to deal with serially correlated observations because assuming conditional independence they ignore correlation at the residuals level resulting in invalid inferences for the parameters in the mean structure of the model. In this work a general approach will be proposed consisting in extending to the GLMMs case the procedure proposed by Lesaffre et al. (1999) in the context of Linear Mixed Models (LMMs), for a flexible modelling of the GLMMs covariance structures as a combination of a parametric modelling of the random effects part with a flexible modelling of the serial correlation component through the use of Fractional Polynomials. 2. GLMMs for serially correlated observations Let Yij be the jth measurement for subject i, i = 1,...,m, j = 1,...,ni and Yi the ni-dimensional vector of all measurements taken on subject i, a GLMM assumes that, conditionally on q-dimensional random effects bi, the elements Yij of Yi are independent. The basis for the development of a Generalized Linear Mixed Model with autocorrelation is the decomposition xT zT b Yij = µij + ǫij = h( ijβ + ij i)+ ǫij where h(·) is the inverse of the link function, and the error terms have an appropriate distribution with variance equal to V ar(Yij|bi) = φv(µij) for v(·) the usual variance function in the exponential family. Then, using a Penalized Quasi-Likelihood (PQL) approach to the estimation, the GLMM is estimated by defining at each step a working variate Y∗ as a Taylor expansion of the response around the conditional mean evaluated i ˆ ˆ on the current estimates β and bi of fixed and random effects, respectively. The working Y∗ variate i of the specified GLMM then it is known (Schall, 1991) to be Y∗ ′ Y ˆ X ˆ Z bˆ ′ Y ˆ X Z b ∗ i ≡ g(ˆµi)+ g (ˆµi)( i − µi)= iβ + i i + g (ˆµi)( i − µi) ≈ iβ + i i + ǫi ∗ ′ where ǫi is equal to g (ˆµi)ǫi, which has also mean zero ∀i = 1, 2,...,m. Then E[Y∗|b] = Xβ + Zb and var(Y∗|b) = ∆Σ∆T where ∆ is the diagonal matrix ′ with diagonal entries g (ˆµi) and Σ = var(Y − µˆ). We can express the variance function Σ so that 1 1 1 1 2 A 2 H A 2 2 V ar(ǫi) = Φ i i i Φ (1) where Φ is a diagonal matrix with the over dispersion parameters along the diagonal, Hi is the correlation matrix and Ai is a diagonal matrix containing the variances following from the generalized linear model specification of Yij given the random effects bi. Using equation (1) we have the following expression for the marginal variance covariance matrix: 1 1 ∗ 1 1 Y V ZDZT 2 A 2 H A 2 2 var( )= = + Φ i i i Φ . That is, the working variate Y∗ takes the form of a weighted LMM with diagonal weight ˆ A−1 ′ −2 matrix W = µˆ [g (ˆµ)] . Then an iterative algorithm like that proposed by Schall (1991), in which a LMM is fitted to get estimates of β and b, is used. The use of this estimation algorithm allows us to introduce autocorrelation at the level of the linear Y∗ predictor in modelling the pseudo-variable i at each step trough a LMM or to define an autocorrelation function on the residuals evaluated at each step of the iterative process. Doing so, we can take advantage of the well-established correlation structures for LMMs. In particular, our proposal consists in modelling the serial correlation part using Fractional Polynomials (Royston and Altman, 1994) which allow the autocorrelation function g(·) in Hi to have a parametric form which is flexible enough to assume several shapes. This approach is very general and applies to all link function. Yet, it is important to underline how the estimate of the autocorrelation parameter obtained using this approach has to be considered only as an approximation of the underlying correlation structure of the observed data given by the correlation of its working variate. References Lesaffre E., Todem D., Verbeke G. (2000) Flexible modelling of the covariance matrix in a linear random effects model, Biometrical Journal, 42, 807–822. Royston P., Altman D. G. (1994) Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling, Applied Statistics, 43, 429–468. Schall R. (1991) Estimation in generalized linear models with random effects, Biometrika, 78, 719-727..
Load more

Recommended publications
  • Generalized Linear Models (Glms)
    San Jos´eState University Math 261A: Regression Theory & Methods Generalized Linear Models (GLMs) Dr. Guangliang Chen This lecture is based on the following textbook sections: • Chapter 13: 13.1 – 13.3 Outline of this presentation: • What is a GLM? • Logistic regression • Poisson regression Generalized Linear Models (GLMs) What is a GLM? In ordinary linear regression, we assume that the response is a linear function of the regressors plus Gaussian noise: 0 2 y = β0 + β1x1 + ··· + βkxk + ∼ N(x β, σ ) | {z } |{z} linear form x0β N(0,σ2) noise The model can be reformulate in terms of • distribution of the response: y | x ∼ N(µ, σ2), and • dependence of the mean on the predictors: µ = E(y | x) = x0β Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University3/24 Generalized Linear Models (GLMs) beta=(1,2) 5 4 3 β0 + β1x b y 2 y 1 0 −1 0.0 0.2 0.4 0.6 0.8 1.0 x x Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University4/24 Generalized Linear Models (GLMs) Generalized linear models (GLM) extend linear regression by allowing the response variable to have • a general distribution (with mean µ = E(y | x)) and • a mean that depends on the predictors through a link function g: That is, g(µ) = β0x or equivalently, µ = g−1(β0x) Dr. Guangliang Chen | Mathematics & Statistics, San Jos´e State University5/24 Generalized Linear Models (GLMs) In GLM, the response is typically assumed to have a distribution in the exponential family, which is a large class of probability distributions that have pdfs of the form f(x | θ) = a(x)b(θ) exp(c(θ) · T (x)), including • Normal - ordinary linear regression • Bernoulli - Logistic regression, modeling binary data • Binomial - Multinomial logistic regression, modeling general cate- gorical data • Poisson - Poisson regression, modeling count data • Exponential, Gamma - survival analysis Dr.
    [Show full text]
  • Bayesian Inference Chapter 4: Regression and Hierarchical Models
    Bayesian Inference Chapter 4: Regression and Hierarchical Models Conchi Aus´ınand Mike Wiper Department of Statistics Universidad Carlos III de Madrid Master in Business Administration and Quantitative Methods Master in Mathematical Engineering Conchi Aus´ınand Mike Wiper Regression and hierarchical models Masters Programmes 1 / 35 Objective AFM Smith Dennis Lindley We analyze the Bayesian approach to fitting normal and generalized linear models and introduce the Bayesian hierarchical modeling approach. Also, we study the modeling and forecasting of time series. Conchi Aus´ınand Mike Wiper Regression and hierarchical models Masters Programmes 2 / 35 Contents 1 Normal linear models 1.1. ANOVA model 1.2. Simple linear regression model 2 Generalized linear models 3 Hierarchical models 4 Dynamic models Conchi Aus´ınand Mike Wiper Regression and hierarchical models Masters Programmes 3 / 35 Normal linear models A normal linear model is of the following form: y = Xθ + ; 0 where y = (y1;:::; yn) is the observed data, X is a known n × k matrix, called 0 the design matrix, θ = (θ1; : : : ; θk ) is the parameter set and follows a multivariate normal distribution. Usually, it is assumed that: 1 ∼ N 0 ; I : k φ k A simple example of normal linear model is the simple linear regression model T 1 1 ::: 1 where X = and θ = (α; β)T . x1 x2 ::: xn Conchi Aus´ınand Mike Wiper Regression and hierarchical models Masters Programmes 4 / 35 Normal linear models Consider a normal linear model, y = Xθ + . A conjugate prior distribution is a normal-gamma distribution:
    [Show full text]
  • Bayesian Methods: Review of Generalized Linear Models
    Bayesian Methods: Review of Generalized Linear Models RYAN BAKKER University of Georgia ICPSR Day 2 Bayesian Methods: GLM [1] Likelihood and Maximum Likelihood Principles Likelihood theory is an important part of Bayesian inference: it is how the data enter the model. • The basis is Fisher’s principle: what value of the unknown parameter is “most likely” to have • generated the observed data. Example: flip a coin 10 times, get 5 heads. MLE for p is 0.5. • This is easily the most common and well-understood general estimation process. • Bayesian Methods: GLM [2] Starting details: • – Y is a n k design or observation matrix, θ is a k 1 unknown coefficient vector to be esti- × × mated, we want p(θ Y) (joint sampling distribution or posterior) from p(Y θ) (joint probabil- | | ity function). – Define the likelihood function: n L(θ Y) = p(Y θ) | i| i=1 Y which is no longer on the probability metric. – Our goal is the maximum likelihood value of θ: θˆ : L(θˆ Y) L(θ Y) θ Θ | ≥ | ∀ ∈ where Θ is the class of admissable values for θ. Bayesian Methods: GLM [3] Likelihood and Maximum Likelihood Principles (cont.) Its actually easier to work with the natural log of the likelihood function: • `(θ Y) = log L(θ Y) | | We also find it useful to work with the score function, the first derivative of the log likelihood func- • tion with respect to the parameters of interest: ∂ `˙(θ Y) = `(θ Y) | ∂θ | Setting `˙(θ Y) equal to zero and solving gives the MLE: θˆ, the “most likely” value of θ from the • | parameter space Θ treating the observed data as given.
    [Show full text]
  • Generalized Linear Models
    Generalized Linear Models A generalized linear model (GLM) consists of three parts. i) The first part is a random variable giving the conditional distribution of a response Yi given the values of a set of covariates Xij. In the original work on GLM’sby Nelder and Wedderburn (1972) this random variable was a member of an exponential family, but later work has extended beyond this class of random variables. ii) The second part is a linear predictor, i = + 1Xi1 + 2Xi2 + + ··· kXik . iii) The third part is a smooth and invertible link function g(.) which transforms the expected value of the response variable, i = E(Yi) , and is equal to the linear predictor: g(i) = i = + 1Xi1 + 2Xi2 + + kXik. ··· As shown in Tables 15.1 and 15.2, both the general linear model that we have studied extensively and the logistic regression model from Chapter 14 are special cases of this model. One property of members of the exponential family of distributions is that the conditional variance of the response is a function of its mean, (), and possibly a dispersion parameter . The expressions for the variance functions for common members of the exponential family are shown in Table 15.2. Also, for each distribution there is a so-called canonical link function, which simplifies some of the GLM calculations, which is also shown in Table 15.2. Estimation and Testing for GLMs Parameter estimation in GLMs is conducted by the method of maximum likelihood. As with logistic regression models from the last chapter, the generalization of the residual sums of squares from the general linear model is the residual deviance, Dm 2(log Ls log Lm), where Lm is the maximized likelihood for the model of interest, and Ls is the maximized likelihood for a saturated model, which has one parameter per observation and fits the data as well as possible.
    [Show full text]
  • Heteroscedastic Errors
    Heteroscedastic Errors ◮ Sometimes plots and/or tests show that the error variances 2 σi = Var(ǫi ) depend on i ◮ Several standard approaches to fixing the problem, depending on the nature of the dependence. ◮ Weighted Least Squares. ◮ Transformation of the response. ◮ Generalized Linear Models. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Weighted Least Squares ◮ Suppose variances are known except for a constant factor. 2 2 ◮ That is, σi = σ /wi . ◮ Use weighted least squares. (See Chapter 10 in the text.) ◮ This usually arises realistically in the following situations: ◮ Yi is an average of ni measurements where you know ni . Then wi = ni . 2 ◮ Plots suggest that σi might be proportional to some power of 2 γ γ some covariate: σi = kxi . Then wi = xi− . Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Variances depending on (mean of) Y ◮ Two standard approaches are available: ◮ Older approach is transformation. ◮ Newer approach is use of generalized linear model; see STAT 402. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Transformation ◮ Compute Yi∗ = g(Yi ) for some function g like logarithm or square root. ◮ Then regress Yi∗ on the covariates. ◮ This approach sometimes works for skewed response variables like income; ◮ after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. ◮ See page 130ff and check under transformations and Box-Cox in the index. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Generalized Linear Models ◮ Transformation uses the model T E(g(Yi )) = xi β while generalized linear models use T g(E(Yi )) = xi β ◮ Generally latter approach offers more flexibility.
    [Show full text]
  • Generalized Linear Models
    CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone.
    [Show full text]
  • Generalized Linear Models
    Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608) Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions • So far we've seen two canonical settings for regression. Let X 2 Rp be a vector of predictors. In linear regression, we observe Y 2 R, and assume a linear model: T E(Y jX) = β X; for some coefficients β 2 Rp. In logistic regression, we observe Y 2 f0; 1g, and we assume a logistic model (Y = 1jX) log P = βT X: 1 − P(Y = 1jX) • What's the similarity here? Note that in the logistic regression setting, P(Y = 1jX) = E(Y jX). Therefore, in both settings, we are assuming that a transformation of the conditional expec- tation E(Y jX) is a linear function of X, i.e., T g E(Y jX) = β X; for some function g. In linear regression, this transformation was the identity transformation g(u) = u; in logistic regression, it was the logit transformation g(u) = log(u=(1 − u)) • Different transformations might be appropriate for different types of data. E.g., the identity transformation g(u) = u is not really appropriate for logistic regression (why?), and the logit transformation g(u) = log(u=(1 − u)) not appropriate for linear regression (why?), but each is appropriate in their own intended domain • For a third data type, it is entirely possible that transformation neither is really appropriate. What to do then? We think of another transformation g that is in fact appropriate, and this is the basic idea behind a generalized linear model 1.2 Generalized linear models • Given predictors X 2 Rp and an outcome Y , a generalized linear model is defined by three components: a random component, that specifies a distribution for Y jX; a systematic compo- nent, that relates a parameter η to the predictors X; and a link function, that connects the random and systematic components • The random component specifies a distribution for the outcome variable (conditional on X).
    [Show full text]
  • Generalized Linear Models Outperform Commonly Used Canonical Analysis in Estimating Spatial Structure of Presence/Absence Data
    Generalized Linear Models outperform commonly used canonical analysis in estimating spatial structure of presence/absence data Lélis A. Carlos-Júnior1,2,3, Joel C. Creed4, Rob Marrs2, Rob J. Lewis5, Timothy P. Moulton4, Rafael Feijó-Lima1,6 and Matthew Spencer2 1 Programa de Pós-Graduacão¸ em Ecologia e Evolucão,¸ Universidade do Estado do Rio do Janeiro, Rio de Janeiro, Brazil 2 School of Environmental Sciences, University of Liverpool, Liverpool, United Kingdom 3 Departamento de Biologia, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil 4 Departamento de Ecologia, Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil 5 Department of Forest Genetics and Biodiversity, Norwegian Institute of Bioeconomy Research, Bergen, Nor- way 6 Division of Biological Sciences, University of Montana, Missoula, MT, United States of America ABSTRACT Background. Ecological communities tend to be spatially structured due to environ- mental gradients and/or spatially contagious processes such as growth, dispersion and species interactions. Data transformation followed by usage of algorithms such as Redundancy Analysis (RDA) is a fairly common approach in studies searching for spatial structure in ecological communities, despite recent suggestions advocating the use of Generalized Linear Models (GLMs). Here, we compared the performance of GLMs and RDA in describing spatial structure in ecological community composition data. We simulated realistic presence/absence data typical of many β-diversity studies. For model selection we used standard methods commonly used in most studies involving RDA and GLMs. Submitted 19 November 2018 Methods. We simulated communities with known spatial structure, based on three Accepted 30 July 2020 real spatial community presence/absence datasets (one terrestrial, one marine and Published 3 September 2020 one freshwater).
    [Show full text]
  • Generalized Linear Models I
    Statistics 203: Introduction to Regression and Analysis of Variance Generalized Linear Models I Jonathan Taylor - p. 1/18 Today's class ● Today's class ■ Logistic regression. ● Generalized linear models ● Binary regression example ■ ● Binary outcomes Generalized linear models. ● Logit transform ■ ● Binary regression Deviance. ● Link functions: binary regression ● Link function inverses: binary regression ● Odds ratios & logistic regression ● Link & variance fns. of a GLM ● Binary (again) ● Fitting a binary regression GLM: IRLS ● Other common examples of GLMs ● Deviance ● Binary deviance ● Partial deviance tests 2 ● Wald χ tests - p. 2/18 Generalized linear models ● Today's class ■ All models we have seen so far deal with continuous ● Generalized linear models ● Binary regression example outcome variables with no restriction on their expectations, ● Binary outcomes ● Logit transform and (most) have assumed that mean and variance are ● Binary regression ● Link functions: binary unrelated (i.e. variance is constant). regression ● Link function inverses: binary ■ Many outcomes of interest do not satisfy this. regression ● Odds ratios & logistic ■ regression Examples: binary outcomes, Poisson count outcomes. ● Link & variance fns. of a GLM ● Binary (again) ■ A Generalized Linear Model (GLM) is a model with two ● Fitting a binary regression GLM: IRLS ingredients: a link function and a variance function. ● Other common examples of GLMs ◆ The link relates the means of the observations to ● Deviance ● Binary deviance predictors: linearization ● Partial deviance tests 2 ◆ ● Wald χ tests The variance function relates the means to the variances. - p. 3/18 Binary regression example ● Today's class ■ A local health clinic sent fliers to its clients to encourage ● Generalized linear models ● Binary regression example everyone, but especially older persons at high risk of ● Binary outcomes ● Logit transform complications, to get a flu shot in time for protection against ● Binary regression ● Link functions: binary an expected flu epidemic.
    [Show full text]
  • Generalized Linear Models Link Function the Logistic Equation Is
    Newsom Psy 525/625 Categorical Data Analysis, Spring 2021 1 Generalized Linear Models Link Function The logistic equation is stated in terms of the probability that Y = 1, which is π, and the probability that Y = 0, which is 1 - π. π ln =αβ + X 1−π The left-hand side of the equation represents the logit transformation, which takes the natural log of the ratio of the probability that Y is equal to 1 compared to the probability that it is not equal to one. As we know, the probability, π, is just the mean of the Y values, assuming 0,1 coding, which is often expressed as µ. The logit transformation could then be written in terms of the mean rather than the probability, µ ln =αβ + X 1− µ The transformation of the mean represents a link to the central tendency of the distribution, sometimes called the location, one of the important defining aspects of any given probability distribution. The log transformation represents a kind of link function (often canonical link function)1 that is sometimes given more generally as g(.), with the letter g used as an arbitrary name for a mathematical function and the use of the “.” within the parentheses to suggest that any variable, value, or function (the argument) could be placed within. For logistic regression, this is known as the logit link function. The right hand side of the equation, α + βX, is the familiar equation for the regression line and represents a linear combination of the parameters for the regression. The concept of this logistic link function can generalized to any other distribution, with the simplest, most familiar case being the ordinary least squares or linear regression model.
    [Show full text]
  • Analysis of Bayesian Generalized Linear Models on the Number of Tuberculosis Patients in Indonesia with R
    Analysis of Bayesian Generalized Linear Models on the Number of Tuberculosis Patients in Indonesia with R Femmy Diwidian1, *, Anang Kurnia2, Kusman Sadik2 {[email protected]} 1 Mathematics Education Study Program , UIN Syarif Hidayatullah Jakarta , 15419, Indonesia 2 Statistics Department, Bogor Agricultural University , Bogor , 16680, Indonesia Abstract. Generalized Linear Models (GLM) is an extension of the linear regression model that aims to determine the causal relationship, the effect of independent variables on the dependent variable where the response variable is a member of the exponential family. In general, estimating parameters on GLM can be divided into two approaches, namely the frequentist method and the Bayesian GLM method. In this study, both approaches will be used to analyze the number of people suffering from tuberculosis in 34 provinces in Indonesia. The data used is based on 2018 Indonesia Health Profile Data and Information published by the Ministry of Health of the Republic of Indonesia in 2018. Based on the best model test criteria, this study provides results that the frequentist approach to GLM is better in matching the number of people suffering from tuberculosis in Indonesia compared to use Bayesian GLM. Keywords: Generalized Linear Models (GLM), Frequentis Method, Bayesian GLM Method 1. Introduction Generalized linear model (GLM) is an extension of the linear regression model assuming the predictor has a linear effect but does not assume a particular distribution of the response variable and is used when the response variable is a member of an exponential family [1]. GLM aims to determine the causal relationship, the effect of independent variables on the dependent variable.
    [Show full text]
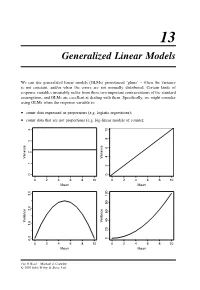
  • Generalized Linear Models
    13 Generalized Linear Models We can use generalized linear models (GLMs) pronounced ‘glims’ – when the variance is not constant, and/or when the errors are not normally distributed. Certain kinds of response variables invariably suffer from these two important contraventions of the standard assumptions, and GLMs are excellent at dealing with them. Specifically, we might consider using GLMs when the response variable is: • count data expressed as proportions (e.g. logistic regressions); • count data that are not proportions (e.g. log-linear models of counts); 10 8 6 Variance Variance 24 01234 0 0246810 0246810 Mean Mean 2.0 3.0 Variance Variance 1.0 020406080100 0.0 0246810 0246810 Mean Mean The R Book Michael J. Crawley © 2007 John Wiley & Sons, Ltd 512 THE R BOOK • binary response variables (e.g. dead or alive); • data on time to death where the variance increases faster than linearly with the mean (e.g. time data with gamma errors). The central assumption that we have made up to this point is that variance was constant (top left-hand graph). In count data, however, where the response variable is an integer and there are often lots of zeros in the dataframe, the variance may increase linearly with the mean (top tight). With proportion data, where we have a count of the number of failures of an event as well as the number of successes, the variance will be an inverted U-shaped function of the mean (bottom left). Where the response variable follows a gamma distribution (as in time-to-death data) the variance increases faster than linearly with the mean (bottom right).
    [Show full text]