DOCSLIB.ORG

Crosspolarization and Depolarization in Ellipsometry at Inner Boundaries

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Crosspolarization and Depolarization in Ellipsometry at Inner Boundaries Crosspolarization and Depolarization in Ellipsometry at Inner Boundaries • Introduction and Motivation • In optics we never measure the fields! • Decoherence • Temporal and Spatial • Depolarization • Temporal • Depolarization Kurt Hingerl & Razvigor Ossikovski • Spatial University Linz & Ecole Polytechnique • Summary [email protected] Opt. Lett. 41, 219, (2016), Opt. Lett. 41, 4044, (2016), Paul Dirac „Quantum Mechanics“: ~ 1935 “each photon then interferes only with itself. Interference between different photons never occurs.” Albert Einstein to his friend Michael Besso 1954: “All these fifty years of conscious brooding have brought me no nearer to the answer to the question, 'What are light quanta?' Nowadays every Tom, Dick and Harry thinks he knows it, but he is mistaken.” R. Feynman QED- the strange theory matter and light, 1985 When a photon comes down, it interacts with electrons throughout the glass, not just on the surface. The photon and electrons do some kind of dance, the net result of which is the same as if the photon hit only on the surface. W.E. Lamb 1995, Appl. Phys B “Photons cannot be localized in any meaningful manner, and they do not behave at all like particles, whether described by a wave function or not." Roy Glauber „Nobel lecture: Quantum Mechanics“: 2005 “….if we get a click in a detector, we know that at that very moment the photon is just there….” What does depolarization mean? Partial state of polarization produced by the interaction of polarized light and an optical element (depolarizer). Case 1 Case 2 Two phase system: semi-infinite material & air Totally polarized Depolarization E r 22s sin ( ) cos( ) sin ( ) Ei r pp a : tan ei Ersrs 2 2 sin ( ) cos( ) sin ( ) Ei s a Case 1: For nondepolarising system fully equivalent Mueller matrix formalism Jones formalism Sin Sout M Sout M Sin Ex v s MMMM s v out J v in 00 11 12 13 14 E y s MMMM s 11 21 22 23 24 . s MMMM s 22 31 32 33 34 out in s MMMM s E r r E 33out 41 42 43 44 in x pp ps x out r r in Ey sp ss Ey Degree of polarization (DOP) sss222 DOP123(0 DOP 1) Common states of polarization s 0 Degree of Depolarization () approximately ssss222 0 123 s 0 Totally polarized DOP = 1 Partially depolarizing case: Sin Sout M 0 < DOP < 1 Partially polarized light Sout M Sin Stokes vector JJ11 12 rrppps rrrr ppsspsss J rss sII0 I xy EExx EE yy rr rr 1 JJ21 22 sp ss sp ss sIIQ EE EE isotropic material S 1 xy xx yy sIIU EE EE r 0 2 45 45 xy yx pp 0 rss sII3 V GD iEEEE xy yx 2 2 2 2 2 2 1 2 1 2 * * * * 2 J pp J ss J sp J ps 2 J pp J ss J sp J ps ReJ ps J pp J ss J sp ImJ ps J pp J ss J sp 2 2 2 2 2 2 1 2 1 2 * * * * 2 J pp J ss J ps J sp 2 J ss J pp J sp J ps ReJ ps J pp J sp J ss Im J ps J pp J sp J ss M * * * * * * * * ReJ pp J sp J ps J ss ReJ pp J sp J ps J ss ReJ pp J ss J ps J sp Im J pp J ss J ps J sp Im J * J J * J Im J * J J * J Im J * J J * J Re J * J J * J pp sp ps ss pp sp ps ss pp ss ps sp pp ss ps sp Field amplitudes Ex, Ey are defined statistically: The Stokes vector components are linear combinations of the second moments of their joint probability distributions, which are directly related to the experimentally measurable intensities. E- field components oscillate ~ 10^(16)/s Experimental observations- Depolarization occurs: Surface scattering Incidence angle distribution Sample Sample Wavelength variation Backside reflection Thin film Sample Substrate Thickness inhomogeneity substrate Müller Matrix Ellipsometer Optical set up M M M M 11 12 13 14 M 21 M 22 M 23 M 24 . M M M M 31 32 33 34 M 41 M 42 M 43 M 44 1: Glan-Taylor polarizer 2: Quarterwave at 510nm ferroelectic liquid crystal cell 3: Zero order Quarter waveplate at 633nm 4: Halfwave at 510nm ferroelectric liquid crystal cell Decomposition of the Mueller matrix Experimental data Coherence matrix Lu Chipman Decomposition: Measured matrix decomposed in MΔ, MR and MD Depolarization X Retardance (Phase) X Diattanuation (preferred absorption of one linear polarization state) (not unique‐ what is the correct decomposition?) Non‐depolarizing Depolarizing Medium medium Decoherence We never measure in optics the fields, we always measure 2nd moments: ~ 1015 10 16s 1 ; fastest Detector ~ ps; at least 10 6 oszillations measured 2 2 11T /2 T /2 Inc0 lim Etdti () ExampleIK : lim EtEtdt12 () () T T TTT /2 i T /2 K Ert101(,) E cos( kr12 t12 ) Ert 202 (,) E cos( kr t ) 2 1 T /2 IKlim EtEtdt12 () () T T T /2 112 2 K E01 EEE02 01 02 cos( kkr12 ( )) 21 22 EE01 02 22 KE00 Ecos( k12 k r () ) 21 If phase is not well defined e.g. 0,2 => Statistical Optics! Temporal and Spatial Decoherence via Wiener Khitchin theorem (FT) 2 Photons (2 interfering beams) => N photons (N interfering beams) • Finite coherence length of your light source lµm 100 • Monochromator resolution ~ c ~3nm ~1013 s 1 • 1 Watt ~ 1019 photons/s, they all interfere, rather complicated beating pattern („purely?“ statistical?): N=100, 1 ps, 1 µs, 1 s Spectroscopic ellipsometry for a thick overlayer: Defined Incremental decoherence phase ()q r1 ()q rn ()qqq ()() ()qq () trt (1)i rr 01 12 10 ()qqq () () 001 rrr11012 a 2d in n11cos c o e s 500nm lnmµm ~ 500 100 in Air! ( refractive index goes in, too) c 3nm Decoherence 1 22 2cos()EE00 krkr12() 2 21 S D • Lets assume we have the most perfect sample in the world, with a „most“ homogeneous thickness: SiO2 on Si lµm 100 • Finite coherence length of your light source c • Monochromator resolution ~ ~3nm ~1013 s 1 • 1 Watt ~ 1019 photons/s, they all interfere, rather complicated beating pattern („purely?“ statistical?) • If 2‐1 is purely stochastic [, the measured intensity is just the sum of the intensities, all coherence lost! , Retardation: Ewald Oseen , Defined phase , r Incremental decoherence Ept () ,….., rad c , a ()qq () () q J 00rr 01 Jrtrtr()qqqqqqq () () ()() ()1 r ()2 2d 2d 2d 1 1 01 12 10 12 01 o 2 2 2 n1 cos1 n1 n0 sin 0 ()q () q () qqqqq () () ()() () q () qq () c c c J2 r 2 trrrt 01 12 10 12 10 r 1 rr 10 12 ()qqqqqqqq () () () () () () () 2 Jrrrrrrr33 2101211012 (,sp ) ( q ) ( q ) ( q ) ( q ) (1)i Jrrrrii11012 s Correlation functions in time ‐‐ ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ (,sp ) 2 IDn rEt01( ) rEt ( ) rEt 2 ( 2 ) .... rEt ( n ) 22 2 2 rEt01()()....() rEt rEtnnmn rEtmrEtn ( )() nm10 mn 2 2 rmn EtrEt() () rr mn EtEt () ( ( m n ) ) mnm010 mn , Correlation functions in time via Wiener Khitchin theorem (FT) , ,….., ‐‐ ‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐ , J JJJwd**;''';' kmt k m Assuming e.g. a monochromator resolution function (Gaussian, Lorentz, equal distribution) putsusin the position to evaluate each term and sum it: (')qq ()(')* q q Arrnm n m exp nm Im exp inm Re 2 1 ' rr()qq (')*exp nm Im exp exp i ' nm Re d ' nm 22 2 2 ()qq (')* 22 rrnm exp nm Im exp i nm Re exp nm Re[ ] 2 2 ()qq (')*2 2 () qq (')* G AnmAnmAAfexp Re nm nm 2 Convolution between a sample property and a measurement setup property (light source, monochromator & detector) Forward Simulation (all 16 MMs) of 10µmSiO/Si ( 3nm spectral width) M12 10 µm SiO2 on Si Normalized M(1,1) Sample assumed as perfectly homogeneous Temporal and Spatial Decoherence (quasimonochromatic) 22 EE0 0 cos(()kk1 2 r (21 )) 2 2 2 R 2 QA 2 ~50 µm s P Source 1 Can be proven: van Cittert – ext. Q Zernike Theorem sR Experiments: P2 Sun: 0.1 mm^2 Orion star: 6 m^2 Decoherence‐ angle distributions 22 EE0 0 cos(()kk1 2 r (21 )) S D • Lets assume quasicoherent radiation: • Then, the size of the source counts for interference at the screen: Transverse coherence area A 2 2 2 R 2 QA 2 ~50 µm s P Source 1 Can be proven: van Cittert – ext. Q Zernike Theorem sR Experiments: P2 Sun: 0.1 mm^2 Orion star: 6 m^2 Spatial Decoherence 22 EE00cos( krkr12 (21 )) S D • Lets assume quasicoherent radiation: • Then, the size of the source counts for interference at the screen: Transverse coherence area A 2 2 R 2 A 2 ~10µm s P Source 1 ext. Q WhysR is the measured depolarization so small? P2 Decoherence‐ some mathematics „Optical coherence and quantum optics“ L.Mandel and E. Wolf, Cam. UP (1995) „Statistical Optics“, Joseph W. Goodman, Wiley (2000) 1. Coherence length does not count „strongly“: “..the fields at P1 and P2, represented by equations (4.2‐ 10), will indeed be strongly correlated. Hence we see that, even though the two sources S1 and S2 are statistically independent, they give rise to correlations ..these correlations are generated in the process of propagation and superposition.” 2. Interference of two stationary light beams as a second‐order correlation phenomenon ErtP111112221(, ) KEStR ( , / c ) KEStR ( , / c ) * 2222 Ir( , t) E( r , tEr) ( , t) = K1 ES( 1 , t R 11/ c ) K 2 ES( 2 , t R 21 / c ) ** 2Re(KKE12 ( S 1 , t R 11/ cES ) ( 2 , t R 21/ c )) 22 * K1IStR( 1 , 11/) c K 2 IStR(, 2 21/) c 2Re( KK 1 2 )( SStttt 1 , 2 , 1 , 2 ) Spatial Decoherence 22 EE00cos( kkr12 (21 )) S D Spatial Correlation: Z Det 1.
Load more

Recommended publications
  • Optical Gyroscopes: Sensing Rotation Without Moving Parts Abstract
    Abstract The desire for accurate navigation has been one of the great technology drivers since ancient times. Astronomy, timekeeping, magnetic sensors, the GPS system, MEMs, and spinning- mass gyroscopes are all familiar methods to measure position. The sensing of rotation by Optical Gyroscopes: optical means was first demonstrated by Sagnac in 1913, and in 1925 Michelson and Gale measured the rotation of the Earth with a 2km loop interferometer. The Sagnac effect was relegated to being a physics curiosity, until the 1960s and the advent of the laser and optical Sensing Rotation fiber. One of the great achievements of navigation engineering was the harnessing of the Sagnac effect, to make practical and extremely sensitive yet rugged optical rotation sensors. Without Moving Parts The Sagnac effect is very small, and it is necessary to measure on the order of one part out of 1020 to reach high-accuracy requirements. The design and manufacturing of practical optical gyroscopes is a tour-de-force of physics and engineering. Basic concepts such as symmetry, relativity, and reciprocity, and considerable interdisciplinary effort are needed in order to create a design such that every perturbation cancels out except rotation. Optical gyroscopes, Robert Dahlgren and their research and production contracts, were an early driver for many ultra-high- performance optical technologies. Such commonplace items as low-scatter mirrors, ultrasonic Silicon Valley Photonics, Ltd. machining of glass, lithium niobate integrated optics, polarization-maintaining fiber, superluminescent and narrow-linewidth lasers found their first major applications and customers in these sensors. Presented to the IEEE SCV Preceding Image: Monolithic Ring Laser Gyro (MRLG).
    [Show full text]
  • Polarization (Waves)
    Polarization (waves) Polarization (also polarisation) is a property applying to transverse waves that specifies the geometrical orientation of the oscillations.[1][2][3][4][5] In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave.[4] A simple example of a polarized transverse wave is vibrations traveling along a taut string (see image); for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic [6] waves such as light and radio waves, gravitational waves, and transverse Circular polarization on rubber sound waves (shear waves) in solids. thread, converted to linear polarization An electromagnetic wave such as light consists of a coupled oscillating electric field and magnetic field which are always perpendicular; by convention, the "polarization" of electromagnetic waves refers to the direction of the electric field. In linear polarization, the fields oscillate in a single direction. In circular or elliptical polarization, the fields rotate at a constant rate in a plane as the wave travels. The rotation can have two possible directions; if the fields rotate in a right hand sense with respect to the direction of wave travel, it is called right circular polarization, while if the fields rotate in a left hand sense, it is called left circular polarization.
    [Show full text]
  • Stitching Type Large Aperture Depolarizer for Gas Monitoring Imaging Spectrometer
    The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLII-3, 2018 ISPRS TC III Mid-term Symposium “Developments, Technologies and Applications in Remote Sensing”, 7–10 May, Beijing, China STITCHING TYPE LARGE APERTURE DEPOLARIZER FOR GAS MONITORING IMAGING SPECTROMETER Xiaolin Liu*, Ming Li, Ning An, Tingcheng Zhang, Guili Cao, Shaoyuan Cheng Beijing Institute of Space Mechanics & Electricity, Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, China – (mojiexiaolin, 13521820892, anningji, tczhang1217, bitlitian,csycf) @163.com Commission III, WG III/8 KEY WORDS: Polarization, Depolarizer, Muller matrix, Imaging Spectrometer, Stitching, Numerical Analysis ABSTRACT: To increase the accuracy of radiation measurement for gas monitoring imaging spectrometer, it is necessary to achieve high levels of depolarization of the incoming beam. The preferred method in space instrument is to introduce the depolarizer into the optical system. It is a combination device of birefringence crystal wedges. Limited to the actual diameter of the crystal, the traditional depolarizer cannot be used in the large aperture imaging spectrometer (greater than 100mm). In this paper, a stitching type depolarizer is presented. The design theory and numerical calculation model for dual babinet depolarizer were built. As required radiometric accuracies of the imaging spectrometer with 250mm×46mm aperture, a stitching type dual babinet depolarizer was design in detail. Based on designing the optimum structural parmeters，the tolerance of wedge angle， refractive index, and central thickness were given. The analysis results show that the maximum residual polarization degree of output light from depolarizer is less than 2%. The design requirements of polarization sensitivity is satisfied. 1.
    [Show full text]
  • Longitudinal Polarization Periodicity of Unpolarized Light Passing Through a Double Wedge Depolarizer
    Longitudinal polarization periodicity of unpolarized light passing through a double wedge depolarizer 1 2, 3 Juan Carlos G. de Sande, Massimo Santarsiero, ∗ Gemma Piquero, and Franco Gori2 1Departamento de Circuitos y Sistemas, Universidad Polit´ecnica de Madrid, 28031 Madrid, Spain 2Dipartimento di Fisica, Universit`aRoma Tre, and CNISM, via della Vasca Navale 84, I-00146 Roma, Italy 3Departamento de Optica,´ Universidad Complutense de Madrid, 28040 Madrid, Spain ∗santarsiero@fis.uniroma3.it Abstract: The polarization characteristics of unpolarized light passing through a double wedge depolarizer are studied. It is found that the degree of polarization of the radiation propagating after the depolarizer is uniform across transverse planes after the depolarizer, but it changes from one plane to another in a periodic way giving, at different distances, unpolarized, partially polarized, or even perfectly polarized light. An experiment is performed to confirm this result. Measured values of the Stokes parameters and of the degree of polarization are in complete agreement with the theoretical predictions. © 2012 Optical Society of America OCIS codes: (260.5430) Polarization; (030.1640) Coherence (240.5440); Polarization- selective devices. References and links 1. J. P. McGuire and R. A. Chipman, “Analysis of spatial pseudodepolarizers in imaging systems,” Opt. Eng. 29, 1478–1484 (1990). 2. S. C. McClain, R. A. Chipman, and L. W. Hillman “Aberrations of a horizontal/vertical depolarizer,” Appl. Opt. 31, 2326–2331 (1992). 3. M. El Sherif, M.S. Khalil, S. Khodeir, and N. Nagib, “Simple depolarizers for spectrophotometric measurements of anisotropic samples,” Opt. & Laser Technol. 28, 561-563 (1996). 4. G. Biener, A. Niv, V. Kleiner, and E.
    [Show full text]
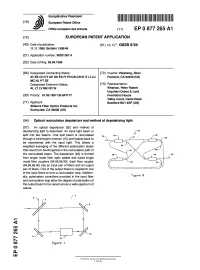
  • Optical Recirculaton Depolarizer and Method of Depolarizing Light
    Patentamt Europaisches ||| || 1 1| || || || || || || || || ||| || (19) J European Patent Office Office europeen des brevets (11) EP 0 877 265 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication:ation: (51) |nt. CI.6: G02B 6/34 11 .11 .1 998 Bulletin 1 998/46 (21) Application number: 98201367.4 (22) Date of filing: 28.04.1998 (84) Designated Contracting States: (72) Inventor: Paisheng, Shen AT BE CH CY DE DK ES Fl FR GB GR IE IT LI LU Fremont, CA 94539 (US) MCNLPTSE Designated Extension States: (74) Representative: AL LT LV MK RO SI Wharton, Peter Robert Urquhart-Dykes & Lord (30) Priority: 01.05.1997 US 847177 Inventions House Valley Court, Canal Road (71) Applicant: Bradford BD1 4SP (GB) Alliance Fiber Optics Products Inc. Sunnyvale, CA 94086 (US) (54) Optical recirculaton depolarizer and method of depolarizing light (57) An optical depolarizer (82) and method of depolarizing light is described. An input light beam is split into two beams. One split beam is recirculated 92 94-. through a birefringent medium (12) and looped back to ~\ ._ i — , f* be recombined with the input light. This allows a ( 7\ 96 weighted averaging of the different polarization states \ that result from birefringence in the recirculation path of ^"^^^ ^-uh the recirculated beam. The depolarizer (82) is formed as-. / from single mode fiber optic cables and fused single — v^c mode fiber couplers (84,86,88,90). Each fiber coupler f? ^"^-us (84,86,88,90) has an input pair of fibers and an output \l pair of fibers. One of the output fibers is coupled to one ^ — of the input fibers to form a recirculation loop.
    [Show full text]
  • Quartz-Wedge Achromatic Depolarizers
    Quartz-Wedge Achromatic Depolarizers http://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=870&pn... Search Search ( 0) $ Dollar ▼ ENGLISH ▼ Create an Account | Log In Products Home Rapid Order Services The Company Contact Us My Thorlabs >>Polarization Optics >>Polarizers >>Quartz-Wedge Achromatic Depolarizers Quartz-Wedge Achromatic Depolarizers Related Items ► Randomizes the Polarization of a Linearly Polarized Input Beam ► Effective with Monochromatic and Broadband Light ► Available with AR Coatings DPU-25-A DPU-25-C DPU-25-A Depolarizer DPU-25 DPU-25-B Mounted in an SM1 Lens Tube Overview Graphs Quartz vs. LCP Tutorial Damage Thresholds Documents Feedback Features General Specifications Optic Axis Alignment Not Required Substrate Quartz Crystal Ideal for Broadband Light Sources and Large Diameter (>6 mm) Monochromatic Beams Air-Gap Design Allows for use with High-Power Beams Uncoated (190 - 2500 nm) Available Uncoated (190 - 2500 nm) or with One of Three AR Coatings -A Coating (350 - 700 nm) Coatings 350 - 700 nm (-A Coating) -B Coating (650 - 1050 nm) 650 - 1050 nm (-B Coating) -C Coating (1050 - 1700 nm) 1050 - 1700 nm (-C Coating) Outer Diameter 1" (25.4 mm) Thorlabs' Quartz-Wedge Achromatic Depolarizers convert a polarized beam of light into a pseudo-random polarized beam of light. The term Thickness 7.35 mm (0.289") pseudo-random is used since the transmitted beam doesn't become unpolarized; instead the polarization of the beam is randomized. Linearly polarized light from a monochromatic source that is transmitted through a quartz-wedge depolarizer will have a polarization that varies spatially. Clear Aperture >Ø21.59 mm Linearly polarized light from a broadband source that is transmitted through a quartz-wedge depolarizer will have a polarization that varies spatially Surface Flatness λ/10 @ 633 nm as well as with wavelength.
    [Show full text]
  • Monochromatic Depolarizer Based on Liquid Crystal
    crystals Article Monochromatic Depolarizer Based on Liquid Crystal Paweł Mar´c* , Noureddine Bennis, Anna Spadło , Aleksandra Kalbarczyk , Rafał W˛egłowski, Katarzyna Garbat and Leszek R. Jaroszewicz Faculty of New Technologies and Chemistry, Military University of Technology, 2 gen. S. Kaliskiego St., 00-908 Warsaw, Poland * Correspondence: [email protected]; Tel.: +48-261-839-424 Received: 24 May 2019; Accepted: 22 July 2019; Published: 28 July 2019 Abstract: Polarization is a very useful parameter of a light beam in many optical measurements. Improvement of holographic systems requires optical elements which need a diffused and depolarized light beam. This paper describes a simple monochromatic depolarizer based on a pure vertically aligned liquid crystal without pretilt. In this work we present an extended description of depolarizer by analyzing its electro-optic properties measured in spatial and time domains with the use of crossed polarizers and polarimetric configurations. Crossed polarizers set-up provides information on spatial and temporal changes of microscopic textures while polarimetric measurement allows to measure voltage and time dependence of degree of polarization. Three different thicknesses, i.e., 5 µm, 10 µm and 15 µm have been manufactured in order to analyze another degree of freedom for this type of depolarizer device based on a liquid crystals’ material. Consideration of the light scattering capability of the cell is reported. Keywords: depolarization; liquid crystals; Mueller matrices 1. Introduction Depolarized light is very useful in optical measurements continuously finding application as for example spatial diffused phase element in holography [1]. Commercially used light sources are polarized or at least partially polarized.
    [Show full text]
  • Measuring Ultra-Low PMD with High Reliability
    VIAVI Solutions Application Note Measuring Ultra-Low PMD with High Reliability By Vincent Lecoeuche, PhD and Gregory Lietaert, Product Marketing Introduction Polarization mode dispersion (PMD) has concerned fiber/equipment manufacturers and service providers (Telco or multiple-system operators [MSOs]) for some time. However, increased transmission speeds and the related PMD-dependent limits have driven field measurement interests from identifying high-PMD values to performing reliable and repeatable high-resolution PMD measurements. The Requirements Advanced Fiber Specifications With every enhancement made over the past few years, fiber and cable manufacturers have significantly improved the performance of fiber and cabling designs and greatly reduced PMD. They have developed processes for manufacturing optical fibers with ultra low PMD. This ultra low PMD can further be preserved because of modern cabling design. Leading manufacturers now specify the Link Design Value (LDV), which could be less than 0.04 ps/√km, when the cable is installed in the field. Link Design Value1 LDV provides a useful design parameter for calculating the worst-case amount of PMD a fiber contributes toward the overall system PMD for a link. LDV, also referred to as PMDQ, is a term developed in standards bodies used to evaluate the impact of fiber-related PMD where cabled fibers are deployed in concatenated sections. The LDV is the worst-case PMD of the end-to-end link made up of randomly chosen cable sections spliced together and, therefore, represents the worst-case PMD of a fiber path in a deployed cable span. PMD standards suggest calculating LDV from nominally 20 to 24 sections with a maximum cumulative distribution Q of nominally 0.001 to 0.0001, which implies that 0.1 percent or 0.01 percent of all spans (made up of concatenated sections) would be above this level of PMD.
    [Show full text]
  • Epoxy Free Assemblies Optical Bonding Technology High Damage
    nqa ISO 9001 U K A S QUALITY R e g i s t e r e d MANAGEMENT 015 Epoxy Free Assemblies C A T Innovation Of High Power Optics Optical Bonding Technology A L O High Damage Threshold G 2 0 Crystals & Optical components 1 5 - 2 0 1 6 Dayoptics,Inc 6 Yangqi Branch 8 Jinshan Fuwan Park, Fuzhou, Fujian,350008,China Tel:+(86)591-83215681 Fax:+(86)591-83215359 E-mail:[email protected] www.dayoptics.com Dayoptronics Co.,Ltd 008,Jinshui West Road,Ningxiang High-tech Zone,Changsha,Hunan,410600,China Tel:+(86)731-87051588 Fax:+(86)731-87051788 E-mail:[email protected] COMPANY PROFILE THE COMPANY THE STRENGTH Dayoptics has been dedicated to serving the high power laser community during the past decade. Our complete line The extremely high quality, ultra-low cost, mass production, of High Power PBS, High Power Glan Laser Polarizers, and high power waveplates, etc, offer our customers just-in-time delivery and the satisfactory service are the key satisfactory one-stop shopping. Understand the high power laser application is the recent and future trend; our points which enable Dayoptics to go from strength to engineers keep on exploring new technologies to meet the increasing marketing demand. “ Innovation of high strength. power optics” is not just a slogan, but an action in our daily working. Based on rich production experience and strong engineering support, Dayoptics continuously creates innovative ideas for optics. MARKETPLACE As a manufacturer of crystal and optical products which are widely used in semiconductor, electronics, optics, laser and telecommunication, Dayoptics excels at manufacturing reliable high-quality products at very competitive prices.
    [Show full text]
  • Technical Digest: Symposium on Optical Fiber Measurements, 2004
    NIST Special Publication 1024 Technical Digest: Symposium on Optical Fiber Measurements, 2004 Sponsored by the National Institute of Standards and Technology in cooperation with the IEEE Lasers and Electro-Optics Society and the Optical Society of America NIST Special Publication 1024 Technical Digest: Symposium on Optical Fiber Measurements, 2002 Digest of a symposium sponsored by the National Institute of Standards and Technology in cooperation with the IEEE Lasers and Electro-Optical Society and the Optical Society of America September 28-30, 2004 National Institute of Standards and Technology Boulder, Colorado 80305 Edited by P. A. Williams G. W. Day September 2004 U.S. Department of Commerce Donald L. Evans, Secretary Technology Administration Phillip J. Bond, Under Secretaryfor Technology National Institute of Standards and Technology Arden L. Bement, Jr., Director National Institute of Standards and Technology Special Publication 1024 Natl. Inst. Stand. Technol. Spec. Publ. 1024, pages (September 2004) CODEN: NSPUE2 U.S. GOVERNMENT PRINTING OFFICE WASHINGTON: 2004 For sale by the Superintendent of Documents, U.S. Government Printing Office Internet: bookstore.gpo.gov Phone: (202) 512-1 800 Fax: (202) 5 1 2-2250 Mail: Stop SSOP, Washington, DC 20402-0001 PREFACE »0C!« ' Welcome to SOFM 2004, the quarter-of-a-century mark for this meeting that has taken place every other year since 1980. Since that time, SOFM has provided this glimpse of what's going on in the area of measurements relating to optoelectronics. This year, we again see a broad range of topics including wavelength metrology, nonlinear measurements, OTDR improvements, fiber index characterization, fiber Bragg grating measurement techniques, and PMD.
    [Show full text]
  • Application of Spectroscopic Ellipsometry and Mueller Ellipsometry to Optical Characterization E
    Application of Spectroscopic Ellipsometry and Mueller Ellipsometry to Optical Characterization E. Garcia-Caurel1, A. De Martino1, J-P. Gaston2, L.Yan3 1LPICM, CNRS-Ecole Polytechnique, Palaiseau, France 2HORIBA Scientific, Chilly-Mazarin, France 3HORIBA Scientific, Edison, NJ, USA This article aims to provide a brief overview of both established and novel ellipsometry techniques, as well as their applications. Ellipsometry is an indirect optical technique in that information about the physical properties of a sample is obtained through modeling analysis. Standard ellipsometry is typically used to characterize optically isotropic bulk and/or layered materials. More advanced techniques like Mueller ellipsometry, also known as polarimetry in literature, are necessary for the complete and accurate characterization of anisotropic and/or depolarizing samples which occur in many instances, both in research and “real life” activities. In this article we cover three main areas of subject: basic theory of polarization, standard ellipsometry and Mueller ellipsometry. Section I is devoted to a short and pedagogical introduction of the formalisms used to describe light polarization. The following section is devoted to standard ellipsometry. The focus is on the experimental aspects, including both pros and cons of commercially available instruments. Section III is devoted to recent advances in Mueller ellipsometry. Applications examples are provided in sections II and III to illustrate how each technique works. Keywords: Polarization; Ellipsometry; Thin Films; Mueller matrix INTRODUCTION The use of polarized light to characterize the optical properties of materials, either in bulk or thin film format, has enjoyed great success over the past decades. The different methods of generating and analyzing the polarization properties of light is traditionally called Ellipsometry.
    [Show full text]
  • Liquid Crystal Depolarizer Based on Photoalignment Technology
    70 Photon. Res. / Vol. 4, No. 2 / April 2016 Wei et al. Liquid crystal depolarizer based on photoalignment technology Bing-Yan Wei,1 Peng Chen,1 Shi-Jun Ge,1 Li-Chao Zhang,2 Wei Hu,1,* and Yan-Qing Lu1 1National Laboratory of Solid State Microstructures, Collaborative Innovation Center of Advanced Microstructures and College of Engineering and Applied Sciences, Nanjing University, Nanjing 210093, China 2Thorlabs China, Shanghai, 200331, China *Corresponding author: [email protected] Received February 4, 2016; revised February 23, 2016; accepted February 24, 2016; posted February 26, 2016 (Doc. ID 258959); published March 21, 2016 We propose a depolarizer based on the principle of a collection of half-wave plates with randomly distributed optic axes. The design is demonstrated by means of dynamically photopatterning liquid crystal into randomly aligned homogeneous domains. We characterize the liquid crystal depolarizer for 1550 nm and C-band (1520– 1610 nm). A degree of polarization of less than 5% is obtained for any linearly polarized light. This study provides a practical candidate for high-performance depolarizers. © 2016 Chinese Laser Press OCIS codes: (230.3720) Liquid-crystal devices; (260.5430) Polarization; (060.2390) Fiber optics, infrared. http://dx.doi.org/10.1364/PRJ.4.000070 1. INTRODUCTION demonstrated by means of dynamic photopatterning tech- Eliminating polarization of incident light beams is critical, as it nique [14], which is suitable for the creation of high-quality may significantly affect the performance of optical appara- LC alignment in high resolution [15,16]. The LC depolarizer tuses. For example, grating-based spectrometers are sensitive is applicable for a wide wavelength range and monochromatic to the polarization of collected light [1], and the input polari- light in the telecom band.
    [Show full text]