OSM with KS Final Edits-1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

“Dizzy” Gillespie Was One of the Most Important and Influential Jazz Trumpeters, After Louis Armstrong
35 lesson9 Meet the Great Jazz Legends dizzygillespie Photo: © Carl Van Vechten, Library of Congress Vechten, Photo: © Carl Van IMPORTANT FACTS TO KNOW ABOUT JOHN “DIZZY” GILLESPIE Born: October 21, 1917, Cheraw, South Carolina Died: January 6, 1993, Englewood, New Jersey Period/Style of Jazz: Bebop, Afro-Cuban Jazz Instrument: Trumpet, bandleader and composer Major Compositions: A Night in Tunisia, Con Alma, Groovin’ High, Manteca Interesting Facts: Dizzy Gillespie invented the modern approach to jazz trumpet playing, which included extending the range of the instrument, improvising in a more linear fashion and playing with dramatic bursts with large interval leaps. He was among the first to use Afro-Cuban music in jazz. Included Listening: A Night in Tunisia Track 9 36 Meet the Great Jazz Legends ■ The Story of Dizzy Gillespie (1917–1993) ohn Birks “Dizzy” Gillespie was one of the most important and influential jazz trumpeters, after Louis Armstrong. Dizzy Gillespie, along with his colleagues Charlie Parker and Thelonious J Monk, are considered to be the “fathers” of the fast-and-furious style called bebop. Dizzy Gillespie was known for his soaring trumpet lines, his puffed cheeks and the tilted bell of his trumpet. He was loved by musicians and fans for his engaging personality and showmanship. Gillespie was inspired to play music by his father who was a bricklayer and part- time musician. Gillespie began playing the piano at the age of 4. He taught himself to play the trumpet by trial and error, with the help of a few friends at the age of 12. In 1935, Gillespie moved to Philadelphia with his mother, after the death of his father. -

Charles Mcpherson Leader Entry by Michael Fitzgerald
Charles McPherson Leader Entry by Michael Fitzgerald Generated on Sun, Oct 02, 2011 Date: November 20, 1964 Location: Van Gelder Studio, Englewood Cliffs, NJ Label: Prestige Charles McPherson (ldr), Charles McPherson (as), Carmell Jones (t), Barry Harris (p), Nelson Boyd (b), Albert 'Tootie' Heath (d) a. a-01 Hot House - 7:43 (Tadd Dameron) Prestige LP 12": PR 7359 — Bebop Revisited! b. a-02 Nostalgia - 5:24 (Theodore 'Fats' Navarro) Prestige LP 12": PR 7359 — Bebop Revisited! c. a-03 Passport [tune Y] - 6:55 (Charlie Parker) Prestige LP 12": PR 7359 — Bebop Revisited! d. b-01 Wail - 6:04 (Bud Powell) Prestige LP 12": PR 7359 — Bebop Revisited! e. b-02 Embraceable You - 7:39 (George Gershwin, Ira Gershwin) Prestige LP 12": PR 7359 — Bebop Revisited! f. b-03 Si Si - 5:50 (Charlie Parker) Prestige LP 12": PR 7359 — Bebop Revisited! g. If I Loved You - 6:17 (Richard Rodgers, Oscar Hammerstein II) All titles on: Original Jazz Classics CD: OJCCD 710-2 — Bebop Revisited! (1992) Carmell Jones (t) on a-d, f-g. Passport listed as "Variations On A Blues By Bird". This is the rarer of the two Parker compositions titled "Passport". Date: August 6, 1965 Location: Van Gelder Studio, Englewood Cliffs, NJ Label: Prestige Charles McPherson (ldr), Charles McPherson (as), Clifford Jordan (ts), Barry Harris (p), George Tucker (b), Alan Dawson (d) a. a-01 Eronel - 7:03 (Thelonious Monk, Sadik Hakim, Sahib Shihab) b. a-02 In A Sentimental Mood - 7:57 (Duke Ellington, Manny Kurtz, Irving Mills) c. a-03 Chasin' The Bird - 7:08 (Charlie Parker) d. -

New Jazz Label Discography
New Jazz Label Discography 10 Inch 100 Series: NJ 101 - Lennie Tristano and Lee Konitz - Lennie Tristano and Lee Konitz [1950] This album was reissued as Prestige 101. Side One Lee Konitz Marshmallow/Sound-Lee/Fishin’ Around/Tautology//Side Two Lennie Tristano Subconscious-Lee/Judy/Retrospection/Progression 10 Inch 1100 Series: NJLP 1101 - Jimmy Raney Quartet - Jimmy Raney Quartet [1954] Reissued as Prestige 201. Double Image/On the Square/Minor/Some Other Spring NJLP 1102 - Zoot Sims Quintet - Zoot Sims Quintet [1954] Reissued as Prestige 202. Howdy Podner/Toot, No. 2/Indian Summer/What's New? NJLP 1103 - Jimmy Raney Quintet - Jimmy Raney Quintet [1954] Reissued as Prestige 203. Stella by Starlight/Jo- Anne/Back and Blow/Five NJLP 1104 - Phil Woods Quintet - Phil Woods Quintet [1954] Reissued as Prestige 204. Pot Pie/Open Door/Robin's Bobbin'/Mad About the Girl NJLP 1105 - Jon Eardley Quartet - Jon Eardley Quartet [1955] Reissued as Prestige 205. Lute Leader/Indian Spring/Black/Cross NJLP 1106 - Teddy Charles Quartet - Teddy Charles Quartet [1955] Reissued as Prestige 206. Violetta/Relaxo Abstracto/Speak Low/Jay Walkin'/The Night We Called It a Day/I Can't Get Started 12 Inch 8200 Series: NJLP 8201 - Mal 3/Sounds - Mal Waldron [1/58] Tensions/Ollie's Caravan/The Cattin' Toddler/Portrait of a Young Mother/For Every Man There's a Woman NJLP 8202 - Roots – Prestige All Stars [1959] Roots/Sometimes I Feel Like a Motherless Child/Down by the Riverside NJLP 8203 - Farmer's Market - Art Farmer [1959] Reminiscing/By Myself/Wailing with Hank/With -

Dizzy Gillespie and the Big Band: GILLESPIANA (Verve V6-8394)
JAMU 20150422-2 –Dizzy Gillespie-Lalo Schifrin suites (ukázky) Dizzy Gillespie and His Orchestra: A PORTRAIT OF DUKE ELLINGTON (Verve V6-8386) A1 In A Mellow Tone 3:44 A2 Things Ain't What They Used To Be 4:50 A3 Serenade To Sweden 4:23 A4 Chelsea Bridge 2:34 A5 Upper Manhatten Medical Group 3:05 A6 Do Nothin' Till You Hear From Me 2:38 B1 Caravan 5:18 B2 Sophisticated Lady 3:19 B3 Johnny Come Lately 3:35 B4 Perdido 4:47 B5 Come Sunday 2:56 Trumpet – Dizzy Gillespie Trombone – Bennie Green French Horn – Joe Singer, Ray Alonge, Richard Berg Tuba – Jay McAllister Flute – Robert DiDomenica Woodwind – Ernest Bright, John Murtaugh, Paul Richie, Stan Webb Vibraphone – George Devens Piano, Celeste – Hank Jones Bass – George Duvivier Drums – Charlie Persip Arranged By – Clare Fisher Recorded on 27-28 April, 1960 in NYC. Dizzy Gillespie and the Big Band: GILLESPIANA (Verve V6-8394) A1 Prelude 5:52 A2 Blues 11:16 A3 Panamericana 4:39 B1 Africana 7:31 B2 Toccata 12:01 Trumpet – Clark Terry, Dizzy Gillespie, Ernie Royal, Joe Wilder, John Frosk Trombone – Britt Woodman, Frank Rehak, Paul Faulise, Urbie Green Horns – Al Richman, Gunther Schuller, James Buffington, Julius Watkins, Morris Secon, William Lister Tuba – Don Butterfield Saxophone – Leo Wright Piano, Written-By, Arranged By – Lalo Schifrin Bass – Art Davis Drums – Chuck Lampkin Bongos – Jack Del Rio Congas – Candido Timbales, Timpani – Willie Rodriguez Recorded November 14-15, 1960 in New York Dizzy Gillespie and the Big Band: CARNEGIE HALL CONCERT (Verve V6-8423) A1 Manteca 6:22 A2 This Is -

Grant Kicks Off FSU's Project of Building Sustainable Energy
For and about FSU people A publication of the FSU Division of Communications and Media Relations Volume 49, Number 28, April 29, 2019 Copy deadline: noon Wednesday, Candis Johnson at [email protected] Student Research Showcased in Undergraduate Symposium at FSU Student research and experiential learning projects will be the focus of FSU’s annual Undergraduate Research Symposium on Friday, May 3, from 11 a.m. to 2 p.m. in the Lane University Center. The symposium provides participants the opportunity to present their work to their peers and share experiences across disciplines. All three academic colleges will be represented for the first time this year. The event is free and open to members of the public, who may come at any time during the three-hour window. The symposium will feature the work of 248 students who were mentored by 52 members of the faculty or staff across all three colleges and 15 departments. The poster presentations, oral presentations and physical displays will represent work completed during 2018 and 2019. Some of the wide variety of topics to be covered will include a skills assessment of regional workforce among employers and employees, a conservative treatment of a rare type II odontoid fracture, inventories of amphibians and reptiles, a presentation on ignorance in interracial relationships, community colleges vs. universities, drone construction and remote sensing applications, the history of Deep Creek Lake, revealing the geometry of spiral galaxies using fourier transforms and much more. Students will be stationed at their research displays in Lane Manicur Hall to explain their findings to interested individuals. -
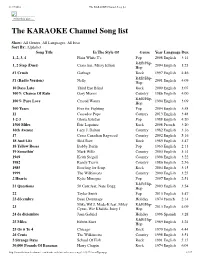
The KARAOKE Channel Song List
11/17/2016 The KARAOKE Channel Song list Print this List ... The KARAOKE Channel Song list Show: All Genres, All Languages, All Eras Sort By: Alphabet Song Title In The Style Of Genre Year Language Dur. 1, 2, 3, 4 Plain White T's Pop 2008 English 3:14 R&B/Hip- 1, 2 Step (Duet) Ciara feat. Missy Elliott 2004 English 3:23 Hop #1 Crush Garbage Rock 1997 English 4:46 R&B/Hip- #1 (Radio Version) Nelly 2001 English 4:09 Hop 10 Days Late Third Eye Blind Rock 2000 English 3:07 100% Chance Of Rain Gary Morris Country 1986 English 4:00 R&B/Hip- 100% Pure Love Crystal Waters 1994 English 3:09 Hop 100 Years Five for Fighting Pop 2004 English 3:58 11 Cassadee Pope Country 2013 English 3:48 1-2-3 Gloria Estefan Pop 1988 English 4:20 1500 Miles Éric Lapointe Rock 2008 French 3:20 16th Avenue Lacy J. Dalton Country 1982 English 3:16 17 Cross Canadian Ragweed Country 2002 English 5:16 18 And Life Skid Row Rock 1989 English 3:47 18 Yellow Roses Bobby Darin Pop 1963 English 2:13 19 Somethin' Mark Wills Country 2003 English 3:14 1969 Keith Stegall Country 1996 English 3:22 1982 Randy Travis Country 1986 English 2:56 1985 Bowling for Soup Rock 2004 English 3:15 1999 The Wilkinsons Country 2000 English 3:25 2 Hearts Kylie Minogue Pop 2007 English 2:51 R&B/Hip- 21 Questions 50 Cent feat. Nate Dogg 2003 English 3:54 Hop 22 Taylor Swift Pop 2013 English 3:47 23 décembre Beau Dommage Holiday 1974 French 2:14 Mike WiLL Made-It feat. -

Jazz Studies Handbook 2021-2022
BOB COLE CONSERVATORY OF MUSIC California State University, Long Beach JAZZ STUDIES HANDBOOK 2021-2022 1 TABLE OF CONTENTS Welcome to “Jazz at the Beach” 4 The Jazz Studies Faculty 5 Applied Lessons 8 Performance Ensembles 10 Scholarships & Financial Aid 13 Incoming Student Audition Requirements 14 Ensemble Placement Auditions 15 Ensemble Requirements and Protocol 18 B.M. in Jazz Studies Curriculum 21 M.M. in Jazz Studies Curriculum 21 Jazz Course Descriptors 22 Jury Requirements 25 Instrumental Jazz Juries 26 Instrumental Tune Lists 28 Vocal Jazz Juries 30 Recital Guidelines 32 Instrumental Jazz Recital Content 34 2 Vocal Jazz Recital Content 35 Recital Approval 36 Sample Recital Approval Worksheet 37 Planning Your Coursework 38 Building Your Professional Network 40 Performance Policies 41 Concert and Jazz Forum Attendance 43 Miscellaneous Performances 45 Tour Policies 46 Jazz Area Meetings 48 Contact Information 49 3 WELCOME TO “JAZZ AT THE BEACH” In 1975, California State University, Long Beach became the first university in California and one of fifteen in the nation to offer a degree in Jazz Studies. “Jazz at the Beach” has become one of the most respected collegiate jazz studies programs in the United States. College Factual magazine listed CSULB as the “#1 Best Value For The Money” in California and in the top 15% for nation. Our campus is situated less than three miles from the Pacific Ocean in one of the most desirable microclimates in Southern California. Long Beach is California’s 7th largest city, yet it has a small town feel. Our proximity to the world’s largest entertainment center allows our students to start building their professional networks while still in school. -

June 2021 ITG Journal
International Trumpet Guild® Journal to promote communications among trumpet players around the world and to improve the artistic level of performance, teaching, and literature associated with the trumpet June 2021 ITG Journal The International Trumpet Guild® (ITG) is the copyright owner of all data contained in this file. ITG gives the individual end-user the right to: • Download and retain an electronic copy of this file on electronic devices for the sole use of the end-user • Print a single copy of this file • Quote fair-use passages of this file in not-for-profit research papers as long as the ITG Journal, date, and page number are cited as the source. The International Trumpet Guild®, under the umbrella of United States and international copyright laws, prohibits the following without prior writ ten permission from the Publications Editor of the ITG: • Duplication or distribution of this file or its contents in any manner that does not conform with the uses as stated above • Alteration of this file or the data contained herein • Placement of this file on any web site, server, or any other database or device that allows for the accessing or copying of this file or the data contained herein by any party, including such a device intended to be used wholly within an institution. By scrolling past this page you agree to the fair use guidelines stated above. http://www.trumpetguild.org This cover sheet must accompany this file. The removal of this information is strictly prohibited and can result in expulsion from the organization and legal action. -

The Jazz/Latin Jam" Stars Deserving Wider Recognition
-tionwith • -· • ter tsner .-.. u ..........~ln -- itorium • _eat s........ t '--ton-~·-~~ - liK:kets: $5.00 St s: .00 S""""' ~ -+- Balcony: 2.50 Ttekets at office or mail..._~ ke c ks payable to: University J York University • Jon Faddt •~ trumQt t. Andrea Brach· ,..,... feld I Joe Farrell. flute, tenor IIJCOPhone, Ray lryant. plano, Joe Beck. guitar. Herb Buehler. IN baal. Jimmy Madiaon. Mel Lewla, drums, Ray Bar .. with IIYU board Ntto. congaa, Terl Thornton. vocals Leaderle Jam e aon aenerally nrc DAY OCTOBER 7, 8:00 PM p ~ ' or o y crha~ s. But Ja k Klein Inger. little more than a year ao, begun hi " lligh· haht In Jazz" on the premi e thnt whatever Jon Faddis Joe Farrelf the circum tance , good musicmns will pro Qucwtet with Herb BUshier Jimmy Madison duce aood nnwic. He handph;; ks th e: trtl ent , Tldceta at box office or by mail order MOire checks payable to: emcee the shows, and even . ugge l orne of New Yoet Unlverlity the proaramming- though the rti t hold • Tldets: 15.00 Students: ~ . 00 Student Balcony: $2.50 • full control. Sc'lmetime it come out tilted NYU Loeb ...,.... Center Rlaner end Lubin Audltortum nd pat ~ more often we hark b ck to Norm u1 -La ...... "•c• 11 Sq. South ~~~~: !5H!!i~!!7!57~------_J Granz" epochal groupings. fhi wus one of tho e moment . The opening Walk in ' et the evening's pace: II joined in to take a few wurm-up choru.~ e I But at wa n't until the stage cleared, leaving Bryant alone, that the virtuo ity began in car ne t. -
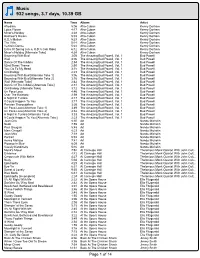
Jazz Library (Song Listings)
Music 932 songs, 3.7 days, 10.39 GB Name Time Album Artist Afrodisia 5:06 Afro-Cuban Kenny Dorham Lotus Flower 4:17 Afro-Cuban Kenny Dorham Minor's Holiday 4:28 Afro-Cuban Kenny Dorham Basheer's Dream 5:03 Afro-Cuban Kenny Dorham K.D.'s Motion 5:29 Afro-Cuban Kenny Dorham The Villa 5:24 Afro-Cuban Kenny Dorham Venita's Dance 5:22 Afro-Cuban Kenny Dorham Echo Of Spring (a.k.a. K.D.'s Cab Ride) 6:12 Afro-Cuban Kenny Dorham Minor's Holiday [Alternate Take] 4:24 Afro-Cuban Kenny Dorham Bouncing With Bud 3:05 The Amazing Bud Powell, Vol. 1 Bud Powell Wail 3:06 The Amazing Bud Powell, Vol. 1 Bud Powell Dance Of The Infidels 2:54 The Amazing Bud Powell, Vol. 1 Bud Powell 52nd Street Theme 2:50 The Amazing Bud Powell, Vol. 1 Bud Powell You Go To My Head 3:15 The Amazing Bud Powell, Vol. 1 Bud Powell Ornithology 2:23 The Amazing Bud Powell, Vol. 1 Bud Powell Bouncing With Bud [Alternate Take 1] 3:06 The Amazing Bud Powell, Vol. 1 Bud Powell Bouncing With Bud [Alternate Take 2] 3:16 The Amazing Bud Powell, Vol. 1 Bud Powell Wail [Alternate Take] 2:42 The Amazing Bud Powell, Vol. 1 Bud Powell Dance Of The Infidels [Alternate Take] 2:51 The Amazing Bud Powell, Vol. 1 Bud Powell Ornithology [Alternate Take] 3:12 The Amazing Bud Powell, Vol. 1 Bud Powell Un Poco Loco 4:46 The Amazing Bud Powell, Vol. -

Norgran Label Discography
Norgran Label Discography Norgran Label 10 Inch Series MGN 1 - Swing - Johnny Hodges [11/54] Reissue of Clef MG-C-151. Wham/Latino/Through For the Night/Sheik of Araby//Hodgepodge/Jappa/My Reward/Something To Pat Your Foot To MGN 2 - Dizzy Gillespie & Stan Getz Sextet - Dizzy Gillespie & Stan Getz Sextet [195?] It Don’t Mean a Thing/It’s the Talk of the Town/Exactly Like You/I Let a Song Go Out of My Heart MGN 3 - Buddy DeFranco Quartet - Buddy DeFranco Quartet [2/54] Reissue of Clef MG-C-149. But Not For Me/When Your Lover Has Gone/Ferdinando/The Things We Did Last Summer MGN 4 – Al Hibbler Favorites - Al Hibbler [195?] Please/Believe It, Beloved/There is No Greater Love/It Must Be True/As Time Goes By/Anne/You and I/I’m Getting Sentimental Over You MGN 5 – Lester Young with the Oscar Peterson Trio Number 1 - Lester Young & Oscar Peterson Trio [195?] Ad Lib Blues/Just You, Just Me/I Can’t Get Started/Almost Like Being in Love MGN 6 - Lester Young with the Oscar Peterson Trio Number 2 - Lester Young & Oscar Peterson Trio [195?] Tea for Two/Indiana/On the Sunny Side of the Street/There’ll Never Be Another You MGN 7 - Amazing Artistry of Louis Bellson - Louis Bellson [195?] Fascinatin’ Rhythm/Copasetic/Percussionistally Speaking/All God’s Chillun Got Rhythm/A Peart for Louie MGN 8 - Charlie Ventura Quartet - Charlie Ventura Quartet [195?] Ain’t Misbehavin’/Blue Prelude/Girl of My Dreams/Limehouse Blues/Blues for Two/Somebody Loves Me/Crazy Rhythm/All the Things You Are MGN 9 - Second Afro-Cuban Jazz Suite - Chico O’Farrill [6/54] The Second -

Page | 1 Funding for the Smithsonian Jazz Oral History Program NEA
Funding for the Smithsonian Jazz Oral History Program NEA Jazz Master interview was provided by the National Endowment for the Arts. JACKIE MCLEAN NEA Jazz Master (2001) Interviewee: Jackie McLean (May 17, 1931 – March 31, 2006) Interviewer: William Brower with recording engineer Sven Abow Date: July 20-21, 2001 Repository: Archives Center, National Museum of American History. Smithsonian Institution Description: Transcript, 131 pp. Brower: My name is William Brower. I’m sitting with Jackie McLean at the Artists Collective in Hartford, Connecticut, on Friday, July the 20th, 2001. We’re conducting an oral history interview for the Smithsonian Jazz Oral History Project. The first thing I’d like to do is thank Mr. McLean for agreeing to participate in this oral history. McLean: Oh, it’s my pleasure. It’s very important. Brower: I want to start with what we were talking about before we actually started the formal interview and ask you to tell us about your recent trip to Europe, where you played, with whom you were playing, and then talk about how you’re handling your performance – the performance dimension of your life – right now. McLean: This most recent trip that I made – I made two trips to play with Mal Waldron. The first one was in Verona, Italy, a couple of weeks ago. That was a duo where Mal and I played for about 70 minutes solo, between he and I, duo. Then I went just last week over to the North Sea Festival in the Hague to play with Mal again, this time with his trio, with Andrew Cyrille, Reggie Workman, Mal, and I was special guest.