An Answer to the Conjecture of Satnoianu∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

List of Participants Page 1
Chanchun Summer Institute List of Participants July 2011 Has given a course (C) / SURNAME GIVEN NAME AFFILIATION In Chinese talk (T) BAI Zhidong Northesat Normal Univ., Changchun 白志东 C BAO Zhi-Gang Zhejiang University 鲍志刚 BIANE Philippe CNRS and Université Paris-Est C BORDENAVE Charles CNRS and Université Paul Sabatier C CHAFAÏ Djalil Université Paris-Est C CHEBALLAH Hayat Université Paris-Nord CHEN Jiaqi Northeast Normal University 陈佳奇 DING Yitao Northwest University 丁毅涛 DONATI-MARTIN Catherine Université Pierre et Marie Curie C FEVRIER Maxime Université Paul Sabatier GAO Wei Northeast Normal University 高巍 GENG Weiqiang Henan Normal University 耿卫强 GUIONNET Alice CNRS, Ecole Normale de Lyon C GUO Jianhua Northeast Normal University 郭建华 HARDY Adrien Université Paul Sabatier T HE Shu-Yuan Capital Normal University 何书元 HU Junying Northwest University 胡俊英 HU Jiang Northeast Normal University 胡江 HUI Yongchang Northeast Normal University 惠永昌 JIANG Tiefeng University of Minnesota 蒋铁锋 C JIANG Dandan Jilin University 蒋丹丹 T KHAROUF Malika Télécom ParisTech T LI Weiming Beihang Uiniversity 李卫明 LI Nan Henan Normal University 李楠 LI Wenbo University of Delware 李文波 T LI Xiang-Dong Chinese Academy of Sciences 李向东 C LI Zhen Northwest University 李振 LIU Guo-Ping Chinese Academy of Sciences 刘国平 Liu Yuan Chinese Academy of Sciences 刘源 LU Dawei Dalian University of Technology 鲁大伟 MAIDA Mylène Université Paris-Sud T MALE Camille Ecole Normale de Lyon T MAUREL-SEGALA Edouard Université Paris-Sud MIAO Baiqi University of Sciences and Technology of China 缪百其 T -

The Spreading of Christianity and the Introduction of Modern Architecture in Shannxi, China (1840-1949)
Escuela Técnica Superior de Arquitectura de Madrid Programa de doctorado en Concervación y Restauración del Patrimonio Architectónico The Spreading of Christianity and the introduction of Modern Architecture in Shannxi, China (1840-1949) Christian churches and traditional Chinese architecture Author: Shan HUANG (Architect) Director: Antonio LOPERA (Doctor, Arquitecto) 2014 Tribunal nombrado por el Magfco. y Excmo. Sr. Rector de la Universidad Politécnica de Madrid, el día de de 20 . Presidente: Vocal: Vocal: Vocal: Secretario: Suplente: Suplente: Realizado el acto de defensa y lectura de la Tesis el día de de 20 en la Escuela Técnica Superior de Arquitectura de Madrid. Calificación:………………………………. El PRESIDENTE LOS VOCALES EL SECRETARIO Index Index Abstract Resumen Introduction General Background........................................................................................... 1 A) Definition of the Concepts ................................................................ 3 B) Research Background........................................................................ 4 C) Significance and Objects of the Study .......................................... 6 D) Research Methodology ...................................................................... 8 CHAPTER 1 Introduction to Chinese traditional architecture 1.1 The concept of traditional Chinese architecture ......................... 13 1.2 Main characteristics of the traditional Chinese architecture .... 14 1.2.1 Wood was used as the main construction materials ........ 14 1.2.2 -

Editors-In-Chief: Ma, Hongbao, Ph.D
, '" Life Science Journal Acta Zhengzhou University Overseas Edition Life Science Journal, the Acta Zhengzhou University Overseas Edition, is an international journal with the purpose to enhance our natural and scientific knowledge dissemination in the world under the free publication princi- ple. The journal is calling for papers from all who are associated with Zhengzhou University - home and abroad. Any valuable papers or reports that are related to life science are welcome. Other academic articles that are less rele- vant but are of high quality will also be considered and published. Papers submitted could be reviews, objective de- scriptions, research reports, opinions/debates, news, letters, and other types of writings. All publications of Life Science ]aurnal are under vigorous peer-review. Let's work together to disseminate our research results and our opmlons. Editorial Board: Editor- in-Chief: Shen,Changyu, Ph. D. , Zhengzhou University, China Associate Editors-in-Chief: Ma, Hongbao, Ph.D. , Michigan State University, USA Xin, Shijun, Prof. , Zhengzhou University, China Li, Qingshan, Ph.D., Zhengzhou University, China Cherng, Shen, Ph. D. , M. D. , Chengshiu University, China Editors: (in alphabetical order) An, Xiuli, Ph.D., New York Blood Center, USA Chen, George, Ph. D. , Michigan State University, USA Dong, Ziming, M. D. , Zhengzhou University, China Duan, Guangcai, Ph. D. , M. D. , Zhengzhou University, China Edmondson, Jingiing Z. , Ph. D. , Zhejiang University, China Li, Xinhua, M. D. , Zhengzhou University, China Li, Yuhua, Ph. D. , Emory University, USA Lindley, Mark, Ph. D. , Columbia University, USA Liu, Hongmin, Ph. D. , Zhengzhou University, China Liu, Zhanju, Ph. D. , M. D. , Zhengzhou University, China Lu, Longdou, Ph. -

University of Leeds Chinese Accepted Institution List 2021
University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams. -
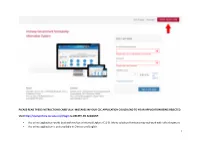
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • CLIC on the Edit Personal Details button. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. o Once you have completed this section click Verify and Save. 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. o Once you have completed this section, click Verify and Save. 5 • Provide the contact information of the host Chinese university. o The contact information for summer programs is available on the CLIC website in the Program Finder. o For exchange programs, please contact your home university international office to get your host university contact information (http://clicstudyinchina.com/contact-us/). -
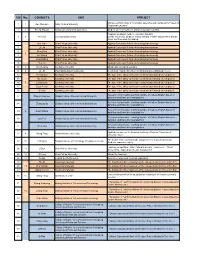
S/N No. CONTACTS UNIT PROJECT
S/N No. CONTACTS UNIT PROJECT Mobile teaching mode of "Computer assembly and maintenance" based on 1 1 Sun Wenjuan Anhui Xinhua University "Superstar Emulator" 2 2 Zheng Zhiyuan China University of Geosciences Student oriented multilevel and stereoscopic teaching Propping on Bloom model + education big data 3 3 He Xinyi Chongqing University private enjoyment, pleasure enjoyment and creative enjoyment of design class, the three-step flip landing. 4 Hou Yani Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 5 Liu Jia Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 6 Meng Jiao Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 4 7 Hu Xiaojia Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 8 Long Kaihua Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 9 Yun Jie Xi'an Peihua University Applied Curriculum Reform of nursing pharmacology 10 5 Wu Wenjing Xuchang University Situational simulation teaching 11 6 Liu Jin Guangdong Baiyun University Curriculum construction of accounting principles (Bilingual) course 12 Yu Xianxian Xuchang University The type of the ability curriculum constructionon based on real project 13 Wu Guoxi Xuchang University The type of the ability curriculum constructionon based on real project 14 7 Li Manyuan Xuchang University The type of the ability curriculum constructionon based on real project 15 Zhao Putian Xuchang University The type of the ability curriculum constructionon based on real project -

The Status Quo and Reform Thinking of the Talent Training Mode of Biology Teachers in Middle School
Journal of Education and Learning; Vol. 9, No. 6; 2020 ISSN 1927-5250 E-ISSN 1927-5269 Published by Canadian Center of Science and Education The Status Quo and Reform Thinking of the Talent Training Mode of Biology Teachers in Middle School Bo Peng1, Chuanling Zhang1, Feng Peng2, Xuezhong Sun3, Xiayu Tian1, Xiaorui Ma1, Ruihua Pang1, Yanfang Sun1, Wei Zhou1 & Quanxiu Wang1 1 College of Life Sciences, Xinyang Normal University, Xinyang, Henan, China 2 Biology Teaching Group, Gushi No. 1 Middle School, Gushi County, Henan, China 3 Henan XinYang Senior High School, Xinyang, Xinyang, Henan, China Correspondence: Bo Peng, College of Life Sciences, Xinyang Normal University, Xinyang, Henan 464000, China. E-mail: [email protected] Received: September 13, 2020 Accepted: November 3, 2020 Online Published: November 12, 2020 doi:10.5539/jel.v9n6p84 URL: https://doi.org/10.5539/jel.v9n6p84 Abstract It has always been one of the hot spots of the whole society to improve teachers’ quality and ability. With the progress of the era and the rapid development of biology, it puts forward higher requirements for the cultivation of biology teachers of middle school. How to cultivate a large number of high-quality biology teachers of middle school with good ethics and outstanding abilities is a focus problem worth exploring. There are some problems in the traditional training mode of biology normal students, such as backward teaching idea, unreasonable teaching arrangement and uneven teaching level. In view of these problems, normal universities should take a series of reform measures to promote the professional development of middle school biology teachers. -

EVJR1407 Ex-Post I-1 Henan
People’s Republic of China Ex-Post Evaluation of Japanese ODA Loan Project “Inland Higher Education Project (Regional Vitalization, Market Economy Reform Support, and Environmental Conservation) (Henan Province)” External Evaluator: Takako Haraguchi, OPMAC Corporation 0. Summary This project aimed to improve teaching and research at eleven major universities in Henan Province through the development of their facilities and equipment as well as providing training for teachers. Relevance of the project was evaluated to be high, as it was in line with (i) the higher education policies of China and Henan Province, (ii) development needs for quantitative and qualitative enhancement of the universities, and (iii) Japan’s assistance policies. Effectiveness/impact was also high, based on the observations that the project satisfied such needs, improved education activities by enabling more experiments, and improved research activities through outcomes achieved from advanced equipment and training, and thereby contributed to the promotion of the key industries as well as environmental conservation. Efficiency of the project was evaluated to be fair on the whole: although the project cost was within the plan, the project period significantly exceeded the planned period due to factors such as delays in the building construction following changes in location. Sustainability was evaluated to be high, with no problem observed in institutional, technical and financial aspects, and due to the good status of operation and maintenance of the facilities and equipment developed by the project. In light of the above, this project is evaluated to be highly satisfactory. 1. Project Description Project Location Social Science Building of Zhengzhou University 1 1.1 Background1 In China, together with the remarkable economic development, several development issues have arisen such as narrowing internal disparity between coastal and inland areas, reducing poverty, preparing for joining in the World Trade Organization (WTO) and handling global issues. -

Crystal Structure of 2-Bromo- 1,3,6,8-Tetramethylbophy (BOPHY
Z. Kristallogr. - N. Cryst. Struct. 2021; 236(5): 949–952 Weifeng He, Yingfan Liu*, Saisai Sun, Guangqian Ji and Xiaochuan Li* Crystal structure of 2-bromo- 1,3,6,8-tetramethylBOPHY (BOPHY = bis(difluoroboron)-1,2-bis((1H-pyrrol-2-yl) methylene)hydrazine), C14H15B2BrF4N4 https://doi.org/10.1515/ncrs-2021-0163 Received April 26, 2021; accepted May 17, 2021; published online June 21, 2021 Abstract C14H15B2BrF4N4, orthorhombic, Pbca (no. 61), a = 11.970(1) Å, b = 10.049(1) Å, c = 27.847(1) Å, V = 3349.6 Å3, 2 Z =8,Rgt(F) = 0.0697, wRref(F ) = 0.1585, T = 296 K. CCDC no.: 2080820 The molecular structure is shown in Figure 1. Table 1 con- tains crystallographic data and Table 2 contains the list of the atoms including atomic coordinates and displacement parameters. Source of material 2-Bromo-1,3,6,8-tetramethylBOPHY was synthesized accord- ing to the literature [6–9]. Firstly, 2,4-dimethylpyrrole and boron trifluoride etherate were condensed at room tempera- ture to give 1,3,6,8-tetram-ethylBOPHY [6, 7]. Next, bromi- nation of 1,3,6,8-tetramethyl-BOPHY would give single or double bromine substituted BOPHY derivatives by treating it with a halogenation reagent. Copper(II) bromide and N- bromosuccinimide (NBS) are all candidates for bromination of 1,3,6,8-tetramethylBOPHY. However, bromination with NBS is an economic selection, together with the advantage *Corresponding authors: Yingfan Liu, College of Material and Chemical Engineering, Zhengzhou University of Light Industry, Henan Provincial Key Lab of Surface and Interface Science, Zhengzhou 450002, P. -
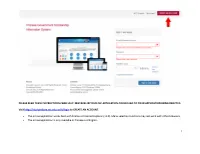
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. -
CONICYT Ranking Por Disciplina > Sub-Área OECD (Académicas) Comisión Nacional De Investigación 1
CONICYT Ranking por Disciplina > Sub-área OECD (Académicas) Comisión Nacional de Investigación 1. Ciencias Naturales > 1.3 Ciencias Físicas y Astronomía Científica y Tecnológica PAÍS INSTITUCIÓN RANKING PUNTAJE FRANCE Universite Paris Saclay (ComUE) 1 5,000 USA University of California Berkeley 2 5,000 USA California Institute of Technology 3 5,000 USA Massachusetts Institute of Technology (MIT) 4 5,000 USA Harvard University 5 5,000 USA Stanford University 6 5,000 UNITED KINGDOM University of Cambridge 7 5,000 FRANCE Sorbonne Universite 8 5,000 USA University of Chicago 9 5,000 JAPAN University of Tokyo 10 5,000 UNITED KINGDOM University of Oxford 11 5,000 FRANCE Universite Sorbonne Paris Cite-USPC (ComUE) 12 5,000 FRANCE University of Paris Diderot 13 5,000 FRANCE PSL Research University Paris (ComUE) 14 5,000 USA Princeton University 15 5,000 FRANCE Universite Paris Sud - Paris XI 16 5,000 CHINA Tsinghua University 17 5,000 USA University of Maryland College Park 18 5,000 UNITED KINGDOM University College London 19 5,000 UNITED KINGDOM Imperial College London 20 5,000 FRANCE Communaute Universite Grenoble Alpes 21 5,000 USA University of Michigan 22 5,000 CANADA University of Toronto 23 5,000 FRANCE Universite Grenoble Alpes (UGA) 24 5,000 ITALY Sapienza University Rome 25 5,000 ITALY University of Padua 26 5,000 CHINA Peking University 27 5,000 UNITED KINGDOM University of Edinburgh 28 5,000 USA University of Illinois Urbana-Champaign 29 5,000 USA Columbia University 30 5,000 INDIA Indian Institute of Technology System (IIT System) -
THE TANCI FICTION JING ZHONG ZHUAN by YU ZHANG A
THE FEMALE REWRITING OF GRAND HISTORY: THE TANCI FICTION JING ZHONG ZHUAN by YU ZHANG A DISSERTATION Presented to the Department of East Asian Languages and Literatures and the Graduate School of the University of Oregon in partial fulfillment of the requirements for the degree of Doctor of Philosophy June 2013 DISSERTATION APPROVAL PAGE Student: Yu Zhang Title: The Female Rewriting of Grand History: The Tanci Fiction Jing zhong zhuan This dissertation has been accepted and approved in partial fulfillment of the requirements for the Doctor of Philosophy degree in the Department of East Asian Languages and Literatures by: Maram Epstein Chairperson Tze-lan Sang Core Member Yugen Wang Core Member Bryna Goodman Institutional Representative and Kimberly Andrews Espy Vice President for Research and Innovation; Dean of the Graduate School Original approval signatures are on file with the University of Oregon Graduate School. Degree awarded June 2013 ii © 2013 Yu Zhang iii DISSERTATION ABSTRACT Yu Zhang Doctor of Philosophy Department of East Asian Languages and Literatures June 2013 Title: The Female Rewriting of Grand History: The Tanci Fiction Jing zhong zhuan This dissertation has examined the tanci fiction Jing zhong zhuan, or A Biography of Dedication and Loyalty, authored by a gentry woman writer Zhou Yingfang in the late nineteenth century. I argue that by adapting the well-known patriotic story of General Yue Fei in Chinese history, Zhou Yingfang suggests new directions in grand historical narrative in her own voice and from her own perspective. Negotiating the writing conventions of earlier legends, she turns the stereotyped masculine image of Yue Fei into a hero in both public and domestic settings.