Proposal) RA PTIME X⊆ + ⊇ X⊇ X X
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tarjan Transcript Final with Timestamps
A.M. Turing Award Oral History Interview with Robert (Bob) Endre Tarjan by Roy Levin San Mateo, California July 12, 2017 Levin: My name is Roy Levin. Today is July 12th, 2017, and I’m in San Mateo, California at the home of Robert Tarjan, where I’ll be interviewing him for the ACM Turing Award Winners project. Good afternoon, Bob, and thanks for spending the time to talk to me today. Tarjan: You’re welcome. Levin: I’d like to start by talking about your early technical interests and where they came from. When do you first recall being interested in what we might call technical things? Tarjan: Well, the first thing I would say in that direction is my mom took me to the public library in Pomona, where I grew up, which opened up a huge world to me. I started reading science fiction books and stories. Originally, I wanted to be the first person on Mars, that was what I was thinking, and I got interested in astronomy, started reading a lot of science stuff. I got to junior high school and I had an amazing math teacher. His name was Mr. Wall. I had him two years, in the eighth and ninth grade. He was teaching the New Math to us before there was such a thing as “New Math.” He taught us Peano’s axioms and things like that. It was a wonderful thing for a kid like me who was really excited about science and mathematics and so on. The other thing that happened was I discovered Scientific American in the public library and started reading Martin Gardner’s columns on mathematical games and was completely fascinated. -

Qualitative and Quantitative Security Analyses for Zigbee Wireless Sensor Networks
Downloaded from orbit.dtu.dk on: Sep 27, 2018 Qualitative and Quantitative Security Analyses for ZigBee Wireless Sensor Networks Yuksel, Ender; Nielson, Hanne Riis; Nielson, Flemming Publication date: 2011 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Yuksel, E., Nielson, H. R., & Nielson, F. (2011). Qualitative and Quantitative Security Analyses for ZigBee Wireless Sensor Networks. Kgs. Lyngby, Denmark: Technical University of Denmark (DTU). (IMM-PHD-2011; No. 247). General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Qualitative and Quantitative Security Analyses for ZigBee Wireless Sensor Networks Ender Y¨uksel Kongens Lyngby 2011 IMM-PHD-2011-247 Technical University of Denmark Informatics and Mathematical Modelling Building 321, DK-2800 Kongens Lyngby, Denmark Phone +45 45253351, Fax +45 45882673 [email protected] www.imm.dtu.dk IMM-PHD: ISSN 0909-3192 Summary Wireless sensor networking is a challenging and emerging technology that will soon become an inevitable part of our modern society. -

Finding Rising Stars in Co-Author Networks Via Weighted Mutual Influence
Finding Rising Stars in Co-Author Networks via Weighted Mutual Influence Ali Daud a,b Naif Radi Aljohani a Rabeeh Ayaz Abbasi a,c a Faculty of Computing and a Faculty of Computing and c Department of Computer Science, Information Technology, King Information Technology, King Quaid-i-Azam University, Islamabad, Abdulaziz University, Jeddah, Saudi Abdulaziz University, Jeddah, Saudi Pakistan Arabia Arabia [email protected] [email protected] [email protected] b b d Zahid Rafique Tehmina Amjad Hussain Dawood b Department of Computer Science b Department of Computer Science d Faculty of Computing and and Software Engineering, and Software Engineering, Information Technology, University International Islamic University, International Islamic University, of Jeddah, Jeddah, Saudi Arabia Islamabad, Pakistan Islamabad, Pakistan [email protected] [email protected] [email protected] a Khaled H. Alyoubi a Faculty of Computing and Information Technology, King Abdulaziz University, Jeddah, Saudi Arabia [email protected] ABSTRACT KEYWORDS Finding rising stars is a challenging and interesting task which is Bibliographic databases; Citations; Author Order; Rising Stars; Mutual being investigated recently in co-author networks. Rising stars are Influence; Co-Author Networks authors who have a low research profile in the start of their career but may become experts in the future. This paper introduces a new method Weighted Mutual Influence Rank (WMIRank) for finding 1. INTRODUCTION rising stars. WMIRank exploits influence of co-authors’ citations, The rapid evolution of scientific research has created large order of appearance and publication venues. Comprehensive volumes of publications every year, and is expected to continue in experiments are performed to analyze the performance of near future [21]. -

Moshe Y. Vardi
MOSHE Y. VARDI Address Office Home Department of Computer Science 4515 Merrie Lane Rice University Bellaire, TX 77401 P.O.Box 1892 Houston, TX 77251-1892 Tel: (713) 348-5977 Tel: (713) 665-5900 Fax: (713) 348-5930 Fax: (713) 665-5900 E-mail: [email protected] URL: http://www.cs.rice.edu/∼vardi Research Interests Applications of logic to computer science: • database systems • complexity theory • multi-agent systems • specification and verification of hardware and software Education Sept. 1974 B.Sc. in Physics and Computer Science (Summa cum Laude), Bar-Ilan University, Ramat Gan, Israel May 1980 M.Sc. in Computer Science, The Feinberg Graduate School, The Weizmann Insti- tute of Science, Rehovoth, Israel Thesis: Axiomatization of Functional and Join Dependencies in the Relational Model. Advisors: Prof. C. Beeri (Hebrew University) Prof. P. Rabinowitz Sept 1981 Ph.D. in Computer Science, Hebrew University, Jerusalem, Israel Thesis: The Implication Problem for Data Dependencies in the Relational Model. Advisor: Prof. C. Beeri Professional Experience Nov. 1972 – June 1973 Teaching Assistant, Dept. of Mathematics, Bar-Ilan University. Course: Introduction to computing. 1 Nov. 1978 – June 1979 Programmer, The Weizmann Institute of Science. Assignments: implementing a discrete-event simulation package and writing input-output routines for a database management system. Feb. 1979 – Oct. 1980 Research Assistant, Inst. of Math. and Computer Science, The Hebrew University of Jerusalem. Research subject: Theory of data dependencies. Nov. 1980 – Aug. 1981 Instructor, Inst. of Math. and Computer Science, The Hebrew University of Jerusalem. Course: Advanced topics in database theory. Sep. 1981 – Aug. 1983 Postdoctoral Scholar, Dept. of Computer Science, Stanford Univer- sity. -

Michael Oser Rabin Automata, Logic and Randomness in Computation
Michael Oser Rabin Automata, Logic and Randomness in Computation Luca Aceto ICE-TCS, School of Computer Science, Reykjavik University Pearls of Computation, 6 November 2015 \One plus one equals zero. We have to get used to this fact of life." (Rabin in a course session dated 30/10/1997) Thanks to Pino Persiano for sharing some anecdotes with me. Luca Aceto The Work of Michael O. Rabin 1 / 16 Michael Rabin's accolades Selected awards and honours Turing Award (1976) Harvey Prize (1980) Israel Prize for Computer Science (1995) Paris Kanellakis Award (2003) Emet Prize for Computer Science (2004) Tel Aviv University Dan David Prize Michael O. Rabin (2010) Dijkstra Prize (2015) \1970 in computer science is not classical; it's sort of ancient. Classical is 1990." (Rabin in a course session dated 17/11/1998) Luca Aceto The Work of Michael O. Rabin 2 / 16 Michael Rabin's work: through the prize citations ACM Turing Award 1976 (joint with Dana Scott) For their joint paper \Finite Automata and Their Decision Problems," which introduced the idea of nondeterministic machines, which has proved to be an enormously valuable concept. ACM Paris Kanellakis Award 2003 (joint with Gary Miller, Robert Solovay, and Volker Strassen) For \their contributions to realizing the practical uses of cryptography and for demonstrating the power of algorithms that make random choices", through work which \led to two probabilistic primality tests, known as the Solovay-Strassen test and the Miller-Rabin test". ACM/EATCS Dijkstra Prize 2015 (joint with Michael Ben-Or) For papers that started the field of fault-tolerant randomized distributed algorithms. -

Datalog Unchained
Datalog Unchained Victor Vianu UC San Diego & Inria [email protected] ABSTRACT robust class of fixpoint queries, previously defined by extensions of This is the companion paper of a talk in the Gems of PODS se- first-order logic with a fixpoint operator. ries, that reviews the development, starting at PODS 1988, of a The two PODS 1988 articles initiated a line of research [3, 6, 8, family of Datalog-like languages with procedural, forward chain- 14, 15, 104, 116] that extended the forward chaining approach to an ing semantics, providing an alternative to the classical declarative, entire family of Datalog-like languages, providing an alternative model-theoretic semantics. These languages also provide a unified paradigm for database queries, with natural counterparts to classical formalism that can express important classes of queries including query languages including the fixpoint and while queries, and all the fixpoint, while, and all computable queries. They can also incor- way to computable queries. The forward chaining approach turned porate in a natural fashion updates and nondeterminism. Datalog out to also be suitable for studying nondeterministic languages, variants with forward chaining semantics have been adopted in a yielding an appealing unifying formalism. The present paper tells variety of settings, including active databases, production systems, the story of this development. distributed data exchange, and data-driven reactive systems. After a brief review of classical query languages, we turn to Datalog and its extensions. We begin with an informal overview of ACM Reference Format: Datalog and Datalog: with stratified and well-founded semantics. Victor Vianu. 2021. Datalog Unchained. -
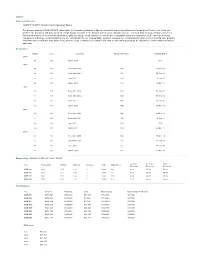
SIGACT Viability
SIGACT Name and Mission: SIGACT: SIGACT Algorithms & Computation Theory The primary mission of ACM SIGACT (Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory) is to foster and promote the discovery and dissemination of high quality research in the domain of theoretical computer science. The field of theoretical computer science is interpreted broadly so as to include algorithms, data structures, complexity theory, distributed computation, parallel computation, VLSI, machine learning, computational biology, computational geometry, information theory, cryptography, quantum computation, computational number theory and algebra, program semantics and verification, automata theory, and the study of randomness. Work in this field is often distinguished by its emphasis on mathematical technique and rigor. Newsletters: Volume Issue Issue Date Number of Pages Actually Mailed 2014 45 01 March 2014 N/A 2013 44 04 December 2013 104 27-Dec-13 44 03 September 2013 96 30-Sep-13 44 02 June 2013 148 13-Jun-13 44 01 March 2013 116 18-Mar-13 2012 43 04 December 2012 140 29-Jan-13 43 03 September 2012 120 06-Sep-12 43 02 June 2012 144 25-Jun-12 43 01 March 2012 100 20-Mar-12 2011 42 04 December 2011 104 29-Dec-11 42 03 September 2011 108 29-Sep-11 42 02 June 2011 104 N/A 42 01 March 2011 140 23-Mar-11 2010 41 04 December 2010 128 15-Dec-10 41 03 September 2010 128 13-Sep-10 41 02 June 2010 92 17-Jun-10 41 01 March 2010 132 17-Mar-10 Membership: based on fiscal year dates 1st Year 2 + Years Total Year Professional -
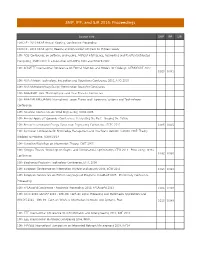
SNIP, IPP, and SJR 2014: Proceedings
SNIP, IPP, and SJR 2014: Proceedings Source title SNIP IPP SJR 10AIChE - 2010 AIChE Annual Meeting, Conference Proceedings 10AIChE - 2010 AIChE Spring Meeting and 6th Global Congress on Process Safety 10th ACIS Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, SNPD 2009, In conjunction with IWEA 2009 and WEACR 2009 10th ACM/IEEE International Conference on Formal Methods and Models for Codesign, MEMOCODE 2012 0.020 0.071 10th AIAA Aviation Technology, Integration and Operations Conference 2010, ATIO 2010 10th AIAA Multidisciplinary Design Optimization Specialist Conference 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference 10th Americas Conference on Wind Engineering, ACWE 2005 10th Annual Applied Ergonomics Conference: Celebrating the Past - Shaping the Future 10th Annual International Energy Conversion Engineering Conference, IECEC 2012 0.045 0.015 10th Australian Conference for Knowledge Management and Intelligent Decision Support 2007: Theory Wedded to Practice, ACKMIDS'07 10th Canadian Workshop on Information Theory, CWIT 2007 10th Cologne-Twente Workshop on Graphs and Combinatorial Optimization, CTW 2011 - Proceedings of the 0.032 0.030 Conference 10th Electronics Packaging Technology Conference, EPTC 2008 10th European Conference on Information Warfare and Security 2011, ECIW 2011 0.055 0.023 10th European Conference on Pattern Languages of Programs, EuroPLoP 2005 - Preliminary Conference Proceedings 10th FPGAworld Conference - Academic Proceedings 2013, FPGAworld 2013 0.066 0.100 10th ICETE 2013; SIGMAP 2013 - 10th Int. Conf. on Signal Processing and Multimedia Applications and WINSYS 2013 - 10th Int. Conf. on Wireless Information Networks and Systems, Proc. -

Middle-Schoolers Are Ready, Ready, Ready for Programming Adventure
A RESEARCH AND ALUMNI NEWS MAGAZINE DEPARTMENT OF COMPUTER SCIENCE BROWN UNIVERSITY Middle-Schoolers Are Ready, Ready, Ready for Programming Adventure Also inside: ■ CS Women Take Exception To Being Typecast ■ Tunnels, Bunkers and Nukes: My Underground Vacation Spring | Summer 2011 Van Hentenryck on their new books: Tom’s Notes from the Chair: Operating Systems in Depth: Design and Pro- the Latest News from gramming and Pascal’s Hybrid Optimization: The Ten Years of CPAIOR. My book Introduc- 115 Waterman tion to Computer Security (coauthored with Mi- chael Goodrich) was also recently published. We are thrilled to Greetings to all CS alums, supporters and add these three vol- friends. umes to the de- partment’s library The spring semester is flying by and the CIT is of faculty-penned bustling with activity. Wonderful things continue books. More on to happen in the department and I am thrilled Pascal and Tom’s to be able to share the highlights with you. books can be found As part of a review of all departments and cen- on page 14. ters being conducted by the university, our de- It is with mixed partment underwent a review late last semester. feelings that I announce the departures of Mi- We are encouraged that strengths were found in chael Black and Meinolf Sellmann. Both have all major dimensions of research, teaching, ad- moved on to exciting opportunities: Michael ministration, and outreach. Based on feedback is a Director of a newly established Max Planck from the reviewers and from the university’s Ac- Institute in Tübingen, Germany and Meinolf ademic Priorities Committee, we plan to broad- is the Group Leader of AI for Optimization at en the horizon of our strategic planning efforts IBM Research in Yorktown Heights, New York. -

Similarity Search: Algorithms for Sets and Other High Dimensional Data
Similarity Search: Algorithms for Sets and other High Dimensional Data Thomas Dybdahl Ahle Advisor: Rasmus Pagh Submitted: March 2019 ii Abstract We study five fundemental problems in the field of high dimensional algo- rithms, similarity search and machine learning. We obtain many new results, including: • Data structures with Las Vegas guarantees for `1-Approximate Near Neigh- bours and Braun Blanquet Approximate Set Similarity Search with perfor- mance matching state of the art Monte Carlo algorithms up to factors no(1). • “Supermajorities:” The first space/time tradeoff for Approximate Set Sim- ilarity Search, along with a number of lower bounds suggesting that the algorithms are optimal among all Locality Sensitive Hashing (LSH) data structures. • The first lower bounds on approximative data structures based on the Or- thogonal Vectors Conjecture (OVC). • Output Sensitive LSH data structures with query time near t + nr for out- putting t distinct elements, where nr is the state of the art time to output a single element and tnr was the previous best for t items. • A Johnson Lindenstrauss embedding with fast multiplication on tensors (a Tensor Sketch), with high probability guarantees for subspace- and near- neighbour-embeddings. Resumé Vi kommer ind på fem fundementale problemer inden for højdimensionelle algoritmer, similarity search og machine learning. Vi opdager mange nye resultater, blandt andet: • Datastrukturer med Las Vegas garantier for `1-Approksimativ Nær Nabo og Braun Blanquet Approksimativ Mængde-similaritetssøgning der matcher state of the art Monte Carlo algoritmer op til no(1) faktorer i køretid og plads. • “Kvalificerede flertal:” De første tid-/plads-trade-offs for Approksimativ Mængde-similaritetssøgning samt et antal nedre grænser der indikerer at algoritmerne er optimale inden for Locality Sensitive Hashing (LSH) data- strukturer. -
Submission Data for 2020-2021 CORE Conference Ranking Process International Colloquium on Automata Languages and Programming
Submission Data for 2020-2021 CORE conference Ranking process International Colloquium on Automata Languages and Programming Anca Muscholl, Artur Czumaj Conference Details Conference Title: International Colloquium on Automata Languages and Programming Acronym : ICALP Rank: A Requested Rank Rank: A* Recent Years Proceedings Publishing Style Proceedings Publishing: series Link to most recent proceedings: https://drops.dagstuhl.de/opus/portals/lipics/index.php?semnr=16154 Further details: ICALP proceedings have been published since 2015 in the high-quality open-access series LIPIcs (Leibniz International Proceedings in Informatics), in cooperation with Schloss Dagstuhl-Leibniz Center for Informatics. Until 2015 ICALP proceedings were published with LNCS. Most Recent Years Most Recent Year Year: 2019 URL: https://icalp2019.upatras.gr/ Location: Patras, Greece Papers submitted: 502 Papers published: 147 Acceptance rate: 29 Source for numbers: https://drops.dagstuhl.de/opus/volltexte/2019/10576/pdf/LIPIcs-ICALP-2019-0.pdf General Chairs Name: Christos Zaroliagis Affiliation: Univ. of Patras, Greece Gender: M H Index: 28 GScholar url: https://scholar.google.com/citations?hl=en&user=L3AQ8wkAAAAJ DBLP url: https://dblp.org/pid/z/CDZaroliagis.html Name: Sotiris Nicoletseas Affiliation: Univ. of Patras, Greece Gender: SELECT H Index: 40 GScholar url: https://scholar.google.com/citations?hl=en&user=hk2ylNwAAAAJ DBLP url: https://dblp.org/pid/n/SotirisENikoletseas.html Program Chairs 1 Name: Stefano Leonardi Affiliation: Sapienza University of Rome, Italy Gender: M H Index: 44 GScholar url: https://scholar.google.com/citations?hl=en&user=p5LCHHEAAAAJ DBLP url: https://dblp.org/pid/l/StefanoLeonardi.html Name: Christel Baier Affiliation: TU Dresden, Germany Gender: F H Index: 49 GScholar url: https://scholar.google.com/citations?user=p8sX7r0AAAAJ&hl=en&oi=ao DBLP url: https://dblp.org/pid/b/ChristelBaier.html Name: Paola Flocchini Affiliation: Univ. -

Thanassis Avgerinos
Thanassis Avgerinos Carnegie Mellon University Citizenship: Greek Department of Electrical and Office: CIC #2131A Computer Engineering Email: [email protected] 5000 Forbes Avenue, Homepage: www.ece.cmu.edu/~aavgerin Pittsburgh, Pennsylvania, USA Work Experience & Education 2014-Present Founder and Software Engineer at ForAllSecure, Inc. 2009-2014 Research Assistant, PhD in Electrical and Computer Engineering, Carnegie Mellon University. • Advisor: Prof. David Brumley. • Areas: Software Security & Program Analysis. • Committee: David Brumley, Virgil Gligor, Andr´ePlatzer, George Candea. • Dissertation Title: Exploiting Tradeoffs in Symbolic Execution for Identifying Security Bugs. 2013 Master of Science in Electrical and Computer Engineering, Carnegie Mellon University. • Areas: Software Security & Program Analysis, GPA 4.0. 2004-2009 Diploma in Electrical and Computer Engineering, National Technical University of Athens. • Major: Computer Science. • Minor: Computer Networks and Telecommunications. • Honors: Summa Cum Laude, GPA 9.86/10 (1st out of 600+ students). Dissertation: • Diploma Thesis: Automatic Refactoring of Erlang Programs. • Advisor: Prof. Kostis Sagonas. • Committee: Kostis Sagonas, Nikolaos Papaspyrou, Stathis Zachos Research Interests • Program Analysis and Verification. • Software Security. • Programming Language Theory, Design and Implementation. • Compilers, compilation techniques and optimizations. • Software Engineering. Publications [1] Alexandre Rebert, Sang Kil Cha, Thanassis Avgerinos, Jonathan Foote, David Warren, Gustavo Grieco, and David Brumley. Optimizing seed selection for fuzzing. In 23rd USENIX Security Symposium (USENIX Security 14). USENIX Association, August 2014. [2] Thanassis Avgerinos, Alexandre Rebert, Sang Kil Cha, and David Brumley. Enhancing symbolic exe- cution with veritesting. In Proceedings of the 36th International Conference on Software Engineering, June 2014. [3] Thanassis Avgerinos, Sang Kil Cha, Alexandre Rebert, Edward J. Schwartz, Maverick Woo, and David Brumley.