Tc-2019-106-AC2-Supplement.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Download Abstract Booklet Session 12
Abstract Volume 14th Swiss Geoscience Meeting Geneva, 18th – 19th November 2016 12. Cryospheric Sciences 428 12. Cryospheric Sciences M. Schwikowski, M. Heggli, M. Huss, J. Nötzli, Daniel Tobler Swiss Snow, Ice and Permafrost Society Symposium 12: Cryospheric Sciences TALKS: 12.1 Brauchli T., Trujillo E., Huwald H., Lehning M.: Snowmelt observations at the slope scale and implications for the catchment response using the Alpine3D model 12.2 Buri P., Steiner J.F., Miles E.S., Pellicciotti F.: Modelling backwasting of supraglacial ice cliffs over a debris- covered glacier, Nepalese Himalaya 12.3 Calonne N., Cetti C., Fierz C., van Herwijnen A., Jaggi M., Löwe H., Matzl M., Schmid L., Schneebeli M.: A unique time series of daily and weekly snowpack measurements at Weissfluhjoch, Davos, Switzerland 12.4 Frehner M., Amschwand D., Gärtner-Roer I.: Rockglacier flow law determined from deformation data and geomorphological indicators: An example from the Murtèl rockglacier (Engadin, SE Switzerland) 12.5 Ghirlanda A., Delaloye R., Kummert M., Staub B., Braillard L.: Destabilization of the Jegi rock glacier: historical development and ongoing crisis 12.6 Irarrazaval I., Mariethoz G., Herman F.: Geostatistical inversion of subglacial drainage system 12.7 Jouvet G., Weidmann Y., Seguinot J., Funk M., Abe T., Sakakibara D., Sugiyama S.: Initiation of a major calving event on Bowdoin Glacier captured by UAV photogrammetry 12.8 Lindner F., Walter F., Laske G.: Seismic monitoring of the 2016 outburst flood of Lac des Faverges on Glacier de la Plaine Morte -

Identification of Glacial Meltwater Runoff in a Karstic Environment Andits Implication for Present and Future Water Availability
Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2013 Identification of glacial meltwater runoff in a karstic environment andits implication for present and future water availability Finger, David ; Hugentobler, Andreas ; Huss, Matthias ; Voinesco, Alice ; Wernli, Hans ; Fischer, Daniela ; Weber, Eric ; Jeannin, Pierre-Yves ; Kauzlaric, Martina ; Wirz, Andrea ; Vennemann, Torsten ; Hüsler, Fabia ; Schädler, Bruno ; Weingartner, Rolf Abstract: Glaciers all over the world are expected to continue to retreat due to the global warming throughout the 21st century. Consequently, future seasonal water availability might become scarce once glacier areas have declined below a certain threshold affecting future water management strategies. Par- ticular attention should be paid to glaciers located in a karstic environment, as parts of the meltwater can be drained by underlying karst systems, making it difficult to assess water availability. In this study tracer experiments, karst modeling and glacier melt modeling are combined in order to identify flow paths in a high alpine, glacierized, karstic environment (Glacier de la Plaine Morte, Switzerland) and to investigate current and predict future downstream water availability. Flow paths through the karst un- derground were determined with natural and fluorescent tracers. Subsequently, geologic information and the findings from tracer experiments were assembled in a karst model. Finally, glacier melt projections driven with a climate scenario were performed to discuss future water availability in the area surrounding the glacier. The results suggest that during late summer glacier meltwater is rapidly drained through well-developed channels at the glacier bottom to the north of the glacier, while during low flow season meltwater enters into the karst and is drained to the south. -

Cretaceous Syn-Sedimentary Faulting in the Wildhorn Nappe (SW Switzerland)
Swiss J Geosci (2014) 107:223–250 DOI 10.1007/s00015-014-0166-8 Cretaceous syn-sedimentary faulting in the Wildhorn Nappe (SW Switzerland) G. L. Cardello • Neil S. Mancktelow Received: 25 August 2013 / Accepted: 2 September 2014 / Published online: 7 October 2014 Ó Swiss Geological Society 2014 Abstract During Cretaceous time, the area of the future subsequent sediments reflect a passive adaption to the pre- Helvetic nappes (Central Alps, south-western Switzerland) existing topography of the sea floor, established during the was part of a large ramp-type carbonate depositional sys- earlier tectonic movements. (4) Post-Maastrichtian north- tem on the European margin, in which the area of the directed tilt and erosion. In the Wildhorn Nappe, palaeo- Wildhorn Nappe was transitional to the more distal and fault activity most probably ended in the Early Maas- relatively deeper Ultrahelvetic basin. The Wildhorn Nappe trichtian rather than continuing into the Eocene. Until now, includes an Upper Cretaceous succession bearing clear the regional importance and magnitude of Late Cretaceous evidence for syn-sedimentary normal faulting, such as syn- extension has not been recognized in the Helvetic domain. sedimentary geometries related to well oriented NE-strik- This widespread event may be related to post-breakup ing faults, sedimentary dykes, lateral variations in the extensional tectonics along the European margin or, alter- thickness and facies of formations, anomalous and discor- natively but less likely, to lateral gravitational collapse of dant contacts corresponding to palaeo-escarpments, and the margin. slump folds. Four stages of syn-sedimentary fault activity have been recognized. (1) Post-Cenomanian disruption and Keywords Central Alps Á Helvetic nappes Á exhumation of the Schrattenkalk platform related to dis- Cretaceous extensional faults Á Post-breakup tectonics Á tributed normal faulting, which contributed to the initiation Carbonate depositional systems Á Multiple fault systems of karst erosion on topographic highs and sedimentation in topographic lows. -

JOURNAL 1975 We Stock Climbing Gear, Sleeping Bags, Duvets, Water- Proof Clothing
THE ASSOCIATION OF BRITISH MEMBERS OF THE SWISS ALPINE CLUB we can supply everything but the mountain! JOURNAL 1975 We stock Climbing Gear, Sleeping Bags, Duvets, Water- proof Clothing. Specialise in Backpacking Gear. Plus over 40 Tents suitable for mountain use: names like Karrimor, Clog, Stubai, Moac, Saunders, Blacks, Kastinger, Vango, CONTENTS Henri Lloyd, HeIly Hansen, Grenfell, Ultimate, Snowdon, Peck, Hawkins, Bonaiti Cassin, Simond, Viking, Troll, Optimus, Point Five, Mountain, G. & H., J. B. Salewa, M.S.R., Camptralls, Scarpa, Berghaus, Spider & Joanny. Diary for 1975 3 You will be dealing with experts—Les Holliwell is our technical adviser. Before buying your gear—write or phone Maurice Bennett 5 for our EXTRAORDINARY COMPETITIVE FREE PRICE LIST. Barclaycard/Access accepted. We have a large Mail British Columbia by K. Ft. Hindell 7 Order Department—most items immediate despatch with 7 day approval service. The High Tatra by E. Sondheimer 10 We have a special Contract Department for Club and A House in the Mountains by 0. St. John 13 Expedition orders. Two Alpine Meets 15 Arolla by A. N. Sperryn Meiringen by J. E. Coales 25 Kings Road, Brentwood, Essex, Tel: (STD 0277) 221259. Only 10 minutes from Brentwood Station ; 30 minutes from Association Activities 19 London's Liverpool Street Station (Southend Line). NMI moo MIN Association Accounts 26 Please send me a copy of your FREE Price List Members' Climbs 29 NAME List of Past ea Present Officers 49 ADDRESS Complete List of Members 51 SE MEM DIARY FOR 1975 22 January Lecture, The Rockies by Mrs. Sally Westmacott 8-9 February Northern Dinner Meet, Glenridding - Leader, W. -

Assessing the Sustainability of Water Governance Systems: The
This article was downloaded by: [83.76.88.41] On: 14 July 2014, At: 19:43 Publisher: Routledge Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37-41 Mortimer Street, London W1T 3JH, UK Journal of Environmental Planning and Management Publication details, including instructions for authors and subscription information: http://www.tandfonline.com/loi/cjep20 Assessing the sustainability of water governance systems: the sustainability wheel Flurina Schneiderabe, Mariano Bonriposid, Olivier Graefec, Karl Herwega, Christine Homewoodc, Matthias Hussc, Martina Kauzlaricb, Hanspeter Linigera, Emmanuel Reyb, Emmanuel Reynardd, Stephan Rista, Bruno Schädlerb & Rolf Weingartnerb a Centre for Development and Environment, University of Bern, Bern, Switzerland b Department of Geography and Oeschger Center for Climate Change Research, University of Bern, Bern, Switzerland c Geography Unit, Department of Geosciences, University of Fribourg, Fribourg, Switzerland d Institute of Geography and Sustainability, University of Lausanne, Géopolis, Lausanne, Switzerland e Decision Center for a Desert City, Julie Ann Wrigley Global Institute of Sustainability, Arizona State University, Tempe, AZ, USA Published online: 11 Jul 2014. To cite this article: Flurina Schneider, Mariano Bonriposi, Olivier Graefe, Karl Herweg, Christine Homewood, Matthias Huss, Martina Kauzlaric, Hanspeter Liniger, Emmanuel Rey, Emmanuel Reynard, Stephan Rist, Bruno Schädler & Rolf Weingartner (2014): Assessing the sustainability of water governance systems: the sustainability wheel, Journal of Environmental Planning and Management, DOI: 10.1080/09640568.2014.938804 To link to this article: http://dx.doi.org/10.1080/09640568.2014.938804 PLEASE SCROLL DOWN FOR ARTICLE Taylor & Francis makes every effort to ensure the accuracy of all the information (the “Content”) contained in the publications on our platform. -
Implications of Climate Change on Glacier De La Plaine Morte, Switzerland
Geogr. Helv., 68, 227–237, 2013 www.geogr-helv.net/68/227/2013/ doi:10.5194/gh-68-227-2013 © Author(s) 2013. CC Attribution 3.0 License. Implications of climate change on Glacier de la Plaine Morte, Switzerland M. Huss, A. Voinesco, and M. Hoelzle Department of Geosciences, University of Fribourg, Fribourg, Switzerland Correspondence to: M. Huss ([email protected]) Received: 15 May 2013 – Revised: 19 August 2013 – Accepted: 1 October 2013 – Published: 16 December 2013 Abstract. Changes in Switzerland’s climate are expected to have major impacts on glaciers, the hydrological regime and the natural hazard potential in mountainous regions. Glacier de la Plaine Morte is the largest plateau glacier in the European Alps and thus represents a particularly interesting site for studying rapid and far-reaching effects of atmospheric warming on Alpine glaciers. Based on detailed field observations combined with numerical modelling, the changes in total ice volume of Glacier de la Plaine Morte since the 1950s and the dynamics of present glacier mass loss are assessed. Future ice melt and changes in glacier runoff are computed using climate scenarios, and a possible increase in the natural hazard potential of glacier-dammed lakes around Plaine Morte over the next decades is discussed. This article provides an integrative view of the past, current and future retreat of an extraordinary Swiss glacier and emphasizes the implications of climate change on Alpine glaciers. 1 Introduction Glacier de la Plaine Morte, located on the main water divide between the Rhine and Rhone in the Bernese Alps, Glaciers are known as one of the most direct indicators of cli- is highly particular in different aspects. -

ROUTES DU BONHEUR Thermal Baths and Walking in the Swiss Mountains
My Route du Bonheur... - Suggestions of itineraries to discover the world... Switzerland ROUTES DU BONHEUR Thermal baths and walking in the Swiss mountains From Valais via the Gemmi Pass to the gentle Simmental and to the Plaine Morte plateau, this part if Switzerland is best discovered at a leisurely pace on foot. Experience waterfalls, mountain lakes, via ferrata, gorges and suspension footbridges ... the choice is yours! An amazing year-round backdrop from hot springs to glaciers ... 3 NIGHTS A concierge is at your service: Our houses can help you organize your transfers. from 4001 203 186 * ¥ 6,222.88* * Prix Total communiqué à titre indicatif au 09/28/2021, calculé sur la base de 2 personnes en chambre double pour un séjour du nombrede nuits indiqué sur cette page par établissement, hors activités conseillées, hors établissements non réservables en ligne et hors restaurants. ** Prix d'un appel local. 1 2 3 29 miles 26 miles My Route du Bonheur... - Suggestions of itineraries to discover the world... 1 CRANS-MONTANA 2 — 1 NIGHT ( 1 property available ) Hostellerie Du Pas de L’Ours Restaurant and hotel in the mountains. Skiing on the world-renowned slopes of Crans-Montana is not the only pleasure in store for you at this charming chalet. The wood façades have been well-preserved as well as the interior stone walls. With views of the snow-covered mountain peaks, the suites have open fireplaces and jacuzzis that serve as lovely compliments to the relaxing therapies offered by L’Alpage Spa. At the hotel’s gourmet restaurant, chef Franck Reynaud invites you to taste his creations in which “emotion” serves as a guiding force, while those desiring hearty cuisine will find what they seek at Bistrot des Ours. -

Water Use Management in Dry Mountains of Switzerland. the Case of Crans-Montana-Sierre Area
Publication of this book was made possible by TÁMOP-4.2.1/B-09/1/KONV-2010-0006 program entitled “Development of Scientifi c, Organisational and R&D Infrastructure at the University of West Hungary”. © Nyugat-magyarországi Egyetem, Sopron, 2012 The chapters of this volume were revised by: MARTIN GERZABEK ◾ University of Natural Resources and Life Sciences, Vienna, Austria QINGYAN MENG ◾ Chinese Academy of Sciences, Beijing, China EMMANUEL REYNARD ◾ University of Lausanne, Lausanne, Switzerland ALFRED TEISCHINGER ◾ University of Natural Resources and Life Sciences, Vienna, Austria FERENC LAKATOS ◾ University of West Hungary, Sopron, Hungary VINCE ÖRDÖG ◾ University of West Hungary, Sopron, Hungary KÁROLY RÉDEI ◾ Hungarian Forest Research Institute, Sárvár, Hungary ANIKÓ HIRKA ◾ Hungarian Forest Research Institute, Sárvár, Hungary MIKLÓS NEMÉNYI ◾ University of West Hungary, Sopron, Hungary ATTILA JÓZSEF KOVÁCS ◾ University of West Hungary, Sopron, Hungary BÁLINT HEIL ◾ University of West Hungary, Sopron, Hungary FERENC FACSKÓ ◾ University of West Hungary, Sopron, Hungary MÁRTA SÁNDOR ◾ University of West Hungary, Sopron, Hungary Cover photos: FERENC FACSKÓ, BÁLINT HEIL, ATTILA JÓZSEF KOVÁCS ISBN 978-963-19-7352-5 Nemzeti Tankönyvkiadó Zrt. a Sanoma company www.ntk.hu • Customer service: [email protected] • Telephone: +36 80 200 788 Responsible for publication: JÁNOS TAMÁS KISS chief executive offi cer Technical director: BABICSNÉ VASVÁRI ETELKA • Technical editor: NÁNDOR DOBÓ Cover design: ZOLTÁN JENEY • Proofreader: PATRICIA HUGHES Storing number: 42693 • Size: 35,75 (A/5) sheets • First edition, 2012 Water Use Management in Dry Mountains of Switzerland. The Case of Crans-Montana-Sierre Area Emmanuel REYNARD – Mariano BONRIPOSI University of Lausanne, Institute of Geography. Anthropole, CH–1015 Lausanne, Switzerland. -

Influence of Particulate Matter on Observed Albedo Reductions On
Infl uence of particulate matter on observed albedo reductions on Plaine Morte glacier, Swiss Alps Master’s Thesis Faculty of Science University of Bern presented by Eva Bühlmann 2011 Supervisor: Prof. Dr. Margit Schwikowski Paul Scherrer Institute and Oeschger Centre for Climate Change Research Co-Supervisor: Prof. Dr. Martin Hoelzle Department of Geosciences,University of Fribourg Advisor: Pierre-Alain Herren Paul Scherrer Institute and Oeschger Centre for Climate Change Research II Moulin on Plaine Morte glacier, Eva Bühlmann, 2010 III IV Table of contents Table of contents Summary . XI Zusammenfassung . .XIII 1. Introduction . .1 1.1. State of knowledge and research motivation . 2 1.2. Research questions . 5 1.3. Project design . 5 1.4. Thesis outline . 6 2. Basic terms, concepts and processes . .7 2.1. Energy balance and albedo of glaciers . 7 2.2. Cryoconite . 7 2.3. Atmospheric transport and deposition mechanisms of PM . 8 2.4. Sources of PM and their identifi cation . 8 2.5. Carbonaceous fraction of soot . 9 3. Study site . 11 3.1. Geographical setting . 11 3.2. Climate and meteorology . 11 3.3. Glaciology and hydrology . 11 3.4. Geology . 13 4. Methods . 15 4.1. Fieldwork . 15 4.1.1. Sampling procedure . 15 4.2. Albedo and spectral refl ectance measurements . 15 4.3. Sample extraction and preparation . 17 4.4. Standard snowpit analyses . 18 4.4.1. Reconstruction of snowpack . 18 4.4.2. Ion chromatography (IC) . 18 4.4.3. Isotope ratio mass spectrometry (IR-MS) . 19 4.5. Mineral dust analyses . 20 4.5.1. X-ray diff raction (XRD) . -

Downhill Only Club 2012
DHOjournal DOWNHILL ONLY CLUB 2012 DHOJournal•2012•1 Jungfrau at night Contents Front Cover: Front www.downhillonly.com DHOjournal 3 Editorial Freddie Whitelaw LIST OF ADVERTISERS 4 Disconnected Jottings 43 Alpia Sport Wengen Season 2011/2012 59 Altitude 9 Wengen Manager’s Report Sheridan Killwick 22 Amstutz 11 An Introduction to the next Wengen Manager Andrew Davies 63 Bikecation 12 Race Results 2011/12 8 Brechin Management Limited 17 President’s Report 2012 Max Davies 48 Central Sport 20 Coggins Report 2012 Bob Eastwood 63 Chalet Stella Alpina Racing 16 Coggins, Eagles & Adult Ski Courses 23 British Schoolboys Races Lauren Maynard 25 DHO Flat 26 British Schoolgirls Racing Anne Taylor & Sarah Robinson bc D & R Group 31 Racing & Training Ingrid Christophersen 53 Da Sina-Sina’s Pub 33 Amateur Inter Club Championship Liz Moore 19 DHO Merchandise 35 Wengen Worthies 1, Fredy Fuchs Freddie Whitelaw 64 Emily Holt/Roosi Huus 36 Flindall Apartment General 8 History of Ski Jumping 37 British Ski Racing Publicity Tim Ashburner 14 Hotel Caprice 39 The Expedition Freddie Whitelaw 53 Hotel Falken 44 Volcanic Skiing Phil Smith 29 Hotel Jungfraublick 47 Ski Touring Report Kit Erhardt 30 Hotel Sunstar 51 Ski Equipment over the years Ingie Christophersen ibc Imperial Hotels 54 The Shackelton Traverse Janey King 2 Jungfraubahn 61 The Hills Are Alive.... Robert Stewart 22 Männlichen Cablecar 65 Wengen Faces 36 Martin Gertsch 70 Obituaries 29 Mendelssohn Musicweek DHO Club News 2011 59 Oxfordshire Glass 74 Officers & Committee Members 43 Paterson/Eiger Residence -

Exploring Sustainability Through Stakeholders' Perspectives And
www.water-alternatives.org Volume 8 | Issue 2 Schneider, F. 2015. Exploring sustainability through stakeholders’ perspectives and hybrid water in the Swiss Alps. Water Alternatives 8(2): 280-296 Exploring Sustainability through Stakeholders’ Perspectives and Hybrid Water in the Swiss Alps Flurina Schneider Centre for Development and Environment, University of Bern, Bern; [email protected] ABSTRACT: Can the concept of water as a socio-natural hybrid and the analysis of different users’ perceptions of water advance the study of water sustainability? In this article, I explore this question by empirically studying sustainability values and challenges, as well as distinct types of water as identified by members of five water user groups in a case study region in the Swiss Alps. Linking the concept of water as a socio-natural hybrid with the different water users’ perspectives provided valuable insights into the complex relations between material, cultural, and discursive practices. In particular, it provided a clearer picture of existing water sustainability challenges and the factors and processes that hinder more sustainable outcomes. However, by focusing on relational processes and individual stakeholder perspectives, only a limited knowledge could be created regarding a) what a more sustainable water future would look like and b) how current unsustainable practices can be effectively transformed into more sustainable ones. I conclude by arguing that the concept of water as a socio-natural hybrid provides an interesting analytical tool for investigating sustainability questions; however, if it is to contribute to water sustainability, it needs to be integrated into a broader transdisciplinary research perspective that understands science as part of a deliberative and reflective process of knowledge co-production and social learning between all actor groups involved. -
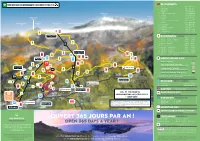
Ouvert 365 Jours Par an !
/ REJOIGNEZ MYCMA CLUB RESTAURANTS 1 Zérodix +41 27 481 00 90 2 Chez Erwin +41 79 479 78 09 3 Chetzeron +41 27 485 08 00 4 Merbé +41 27 485 89 84 Wildstrubel 5 Cry d’Er Club d’Altitude +41 27 485 89 85 3243 6 Arnouva +41 27 485 89 86 Rothorn Wildstrubel 7 Bar Seven +41 27 485 89 87 3102 Hüe 8 Pépinet +41 78 722 43 90 9 Cabane des Violettes (CAS) +41 27 481 39 19 Rohrbachstein Wisshore Gletscherhorn Glacier de Plaine-Morte 10 Violettes +41 27 485 89 88 2950 2948 2943 3000 11 Plaine Morte +41 27 485 89 89 12 Plumachit +41 27 481 25 32 13 Relais de Colombire +41 79 220 35 94 14 La Tièche +41 79 221 00 68 15 Cave du Scex +41 76 526 57 95 2 11 16 La Cure +41 27 481 04 98 1 PLAINE MORTE 2927 RANDONNÉES HIKING 1 Cry d’Er - Plaine Morte ** 3h25 2h50 2 Cry d’Er - Pochet - Violettes ** 1h40 1h45 3 Cry d’Er - Violettes 0h40 0h40 6 1 4 Cry d’Er - Montana 2h05 1h20 M 5 Cry d’Er - Crans 2h30 1h40 6 Violettes - Plaine Morte 2h10 1h25 7 Violettes - Montana ** 2h30 2h00 8 Violettes - Barzettes 2h00 1h25 LES VIOLETTES 2220 9 Marolires - Aminona (Bisse du Tsitorret) 2h05 1h05 2 14 9 ** parcours difficile | ** difficult route 5 1+2 3 CRY D’ER 9 10 MOUNTAIN BIKE & DH 2265 1 1 3 5 15 2 Downhill - Piste bleue DH blue trail 7+8 Mont-Lachaux Downhill – piste rouge 5 8 exclusivement vélo de descente | Distance : 3 km 13 DH red trail | Downhill bike exclusively | 3 km CHETZERON BUS GRATUIT 2100 DZ 1 L Chetzeron Downhill – piste noire exclusivement vélo de descente | Distance : 2.5 km DZ 1 SELFIE 7 4 DH black trail | Downhill bike exclusively | 2.5 km 12 16 9 Mountain Bike – piste verte | Distance : 2.5 km Mountain Bike - green trail | 2.5 km 3 8 4 CMA S.A.