Teacher's Guide
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Squaring the Circle a Case Study in the History of Mathematics the Problem
Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A. -

Circumference and Area of Circles 353
Circumference and 7-1 Area of Circles MAIN IDEA Find the circumference Measure and record the distance d across the circular and area of circles. part of an object, such as a battery or a can, through its center. New Vocabulary circle Place the object on a piece of paper. Mark the point center where the object touches the paper on both the object radius and on the paper. chord diameter Carefully roll the object so that it makes one complete circumference rotation. Then mark the paper again. pi Finally, measure the distance C between the marks. Math Online glencoe.com • Extra Examples • Personal Tutor • Self-Check Quiz in. 1234 56 1. What distance does C represent? C 2. Find the ratio _ for this object. d 3. Repeat the steps above for at least two other circular objects and compare the ratios of C to d. What do you observe? 4. Graph the data you collected as ordered pairs, (d, C). Then describe the graph. A circle is a set of points in a plane center radius circumference that are the same distance from a (r) (C) given point in the plane, called the center. The segment from the center diameter to any point on the circle is called (d) the radius. A chord is any segment with both endpoints on the circle. The diameter of a circle is twice its radius or d 2r. A diameter is a chord that passes = through the center. It is the longest chord. The distance around the circle is called the circumference. -

Unit 5 Area, the Pythagorean Theorem, and Volume Geometry
Unit 5 Area, the Pythagorean Theorem, and Volume Geometry ACC Unit Goals – Stage 1 Number of Days: 34 days 2/27/17 – 4/13/17 Unit Description: Deriving new formulas from previously discovered ones, the students will leave Unit 5 with an understanding of area and volume formulas for polygons, circles and their three-dimensional counterparts. Unit 5 seeks to have the students develop and describe a process whereby they are able to solve for areas and volumes in both procedural and applied contexts. Units of measurement are emphasized as a method of checking one’s approach to a solution. Using their study of circles from Unit 3, the students will dissect the Pythagorean Theorem. Through this they will develop properties of the special right triangles: 45°, 45°, 90° and 30°, 60°, 90°. Algebra skills from previous classes lead students to understand the connection between the distance formula and the Pythagorean Theorem. In all instances, surface area will be generated using the smaller pieces from which a given shape is constructed. The student will, again, derive new understandings from old ones. Materials: Construction tools, construction paper, patty paper, calculators, Desmos, rulers, glue sticks (optional), sets of geometric solids, pennies and dimes (Explore p. 458), string, protractors, paper clips, square, isometric and graph paper, sand or water, plastic dishpan Standards for Mathematical Transfer Goals Practice Students will be able to independently use their learning to… SMP 1 Make sense of problems • Make sense of never-before-seen problems and persevere in solving them. and persevere in solving • Construct viable arguments and critique the reasoning of others. -

On the Hawking Wormhole Horizon Entropy
ON THE HAWKING WORMHOLE HORIZON ENTROPY Hristu Culetu, Ovidius University, Dept.of Physics, B-dul Mamaia 124, 8700 Constanta, Romania e-mail : [email protected] November 11, 2018 Abstract The entropy S of the horizon θ = π/2 of the Hawking wormhole written in spherical Rindler coordinates is computed in this letter. Us- ing Padmanabhan’s prescription, we found that the surface gravity of the horizon is constant and equals the proper acceleration of the Rindler ob- server. S is a monotonic function of the radial coordinate ξ and vanishes when ξ equals the Planck length. In addition, its expression is similar with the Kaul-Majumdar one for the black hole entropy, including logarithmic corrections in quantum gravity scenarios. Keywords : surface gravity, spherical Rindler coordinates, horizon entropy. PACS Nos : 04.60 - m ; 02.40.-k ; 04.90.+e. 1 Introduction The connection between gravity and thermodynamics is one of the most sur- arXiv:hep-th/0409079v4 14 Apr 2006 prising features of gravity. Once the geometrical meaning of gravity is accepted, surfaces which act as one-way membranes for information will arise, leading to some connection with entropy, interpreted as the lack of information [1] [2]. As T.Padmanabhan has noticed [3], in any spacetime we might have a family of observers following a congruence of timelike curves which have no access to part of spacetime (a horizon is formed which blocks the informations from those observers). Keeping in mind that QFT does not recognize any nontrivial geometry of space- time in a local inertial frame, we could use a uniformly accelerated frame (a local Rindler frame) to study the connection between one way membranes arising in a spacetime and the thermodynamical entropy. -

The Method of Exhaustion
The method of exhaustion The method of exhaustion is a technique that the classical Greek mathematicians used to prove results that would now be dealt with by means of limits. It amounts to an early form of integral calculus. Almost all of Book XII of Euclid’s Elements is concerned with this technique, among other things to the area of circles, the volumes of tetrahedra, and the areas of spheres. I will look at the areas of circles, but start with Archimedes instead of Euclid. 1. Archimedes’ formula for the area of a circle We say that the area of a circle of radius r is πr2, but as I have said the Greeks didn’t have available to them the concept of a real number other than fractions, so this is not the way they would say it. Instead, almost all statements about area in Euclid, for example, is to say that one area is equal to another. For example, Euclid says that the area of two parallelograms of equal height and base is the same, rather than say that area is equal to the product of base and height. The way Archimedes formulated his Proposition about the area of a circle is that it is equal to the area of a triangle whose height is equal to it radius and whose base is equal to its circumference: (1/2)(r · 2πr) = πr2. There is something subtle here—this is essentially the first reference in Greek mathematics to the length of a curve, as opposed to the length of a polygon. -

COBE Satellite Measurement\ Hyperspheres\ Superstrings and the Dimension of Spacetime
Chaos\ Solitons + Fractals Vol[ 8\ No[ 7\ pp[ 0334Ð0360\ 0887 Þ 0887 Elsevier Science Ltd[ All rights reserved Pergamon Printed in Great Britain \ 9859Ð9668:87 ,08[99¦9[99 PII] S9859!9668"87#99019!8 COBE Satellite Measurement\ Hyperspheres\ Superstrings and the Dimension of Spacetime M[ S[ EL NASCHIE DAMTP\ Cambridge\ U[K[ "Accepted 10 April 0887# Abstract*The _rst part of the paper attempts to establish connections between hypersphere backing in in_nite dimensions\ the expectation value of dim E"# spacetime and the COBE measurement of the microwave background radiation[ One of the main results reported here is that the mean sphere in S"# spans a four dimensional manifold and is thus equal to the expectation value of the topological dimension of E"#[ In the second part we introduce within a general theory\ a probabolistic justi_cation for a com! pacti_cation which reduces an in_nite dimensional spacetime E"# "n# to a four dimensional one "# 2 "DTn3#[ The e}ective Hausdor} dimension of this space is given by ðdimH E ŁdH3¦f where f20:ð3¦f2Ł is a PV number and f"z4−0#:1 is the Golden Mean[ The derivation makes use of various results from knot theory\ four manifolds\ noncommutative geometry\ quasi periodic tiling and Fredholm operators[ In addition some relevant analogies between E"#\ statistical mechanics and Jones polynomials are drawn[ This allows a better insight into the nature of the proposed compacti_cation\ the associated E"# space and the Pisot!Vijayvaraghavan number 0:f23[125956866 representing it|s dimension[ This dimension is -

Math2 Unit6.Pdf
Student Resource Book Unit 6 1 2 3 4 5 6 7 8 9 10 ISBN 978-0-8251-7340-0 Copyright © 2013 J. Weston Walch, Publisher Portland, ME 04103 www.walch.com Printed in the United States of America WALCH EDUCATION Table of Contents Introduction. v Unit 6: Circles With and Without Coordinates Lesson 1: Introducing Circles . U6-1 Lesson 2: Inscribed Polygons and Circumscribed Triangles. U6-43 Lesson 3: Constructing Tangent Lines . U6-85 Lesson 4: Finding Arc Lengths and Areas of Sectors . U6-106 Lesson 5: Explaining and Applying Area and Volume Formulas. U6-121 Lesson 6: Deriving Equations . U6-154 Lesson 7: Using Coordinates to Prove Geometric Theorems About Circles and Parabolas . U6-196 Answer Key. AK-1 iii Table of Contents Introduction Welcome to the CCSS Integrated Pathway: Mathematics II Student Resource Book. This book will help you learn how to use algebra, geometry, data analysis, and probability to solve problems. Each lesson builds on what you have already learned. As you participate in classroom activities and use this book, you will master important concepts that will help to prepare you for mathematics assessments and other mathematics courses. This book is your resource as you work your way through the Math II course. It includes explanations of the concepts you will learn in class; math vocabulary and definitions; formulas and rules; and exercises so you can practice the math you are learning. Most of your assignments will come from your teacher, but this book will allow you to review what was covered in class, including terms, formulas, and procedures. -
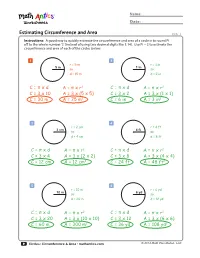
Estimating Circumference and Area
® Name: Date: Estimating Circumference and Area CCA 1 Instructions: A good way to quickly estimate the circumference and area of a circle is to round Pi off to the whole number ‘3’ (instead of using two decimal digits like 3.14). Use Pi = 3 to estimate the circumference and area of each of the circles below. 1 2 r = 5 m r = 1 in 5 m 1 in so so d = 10 m d = 2 in C = π x d A = π x r2 C = π x d A = π x r2 C = 3 x 10 A = 3 x (5 x 5) C = 3 x 2 A = 3 x (1 x 1) C = 30 m A = 75 m2 C = 6 in A = 3 in2 3 4 r = 2 cm r = 4 ft 2 cm 4 ft so so d = 4 cm d = 8 ft C = π x d A = π x r2 C = π x d A = π x r2 C = 3 x 4 A = 3 x (2 x 2) C = 3 x 8 A = 3 x (4 x 4) C = 12 cm A = 12 cm2 C = 24 ft A = 48 ft2 5 6 r = 10 m r = 6 yd 10 m 6 yd so so d = 20 m d = 12 yd C = π x d A = π x r2 C = π x d A = π x r2 C = 3 x 20 A = 3 x (10 x 10) C = 3 x 12 A = 3 x (6 x 6) C = 60 m A = 300 m2 C = 36 yd A = 108 yd2 Circles: Circumference & Area • mathantics.com © 2014 Math Plus Motion, LLC ® Name: Date: Calculating Circumference CCA 2 Instructions: Use the formula you learned in the video to calculate the circumference of each circle below. -

Maths Module 7 Geometry
Maths Module 7 Geometry This module covers concepts such as: • two and three dimensional shapes • measurement • perimeter, area and volume • circles www.jcu.edu.au/students/learning-centre Module 7 Geometry 1. Introduction 2. Two Dimensional Shapes 3. Area and Perimeter 4. Circles 5. Three Dimensional Shapes 6. Measurement 7. Area and Volume (extension) 8. Answers 9. Helpful Websites 2 1. Introduction Geometry exists in the world around us both in manmade and natural form. This first section covers some aspects of plane geometry such as lines, points, angles and circles. A point marks a point, a position, yet is does not have a size. However, physically, when we draw a point it will have width, but as an abstract concept, it really represents a point in our imagination. A line also has no width; it will extend infinitely in both directions. When drawing a line, physically it has width, yet it is an abstract representation in our minds. Given two distinct points for a line to pass though – there will only ever be the one line. The points are generally referred to with upper case letters and the line with lower case. For instance we may draw line though points and : The line may be referred to as line or as line . The distance between and is called a line segment or interval. If we had two lines, there would be two possibilities. They would either meet at a single point, and they would form angles at the intersection. Or they would never meet, and then they would be parallel lines. -

SPACETIME & GRAVITY: the GENERAL THEORY of RELATIVITY
1 SPACETIME & GRAVITY: The GENERAL THEORY of RELATIVITY We now come to one of the most extraordinary developments in the history of science - the picture of gravitation, spacetime, and matter embodied in the General Theory of Relativity (GR). This theory was revolutionary in several di®erent ways when ¯rst proposed, and involved a fundamental change how we understand space, time, and ¯elds. It was also almost entirely the work of one person, viz. Albert Einstein. No other scientist since Newton had wrought such a fundamental change in our understanding of the world; and even more than Newton, the way in which Einstein came to his ideas has had a deep and lasting influence on the way in which physics is done. It took Einstein nearly 8 years to ¯nd the ¯nal and correct form of the theory, after he arrived at his 'Principle of Equivalence'. During this time he changed not only the fundamental ideas of physics, but also how they were expressed; and the whole style of theoretical research, the relationship between theory and experiment, and the role of theory, were transformed by him. Physics has become much more mathematical since then, and it has become commonplace to use purely theoretical arguments, largely divorced from experiment, to advance new ideas. In what follows little attempt is made to discuss the history of this ¯eld. Instead I concentrate on explaining the main ideas in simple language. Part A discusses the new ideas about geometry that were crucial to the theory - ideas about curved space and the way in which spacetime itself became a physical entity, essentially a new kind of ¯eld in its own right. -

Class 6: Curved Space and Metrics
Class 6: Curved Space and Metrics In this class we will discuss the meaning of spatial curvature, how distances in a curved space can be measured using a metric, and how this is connected to gravity Class 6: Curved Space and Metrics At the end of this session you should be able to … • … describe the geometrical properties of curved spaces compared to flat spaces, and how observers can determine whether or not their space is curved • … know how the metric of a space is defined, and how the metric can be used to compute distances and areas • ... make the connection between space-time curvature and gravity • … apply the space-time metric for Special Relativity and General Relativity to determine proper times and distances Properties of curved spaces • In the last Class we discussed that, according to the Equivalence Principle, objects “move in straight lines in a curved space-time”, in the presence of a gravitational field • So, what is a straight line on a curved surface? We can define it as the shortest distance between 2 points, which mathematicians call a geodesic https://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/non_Euclid_curved/index.html https://www.quora.com/What-are-the-reasons-that-flight-paths-especially-for-long-haul-flights-are-seen-as-curves-rather-than-straight-lines-on-a- screen-Is-map-distortion-the-only-reason-Or-do-flight-paths-consider-the-rotation-of-the-Earth Properties of curved spaces Equivalently, a geodesic is a path that would be travelled by an ant walking straight ahead on the surface! • Consider two -

Lesson 17: the Area of a Circle
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 17 7•3 Lesson 17: The Area of a Circle Student Outcomes . Students give an informal derivation of the relationship between the circumference and area of a circle. Students know the formula for the area of a circle and use it to solve problems. Lesson Notes . Remind students of the definitions for circle and circumference from the previous lesson. The Opening Exercise is a lead-in to the derivation of the formula for the area of a circle. Not only do students need to know and be able to apply the formula for the area of a circle, it is critical for them to also be able to draw the diagram associated with each problem in order to solve it successfully. Students must be able to translate words into mathematical expressions and equations and be able to determine which parts of the problem are known and which are unknown or missing. Classwork Exercises 1–3 (4 minutes) Exercises 1–3 Solve the problem below individually. Explain your solution. 1. Find the radius of a circle if its circumference is ퟑퟕ. ퟔퟖ inches. Use 흅 ≈ ퟑ. ퟏퟒ. If 푪 = ퟐ흅풓, then ퟑퟕ. ퟔퟖ = ퟐ흅풓. Solving the equation for 풓, ퟑퟕ. ퟔퟖ = ퟐ흅풓 ퟏ ퟏ ( ) ퟑퟕ. ퟔퟖ = ( ) ퟐ흅풓 ퟐ흅 ퟐ흅 ퟏ (ퟑퟕ. ퟔퟖ) ≈ 풓 ퟔ. ퟐퟖ ퟔ ≈ 풓 The radius of the circle is approximately ퟔ 퐢퐧. 2. Determine the area of the rectangle below. Name two ways that can be used to find the area of the rectangle. The area of the rectangle is ퟐퟒ 퐜퐦ퟐ.