DOCSLIB.ORG

This Topic Will Be Treated Again in Our Next Issue. and in the Issue After

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
This Topic Will Be Treated Again in Our Next Issue. and in the Issue After e: The Master of All BRIAN J. MCCARTIN Read Euler, read Euler. He is the master of us all. --P. S. de Laplace aplace's dictum may rightfully be transcribed as: "Study Thus, e was first conceived as the limit e, study e. It is the master of all." L e = lim (1 + l/n)*' = 2.718281828459045" (1) Just as Gauss earned the moniker Princeps mathemati- n~ao corum amongst his contemporaries [1], e may be dubbed although its baptism awaited Euler in the eighteenth cen- Princeps constantium symbolum. Certainly, Euler would tury [2]. One might naively expect that all that could be concur, or why would he have endowed it with his own gleaned from equation (1) would have been mined long initial [2]? ago. Yet, it was only very recently that the asymptotic The historical roots of e have been exhaustively traced development and are readily available [3, 4, 5]. Likewise, certain funda- mental properties of e such as its limit definition, its series =(1+1/n) ~ = ~ e~. representation, its close association with the rectangular hy- perbola, and its relation to compound interest, radioactive decay, and the trigonometric and hyperbolic functions are ev= e l---7--. ' (2) k=o (v+ k)! l=o too well known to warrant treatment here [6, 7]. Rather, the focus of the present article is on matters re- with & denoting the Stirling numbers of the first kind [9], lated to e which are not so widely appreciated or at least was discovered [10]. have never been housed under one roof. When I do in- Although equation (1) is traditionally taken as the defin- dulge in reviewing well-known facts concerning e, it is to ition of e, it is much better approximated by the limit forge a link to results of a more exotic variety. [ (n + 2)n+2 (n + l)n+l ] Occurrences of e throughout pure and applied mathe- e = n--+~lim (n + 1),,+i r/n (3) matics are considered; exhaustiveness is not the goal. Nay, the breadth and depth of our treatment of e has been cho- discovered by Brothers and Knox in 1998 [11]. Figure 1 dis- sen to convey the versatility of this remarkable number and plays the sequences involved in equations (1) and (3). The to whet the appetite of the reader for further investigation. superior convergence of equation (3) is apparent. In light of the fact that both equations (1) and (3) pro- The Cast vide rational approximations to e, it is interesting to note Unlike its elder sibling ~r, e cannot be traced back through that 87~ = 2.71826 provides the best rational approxirna- 323 the mists of time to some prehistoric era [8]. Rather, e burst tion to e, with a numerator and denominator of fewer than into existence in the early seventeenth century in the con- four decimal digits [12]. (Note the palindromes!) Consider- text of commercial transactions involving compound inter- ing that the fundamental constants of nature (speed of light est [5]. Unnamed usurers observed that the profit from in- in vacuo, mass of the electron, Planck's constant, and so terest increased with increasing frequency of compounding, on) are known reliably to only six decimal digits, this is re- but with diminishing returns. markable accuracy indeed. Mystically, if we simply delete 10 THE MATHEMATICAL INTELLIGENCER 2006 Springer Science+Business Media, Inc. 1 i i i i i i 6 o 0 0 0 0 2.7 l e 2.6 2.5 2.4 = Eq. 1 o= Eq. 3 2.3 2.2 2.1 2 i i I i I 1 I I I 2 4 6 8 10 12 14 16 18 20 n Figure I. Exponential sequences. the last digit of both numerator and denominator then we ~, 2k+2 t~ s732, the best rauonal" approximation to e using fewer e = (5) k=0 (2k)! han three digits [13]. Is this to be regarded as a singular property of e or of base 10 numeration? Figure 2 displays the partial sums of equations (4) and (5) In 1669, Newton published the famous series represen- and clearly reveals the enhanced rate of convergence. A va- tation for e [14], riety of series-based approximations to e are offered in [15]. Euler discovered a number of representations of e by con- e---= 2 ~t1 = tinued fractions. There is the simple continued fraction [16] k 0 1 1 1 1 1 1+1+ ~.(1+ ~-.(1+ ~-.(1+ ~-.(1+ .'')))), (4) e = 2 + 1 , (6) 1+ 2+ 11 established by application of the binomial expansion to 1+ 1 1+ 4+ l+.__.k~_~1 equation (1). Many more rapidly convergent series repre- 1+ r~... sentations have been devised by Brothers [14] such as or the more visually alluring [5] BRIAN J. McCARTIN studied Applied Mathe- matics at the University of Rhode Island and e = 2 + 1 (7) went on to a Ph.D. at the Courant Institute, 1 + 2+-- 2 8 3+ New York University. He was Senior Research 4+ 4 5+6+ 0 6 7 Mathematician for United Technologies Re- 7+8+... search Center and Chair of Computer Science at RPI/Hartford before joining Kettenng Univer- In 1655, John Wallis published the exhilarating infinite sity in 1993. He received the Distinguished product Teaching Award from the Michigan Section of rr 2244668810101212141416 the MAA in 2004. Along the way, he also ................. (8) 2 133557799111113131515 eamed a degree in music from the University of Hartford (1994). To fill in the details see However, the world had to wait until 1980 for the "Pip- http://www.ketted ng,edu/- bmccarti. penger product" [17] Applied Mathematics e Kettering University 2 Flint, MI,' 48504-4808 USA \l J\ 3! \5 5 7 7/\ 9 9 11 11 13 13 15 ~/ '''. (9) 9 2006Springer Science+Business Media, Inc, Volume 28, Number 2, 2006 1 1 2.8 i i i i i i O O Q o Q t o 2.6 e 2.4 2.2 = Eq. (4) o = Eq. (5) 1.8 1.6 1.4 1.2 1 I f I I I I 0 1 2 3 4 5 6 n Figure 2. Exponential series. In spite of their beauty, equations (8) and (9) converge Barel-e Transcendental very slowly. A product representation for e which converges As noted above, e is transcendental, but just barely so [21, at the same rate as equation (4) is given by [18] 22]. In 1844, Liouville proved that the degree to which an algebraic irrational number can be approximated by ratio- U 1 ----- 1; Un+ 1 = (T/ 4- 1)(Un -I- 1) nals is limited [23], so that, from the point of view of ratio- [I un+ 1 2 5 16 65 326 nal approximation, the simplest numbers are the worst [24]. e ........... (10) n=l U*I 1 4 15 64 325 Liouville used this property--that if an irrational number is rapidly approximated by rationals then it must be transcen- An Interesting Inequalit-e dental-to construct the first known transcendental number, In 1744, Euler showed that e is irrational by considering the the so-called Liouville number L = 10 -1! + 10 -2! + 10 -3! 4- simple infinite continued fraction (6) [19]. In 1840, .. 10-m! + -. In 1955, Klaus Roth provided the defini- Liouville showed that e was not a quadratic irrational. Finally, tive refinement of Liouville's theorem by finding the ulti- in 1873, Hermite showed that e is in fact transcendental. mate limit to which algebraic irrationals may be approxi- Since then, Gelfond has shown that e ~ is also transcen- mated by rationals [19]. For this work, he was awarded the dental. Although now known as Gelfond's constant, this Fields Medal in 1958. number had previously attracted the attention of the influ- To phrase these results quantitatively, for any real num- ential nineteenth-century American mathematician Benjamin ber 0 < s~ < 1 and any fraction p/q in lowest terms, let R Peirce, who was wont to write on the blackboard the fol- denote the set of all positive real numbers r for which the lowing alteration of Euler's identity [2, 5]: inequality '= ~e ~, (11) 1 0 < I~ -- P l < qr (14) then turn to the class and cryptically remark, "Gentlemen, we have not the slightest idea what this equation means, but we possesses at most finitely many solutions. Then, define the may be sure that it means something very important" [4]. Liouville-Roth constant (irrationality measure) as But what of ~r~? Well, it is not even known whether it is rational! Niven [20] playfully posed the question "Which is r(~ ~- inf r, (15) larger, e ~r or rre?''. Not only did he provide the answer r~R e ~ > ITe, (12) that is, the critical rate threshold above which {: is not ap- proximable by rationals. he also established the more general inequalities Then, the above may be summarized as follows [22]: /3>a->e~ c~/3>/3~; e->/3>a>0~/3~>~/3, (13) {i: when {: is rati~ where e plays a pivotal role. This result is displayed graph- r(~ = when {: is algebraic of degree > 1, (16) ically in Figure 3. 2 when s~ is transcendental. 12 THE MATHEMATICALINTELLIGENCER xY-yX=O 10 I i I I I I I 9=i "/ >0 7 I 6 >, 5 4 <0 <0 3 (e,e) 2 >0 0 i I I I I I I I 0 1 2 3 4 5 6 7 8 10 x Figure 3. e" > ~'~. 2.8 I I I i I ,e..- e 2.6 2.41 2.2 2 1.8 1.6 1.4 = i i f i 0 1000 2000 3000 4000 5000 6000 n Figure 4.
Load more

Recommended publications
  • Liouville Numbers
    Math 154 Notes 2 In these notes I’ll construct some explicit transcendental numbers. These numbers are examples of Liouville numbers. Let {ak} be a sequence of positive integers, and suppose that ak divides ak+1 for all k. We say that {ak} has moderate growth if there is some con- K stant K such that an+1 <K(an) for all n. Otherwise we say that {an} has immoderate growth. ∞ 1 Theorem 0.1 k P If {a } has immoderate growth then the number x = n=1 an is transcendental. Proof: We will suppose that P (x) = 0 for some polynomial P . There is some constant C1 such that P has degree at most C1 and all the coefficients of P are less than C1 in absolute value. Let xn = 1/a1 + ... +1/an. The divisibility condition guarantees that xn = hn/an, where hn is some integer. As long as P (xn) is nonzero, we have −C1 |P (xn) − P (x)| = |P (xn)|≥ (an) . (1) This just comes from the fact that P (xn) is a rational number whose denom- C1 inator is at most (an) . ′ On the other hand, there is some constant C2 such that |P (u)| < C2 for all u in the interval [x − 1,x + 1]. For n large, xn lies in this interval. Therefore, by the usual estimate that comes from integration, −1 |P (xn) − P (x)| <C2|xn − x| < 2C2an+1. (2) The last inequality comes from the fact that {1/an} decays faster than the sequence {1/2n} once n is large.
    [Show full text]
  • Irrationality and Transcendence of Alternating Series Via Continued
    Mathematical Assoc. of America American Mathematical Monthly 0:0 October 1, 2020 12:43 a.m. alternatingseries.tex page 1 Irrationality and Transcendence of Alternating Series Via Continued Fractions Jonathan Sondow Abstract. Euler gave recipes for converting alternating series of two types, I and II, into equiv- alent continued fractions, i.e., ones whose convergents equal the partial sums. A condition we prove for irrationality of a continued fraction then allows easy proofs that e, sin 1, and the pri- morial constant are irrational. Our main result is that, if a series of type II is equivalent to a sim- ple continued fraction, then the sum is transcendental and its irrationality measure exceeds 2. ℵℵ0 = We construct all 0 c such series and recover the transcendence of the Davison–Shallit and Cahen constants. Along the way, we mention π, the golden ratio, Fermat, Fibonacci, and Liouville numbers, Sylvester’s sequence, Pierce expansions, Mahler’s method, Engel series, and theorems of Lambert, Sierpi´nski, and Thue-Siegel-Roth. We also make three conjectures. 1. INTRODUCTIO. In a 1979 lecture on the Life and Work of Leonhard Euler, Andr´eWeil suggested “that our students of mathematics would profit much more from a study of Euler’s Introductio in Analysin Infinitorum, rather than of the available mod- ern textbooks” [17, p. xii]. The last chapter of the Introductio is “On Continued Frac- tions.” In it, after giving their form, Euler “next look[s] for an equivalent expression in the usual way of expressing fractions” and derives formulas for the convergents. He then converts a continued fraction into an equivalent alternating series, i.e., one whose partial sums equal the convergents.
    [Show full text]
  • Tracing Objects of Measurement: Locating Intersections of Race, Science and Politics at Stellenbosch University
    TRACING OBJECTS OF MEASUREMENT: LOCATING INTERSECTIONS OF RACE, SCIENCE AND POLITICS AT STELLENBOSCH UNIVERSITY Handri Walters Thesis presented in fulfilment of the requirements for the degree of Doctor of Philosophy in Social Anthropology in the Faculty of Arts and Social Sciences at Stellenbosch University Supervisor: Professor Kees (C.S.) van der Waal Co-Supervisor: Professor Steven Robins March 2018 Stellenbosch University https://scholar.sun.ac.za i Stellenbosch University https://scholar.sun.ac.za DECLARATION By submitting this thesis electronically, I declare that the entirety of the work contained therein is my own, original work, that I am the sole author thereof (save to the extent explicitly otherwise stated), that reproduction and publication thereof by Stellenbosch University will not infringe any third party rights and that I have not previously in its entirety or in part submitted it for obtaining any qualification. March 2018 Copyright © 2018 Stellenbosch University All rights reserved i Stellenbosch University https://scholar.sun.ac.za ii Stellenbosch University https://scholar.sun.ac.za ABSTRACT This study departs from a confrontation with a collection of ‘scientific’ objects employed at Stellenbosch University in various ways from 1925 to 1984. Eugen Fischer’s Haarfarbentafel (hair colour table), Rudolf Martin’s Augenfarbentafel (eye colour table) and Felix von Luschan’s Hautfarbentafel (skin colour table) - a collection later joined by an anatomically prepared human skull - are employed in this study as vessels for
    [Show full text]
  • Using Groups Statistics to Sentence Individual Criminals: an Ethical and Statistical Critique of the Virginia Risk Assessment Program Brian Netter
    Journal of Criminal Law and Criminology Volume 97 Article 1 Issue 3 Spring Spring 2007 Using Groups Statistics to Sentence Individual Criminals: An Ethical and Statistical Critique of the Virginia Risk Assessment Program Brian Netter Follow this and additional works at: https://scholarlycommons.law.northwestern.edu/jclc Part of the Criminal Law Commons, Criminology Commons, and the Criminology and Criminal Justice Commons Recommended Citation Brian Netter, Using Groups Statistics to Sentence Individual Criminals: An Ethical and Statistical Critique of the Virginia Risk Assessment Program, 97 J. Crim. L. & Criminology 699 (2006-2007) This Criminal Law is brought to you for free and open access by Northwestern University School of Law Scholarly Commons. It has been accepted for inclusion in Journal of Criminal Law and Criminology by an authorized editor of Northwestern University School of Law Scholarly Commons. 0091-4169107/9703-0699 TIm, JOURNALOF CRIMINAL LAW& CRIMINOLOGY Vol. 97, No. 3 Copyright © 2007 by Northwestem University, School of Law Printed inU.S.A. CRIMINAL LAW USING GROUP STATISTICS TO SENTENCE INDIVIDUAL CRIMINALS: AN ETHICAL AND STATISTICAL CRITIQUE OF THE VIRGINIA RISK ASSESSMENT PROGRAM BRIAN NETTER* Virginia's program of nonviolent offender risk assessment uses predictions of recidivism to recommend which felons should be incarcerated. Unlike many sentencing schemes that rely upon the severity of the offense and the offender's criminal history, Viginia's depends on a statistical study commissioned by the legislature that purports to match offender characteristics with future behavior. New offenders are given recidivism "scores" that depend on gender, employment status, marital status, and age-all factors seemingly unrelated to the criminal conduct itself This Essay criticizes the Virginia approach as ethically suspect and mathematically unsound and calls for greater public discourse as to the hidden assumptions underlying the sentencing apparatus.
    [Show full text]
  • On Transcendental Numbers: New Results and a Little History
    Axioms 2013, xx, 1-x; doi:10.3390/—— OPEN ACCESS axioms ISSN 2075-1680 www.mdpi.com/journal/axioms Communication On transcendental numbers: new results and a little history Solomon Marcus1 and Florin F. Nichita1,* 1 Institute of Mathematics of the Romanian Academy, 21 Calea Grivitei Street, 010702 Bucharest, Romania * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel: (+40) (0) 21 319 65 06; Fax: (+40) (0) 21 319 65 05 Received: xx / Accepted: xx / Published: xx Abstract: Attempting to create a general framework for studying new results on transcendental numbers, this paper begins with a survey on transcendental numbers and transcendence, it then presents several properties of the transcendental numbers e and π, and then it gives the proofs of new inequalities and identities for transcendental numbers. Also, in relationship with these topics, we study some implications for the theory of the Yang-Baxter equations, and we propose some open problems. Keywords: Euler’s relation, transcendental numbers; transcendental operations / functions; transcendence; Yang-Baxter equation Classification: MSC 01A05; 11D09; 11T23; 33B10; 16T25 arXiv:1502.05637v2 [math.HO] 5 Dec 2017 1. Introduction One of the most famous formulas in mathematics, the Euler’s relation: eπi +1=0 , (1) contains the transcendental numbers e and π, the imaginary number i, the constants 0 and 1, and (transcendental) operations. Beautiful, powerful and surprising, it has changed the mathematics forever. We will unveil profound aspects related to it, and we will propose a counterpart: ei π < e , (2) | − | Axioms 2013, xx 2 Figure 1. An interpretation of the inequality ei π < e .
    [Show full text]
  • Adolphe Quetelet and the Development of Economic
    Adolphe Quetelet, the Average Man and the Development of Economic Methodology1 Bert Mosselmans2 Abstract Quetelet's contribution to statistics has received adequate attention in Stigler (1986, 1999) and Porter's (1986) seminal works on the history of that scientific discipline.3 Our contribution investigates Quetelet's influence on economic methodology. Other scholars have already investigated his influence on econometrics and empirical economics (Morgan 1990, Stigler 1999), but we argue that his influence on theoretical economics should be considered significant as well. We devote attention to Quetelet’s concept of the ‘average man’. For this purpose we briefly summarize Quetelet's methodology and examine the evolution of his ideas as expressed in his published works. We then investigate his influence on classical political economy, on Jevons’s ‘calculus of pleasures and pains’ and on the debates of the ‘Methodenstreit’. We conclude with some considerations on contemporary discussions in macroeconomics about the ‘representative individual’. We argue that the history of statistics, and especially Quetelet's contribution, should not be neglected by historians of economic thought as it provides important insights into the development of economic methodology. 1 Previous versions of this paper have been presented at the meeting of the Dutch-Flemish Society of the History of Economic Thought, 7 December 2001, Antwerp; at the 29th Meeting of the History of Economics Society, Davis CA, 5-8 July 2002; and at lunch seminars in Antwerp and Bristol. I would like to thank Christos Baloglou, Tony Brewer, Edmund Cannon, Annie Cot, Guido Erreygers, Charles Figuieres, Pat Gunning, Albert Jolink, Mary Morgan, Wilfried Parys, Renee Prendergast and Michael V.
    [Show full text]
  • Transcendental Numbers
    INTRODUCTION TO TRANSCENDENTAL NUMBERS VO THANH HUAN Abstract. The study of transcendental numbers has developed into an enriching theory and constitutes an important part of mathematics. This report aims to give a quick overview about the theory of transcen- dental numbers and some of its recent developments. The main focus is on the proof that e is transcendental. The Hilbert's seventh problem will also be introduced. 1. Introduction Transcendental number theory is a branch of number theory that concerns about the transcendence and algebraicity of numbers. Dated back to the time of Euler or even earlier, it has developed into an enriching theory with many applications in mathematics, especially in the area of Diophantine equations. Whether there is any transcendental number is not an easy question to answer. The discovery of the first transcendental number by Liouville in 1851 sparked up an interest in the field and began a new era in the theory of transcendental number. In 1873, Charles Hermite succeeded in proving that e is transcendental. And within a decade, Lindemann established the tran- scendence of π in 1882, which led to the impossibility of the ancient Greek problem of squaring the circle. The theory has progressed significantly in recent years, with answer to the Hilbert's seventh problem and the discov- ery of a nontrivial lower bound for linear forms of logarithms of algebraic numbers. Although in 1874, the work of Georg Cantor demonstrated the ubiquity of transcendental numbers (which is quite surprising), finding one or proving existing numbers are transcendental may be extremely hard. In this report, we will focus on the proof that e is transcendental.
    [Show full text]
  • BU-581-M.Pdf (1.982Mb)
    ADOLPHE QUETELI'r, P'ATUEB. OF UODERN STATISTICS! 'l'homas S. Graves BU-581-l'i lfay 1976 Abstract A brief history of statistics up untU 1820 is presented, along with a quick sketch of the clevel.Dpment of the normal distribution an4 the laws . of large numbers before 1820. 'lhen a biography of Adolphe QUetelet is given and it is shown how be combined the art of statistics with the theory of probabil'ity to form the science of statistics. His other contributions to statistics are also listed. Iiitrocluction 'l'he purpose of this paper is twofold. First a brief history of statis­ tics up to 1820 wUl be given, along with a quick sketch of the development of the laws of large numbers and the normal distribution. Secondly, a .JJ:,v; '· biography of Adolphe Quetelet with the emphasis on his achievements in sta- .. ; -~, . tistics will be presented. It will be shown how he canbiDed what was then called statistics with probability theory to develop what-we today call statistics. For this reason, Quetelet is often refel'red to as the father of modern statistics. He was also influential in the standardization of international statistics, helped to promote the use of statistical fJlethodol- ogy in other fields of science which rely upon observational data and laid the groundwork for modern sociology. He changed the role of the statistician . .. from that of artisan, gathering data and maltin& official tables to that of scien- tist1 seeking out the laws of nature. -2- ,_ .. ' Historx of Statistics , The practice of recording the numerical quantities which make up the state goes back to the very origins of recorded his tory.
    [Show full text]
  • Obal, D., Wadhwa, A. the Obesity Paradox
    The obesity paradox: does it exist in the perioperative period? Detlef Obal, MD, PhD, DESAa,b,c, Anupama Wadhwa, MBBS, MSc, FASAc,d At least 30% of the surgical population consists of patients who hypertension, and hyperlipidemia, and an increased risk of fulfill the definition of obesity, mirroring the obesity epidemic in thrombosis and inflammation, leading to higher mortality rates.7 – the general population in the United States.1 3 Nearly 74% of the However, neither BMI nor waist circumference reflects the participants in the American College of Surgeons National metabolic and inflammatory profiles of the patient. Therefore, a Surgical Quality Improvement Program (NSQIP) had an abnor- new definition of obesity was introduced emphasizing the term mally high body mass index (BMI), including 17% of patients adiposopathy and acknowledging individual body fat composi- younger than 18 years of age.4,5 This development is of particular tion and functionality.8 According to the definition of adiposo- concern as obesity is associated with an increased risk of meta- pathy, 4 different types of phenotypes are distinguished as bolic syndrome, hypertension, coronary artery disease (CAD), follows: and diabetes mellitus. However, physicians, nutritionists, and the (1) Normal weight obese (NWO). general public struggle with definitions of obesity based only on (2) Metabolically obese with normal weight (MONW). total body weight proportionate to height and, therefore, BMI. (3) Metabolically healthy obese (MHO). This leads to the question of whether BMI can adequately (4) Metabolically unhealthy obese (MUO) or “at risk” obese describe the physical condition of and potential risks in our patients suffering from complications directly related to patients.
    [Show full text]
  • Solving Recurrence Equations
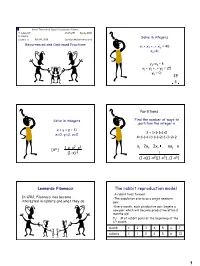
    Great Theoretical Ideas In Computer Science V. Adamchik CS 15-251 Spring 2010 D. Sleator Solve in integers Lecture 8 Feb 04, 2010 Carnegie Mellon University Recurrences and Continued Fractions x1 + x2 +…+ x5 = 40 xkrk; yk=xk – k y1 + y2 +…+ y5 = 25 y ≥ 0; k 29 4 Partitions Solve in integers Find the number of ways to partition the integer n x + y + z = 11 3 = 1+1+1=1+2 xr0; yb3; zr0 4=1+1+1+1=1+1+2=1+3=2+2 2 3 x1 2x2 3x3 ... nxn n [X11] 1 x x x (1 -x) 2 1 (1 -x)(1 -x2)(1 -x3)...(1 -xn) Leonardo Fibonacci The rabbit reproduction model •A rabbit lives forever In 1202, Fibonacci has become •The population starts as a single newborn interested in rabbits and what they do pair •Every month, each productive pair begets a new pair which will become productive after 2 months old Fn= # of rabbit pairs at the beginning of the nth month month 1 2 3 4 5 6 7 rabbits 1 1 2 3 5 8 13 1 F =0, F =1, 0 1 WARNING!!!! Fn=Fn-1+Fn-2 for n≥2 This lecture has What is a closed form explicit mathematical formula for Fn? content that can be shocking to some students. n n-1 n-2 Characteristic Equation - - = 0 n-2 2 Characteristic Fn=Fn-1+Fn-2 iff ( - - 1) = 0 equation Consider solutions of the form: iff 2 - - 1 = 0 n 1 5 Fn= for some (unknown) constant ≠ 0 2 = , or = -1/ must satisfy: (“phi”) is the golden ratio n - n-1 - n-2 = 0 a,b a n + b (-1/ )n = , or = -(1/ ) satisfies the inductive condition So for all these values of the Adjust a and b to fit the base inductive condition is satisfied: conditions.
    [Show full text]
  • Florence Nightingale and Oxford Statistics
    Florence Nightingale and Oxford Statistics Florence Nightingale’s influence on nursing is well known but her influence on the development and use of statistics is less familiar. Taught by her father, Florence Nightingale (1820–1910) showed a gift for mathematics from an early age, and studied the pioneering works on statistics by Adolphe Quetelet, one of the founders of the Royal Statistical Society (RSS). Florence Nightingale (1820–1910) & !e Royal Statistical Society "e RSS was founded in 1834 as the Statistical Society of London, and Florence Nightingale became its !rst female member in 1858. She used statistical methods to analyse the mortality and medical data she had collected while nursing during the Crimean War (1853–6) and was a pioneer in the visual presentation of information and statistical graphics. She is credited with developing a form of the pie chart now known as the polar area diagram. Benjamin Jowett (1817–1893) Aer returning as an invalid from the Crimean War, Florence Nightingale met the reforming Master of Balliol, Benjamin Jowett, and continued a long correspondence with him !e Department of Statistics until he died in 1893. In 1874 aer the death of Quetelet she suggested that ‘the only !tting Sadly Jowett’s plan came to nothing, memorial to Q’ would be to ‘introduce his although a highly distinguished statistician, science in the studies of Oxford’. "ough no Francis Edgeworth, held the post of Professor mathematician, Jowett believed strongly in the of Political Economy in Oxford from 1891 to use of statistics in medicine and developed 1922. Oxford’s !rst Professor of Statistics was a plan for their joint endowment, supplemented appointed in 1948 within Social Studies, and by ‘begging of the rich people of the world’, in 1988 the Department of Statistics was of a Professorship of Statistics at Oxford.
    [Show full text]
  • A Computable Absolutely Normal Liouville Number
    MATHEMATICS OF COMPUTATION Volume 84, Number 296, November 2015, Pages 2939–2952 http://dx.doi.org/10.1090/mcom/2964 Article electronically published on April 24, 2015 A COMPUTABLE ABSOLUTELY NORMAL LIOUVILLE NUMBER VERONICA´ BECHER, PABLO ARIEL HEIBER, AND THEODORE A. SLAMAN Abstract. We give an algorithm that computes an absolutely normal Liou- ville number. 1. The main result The set of Liouville numbers is {x ∈ R \ Q : ∀k ∈ N, ∃q ∈ N,q>1and||qx|| <q−k} where ||x|| =min{|x−m| : m ∈ Z} is the distance of a real number x to the nearest −k! integer and other notation is as usual. Liouville’s constant, k≥1 10 ,isthe standard example of a Liouville number. Though uncountable, the set of Liouville numbers is small, in fact, it is null, both in Lebesgue measure and in Hausdorff dimension (see [6]). We say that a base is an integer s greater than or equal to 2. A real number x is normal to base s if the sequence (sjx : j ≥ 0) is uniformly distributed in the unit interval modulo one. By Weyl’s Criterion [11], x is normal to base s if and only if certain harmonic sums associated with (sjx : j ≥ 0) grow slowly. Absolute normality is normality to every base. Bugeaud [6] established the existence of absolutely normal Liouville numbers by means of an almost-all argument for an appropriate measure due to Bluhm [3, 4]. The support of this measure is a perfect set, which we call Bluhm’s fractal, all of whose irrational elements are Liouville numbers.
    [Show full text]