DOCSLIB.ORG

Section 4.1 Linear Functions and Their Properties

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Section 4.1 Linear Functions and Their Properties Section 4.1 Linear Functions and Their Properties Linear Function A linear function is a function of the form , where is the slop and is y-intercept. ∆ Slope Average Rate of Change ∆ Only linear functions have a constant average rate of change. If a function has a constant average rate of change, the function is linear. If a function does not have a constant average rate of change, the function is nonlinear. Increasing, Decreasing and Constant A linear function is increasing, if . A linear function is decreasing, if . A linear function is constant, if . Exercises 1. (Solution 1) (a) g The slope y-intercept (b) Adjust “Window” 10, 10, 2 by 10, 10, 2 (c) average rate of change = slope (d) g 34 is increasing because the slope of the function is positive; 30 Cheon-Sig Lee www.coastalbend.edu/lee Page 1 Section 4.1 Linear Functions and Their Properties (Solution 2) 2. y-intercept 03 3 10 3 0 3 21 6 3 3 32 6 3 3 32 Because the rate of change, 3, is constant, the function is linear. ← 3, 3 33 Thus, the equation of the line is 33 (Solution 3) 3. 10 30 20 21 2 10 8 32 6 2 4 43 4 6 10 54 Because the rate of change is not constant, the function is nonlinear. 4. (Solution 4.a) 0 0 78 ← 0 8 8 8 8 7 ⇒ 7 (Solution 4.b) 0 7 8 0 8 8 8 7 8 ⇒ 7 8 Thus, the interval is ,∞. 7 Cheon-Sig Lee www.coastalbend.edu/lee Page 2 Section 4.1 Linear Functions and Their Properties 4. Continued… (Solution 4.c) g 7 8 5 4 5 5 12 8 4 8 8 12 12 1 (Solution 4.d) g 7 8 5 4 5 5 12 12 1 Thus, the interval is ∞, 1. (Solution 4.e) The Solution to the system of linear equations is the point of intercept. In (c) we have 1 for g. Because 1 71 81 and g 1 51 41, the intercept is 1, 1. 5. (Solution 5.a) is the cost for the given value of x in miles. 0.25 40 ← 120 120 0.25120 40 70 Therefore, the cost is $70 at 120 miles. (Solution 5.b) The given coast is $90 0.25 40 ← 90 90 0.25 40 40 40 50 0.25 50 0.25 (Solution 5.c) 0.25 0.25 80 200 0.25 40 80 Therefore, the person drove 200 miles with $90. 40 40 0.25 40 (Solution 5.d) 0.25 40 The cost is a function of x and the x is the number of 0.25 0.25 miles driven. Thus, the domain is the number of miles 160 driven. The number of miles driven cannot be negative. Thus, the person can drive 160 miles maximum. Therefore, the domain of is 0, ∞. Cheon-Sig Lee www.coastalbend.edu/lee Page 3 Section 4.1 Linear Functions and Their Properties 5. Continued… (Solution 5.e.f) The cost 0.25 40 is a linear function of x. Because 0.25 is the positive slope, the cost increases by 0.25. Because 40 is the y-intercept and is the cost for 0 mile driven, it is the minimum payment for renting the moving truck. 6. (Solution 6.a) Because a new computer is $3200, the value 0 3200. So, the first point is 0, 3200 that is the y-intercept. Because the value of the computer depreciate for 4 years, the value 4 0. So the second point is 4, 0. 0 3200 800 40 ← 800, 3200 800 3200 (Solution 6.b) Because the company chooses to depreciate for 4 years, the domain is 0, 4. (Solution 6.c) Plot two points obtained in (a) 0, 3200, 4, 0 (Solution 6.d) (Solution 6.d) 2, 1600 (Solution 6.e) 800 3200 ←2 3, 800 2 8002 3200 1600 (Solution 6.e) 800 3200 ← 800 800 800 3200 3200 3200 2400 800 ⇒3 Cheon-Sig Lee www.coastalbend.edu/lee Page 4 Section 4.1 Linear Functions and Their Properties 7. (Solution 7) Let be the cost for renting a truck and x be the number of miles driven. $26 is a fixed charge and the average rate of change is $0.10 for each mile driven. Then a linear equation for the cost is 0.10 26 If the truck is driven 151 miles, the cost is If the truck is driven 500 miles, the cost is 0.10 26 ← 151 0.10 26 ← 151 151 0.10151 26 500 0.10500 26 41.1 76 Cheon-Sig Lee www.coastalbend.edu/lee Page 5 .
Load more

Recommended publications
  • The Linear Algebra Version of the Chain Rule 1
    Ralph M Kaufmann The Linear Algebra Version of the Chain Rule 1 Idea The differential of a differentiable function at a point gives a good linear approximation of the function – by definition. This means that locally one can just regard linear functions. The algebra of linear functions is best described in terms of linear algebra, i.e. vectors and matrices. Now, in terms of matrices the concatenation of linear functions is the matrix product. Putting these observations together gives the formulation of the chain rule as the Theorem that the linearization of the concatenations of two functions at a point is given by the concatenation of the respective linearizations. Or in other words that matrix describing the linearization of the concatenation is the product of the two matrices describing the linearizations of the two functions. 1. Linear Maps Let V n be the space of n–dimensional vectors. 1.1. Definition. A linear map F : V n → V m is a rule that associates to each n–dimensional vector ~x = hx1, . xni an m–dimensional vector F (~x) = ~y = hy1, . , yni = hf1(~x),..., (fm(~x))i in such a way that: 1) For c ∈ R : F (c~x) = cF (~x) 2) For any two n–dimensional vectors ~x and ~x0: F (~x + ~x0) = F (~x) + F (~x0) If m = 1 such a map is called a linear function. Note that the component functions f1, . , fm are all linear functions. 1.2. Examples. 1) m=1, n=3: all linear functions are of the form y = ax1 + bx2 + cx3 for some a, b, c ∈ R.
    [Show full text]
  • Characterization of Non-Differentiable Points in a Function by Fractional Derivative of Jumarrie Type
    Characterization of non-differentiable points in a function by Fractional derivative of Jumarrie type Uttam Ghosh (1), Srijan Sengupta(2), Susmita Sarkar (2), Shantanu Das (3) (1): Department of Mathematics, Nabadwip Vidyasagar College, Nabadwip, Nadia, West Bengal, India; Email: [email protected] (2):Department of Applied Mathematics, Calcutta University, Kolkata, India Email: [email protected] (3)Scientist H+, RCSDS, BARC Mumbai India Senior Research Professor, Dept. of Physics, Jadavpur University Kolkata Adjunct Professor. DIAT-Pune Ex-UGC Visiting Fellow Dept. of Applied Mathematics, Calcutta University, Kolkata India Email (3): [email protected] The Birth of fractional calculus from the question raised in the year 1695 by Marquis de L'Hopital to Gottfried Wilhelm Leibniz, which sought the meaning of Leibniz's notation for the derivative of order N when N = 1/2. Leibnitz responses it is an apparent paradox from which one day useful consequences will be drown. Abstract There are many functions which are continuous everywhere but not differentiable at some points, like in physical systems of ECG, EEG plots, and cracks pattern and for several other phenomena. Using classical calculus those functions cannot be characterized-especially at the non- differentiable points. To characterize those functions the concept of Fractional Derivative is used. From the analysis it is established that though those functions are unreachable at the non- differentiable points, in classical sense but can be characterized using Fractional derivative. In this paper we demonstrate use of modified Riemann-Liouvelli derivative by Jumarrie to calculate the fractional derivatives of the non-differentiable points of a function, which may be one step to characterize and distinguish and compare several non-differentiable points in a system or across the systems.
    [Show full text]
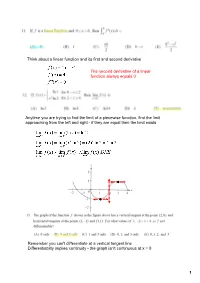
  • 1 Think About a Linear Function and Its First and Second Derivative The
    Think about a linear function and its first and second derivative The second derivative of a linear function always equals 0 Anytime you are trying to find the limit of a piecewise function, find the limit approaching from the left and right ­ if they are equal then the limit exists Remember you can't differentiate at a vertical tangent line Differentiabilty implies continuity ­ the graph isn't continuous at x = 0 1 To find the velocity, take the first derivative of the position function. To find where the velocity equals zero, set the first derivative equal to zero 2 From the graph, we know that f (1) = 0; Since the graph is increasing, we know that f '(1) is positive; since the graph is concave down, we know that f ''(1) is negative Possible points of inflection ­ need to set up a table to see where concavity changes (that verifies points of inflection) (­∞, ­1) (­1, 0) (0, 2) (2, ∞) + ­ + + concave up concave down concave up concave up Since the concavity changes when x = ­1 and when x = 0, they are points of inflection. x = 2 is not a point of inflection 3 We need to find the derivative, find the critical numbers and use them in the first derivative test to find where f (x) is increasing and decreasing (­∞, 0) (0, ∞) ­ + Decreasing Increasing 4 This is the graph of y = cos x, shifted right (A) and (C) are the only graphs of sin x, and (A) is the graph of ­sin x, which reflects across the x­axis 5 Take the derivative of the velocity function to find the acceleration function There are no critical numbers, because v '(t) doesn't ever equal zero (you can verify this by graphing v '(t) ­ there are no x­intercepts).
    [Show full text]
  • Algebra Vocabulary List (Definitions for Middle School Teachers)
    Algebra Vocabulary List (Definitions for Middle School Teachers) A Absolute Value Function – The absolute value of a real number x, x is ⎧ xifx≥ 0 x = ⎨ ⎩−<xifx 0 http://www.math.tamu.edu/~stecher/171/F02/absoluteValueFunction.pdf Algebra Lab Gear – a set of manipulatives that are designed to represent polynomial expressions. The set includes representations for positive/negative 1, 5, 25, x, 5x, y, 5y, xy, x2, y2, x3, y3, x2y, xy2. The manipulatives can be used to model addition, subtraction, multiplication, division, and factoring of polynomials. They can also be used to model how to solve linear equations. o For more info: http://www.stlcc.cc.mo.us/mcdocs/dept/math/homl/manip.htm http://www.awl.ca/school/math/mr/alg/ss/series/algsrtxt.html http://www.picciotto.org/math-ed/manipulatives/lab-gear.html Algebra Tiles – a set of manipulatives that are designed for modeling algebraic expressions visually. Each tile is a geometric model of a term. The set includes representations for positive/negative 1, x, and x2. The manipulatives can be used to model addition, subtraction, multiplication, division, and factoring of polynomials. They can also be used to model how to solve linear equations. o For more info: http://math.buffalostate.edu/~it/Materials/MatLinks/tilelinks.html http://plato.acadiau.ca/courses/educ/reid/Virtual-manipulatives/tiles/tiles.html Algebraic Expression – a number, variable, or combination of the two connected by some mathematical operation like addition, subtraction, multiplication, division, exponents and/or roots. o For more info: http://www.wtamu.edu/academic/anns/mps/math/mathlab/beg_algebra/beg_alg_tut11 _simp.htm http://www.math.com/school/subject2/lessons/S2U1L1DP.html Area Under the Curve – suppose the curve y=f(x) lies above the x axis for all x in [a, b].
    [Show full text]
  • Generic Continuous Functions and Other Strange Functions in Classical Real Analysis
    Georgia State University ScholarWorks @ Georgia State University Mathematics Theses Department of Mathematics and Statistics 4-17-2008 Generic Continuous Functions and other Strange Functions in Classical Real Analysis Douglas Albert Woolley Follow this and additional works at: https://scholarworks.gsu.edu/math_theses Part of the Mathematics Commons Recommended Citation Woolley, Douglas Albert, "Generic Continuous Functions and other Strange Functions in Classical Real Analysis." Thesis, Georgia State University, 2008. https://scholarworks.gsu.edu/math_theses/44 This Thesis is brought to you for free and open access by the Department of Mathematics and Statistics at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Mathematics Theses by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. GENERIC CONTINUOUS FUNCTIONS AND OTHER STRANGE FUNCTIONS IN CLASSICAL REAL ANALYSIS by Douglas A. Woolley Under the direction of Mihaly Bakonyi ABSTRACT In this paper we examine continuous functions which on the surface seem to defy well-known mathematical principles. Before describing these functions, we introduce the Baire Cate- gory theorem and the Cantor set, which are critical in describing some of the functions and counterexamples. We then describe generic continuous functions, which are nowhere differ- entiable and monotone on no interval, and we include an example of such a function. We then construct a more conceptually challenging function, one which is everywhere differen- tiable but monotone on no interval. We also examine the Cantor function, a nonconstant continuous function with a zero derivative almost everywhere. The final section deals with products of derivatives. INDEX WORDS: Baire, Cantor, Generic Functions, Nowhere Differentiable GENERIC CONTINUOUS FUNCTIONS AND OTHER STRANGE FUNCTIONS IN CLASSICAL REAL ANALYSIS by Douglas A.
    [Show full text]
  • Chapter 3. Linearization and Gradient Equation Fx(X, Y) = Fxx(X, Y)
    Oliver Knill, Harvard Summer School, 2010 An equation for an unknown function f(x, y) which involves partial derivatives with respect to at least two variables is called a partial differential equation. If only the derivative with respect to one variable appears, it is called an ordinary differential equation. Examples of partial differential equations are the wave equation fxx(x, y) = fyy(x, y) and the heat Chapter 3. Linearization and Gradient equation fx(x, y) = fxx(x, y). An other example is the Laplace equation fxx + fyy = 0 or the advection equation ft = fx. Paul Dirac once said: ”A great deal of my work is just playing with equations and see- Section 3.1: Partial derivatives and partial differential equations ing what they give. I don’t suppose that applies so much to other physicists; I think it’s a peculiarity of myself that I like to play about with equations, just looking for beautiful ∂ mathematical relations If f(x, y) is a function of two variables, then ∂x f(x, y) is defined as the derivative of the function which maybe don’t have any physical meaning at all. Sometimes g(x) = f(x, y), where y is considered a constant. It is called partial derivative of f with they do.” Dirac discovered a PDE describing the electron which is consistent both with quan- respect to x. The partial derivative with respect to y is defined similarly. tum theory and special relativity. This won him the Nobel Prize in 1933. Dirac’s equation could have two solutions, one for an electron with positive energy, and one for an electron with ∂ antiparticle One also uses the short hand notation fx(x, y)= ∂x f(x, y).
    [Show full text]
  • 1 Uniform Continuity
    Math 0450 Honors intro to analysis Spring, 2009 Notes 17 1 Uniform continuity Read rst: 5.4 Here are some examples of continuous functions, some of which we have done before. 1. A = (0; 1]; f : A R given by f (x) = 1 . ! x Proof. To prove that f is continuous at c (0; 1], suppose that " > 0, and 2 2 let = min c ; c " : If x c < , then rst of all, x > c and so 0 < 1 < 2 . 2 2 j j 2 x c Hence, n o 1 1 c x 1 1 2 1 c2" = = c x < = ": x c xc x c j j c c 2 2. f : R R given by f (x) = x2: ! Proof. Observe that x2 c2 = x c (x + c) : j j j j " If c = 0; let = p": If c = 0; let = min c ; 2 c If c = 0 and x c < , 6 j j j j j j then x < p" and x2 c2 = x2 < ", Ifnc = 0; theno j j j j j j 6 " x2 c2 = x + c x c < 2 c = ": j j j j j j 2 c j j 3. A = [1; ); f (x) = 1 . 1 x Proof. This makes use of item 1 above. Suppose that c A. From item 1, 2 2 we see that if " > 0, and x c < min c ; c " , then 1 1 < ". Hence, j j 2 2 x c 2 let = " : If x c < , and x and c aren in A, theno x c < min c ; c " ; so 2 j j j j 2 2 1 1 < ": n o x c 1 1 4.
    [Show full text]
  • Section 14.4 Tangent Planes and Linear Approximations
    Section 14.4 Tangent planes and linear approximations. Tangent planes. • Suppose a surface S has equation z = f(x, y), where f has continuous first partial derivatives, and let P (x0,y0,z0) be a point on S. • Let C1 and C2 be the curves obtained by intersecting the vertical planes y = y0 and x = x0 with the surface S. P lies on both C1 and C2. • Let T1 and T2 be the tangent lines to the curves C1 and C2 at the point P . • The tangent plane to the surface S at the point P is defined to be the plane that containts both of the tangent lines T1 and T2. An equation on the tangent plane to the surface z = f(x, y) at the point P (x0,y0,z0) is z − z0 = fx(x0,y0)(x − x0)+ fy(x0,y0)(y − y0) Example 1. Find the equation of the tangent plane to the surface z = ln(2x + y) at the point (−1, 3, 0). 1 Linear Approximations. An equation of a tangent plane to the graph of the function f of two variables at the point (a,b,f(a,b)) is z = f(a,b)+ fx(a,b)(x − a)+ fy(a,b)(y − b) The linear function L(x, y)= f(a,b)+ fx(a,b)(x − a)+ fy(a,b)(y − b) is called the linearization of f(a,b) and the approximation f(x, y) ≈ f(a,b)+ fx(a,b)(x − a)+ fy(a,b)(y − b) is called the linear approximation ot the tangent line approximation of f at (a,b).
    [Show full text]
  • Multivariate Approximation and Matrix Calculus
    Multivariate Approximation and Matrix Calculus Introduction Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. Any finite number of initial terms of the Taylor series of a function is called a Taylor polynomial. In single variable calculus, Taylor polynomial of n degrees is used to approximate an (n+1)-order differentiable function and the error of the approximation can be estimated by the (n+1)-th term of the Taylor series. By introducing vector and matrix calculus notations, we can express the same idea for multivariate functions and vector functions. Applications Because all numbers that can be represented by finite digits are rational numbers, the numerical computation of an irrational function at a particular point is almost always approximated. The first order and second order of Taylor polynomials are most frequently selected as the proper rational function to approximate irrational functions. This idea is called linear and quadratic approximation in calculus, respectively. In addition, the quadratic approximation is also used to in optimization because local maximum or minimum occurs at the critical points where the second term (first derivatives) of the Taylor polynomial is zero and the third term (second derivatives) are definitely positive or negative. In order to obtain the first or second order Taylor polynomial, we compute the coefficients of Taylor series by calculating the first and second derivatives of the original function. When we move towards the advanced mathematical applications (temperature in 4 dimensional temporal-spatial space and vector field of moving hurricane centers), we need to use multivariate (vector) functions, instead of single variable functions.
    [Show full text]
  • Convergent Factorial Series Solutions of Linear Difference Equations*
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF DIFFERENTIAL EQUATIONS 29, 345-361 (1978) Convergent Factorial Series Solutions of Linear Difference Equations* W. J. FITZPATRICK+ AND L. J. GRIMM Depal-tment of Mathematics, University of Missowi-Rolla, Rolh, Missotwi 65801 Received July 27, 1977 1. IPU’TRODUCTION Although the analytic theory of linear difference equations dates back to an 1885 memoir of Poincare, continuing work essentially began around 1910 with publication of several papers of G. D. Birkhoff, R. D. Carmichael, J. Horn, and N. E. Norlund; see, for instance, [l, 2, 4, 51. Since that time, C. R. Adams, M7. J. Trjitzinsky, and others have carried on the development of the theory; numerous contributions have been made in recent years by TV. A. Harris, Jr., P. Sibuya, and H. L. Turrittin; see, for instance, [7-9, 16-171. The monographs of Norlund [14] and L. M. Milne-Thomson [13] give a comprehensive account of earlier work, and references to more recent literature are given in the surrey paper of Harris [S]. The similarity between difference equations and differential equations has been noted by many investigators; for instance, Birkhoff [3] pointed out that the analytic theory of linear difference equations provides a “methodological pattern” for the “essentially simpler but analogous” theory of linear differential equations. In this paper, we apply a projection method which has been useful in the treat- ment of analytic differential equations [6, 101 to obtain existence theorems for convergent factorial series solutions of analytic difference equations.
    [Show full text]
  • Gradients Math 131 Multivariate Calculus D Joyce, Spring 2014
    Gradients Math 131 Multivariate Calculus D Joyce, Spring 2014 @f Last time. Introduced partial derivatives like @x of scalar-valued functions Rn ! R, also called scalar fields on Rn. Total derivatives. We've seen what partial derivatives of scalar-valued functions f : Rn ! R are and what they mean geometrically. But if these are only partial derivatives, then what is the `total' derivative? The answer will be, more or less, that the partial derivatives, taken together, form the to- tal derivative. Figure 1: A Lyre of Ur First, we'll develop the concept of total derivative for a scalar-valued function f : R2 ! R, that is, a scalar field on the plane R2. We'll find that that them. In that sense, the pair of these two slopes total derivative is what we'll call the gradient of will do what we want the `slope' of the plane to be. f, denoted rf. Next, we'll slightly generalize that We'll call the vector whose coordinates are these to a scalar-valued function f : Rn ! R defined partial derivatives the gradient of f, denoted rf, on n-space Rn. Finally we'll generalize that to a or gradf. vector-valued function f : Rn ! Rm. The symbol r is a nabla, and is pronounced \del" even though it's an upside down delta. The The gradient of a function R2 ! R. Let f be word nabla is a variant of nevel or nebel, an an- a function R2 ! R. The graph of this function, cient harp or lyre. One is shown in figure 1.
    [Show full text]
  • Sections 3.2: Recurrence Relations
    Sections 3.2: Recurrence Relations February 8, 2021 Abstract Recurrence relations are defined recursively, and solutions can sometimes be given in “closed-form” (that is, without re- course to the recursive definition). We will solve one type of linear recurrence relation to give a general closed-form solution, the solution being verified by induction. We’ll be getting some practice with summation notation in this section. Have you seen it before? 1 Solving Recurrence Relations Vocabulary: • linear recurrence relation: S(n) depends linearly on previous S(r), r<n: S(n)= f1(n)S(n − 1) + ··· + fk(n)S(n − k)+ g(n) That means no powers on S(r), or any other functions operat- ing on S(r). The relation is called homogeneous if g(n) = 0. (Both Fibonacci and factorial are examples of homogeneous linear recurrence relations.) • first-order: S(n) depends only on S(n − 1), and not previous terms. (Factorial is first-order, while Fibonacci is second-order, depending on the two previous terms.) • constant coefficient: In the linear recurrence relation, when the coefficients of previous terms are constants. (Fibonacci is constant coefficient; factorial is not.) • closed-form solution: S(n) is given by a formula which is sim- ply a function of n, rather than a recursive definition of itself. (Both Fibonacci and factorial have closed-form solutions.) The author suggests an “expand, guess, verify” method for solving recurrence relations. Example: The story of T (a) Practice 1, p. 159 (from the previous section): T (1) = 1 T (n)= T (n − 1)+3, for n ≥ 2 (b) Practice 9, p.
    [Show full text]