DOCSLIB.ORG

9 Serangoon Garden 20L7 Sa2 1.0 Sa2 LL S:A2 L2 ,Saz

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
9 Serangoon Garden 20L7 Sa2 1.0 Sa2 LL S:A2 L2 ,Saz Free Tuition Listing @ 99Tutors.SG $2s 1 sA2 2 sA2 3 sAL 4 sA2 5 sAL 5 ,sAL 7 sA2 8 sA2 9 Serangoon Garden 20L7 sA2 1.0 sA2 LL S:A2 L2 ,sAz 99Tutors.SG | Page 1 Free Tuition Listing @ 99Tutors.SG 99Tutors.SG | Page 2 BP/2017 13 Free Tuition Listing @ 99Tutors.SG tuUlo€lttttoe Sdroo, tMel, Rrmd) 2017 4EAM ACS (Barker Road) Prelim Asswer ail the questions t The equation uf a cuwe is y - 2x2 -6x+ k, whete kis a constaut' which y < 0 (D tn the case whep ,t = -20, find tre set of values of r for ' tzl thecurve' (ii) lnthecasewheu k =tO,show thattheline y +2x-8 isa tangentto FI in u' 2 $ Given thar u = i', express 4' -2'd = 3 as an equation t2l places' (ii) Hence {ind the iralue of x, oorcct to 2 decimal t3l < t21 (iii) Explain why the oquation 4' -2n1 = /c has no solution if & -l ' 3 Thecquation 3r2 'If5=0 hasrcotsGandP' (r) Find the valu€ of a' + Pt ' tsl t3I 2cos2 r' I - sin {cosr+ r as A quadraflcnuedt ' expresrsion in cot x. 4 (i) Express -:---H:F-::":: asa t3l sin x(3sin.r + cos r) (ii) Heuce, usiilg G) polve the equation I + 2cos2 x = for 0' < x< 360?. t4I r*{ ,Sec 4 (FqPressJ minali sn 20t 7 PtelirnirurY fu Additla*d nmrtler,tattcs 4047 PaWr 7 99Tutors.SG | Page 3 Free Tuition Listing @ 99Tutors.SG BPt2017 t4 Angrto-Cfn'nese Scfioal (@t@ Road) A fteshly baked bread, wirh an inicial rempem&re of 75'C, is lefi to cool orr the raek. The temperatrrre, io'C of the bread r rrinrtes after it has been placed on the rack is gtveri by ? =27 + lce-"', wher€ k atd. n are positive consEuts. [} Calculate the value of /r. trl (ii) If thebread has cooled doua by20'c after r0 minuteq find the value ofa- Lzl (iii) Find the least tirne takcn, to rhe nearesf minutg for the bread to have a tanperature of less than30'C. t3l (iv) Explain with the skech for f = 27 + lce-"', why tlre temperarure of the bread can nsv€f, reach 27'C, trI 4Ji -z'.li arrgle BAD = 30". Given that the leagth of AD is twice th€ i€ngth ot BC and that ' area of the trapezium [s 25 +sJE- cmz, find withoutthe use of a calculator, the Iengthof lD in the fonn 15 . "^fZ*t t4l part The diagmm shows of a straight line, passing through (2, r) and (8, 1 3) , drawn ro f@reseot the equation 3y = 4x' + at, whiere a and , arc conshnts. Find tlre ralue of a and t. (s, t3) t41 4 freli ml n ary fxaminalion Nl 7 I I 99Tutors.SG | Page 4 AtiditiondtLr,{rre*rr"*ini'!rtr'1, I I BP12017 15 Free Tuition Listing @ 99Tutors.SG Attg{o.Chlnese Scltool (B sks Roadl I ta) Given that the first 3 tetms in the expansion of (a - rxl + 3x)tr in ascending powers of x is 2+29x+ Df +..- Find the values of the constals a, b a*d n. tsI (b) O Writedopn the ge,neral termin the binomial exparsion of 1rt .' -l1ro2f' t1I (ii) Write down the power of x in this general term, trI (iii) Hence, ot otherwise, detetmine the coefficie,nt of x-ts in ttre binomial expansioir of (x2 * *. # t2l 9 A cune has equationyl rn( ,n" normal to the curue at the point (a, D) is ' i \5*2rll+;! ). paraltit'to the line lty uSx-25 = 0. Given that where a) l,find the values of a and D. tsl 10 The diagrarn shows pafilof the graph of y =lzx+ 4l + 1 . I -lz** 4l + I (i) FiaiC the coordinafes of P and of Q- t3l A Iine of gradiant a passes through the point (0,3). (ii) tn the case where ;m = -1, find the x-coordinates of the points of interscction be*ween the lineai:dtteeraph of y: l2.r+ al+l t3I (iii) Detennine the set bf vatues ofzz for which the line intersects the graph of y =px+al+ I at two points. sa Wirninary Breffiffiatton ZAfi I Affiiorral rt@rarnaries &47 fumy'i 99Tutors.SG | Page 5 I I BPt2017 t6 Free Tuition Listing @ 99Tutors.SG Angl o - Chl ne s e Sfim,l (U*q Roadl Il Aparticle stafts from rest and moves in asbaight line, so that t seconds afler leaving O, its velocity,vmlsis given by u= 23-ZeT . (D Calculate ttre initial accelerationof theparticle. t2l (ii) Calculate, to 2 decimal places, the displacanent of the particle from O when /= 10. t4l (iiD Ddennine, withexplanation, whether theparticlewill retrrn to O. lrI 12 In the diagrambelow, the line AE is tangeat to &e circle at 14. The line EB is the angle bisector of angle,{dC and cuts the cirple at D- The chord .4C is the argle bisector of anfie BAD and cuts thecirple at C. The chords BC arrd AD ate produced to meet at F. The line segments AD and FD xe e+El. (r) Prove fiat angle DAC: angle DAE, t3l (ii) Prove that trianglex- ADg and BAE are similar. l2l (iii) Prove that C is a mid-point of BF. t2l (ir) Hence, using (ii) and (iifl, show that AF x AE = 4CD x DE . V1 toellminq &wriration ZA't 7 .9ec 4 (Express/ 99Tutors.SG | Page 6 Additiortal tufeithernaties 4Ul F'aW t Free Tuition Listing @ 99Tutors.SG Ansrrer aII the questions (s] [ Given that lg0y + 2) - 4xL - /, exprffis y in terms of x. t3l (b) Soirr theequatioa Zlogn(8- 2*\- log:(r- Z)=3-Ioge(r+ x) IsI The diagriam shows 6r wtter wheel whichrotates at 3 revolutious per minute in au anticloc}s,ise dircctibnAt *re start of dre revolution, a poiut P on the rim of &e wheel is at the heiglrt of 3 rh above the strdace of the water. The radius of the water wheel is 4 trt" The height, ft m, of poiut P above the water surface is given I h = dsi(l}+c , wherel is thetime iri seconds. (i) Sute tre valugs ofs,&and c. t3l G) Fiod the time;f, whercpoint P first emage ftom the water. l3I show u* ti) ft{"*(2r+II=gk(4r+4}. IZT Cu) Hence, o, oth|*ir, evaluate a*. llz*u [4] On*$gwy Uarninelton 2A t 7 Se6 A{*ger} e&tltupll Wt{rcsnatics PaW ? 4047 99Tutors.SG | Page 7 BPt2017 t8 Free Tuition Listing @ 99Tutors.SG AtE,bl0hircce School (Aar*er Roadl The cubic polynomial (x) is such *rat tbe coefficient of.t' is 4 anil the constant ternr is -3. Whea rt I is a fictor of (r), the qrndratic factor is pi + qx+ r. tt is given that (,r) Ieaves a rclmailrder of -2O when divided by r - I . (r) Ffud dre values of P, q and r. t3] (ir} Solve (x):0. t2l Gii) Hence solve the equation (-r) = Q. tll \' : \1 - 4x +t It is given that x'-4 G) Findthe values of a,b and c. t3l (ii) Hencg using partiat ftactions and the values of a,h and c obtained in part (i), x3 _x:a|+t** find f t6l (r) ;'If,fu g sufves constants, 1i; Findthe value of a and of k. "127 (ii) On the same axes, sketch the two cutYes, for x > 0. tzl (2*+ wtren *= 8re value ' (b) Giveothaty= hnr)zand*fr., S -uE+DJ5 ;,find of a and of D. 141 dl loa 1 Sec 4 [E4press) P relblrii raty Erraitl rrat fr 7 I I Additiorral tielhettettcs P apet 2 4847 99Tutors.SG | Page 8 I I BP/2017 19 Free Tuition Listing @ 99Tutors.SG Anglo.Chtnese Scftoo/ (turlrcr Road) A curvehas the equation jr = f(r),where f(x) = 1'x-1) for x > 0. 5x+ 3 (i) Find an expression for f'(.r). t2l (if, Explain why thelcurve hes no sbtionary points. tu (iiil Show with full urprkings, deternaine whether tlre gradient function of the curve is ar incrcasing or decreasing function for r > 0. Th6 pornts (I, 10) and (?, l0) are on the circumference of a circle whose centr€i G lies above'tlre x-axis, The liue y = I is tangent to the circle. ' (i) F.inil the coordinates of C. t3l (ii) Find theeguatioriof thecirclein theform x'+ y' + px+W+ r =0, wtwe p,q and rareinteger$. (iii) ffud the quatiois of the hngeuE b the circle parallel to they-axis. tI The abovediagram sbonrs a troughof 3m long and lm deep with ABCD horizontal. Its cross section is an isosdeles triangle of base 2m with its vstex downwards. The empty trough is filleil with water at the rate of 0.03 m3/s. (D #ti" A"pttt of th$water at time ! seeonds is tr m, show that the volume of water is 3lr2 m3. ttI Gi) Henoe, find the rdte at which the water leivel is rising after the water has been runningfor25s. I4l rLa *t Frcffnlrnry &arnreitian fl? 7 Sac 0 {furesel Addifurlelt eraffu,?Baf,bs tuW 2 4847 99Tutors.SG | Page 9 Free Tuition Listing @ 99Tutors.SG BPt2017t10 ArpltChiaese Sclrool (8erker Road) IO !:rr-3 The diagram shows part of the curve ard two pmallet lines Or? arfr. PQ. The line OR interseots the curue at the poiut ,R (2,2) aod the lirte PQ is a tangent to the curveatthe poir,t O. O Fiud thecoordinatcs of P and of Q. t4I (ii) Find the atez:.of thesbadd region OPOR t6l (i) Find the coordioates af B arr.d D.
Load more

Recommended publications
  • Highline Residences Understand Your Credit Report Property Markettrends 2015 Designer
    (w/GST) S$5.80 PRICE: Apr 2015 Apr - Mar Singapore Property Singapore Property International Property Highline Residences Understand Your Credit Report Credit Understand Your Property Market Trends 2015 MarketTrends Property Designer A Property ThatGoesAboveAndBeyond A Property Homes Crowdfunders Magazine Con t e n t s SINGAPORE PROPERTY ANALYSIS 4 Property Market Trends for 2015 6 SRX Residential Property Flash Report (Feb 2015) 9 SRX Residential Property Flash Report (Jan 2015) 11 SRX Residential Property Flash Report (Rental Market) PROPERTY SPOTLIGHT 12 SEA’s First Real Estate Crowdfunding Site CoAssets’ seals S$1 million investment – CoAssets FINANCE 13 Understanding Your Credit Report by Credit Bureau PROPERTY SHOWCASE 20 14 A property that goesAbove and Beyond – Highline Residences 16 A New Level of Inclusiveness – Sims Urban Oasis 18 The New Treasure in Jurong Lake District – Lakeville 20 The Gem of the East – Meridian 38 22 Crown At Robinson INTERNATIONAL PROPERTY ANALYSIS 52 Penang Real Estate Market – Henry Butcher Malaysia Sdn Bhd PROPERTY SHOWCASE 50 Bridging Possibilities In Phnom Penh – The Bridge 22 EVENT 62 Piscine SPLASH! Asia DESIGNER HOMES returns to Singapore and announces new show features 64 Adventure Home - Rezt & Relax Interior 70 Art Party - I-Bridge Design Pte Ltd 74 to Back Cover CROWDFUNDERS Magazine HOMEBUYERS: MCI(P)131/11/2014. ISSN 0129 - 8703 is published Bi-monthly available at bookstores & newstands at S$5.80 (w/GST). Publisher: PROPERTY MEDIA, 808 French Road #07-163 Kitchener Complex Singapore 200808. Tel: (65) 6294 4588 Fax: (65) 6294 5812. Email: [email protected]. (This issue of Homebuyers come with Crowdfunders magazine).
    [Show full text]
  • Participating Merchants
    PARTICIPATING MERCHANTS PARTICIPATING POSTAL ADDRESS MERCHANTS CODE 460 ALEXANDRA ROAD, #01-17 AND #01-20 119963 53 ANG MO KIO AVENUE 3, #01-40 AMK HUB 569933 241/243 VICTORIA STREET, BUGIS VILLAGE 188030 BUKIT PANJANG PLAZA, #01-28 1 JELEBU ROAD 677743 175 BENCOOLEN STREET, #01-01 BURLINGTON SQUARE 189649 THE CENTRAL 6 EU TONG SEN STREET, #01-23 TO 26 059817 2 CHANGI BUSINESS PARK AVENUE 1, #01-05 486015 1 SENG KANG SQUARE, #B1-14/14A COMPASS ONE 545078 FAIRPRICE HUB 1 JOO KOON CIRCLE, #01-51 629117 FUCHUN COMMUNITY CLUB, #01-01 NO 1 WOODLANDS STREET 31 738581 11 BEDOK NORTH STREET 1, #01-33 469662 4 HILLVIEW RISE, #01-06 #01-07 HILLV2 667979 INCOME AT RAFFLES 16 COLLYER QUAY, #01-01/02 049318 2 JURONG EAST STREET 21, #01-51 609601 50 JURONG GATEWAY ROAD JEM, #B1-02 608549 78 AIRPORT BOULEVARD, #B2-235-236 JEWEL CHANGI AIRPORT 819666 63 JURONG WEST CENTRAL 3, #B1-54/55 JURONG POINT SHOPPING CENTRE 648331 KALLANG LEISURE PARK 5 STADIUM WALK, #01-43 397693 216 ANG MO KIO AVE 4, #01-01 569897 1 LOWER KENT RIDGE ROAD, #03-11 ONE KENT RIDGE 119082 BLK 809 FRENCH ROAD, #01-31 KITCHENER COMPLEX 200809 Burger King BLK 258 PASIR RIS STREET 21, #01-23 510258 8A MARINA BOULEVARD, #B2-03 MARINA BAY LINK MALL 018984 BLK 4 WOODLANDS STREET 12, #02-01 738623 23 SERANGOON CENTRAL NEX, #B1-30/31 556083 80 MARINE PARADE ROAD, #01-11 PARKWAY PARADE 449269 120 PASIR RIS CENTRAL, #01-11 PASIR RIS SPORTS CENTRE 519640 60 PAYA LEBAR ROAD, #01-40/41/42/43 409051 PLAZA SINGAPURA 68 ORCHARD ROAD, #B1-11 238839 33 SENGKANG WEST AVENUE, #01-09/10/11/12/13/14 THE
    [Show full text]
  • List-Of-Bin-Locations-1-1.Pdf
    List of publicly accessible locations where E-Bins are deployed* *This is a working list, more locations will be added every week* Name Location Type of Bin Placed Ace The Place CC • 120 Woodlands Ave 1 3-in-1 Bin (ICT, Bulb, Battery) Apple • 2 Bayfront Avenue, B2-06, MBS • 270 Orchard Rd Battery and Bulb Bin • 78 Airport Blvd, Jewel Airport Ang Mo Kio CC • Ang Mo Kio Avenue 1 3-in-1 Bin (ICT, Bulb, Battery) Best Denki • 1 Harbourfront Walk, Vivocity, #2-07 • 3155 Commonwealth Avenue West, The Clementi Mall, #04- 46/47/48/49 • 68 Orchard Road, Plaza Singapura, #3-39 • 2 Jurong East Street 21, IMM, #3-33 • 63 Jurong West Central 3, Jurong Point, #B1-92 • 109 North Bridge Road, Funan, #3-16 3-in-1 Bin • 1 Kim Seng Promenade, Great World City, #07-01 (ICT, Bulb, Battery) • 391A Orchard Road, Ngee Ann City Tower A • 9 Bishan Place, Junction 8 Shopping Centre, #03-02 • 17 Petir Road, Hillion Mall, #B1-65 • 83 Punggol Central, Waterway Point • 311 New Upper Changi Road, Bedok Mall • 80 Marine Parade Road #03 - 29 / 30 Parkway Parade Complex Bugis Junction • 230 Victoria Street 3-in-1 Bin Towers (ICT, Bulb, Battery) Bukit Merah CC • 4000 Jalan Bukit Merah 3-in-1 Bin (ICT, Bulb, Battery) Bukit Panjang CC • 8 Pending Rd 3-in-1 Bin (ICT, Bulb, Battery) Bukit Timah Plaza • 1 Jalan Anak Bukit 3-in-1 Bin (ICT, Bulb, Battery) Cash Converters • 135 Jurong Gateway Road • 510 Tampines Central 1 3-in-1 Bin • Lor 4 Toa Payoh, Blk 192, #01-674 (ICT, Bulb, Battery) • Ang Mo Kio Ave 8, Blk 710A, #01-2625 Causeway Point • 1 Woodlands Square 3-in-1 Bin (ICT,
    [Show full text]
  • Participating Merchants Address Postal Code Club21 3.1 Phillip Lim 581 Orchard Road, Hilton Hotel 238883 A|X Armani Exchange
    Participating Merchants Address Postal Code Club21 3.1 Phillip Lim 581 Orchard Road, Hilton Hotel 238883 A|X Armani Exchange 2 Orchard Turn, B1-03 ION Orchard 238801 391 Orchard Road, #B1-03/04 Ngee Ann City 238872 290 Orchard Rd, 02-13/14-16 Paragon #02-17/19 238859 2 Bayfront Avenue, B2-15/16/16A The Shoppes at Marina Bay Sands 018972 Armani Junior 2 Bayfront Avenue, B1-62 018972 Bao Bao Issey Miyake 2 Orchard Turn, ION Orchard #03-24 238801 Bonpoint 583 Orchard Road, #02-11/12/13 Forum The Shopping Mall 238884 2 Bayfront Avenue, B1-61 018972 CK Calvin Klein 2 Orchard Turn, 03-09 ION Orchard 238801 290 Orchard Road, 02-33/34 Paragon 238859 2 Bayfront Avenue, 01-17A 018972 Club21 581 Orchard Road, Hilton Hotel 238883 Club21 Men 581 Orchard Road, Hilton Hotel 238883 Club21 X Play Comme 2 Bayfront Avenue, #B1-68 The Shoppes At Marina Bay Sands 018972 Des Garscons 2 Orchard Turn, #03-10 ION Orchard 238801 Comme Des Garcons 6B Orange Grove Road, Level 1 Como House 258332 Pocket Commes des Garcons 581 Orchard Road, Hilton Hotel 238883 DKNY 290 Orchard Rd, 02-43 Paragon 238859 2 Orchard Turn, B1-03 ION Orchard 238801 Dries Van Noten 581 Orchard Road, Hilton Hotel 238883 Emporio Armani 290 Orchard Road, 01-23/24 Paragon 238859 2 Bayfront Avenue, 01-16 The Shoppes at Marina Bay Sands 018972 Giorgio Armani 2 Bayfront Avenue, B1-76/77 The Shoppes at Marina Bay Sands 018972 581 Orchard Road, Hilton Hotel 238883 Issey Miyake 581 Orchard Road, Hilton Hotel 238883 Marni 581 Orchard Road, Hilton Hotel 238883 Mulberry 2 Bayfront Avenue, 01-41/42 018972
    [Show full text]
  • 136 Bus Time Schedule & Line Route
    136 bus time schedule & line map 136 Ang Mo Kio Int View In Website Mode The 136 bus line (Ang Mo Kio Int) has 2 routes. For regular weekdays, their operation hours are: (1) Ang Mo Kio Int: 5:45 AM - 11:43 PM (2) Punggol Temp Int: 5:45 AM - 11:24 PM Use the Moovit App to ƒnd the closest 136 bus station near you and ƒnd out when is the next 136 bus arriving. Direction: Ang Mo Kio Int 136 bus Time Schedule 41 stops Ang Mo Kio Int Route Timetable: VIEW LINE SCHEDULE Sunday 6:00 AM - 11:44 PM Monday 5:45 AM - 11:43 PM Punggol Pl - Punggol Temp Int (65009) 70A Punggol Place, Singapore Tuesday 5:45 AM - 11:43 PM Punggol Ctrl - Blk 303d (65221) Wednesday 5:45 AM - 11:43 PM 303D Punggol Place, Singapore Thursday 5:45 AM - 11:43 PM Punggol Ctrl - Punggol Sec/Blk 601b (65281) Friday 5:45 AM - 11:43 PM 601B Punggol Central, Singapore Saturday 5:45 AM - 11:43 PM Edgeƒeld Plains - Blk 178 (65249) 178 Edgeƒeld Plains, Singapore Punggol Field - Cove Stn Exit A (65159) 50 Punggol Field, Singapore 136 bus Info Direction: Ang Mo Kio Int Punggol Rd - Blk 102c (65079) Stops: 41 102C Punggol Field, Singapore Trip Duration: 65 min Line Summary: Punggol Pl - Punggol Temp Int Punggol Rd - Blk 190c (65069) (65009), Punggol Ctrl - Blk 303d (65221), Punggol Punggol Road, Singapore Ctrl - Punggol Sec/Blk 601b (65281), Edgeƒeld Plains - Blk 178 (65249), Punggol Field - Cove Stn Exit A Punggol Rd - St.
    [Show full text]
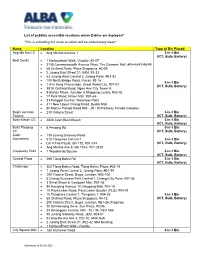
  • List of Publicly Accessible Locations Where E-Bins Are Deployed*
    List of publicly accessible locations where E-Bins are deployed* *This is a working list, more locations will be added every week* Name Location Type of Bin Placed Ang Mo Kio CC • Ang Mo Kio Avenue 1 3-in-1 Bin (ICT, Bulb, Battery) Best Denki • 1 Harbourfront Walk, Vivocity, #2-07 • 3155 Commonwealth Avenue West, The Clementi Mall, #04-46/47/48/49 • 68 Orchard Road, Plaza Singapura, #3-39 • 2 Jurong East Street 21, IMM, #3-33 • 63 Jurong West Central 3, Jurong Point, #B1-92 • 109 North Bridge Road, Funan, #3-16 3-in-1 Bin • 1 Kim Seng Promenade, Great World City, #07-01 (ICT, Bulb, Battery) • 391A Orchard Road, Ngee Ann City Tower A • 9 Bishan Place, Junction 8 Shopping Centre, #03-02 • 17 Petir Road, Hillion Mall, #B1-65 • 83 Punggol Central, Waterway Point • 311 New Upper Changi Road, Bedok Mall • 80 Marine Parade Road #03 - 29 / 30 Parkway Parade Complex Bugis Junction • 230 Victoria Street 3-in-1 Bin Towers (ICT, Bulb, Battery) Bukit Merah CC • 4000 Jalan Bukit Merah 3-in-1 Bin (ICT, Bulb, Battery) Bukit Panjang • 8 Pending Rd 3-in-1 Bin CC (ICT, Bulb, Battery) Cash • 135 Jurong Gateway Road Converters • 510 Tampines Central 1 3-in-1 Bin • Lor 4 Toa Payoh, Blk 192, #01-674 (ICT, Bulb, Battery) • Ang Mo Kio Ave 8, Blk 710A, #01-2625 Causeway Point • 1 Woodlands Square 3-in-1 Bin (ICT, Bulb, Battery) Central Plaza • 298 Tiong Bahru Rd 3-in-1 Bin (ICT, Bulb, Battery) Challenger • 302 Tiong Bahru Road, Tiong Bahru Plaza, #03-19 • 1 Jurong West Central 2, Jurong Point, #B1-94 • 200 Victoria Street, Bugis Junction, #03-10E • 5 Changi Business
    [Show full text]
  • Bank & Branch Code Guide
    ACH BANK & BRANCH CODE GUIDEs Last updated: 20 September 2021 IMPORTANT NOTE: 1. This guide is for customer using the old IBG payment and collections. 2. Customer using the new FAST/GIRO service, please be reminded that the following 3 banks require the 3 digits branch code to be appended to the account number. OCBC – Oversea-Chinese Banking Corporation Limited HSBC – The Hongkong & Shanghai Banking Corporation Limited SBI – State Bank of India Please follow the instruction given in Appendix C for more information. 3. UOB will not be held responsible for any errors or omissions that may appear in the guide. For updates of the codes, please refer to www.uobgroup.com/ACHcodes. 4. For DBS enquiries, please call 1800 222 2200. For OCBC enquiries, please call 1800 438 3333. The ACH Bank Code, Branch Code and Account Number are key fields in the required information to be provided for Interbank GIRO (IBG) transactions only. For accounts belonging to the following banks, you may wish to take note of the following conditions when preparing the IBG transactions: Bank Bank Branch Account Remarks Name Code Code No (Example) - 10-digit Account No - Use first 3 digits of Account No and refer to Appendix A to retrieve the corresponding Branch Code UOB 7375 030 9102031012 eg. For account 9102031012, use 910 to refer to Appendix A to retrieve the Branch Code 030. (Account No will remain as 9102031012.) UOB 7375 001 860012349101 - VAN: Virtual Account Number (for VAN - Length of Account Number varies from 7 to account 18 digits (except 8, 10, 15 and 16) only) - Use 001 as default Branch Code - Usually 10-digit Account No - Use first 3 digits of Account No as the Branch Code DBS 7171 005 0052312891 eg.
    [Show full text]
  • Ministry of Health List of Approved Offsite Providers for Polymerase Chain Reaction (PCR) Tests for COVID-19
    Ministry of Health List of Approved Offsite Providers for Polymerase Chain Reaction (PCR) Tests for COVID-19 List updated as at 5 March 2021. Service Service Provider Name of Location Address Partnering Lab Provided Offsite PCR Parkway Laboratory Shangri-La Hotel 22 Orange Grove Rd, Singapore 258350 Acumed Medical Group Swab and Services Ltd Serology Parkway Laboratory St Engineering Marine 16 Benoi Road S(629889) Services Ltd Quest Laboratories Pte Offsite PCR Ltd Bukit Batok North N4 432A Bukit Batok West Avenue 8, S(651432) Swab and Q Squared Solutions Serology Ally Health (In Partnership Laboratory With Jaga-Me) National Public Health C882 6A Raeburn Park, S(088703) Laboratory Sands Expo And Convention Centre 10 Bayfront Ave, Singapore 018956 Parkway Laboratory 1 Harbour Front Ave Level 2 Keppel Bay Tower, Services Ltd Keppel Office Singapore 098632 Offsite PCR 40 Scotts Road, #22-01 Environment Building, Swab PUB Office Singapore 228231 The Istana 35 Orchard Rd, Singapore 238823 One Marina Boulevard 1 Marina Boulevard S018989 Rasa Sentosa Singapore 101 Siloso Road S098970 MWOC @ Ponggol Northshore 501A Ponggol Way, Singapore 828646 Bethesda Medical Centre Innovative Diagnostics MWOC @ CCK 10A Lorong Bistari, Singapore 688186 Offsite PCR MWOC @ Eunos 10A Eunos Road 1, Singapore 408523 Swab And Pte Ltd MWOC @ Tengah A 1A Tengah Road, Singapore 698813 Page 1 of 87 MWOC @ Tengah B; 3A Tengah Road, Singapore 698814 Serology Hotel Chancellor 28 Cavenagh / Orchard Road, Singapore 229635 Services Parkway Laboratory Days Hotel (Zhongshan
    [Show full text]
  • Dover Campus at a Glance
    DOVER CAMPUS AT A GLANCE To explore more, please visit www.uwcsea.edu.sg/dover-campus 3,024 167 56 Students at Dover Campus Boarders at Dover Campus Scholars at Dover Campus Capacity per grade at Dover Campus Nationalities at Dover Campus Boarders are enrolled from Grade 8 and above 330 330 296 296 286 Others 26.8% 13.7% India 264 (73 nationalities) 220 198 13% UK 176 154 132 110 Netherlands 2.8% 83 88 88 nationalities France 3.1% 9% USA 36 Korea 4.1% K1 K2 G1 G2 G3 G4 G5 G6 G7 G8 G9 G10 G10 G11 G12 China 5.7% 8.2% Australia UWCSEA curriculum (I)GCSE FIB IBDP Japan 6.2% 7.3% Singapore Infant School Middle School Junior School High School n at oke Do p ve Albanian | Amharic | Arabic | Assamese | Belarusian | Bengali | Bulgarian | Burmese | Catalan | Chinese | Croatian | Czech | Danish | s r s C Dutch | English | Faroese | Finnish | French | Georgian | German | Greek | Gujarati | Hebrew | Hindi | Hungarian | Icelandic | Indonesian e g a m | Irish | Italian | Japanese | Javanese | Kannada | Kazakh | Khmer | Korean | Lao | Lithuanian | Malay | Malayalam | Marathi | Mende a u p | Mongolian | Norwegian | Norwegian Bokmal | Oriya | Pa’o Karen | Panjabi | Persian | Polish | Portuguese | Romanian | Russian | g u n s a Serbian | Sindhi | Sinhala; Sinhalese | Slovak | Slovenian | Spanish; Castilian | Swahili | Swedish | Tagalog | Tamil | Telugu | Thai | Turkish l 70 | Ukrainian | Urdu | Vietnamese | Wolof | Zulu Geographical distribution of enrollment at Dover Campus 27 25 28 24 26 School bus travel time from top residential districts 23 19 20 18 District 10 15–30 minutes 17 22 21 13 11 16 District 5 10–20 minutes 12 14 10 8 15 9 District 9 15–30 minutes 5 7 3 1 6 4 2 <1% 1–10% 10–25% >25% 1.
    [Show full text]
  • Upper Serangoon Open on Thursday 11 Feb 2021
    LIST OF CLINICS IN UPPER SERANGOON OPEN ON THURSDAY 11 FEB 2021 S/N NAME OF CLINIC BLOCK STREET NAME LEVEL UNIT BUILDING POSTAL TELEPHONE OPENING HOURS CODE 1 ACUMED MEDICAL GROUP BLK 215C COMPASSVALE DRIVE 01 02 543215 63850113 8.30AM-12.30PM 2 AFFINITY MEDICAL CLINIC BLK 253 SERANGOON CENTRAL DRIVE 01 187 550253 62808080 8.30AM-1.30PM 3 CALROSE MEDICAL FAMILY CLINIC BLK 231A SUMANG LANE 01 05 MATILDA COURT 821231 69571750 8.30AM-1.00PM 4 COMFORT CLINIC & SURGERY BLK 214 SERANGOON AVE 4 01 100 550214 62807271 8.30AM-12.30PM 5 COMPASSVALE 297A MEDICAL CLINIC BLK 297A COMPASSVALE ST 01 36 541297 65473592 8.30AM-12.30PM 6 DA CLINIC @ ANCHORVALE BLK 351 ANCHORVALE ROAD 01 01 540351 31650144 8.30AM-4.00PM 7 DR JOYCE & PARTNERS FAMILY CLINIC BLK 224A SUMANG LANE 01 01 MATILDA EDGE 821224 69267607 8.30AM-12.00PM 8 EDGEDALE MEDICAL CLINIC BLK 122A EDGEDALE PLAINS 01 187 821122 66352272 9.00AM-1.00PM 9 ETERN MEDICAL CLINIC BLK 70 PUNGGOL CENTRAL 01 05 PUNGGOL MRT STATION 828868 64259935 8.30AM-1.00PM 10 ETERN MEDICAL CLINIC (PUNGGOL SUMANG BLK 308C PUNGGOL WALK 01 302 WATERWAY TERRACES I 823308 62467288 8.30AM-1.00PM LRT) 11 FAITH HEALTHCARE (RIVERVALE) 11 RIVERVALE CRESCENT 02 15 RIVERVALE MALL 545082 63157879 8.30AM-1.00PM 12 FAMILY HEALTHCARE CLINIC & SURGERY BLK 151 SERANGOON NORTH AVE 2 01 35 550151 62889557 8.30AM-12.00PM 13 GARDEN CLINIC BLK 304 SERANGOON AVE 2 01 04 550304 63821878 8.30AM-12.00PM 14 GSH CLINIC & SURGERY PTE.
    [Show full text]
  • Auction & Sales Private Treaty
    Auction & Sales Private Treaty. MARCH 2020: RESIDENTIAL Salespersons to contact: Tricia Tan, CEA R021904I, 6228 7349 / 9387 9668 Gwen Lim, CEA R027862B, 6228 7331 / 9199 2377 Noelle Tan, CEA R047713G, 6228 7380 / 9766 7797 Teddy Ng, CEA R006630G, 6228 7326 / 9030 4603 Lock Sau Lai, CEA R002919C, 6228 6814 / 9181 1819 Sharon Lee (Head of Auction), CEA R027845B, 6228 6891 / 9686 4449 Ong HuiQi (Admin Support) 6228 7302 Website: http://www.knightfrank.com.sg/auction Email: [email protected] LANDED PROPERTIES FOR SALE * Owner's ** Public /Private Trustee's *** Estate's @ Liquidator's @@ Bailiff's % Receiver's # Mortgagee's ## Developer's ### MCST's Approx. Land / Contact S/no District Street Name Tenure Property Type Room Guide Price Remarks Floor Area (sqft) Person MORTGAGEE SALE One of the best location in Sentosa Cove with a picturesque waterway Leasehold 99 2½-Storey Bungalow Noelle / view. Upside potential. Foreigners are eligible to purchase landed # 1 D04 PARADISE ISLAND years wef. with Private Pool and 5- 5 7,045 / 8,170 $9.9M Sau Lai / properties only in Sentosa Cove. 5 ensuite bedrooms. Efficient layout. 07/11/2005 Bedrooms Sharon Private pool & yacht berth. Vacant possession. More Info MORTGAGEE SALE Leasehold 99 2½-Storey Detached Noelle / Scenic waterway view. Unique façade. Internal lift serving all levels. # 2 D04 SANDY ISLAND years wef. House with Basement 7 7,307 / 6,727 $11.3M Sau Lai With private pool and yacht berth. Basement parking with mechanized 13/06/2007 Parking More Info MORTGAGEE SALE Leasehold 2½-Storey Detached Noelle / Lifestyle living with an enchanting waterway view! 4 ensuite bedrooms.
    [Show full text]
  • Illustrated Plans
    K I N L T H R O N N R YISHUN TA E E L S HOUSING & TRANSPORT S E L E TA R N O R T H L I N K Lentor Hills NORTHSHORE DRIVE KHATIB E PUNGGOL POINT I V R D E SAMUDERA C A Punggol Point P PUNGGOL COAST S D O A R P UNGGO O E L CO R A A ERO S A S R T P PA R C A D M R E T TECK LEE A E A V T IE L C E L W E E S T S NIBONG SE S SAM KEE LO E L C K W O N G I G L N T U S P E W R P SELETAR LINK A I T C L E C S E A SUMANG D S I E L L L E Y P T U A N R G G S E A O L E E E L T V R N A I O R R O SUMANG WALK PUNGGOL DRIVE A D S R E R E P SOO TECK PUNGGOL WALKPUNGGOL DAMAI T O S PA C A H C L E I N W K A Y PUNGGOL CENTRAL TA M P I N E S E X P R E S S W AY OASIS PUNGGOL ROAD PUNGGOL WAY PUNGGOL FIELD FERNVALE STREET KADALOOR A COVE NCHORV FARMWAY ALE STR SPRINGLEAF EET KUPANG CHENG LIM TA X P R E S S W AY THANGGAM M TA R E P L E I N MERIDIAN S E D PUNGGOL EAST A E S O S E N G R K JALAN KAYU A N G E A S T W AY R E T IVE X S R VA E L P RIVIERA COMPASSVALE E D R Y W R A I S E L E S S W VE E T E G A R E X P R L S CORAL EDGE E N NT FERNVALE LINK S OR D A A A K FERNVALE ROAD W V O K E R G N G N A I U N N SENGK E A ANG W LAYAR S L Y K E EST AVE E NUE FERNVALE N E U S G CH K L SENGKANG RUMBIA A A IO YIO NG V Y CHU R O KA NG H R OA E C D A ST N A A SENGKANG EAST ROAD TONGKANG V EN U N E UPPER THOMSON ROAD Y O GERALD DRIVE PUNGGOL ROAD BAKAU A R S EN D T W G A K BUANGKOK DRIVE A H S RENJONG O N G SENGKANG EAST DRIVE R S - N S E O D S O R A M U O O LENTOR P R E H A T X S T R K RANGGUNGT R N KANGKAR H A I E E T L P A E K BUANGKOK V P E U L O L E K D L S G C O A N A B O
    [Show full text]