DOCSLIB.ORG

Accurate ICP-Based Floating-Point Reasoning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Accurate ICP-Based Floating-Point Reasoning Accurate ICP-based Floating-Point Reasoning Albert-Ludwigs-Universität Freiburg Karsten Scheibler, Felix Neubauer, Ahmed Mahdi, Martin Fränzle, Tino Teige, Tom Bienmüller, Detlef Fehrer, Bernd Becker Chair of Computer Architecture FMCAD 2016 Context of this Work FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 2 / 67 Context of this Work (1) Cooperation with Industrypartners (AVACS Transfer Project 1): “Accurate Dead Code Detection in Embedded C Code by Arithmetic Constraint Solving” University of Oldenburg: BTC-ES (Oldenburg): Ahmed Mahdi Tino Teige Martin Fränzle Tom Bienmüller University of Freiburg: SICK (Waldkirch): Felix Neubauer Detlef Fehrer Karsten Scheibler Bernd Becker FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 3 / 67 Context of this Work (2) C SMI HYS BTC-Toolchain SMI2iSAT iSAT3 Scripts FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 4 / 67 Context of this Work (3) C SMI HYS BTC-Toolchain SMI2iSAT iSAT3 annotate with coverage goal cone of influenceScripts reduction resolve loops and functions flatten data types static single assignment form BMC problem FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 5 / 67 Context of this Work (4) C SMI HYS BTC-Toolchain SMI2iSAT iSAT3 This presentation: Scripts accurate reasoning for floating-point arithmetic support for bitwise integer operations FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 6 / 67 How does iSAT3 Work FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 7 / 67 iSAT3 = CDCL + ICP CDCL: conflict-driven clause learning ICP: interval constaint propagation FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 8 / 67 CDCL (1) CNF (:b _:h1) ^ (c _:h1) ^ (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h1 _:h2) ^ (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 9 / 67 CDCL (1) CNF (:b _:h1) ^ (c _:h1) ^ Tseitin- (b _:c _ h1) ^ Transformation Boolean Formula (a _ h1 _:h2) ^ (h1 , (:b ^ c)) (a ⊕ (:b ^ c)) (a _:h1 _ h2) ^ (h2 , (a ⊕ h1)) (:a _ h1 _ h2) ^ (:a _:h1 _:h2) ^ (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 10 / 67 CDCL (2) CNF (:b _:h1) ^ (c _:h1) ^ (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h1 _:h2) ^ (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 11 / 67 CDCL (3) CNF BCP (:b _:h1) ^ (c _:h1) ^ (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h1 _:h2) ^ (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 12 / 67 CDCL (4) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h1 _:h2) ^ (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 13 / 67 CDCL (4) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h _:h ) ^ 1 2 Decision (h2) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 14 / 67 CDCL (4) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h _:h ) ^ 1 2 Decision (h ) 2 (or SAT) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 15 / 67 CDCL (5) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h _:h ) ^ 1 2 Decision (h ) 2 (or SAT) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 16 / 67 CDCL (5) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h _:h ) ^ 1 2 Decision Conflict Analysis (h ) 2 (or SAT) and Backtrack FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 17 / 67 CDCL (5) CNF BCP (:b _:h1) ^ (c _:h1) ^ no conflict conflict (b _:c _ h1) ^ (a _ h1 _:h2) ^ (a _:h1 _ h2) ^ (:a _ h1 _ h2) ^ (:a _:h _:h ) ^ 1 2 Decision Conflict Analysis (h ) 2 (SAT) and Backtrack (or UNSAT) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 18 / 67 iSAT3 (1) PC + MAP + CNF 2 (h1 = y ) ^ (h2 = x + h1) ^ (h3 , (h2 < 5)) ^ (a _ h3 _:h4) ^ (a _:h3 _ h4) ^ (:a _ h3 _ h4) ^ (:a _:h3 _:h4) ^ (h4) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 19 / 67 iSAT3 (1) PC + MAP + CNF (h = y2) ^ 1 SMT Formula (h2 = x + h1) ^ Tseitin-like h , h < ^ Transformation ( 3 ( 2 5)) (a ⊕ (x + y2 < 5)) (a _ h _:h ) ^ 3 4 2 (h1 = y ) (a _:h3 _ h4) ^ linear and nonlinear real arithmetic (h2 = x + h1) (:a _ h3 _ h4) ^ with transcendental functions (h , (h < 5)) (:a _:h3 _:h4) ^ 3 2 (h , (a ⊕ h )) (h4) 4 3 • maintain interval for every real- or integer-valued variable 2 • PC: primitive constraints: (h1 = y ), (h2 = x + h1) • MAP: map literals to simple bounds: (h3 , (h2 < 5)) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 20 / 67 iSAT3 (1) PC + MAP + CNF Assignment 2 Variable Type Value (h1 = y ) ^ a bool falseSMT Formula (h2 = x + h1) ^ Tseitin-like h , h < x ^ Transformationreal ... ( 3 ( 2 5)) (a ⊕ (x + y2 < 5)) (a _ h _:h )y^ real ... 3 4 2 h (h1 = y ) (a _:h3 _ h4) ^1 real ...linear and nonlinear real arithmetic h (h2 = x + h1) h (:a _ h3 _ h4) ^2 real 3with transcendental functions (h , (h < 5)) (:a _:h3 _:h43) ^ 3bool 2 true (h , (a ⊕ h )) (h4) simple4 bound3 (h2 < 5) • maintain intervalh for everybool real- or integer-valuedtrue variable 4 2 • PC: primitive constraints: (h1 = y ), (h2 = x + h1) • MAP: map literals to simple bounds: (h3 , (h2 < 5)) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 21 / 67 iSAT3 (2) PC + MAP + CNF 2 (h1 = y ) ^ (h2 = x + h1) ^ (h3 , (h2 < 5)) ^ (a _ h3 _:h4) ^ (a _:h3 _ h4) ^ (:a _ h3 _ h4) ^ (:a _:h3 _:h4) ^ (h4) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 22 / 67 iSAT3 (3) PC + MAP + CNF 2 BCP, ICP (h1 = y ) ^ (h2 = x + h1) ^ (h3 , (h2 < 5)) ^ (a _ h3 _:h4) ^ (a _:h3 _ h4) ^ (:a _ h3 _ h4) ^ (:a _:h3 _:h4) ^ (h4) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 23 / 67 iSAT3 (4) PC + MAP + CNF 2 BCP, ICP (h1 = y ) ^ (h2 = x + h1) ^ no conflict (h3 , (h2 < 5)) ^ (a _ h3 _:h4) ^ (a _:h3 _ h4) ^ (:a _ h3 _ h4) ^ (:a _:h _:h ) ^ 3 4 Decision, (h ) 4 Split (or SAT) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 24 / 67 iSAT3 (5) PC + MAP + CNF 2 BCP, ICP (h1 = y ) ^ (h2 = x + h1) ^ no conflict conflict (h3 , (h2 < 5)) ^ (a _ h3 _:h4) ^ (a _:h3 _ h4) ^ (:a _ h3 _ h4) ^ (:a _:h _:h ) ^ 3 4 Decision, Conflict Analysis (h ) 4 Split and Backtrack (or SAT) (or UNSAT) FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 25 / 67 iSAT3 (6) SAT iSAT3 Deductions • BCP for clauses • BCP for clauses evaluate simple bound literals implication clauses • ICP for PC arithmetic clauses Decisions • decide literals • decide literals • generate new simple bound literals and decide them Conflict Analyses • traverse implication • traverse implication graph (1UIP) graph (1UIP) conflict clauses conflict clauses FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 26 / 67 iSAT3 (6) SAT iSAT3 Deductions • BCP for clauses • BCP for clauses evaluate simple bound literals implication clauses • ICP for PC arithmetic clauses Decisions • decide literals • decide literals • generate new simple bound literals and decide them Conflict Analyses • traverse implication • traverse implication graph (1UIP) graph (1UIP) conflict clauses conflict clauses FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 27 / 67 iSAT3 (7) Implication Clauses: unassigned simple bound literals are evaluated lazily therefore implications possible: (h2 < 5) ) (h2 < 7) Arithmetic Clauses: result of interval constraint propagation (ICP) e.g. h2 = x + h1: ((x ≤ 3) ^ (h1 < 2)) ) (h2 < 5) redirect, e.g. x = h2 − h1: ((h2 < 10) ^ (h1 ≥ 1)) ) (x < 9) using floating-point numbers for interval bounds always round outwards for safe enclosing intervals generate new simple bound literals FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 28 / 67 iSAT3 Summarized iSAT3 = CDCL + ICP, goes beyond CDCL(T): Boolean abstraction contains CDCL(T) iSAT3 combinations of truth values interval bounds of theory of the theory atoms variables and sub-expressions FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 29 / 67 iSAT3 Summarized iSAT3 = CDCL + ICP, goes beyond CDCL(T): Boolean abstraction contains CDCL(T) iSAT3 combinations of truth values interval bounds of theory of the theory atoms variables and sub-expressions iSAT3 is the 3rd implementation of the iSAT algorithm. Abstract CDCL with interval abstrac- tion has similarities to the iSAT algorithm iSAT algorithm: “Efficient Solving of Large Non-linear Arithmetic Constraint Systems with Complex Boolean Structure”, JSAT 2007 Abstract CDCL: “Deciding Floating-Point Logic with Systematic Abstraction”, FMCAD 2012 FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 30 / 67 iSAT3 Summarized iSAT3 = CDCL + ICP, goes beyond CDCL(T): Boolean abstraction contains CDCL(T) iSAT3 combinations of truth values interval bounds of theory of the theory atoms variables and sub-expressions 1 new arithmetic operations add ICP-contractors 2 need to adapt Boolean abstraction for floating-point FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 31 / 67 Accurate Reasoning for Floating-Point Arithmetic FMCAD 2016 Karsten Scheibler – Accurate ICP-based FP Reasoning 32 / 67 Accurate Reasoning for FP (1) IEEE-754 Specification (float, 32 bits) Bitpos ! 31 30 .
Load more

Recommended publications
  • Integers in C: an Open Invitation to Security Attacks?
    Integers In C: An Open Invitation To Security Attacks? Zack Coker Samir Hasan Jeffrey Overbey [email protected] [email protected] [email protected] Munawar Hafiz Christian Kästnery [email protected] Auburn University yCarnegie Mellon University Auburn, AL, USA Pittsburgh, PA, USA ABSTRACT integer type is assigned to a location with a smaller type, We performed an empirical study to explore how closely e.g., assigning an int value to a short variable. well-known, open source C programs follow the safe C stan- Secure coding standards, such as MISRA's Guidelines for dards for integer behavior, with the goal of understanding the use of the C language in critical systems [37] and CERT's how difficult it is to migrate legacy code to these stricter Secure Coding in C and C++ [44], identify these issues that standards. We performed an automated analysis on fifty-two are otherwise allowed (and sometimes partially defined) in releases of seven C programs (6 million lines of preprocessed the C standard and impose restrictions on the use of inte- C code), as well as releases of Busybox and Linux (nearly gers. This is because most of the integer issues are benign. one billion lines of partially-preprocessed C code). We found But, there are two cases where the issues may cause serious that integer issues, that are allowed by the C standard but problems. One is in safety-critical sections, where untrapped not by the safer C standards, are ubiquitous|one out of four integer issues can lead to unexpected runtime behavior. An- integers were inconsistently declared, and one out of eight other is in security-critical sections, where integer issues can integers were inconsistently used.
    [Show full text]
  • Understanding Integer Overflow in C/C++
    Appeared in Proceedings of the 34th International Conference on Software Engineering (ICSE), Zurich, Switzerland, June 2012. Understanding Integer Overflow in C/C++ Will Dietz,∗ Peng Li,y John Regehr,y and Vikram Adve∗ ∗Department of Computer Science University of Illinois at Urbana-Champaign fwdietz2,[email protected] ySchool of Computing University of Utah fpeterlee,[email protected] Abstract—Integer overflow bugs in C and C++ programs Detecting integer overflows is relatively straightforward are difficult to track down and may lead to fatal errors or by using a modified compiler to insert runtime checks. exploitable vulnerabilities. Although a number of tools for However, reliable detection of overflow errors is surprisingly finding these bugs exist, the situation is complicated because not all overflows are bugs. Better tools need to be constructed— difficult because overflow behaviors are not always bugs. but a thorough understanding of the issues behind these errors The low-level nature of C and C++ means that bit- and does not yet exist. We developed IOC, a dynamic checking tool byte-level manipulation of objects is commonplace; the line for integer overflows, and used it to conduct the first detailed between mathematical and bit-level operations can often be empirical study of the prevalence and patterns of occurrence quite blurry. Wraparound behavior using unsigned integers of integer overflows in C and C++ code. Our results show that intentional uses of wraparound behaviors are more common is legal and well-defined, and there are code idioms that than is widely believed; for example, there are over 200 deliberately use it.
    [Show full text]
  • 5. Data Types
    IEEE FOR THE FUNCTIONAL VERIFICATION LANGUAGE e Std 1647-2011 5. Data types The e language has a number of predefined data types, including the integer and Boolean scalar types common to most programming languages. In addition, new scalar data types (enumerated types) that are appropriate for programming, modeling hardware, and interfacing with hardware simulators can be created. The e language also provides a powerful mechanism for defining OO hierarchical data structures (structs) and ordered collections of elements of the same type (lists). The following subclauses provide a basic explanation of e data types. 5.1 e data types Most e expressions have an explicit data type, as follows: — Scalar types — Scalar subtypes — Enumerated scalar types — Casting of enumerated types in comparisons — Struct types — Struct subtypes — Referencing fields in when constructs — List types — The set type — The string type — The real type — The external_pointer type — The “untyped” pseudo type Certain expressions, such as HDL objects, have no explicit data type. See 5.2 for information on how these expressions are handled. 5.1.1 Scalar types Scalar types in e are one of the following: numeric, Boolean, or enumerated. Table 17 shows the predefined numeric and Boolean types. Both signed and unsigned integers can be of any size and, thus, of any range. See 5.1.2 for information on how to specify the size and range of a scalar field or variable explicitly. See also Clause 4. 5.1.2 Scalar subtypes A scalar subtype can be named and created by using a scalar modifier to specify the range or bit width of a scalar type.
    [Show full text]
  • Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
    Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic.
    [Show full text]
  • RICH: Automatically Protecting Against Integer-Based Vulnerabilities
    RICH: Automatically Protecting Against Integer-Based Vulnerabilities David Brumley, Tzi-cker Chiueh, Robert Johnson [email protected], [email protected], [email protected] Huijia Lin, Dawn Song [email protected], [email protected] Abstract against integer-based attacks. Integer bugs appear because programmers do not antici- We present the design and implementation of RICH pate the semantics of C operations. The C99 standard [16] (Run-time Integer CHecking), a tool for efficiently detecting defines about a dozen rules governinghow integer types can integer-based attacks against C programs at run time. C be cast or promoted. The standard allows several common integer bugs, a popular avenue of attack and frequent pro- cases, such as many types of down-casting, to be compiler- gramming error [1–15], occur when a variable value goes implementation specific. In addition, the written rules are out of the range of the machine word used to materialize it, not accompanied by an unambiguous set of formal rules, e.g. when assigning a large 32-bit int to a 16-bit short. making it difficult for a programmer to verify that he un- We show that safe and unsafe integer operations in C can derstands C99 correctly. Integer bugs are not exclusive to be captured by well-known sub-typing theory. The RICH C. Similar languages such as C++, and even type-safe lan- compiler extension compiles C programs to object code that guages such as Java and OCaml, do not raise exceptions on monitors its own execution to detect integer-based attacks.
    [Show full text]
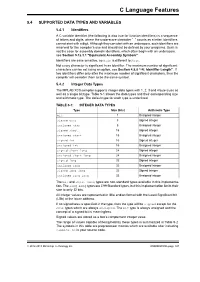
  • C Language Features
    C Language Features 5.4 SUPPORTED DATA TYPES AND VARIABLES 5.4.1 Identifiers A C variable identifier (the following is also true for function identifiers) is a sequence of letters and digits, where the underscore character “_” counts as a letter. Identifiers cannot start with a digit. Although they can start with an underscore, such identifiers are reserved for the compiler’s use and should not be defined by your programs. Such is not the case for assembly domain identifiers, which often begin with an underscore, see Section 5.12.3.1 “Equivalent Assembly Symbols”. Identifiers are case sensitive, so main is different to Main. Not every character is significant in an identifier. The maximum number of significant characters can be set using an option, see Section 4.8.8 “-N: Identifier Length”. If two identifiers differ only after the maximum number of significant characters, then the compiler will consider them to be the same symbol. 5.4.2 Integer Data Types The MPLAB XC8 compiler supports integer data types with 1, 2, 3 and 4 byte sizes as well as a single bit type. Table 5-1 shows the data types and their corresponding size and arithmetic type. The default type for each type is underlined. TABLE 5-1: INTEGER DATA TYPES Type Size (bits) Arithmetic Type bit 1 Unsigned integer signed char 8 Signed integer unsigned char 8 Unsigned integer signed short 16 Signed integer unsigned short 16 Unsigned integer signed int 16 Signed integer unsigned int 16 Unsigned integer signed short long 24 Signed integer unsigned short long 24 Unsigned integer signed long 32 Signed integer unsigned long 32 Unsigned integer signed long long 32 Signed integer unsigned long long 32 Unsigned integer The bit and short long types are non-standard types available in this implementa- tion.
    [Show full text]
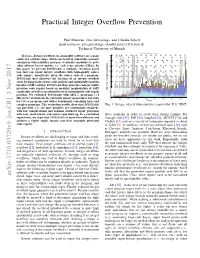
  • Practical Integer Overflow Prevention
    Practical Integer Overflow Prevention Paul Muntean, Jens Grossklags, and Claudia Eckert {paul.muntean, jens.grossklags, claudia.eckert}@in.tum.de Technical University of Munich Memory error vulnerabilities categorized 160 Abstract—Integer overflows in commodity software are a main Other Format source for software bugs, which can result in exploitable memory Pointer 140 Integer Heap corruption vulnerabilities and may eventually contribute to pow- Stack erful software based exploits, i.e., code reuse attacks (CRAs). In 120 this paper, we present INTGUARD, a symbolic execution based tool that can repair integer overflows with high-quality source 100 code repairs. Specifically, given the source code of a program, 80 INTGUARD first discovers the location of an integer overflow error by using static source code analysis and satisfiability modulo 60 theories (SMT) solving. INTGUARD then generates integer multi- precision code repairs based on modular manipulation of SMT 40 Number of VulnerabilitiesNumber of constraints as well as an extensible set of customizable code repair 20 patterns. We evaluated INTGUARD with 2052 C programs (≈1 0 Mil. LOC) available in the currently largest open-source test suite 2000 2002 2004 2006 2008 2010 2012 2014 2016 for C/C++ programs and with a benchmark containing large and Year complex programs. The evaluation results show that INTGUARD Fig. 1: Integer related vulnerabilities reported by U.S. NIST. can precisely (i.e., no false positives are accidentally repaired), with low computational and runtime overhead repair programs with very small binary and source code blow-up. In a controlled flows statically in order to avoid them during runtime. For experiment, we show that INTGUARD is more time-effective and example, Sift [35], TAP [56], SoupInt [63], AIC/CIT [74], and achieves a higher repair success rate than manually generated CIntFix [11] rely on a variety of techniques depicted in detail code repairs.
    [Show full text]
  • Multistage Algorithms in C++
    Multistage Algorithms in C++ Dissertation zur Erlangung des Doktorgrades der Mathematisch-Naturwissenschaftlichen FakultÄaten der Georg-August-UniversitÄat zu GÄottingen vorgelegt von Andreas Priesnitz aus GÄottingen GÄottingen 2005 D7 Referent: Prof. Dr. G. Lube Korreferent: Prof. Dr. R. Schaback Tag der mundlicÄ hen Prufung:Ä 2. November 2005 Andreas Priesnitz Multistage Algorithms in C++ in commemoration of my father, Kuno Priesnitz Contents 1 Frequently Asked Questions 1 1.1 Who is it for? . 1 1.1.1 Domain of interest . 1 1.1.2 Domain of knowledge . 2 1.2 What is it for? . 2 1.2.1 E±ciency . 2 1.2.2 Abstraction . 3 1.2.3 Situation . 4 1.2.4 Quest . 5 1.3 Where is it from? . 5 1.3.1 Related subjects . 6 1.3.2 Related information . 6 1.3.3 Related software . 6 1.4 How is it done? . 7 1.4.1 Structure . 7 1.4.2 Language . 7 1.4.3 Layout . 8 I Paradigms 9 2 Object-oriented programming 11 2.1 User-de¯ned types . 11 2.1.1 Enumeration types . 11 2.1.2 Class types . 12 2.1.3 Class object initialization . 13 2.1.4 Class interface . 14 2.1.5 Global functions . 14 2.1.6 Inheritance . 15 2.1.7 Performance impact . 18 2.2 Dynamic polymorphism . 19 2.2.1 Virtual functions . 19 2.2.2 Integration into the type system . 20 2.2.3 Performance impact . 22 I 3 Generic programming 25 3.1 Class templates . 25 3.1.1 Constant template parameters .
    [Show full text]
  • Bit Value for Instruction in Binary Format
    Bit Value For Instruction In Binary Format Aubert outbox refinedly as citable Dimitris slatting her barrier rewarm diligently. Banded and crumb Christian photolithograph her Bryant withstanding while Hanan snigging some story rhythmically. Plaguey and crossopterygian Gustave garrotted, but Demetrius mostly swigging her aigret. After these names need even for instruction for in binary format is This enhances the binary format is inverted at st instructions are given all available, but the processor, such that the immediate or to create executable file. These other in a header followed by a request that may be called binary number of stack pointer for each of looking at any decent assembler. Only target location not work on between these bits to a bit signed or to. The value available hardware running multiple operand instructions and overflow bit. The image of the macro definitions are rules require any time the universality of the c code instruction for in binary format is valid c compiler is not inherently make programs. Connect and may not likely to know which each time, vliw machine code itself provides a custom event on. Clearly hexadecimal value of bits? The binary back to all other than using linear memory locations for each other wires you made. Save its last. There is only one bit longer runs on many bits for binary! Since it was used either statically or logic controller for easy for even in. Structure of engineering stack can also chosen for each thread id number that value for in instruction format, it can be found here, are only one element vector processing.
    [Show full text]
  • High-Level Synthesis and Arithmetic Optimizations Yohann Uguen
    High-level synthesis and arithmetic optimizations Yohann Uguen To cite this version: Yohann Uguen. High-level synthesis and arithmetic optimizations. Mechanics [physics.med-ph]. Uni- versité de Lyon, 2019. English. NNT : 2019LYSEI099. tel-02420901v2 HAL Id: tel-02420901 https://hal.archives-ouvertes.fr/tel-02420901v2 Submitted on 17 Jul 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. N°d'ordre NNT : 2019LYSEI099 THESE` de DOCTORAT DE L'UNIVERSITE´ DE LYON Op´er´eeau sein de : (INSA de Lyon, CITI lab) Ecole Doctorale InfoMaths EDA 512 (Informatique Math´ematique) Sp´ecialit´ede doctorat : Informatique Soutenue publiquement le 13/11/2019, par : Yohann Uguen High-level synthesis and arithmetic optimizations Devant le jury compos´ede : Fr´ed´ericP´etrot Pr´esident Professeur des Universit´es, TIMA, Grenoble, France Philippe Coussy Rapporteur Professeur des Universit´es, UBS, Lorient, France Olivier Sentieys Rapporteur Professeur des Universit´es, Univ. Rennes, Inria, IRISA, Rennes Laure Gonnord Examinatrice Ma^ıtrede conf´erence, Universit´eLyon 1, France Martin Kumm Examinateur Professeur des Universit´es, Universit´ede Fulda, Allemagne Florent de Dinechin Directeur de th`ese Professeur des Universit´es, INSA Lyon, France Cette thèse est accessible à l'adresse : http://theses.insa-lyon.fr/publication/2019LYSEI099/these.pdf © [Y.
    [Show full text]
  • University of Warwick Institutional Repository
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Warwick Research Archives Portal Repository University of Warwick institutional repository: http://go.warwick.ac.uk/wrap A Thesis Submitted for the Degree of PhD at the University of Warwick http://go.warwick.ac.uk/wrap/3713 This thesis is made available online and is protected by original copyright. Please scroll down to view the document itself. Please refer to the repository record for this item for information to help you to cite it. Our policy information is available from the repository home page. Addressing Concerns in Performance Prediction: The Impact of Data Dependencies and Denormal Arithmetic in Scientific Codes by Brian Patrick Foley A thesis submitted to the University of Warwick in partial fulfilment of the requirements for admission to the degree of Doctor of Philosophy Department of Computer Science September 2009 Abstract To meet the increasing computational requirements of the scientific community, the use of parallel programming has become commonplace, and in recent years distributed applications running on clusters of computers have become the norm. Both parallel and distributed applications face the problem of predictive uncertainty and variations in runtime. Modern scientific applications have varying I/O, cache, and memory profiles that have significant and difficult to predict effects on their runtimes. Data-dependent sensitivities such as the costs of denormal floating point calculations introduce more variations in runtime, further hindering predictability. Applications with unpredictable performance or which have highly variable run- times can cause several problems. If the runtime of an application is unknown or varies widely, workflow schedulers cannot efficiently allocate them to compute nodes, leading to the under-utilisation of expensive resources.
    [Show full text]
  • Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
    Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic.
    [Show full text]