GADT Meet Subtyping
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Integers in C: an Open Invitation to Security Attacks?
Integers In C: An Open Invitation To Security Attacks? Zack Coker Samir Hasan Jeffrey Overbey [email protected] [email protected] [email protected] Munawar Hafiz Christian Kästnery [email protected] Auburn University yCarnegie Mellon University Auburn, AL, USA Pittsburgh, PA, USA ABSTRACT integer type is assigned to a location with a smaller type, We performed an empirical study to explore how closely e.g., assigning an int value to a short variable. well-known, open source C programs follow the safe C stan- Secure coding standards, such as MISRA's Guidelines for dards for integer behavior, with the goal of understanding the use of the C language in critical systems [37] and CERT's how difficult it is to migrate legacy code to these stricter Secure Coding in C and C++ [44], identify these issues that standards. We performed an automated analysis on fifty-two are otherwise allowed (and sometimes partially defined) in releases of seven C programs (6 million lines of preprocessed the C standard and impose restrictions on the use of inte- C code), as well as releases of Busybox and Linux (nearly gers. This is because most of the integer issues are benign. one billion lines of partially-preprocessed C code). We found But, there are two cases where the issues may cause serious that integer issues, that are allowed by the C standard but problems. One is in safety-critical sections, where untrapped not by the safer C standards, are ubiquitous|one out of four integer issues can lead to unexpected runtime behavior. An- integers were inconsistently declared, and one out of eight other is in security-critical sections, where integer issues can integers were inconsistently used. -

Understanding Integer Overflow in C/C++
Appeared in Proceedings of the 34th International Conference on Software Engineering (ICSE), Zurich, Switzerland, June 2012. Understanding Integer Overflow in C/C++ Will Dietz,∗ Peng Li,y John Regehr,y and Vikram Adve∗ ∗Department of Computer Science University of Illinois at Urbana-Champaign fwdietz2,[email protected] ySchool of Computing University of Utah fpeterlee,[email protected] Abstract—Integer overflow bugs in C and C++ programs Detecting integer overflows is relatively straightforward are difficult to track down and may lead to fatal errors or by using a modified compiler to insert runtime checks. exploitable vulnerabilities. Although a number of tools for However, reliable detection of overflow errors is surprisingly finding these bugs exist, the situation is complicated because not all overflows are bugs. Better tools need to be constructed— difficult because overflow behaviors are not always bugs. but a thorough understanding of the issues behind these errors The low-level nature of C and C++ means that bit- and does not yet exist. We developed IOC, a dynamic checking tool byte-level manipulation of objects is commonplace; the line for integer overflows, and used it to conduct the first detailed between mathematical and bit-level operations can often be empirical study of the prevalence and patterns of occurrence quite blurry. Wraparound behavior using unsigned integers of integer overflows in C and C++ code. Our results show that intentional uses of wraparound behaviors are more common is legal and well-defined, and there are code idioms that than is widely believed; for example, there are over 200 deliberately use it. -

5. Data Types
IEEE FOR THE FUNCTIONAL VERIFICATION LANGUAGE e Std 1647-2011 5. Data types The e language has a number of predefined data types, including the integer and Boolean scalar types common to most programming languages. In addition, new scalar data types (enumerated types) that are appropriate for programming, modeling hardware, and interfacing with hardware simulators can be created. The e language also provides a powerful mechanism for defining OO hierarchical data structures (structs) and ordered collections of elements of the same type (lists). The following subclauses provide a basic explanation of e data types. 5.1 e data types Most e expressions have an explicit data type, as follows: — Scalar types — Scalar subtypes — Enumerated scalar types — Casting of enumerated types in comparisons — Struct types — Struct subtypes — Referencing fields in when constructs — List types — The set type — The string type — The real type — The external_pointer type — The “untyped” pseudo type Certain expressions, such as HDL objects, have no explicit data type. See 5.2 for information on how these expressions are handled. 5.1.1 Scalar types Scalar types in e are one of the following: numeric, Boolean, or enumerated. Table 17 shows the predefined numeric and Boolean types. Both signed and unsigned integers can be of any size and, thus, of any range. See 5.1.2 for information on how to specify the size and range of a scalar field or variable explicitly. See also Clause 4. 5.1.2 Scalar subtypes A scalar subtype can be named and created by using a scalar modifier to specify the range or bit width of a scalar type. -

Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic. -

Cross-Platform Language Design
Cross-Platform Language Design THIS IS A TEMPORARY TITLE PAGE It will be replaced for the final print by a version provided by the service academique. Thèse n. 1234 2011 présentée le 11 Juin 2018 à la Faculté Informatique et Communications Laboratoire de Méthodes de Programmation 1 programme doctoral en Informatique et Communications École Polytechnique Fédérale de Lausanne pour l’obtention du grade de Docteur ès Sciences par Sébastien Doeraene acceptée sur proposition du jury: Prof James Larus, président du jury Prof Martin Odersky, directeur de thèse Prof Edouard Bugnion, rapporteur Dr Andreas Rossberg, rapporteur Prof Peter Van Roy, rapporteur Lausanne, EPFL, 2018 It is better to repent a sin than regret the loss of a pleasure. — Oscar Wilde Acknowledgments Although there is only one name written in a large font on the front page, there are many people without which this thesis would never have happened, or would not have been quite the same. Five years is a long time, during which I had the privilege to work, discuss, sing, learn and have fun with many people. I am afraid to make a list, for I am sure I will forget some. Nevertheless, I will try my best. First, I would like to thank my advisor, Martin Odersky, for giving me the opportunity to fulfill a dream, that of being part of the design and development team of my favorite programming language. Many thanks for letting me explore the design of Scala.js in my own way, while at the same time always being there when I needed him. -

RICH: Automatically Protecting Against Integer-Based Vulnerabilities
RICH: Automatically Protecting Against Integer-Based Vulnerabilities David Brumley, Tzi-cker Chiueh, Robert Johnson [email protected], [email protected], [email protected] Huijia Lin, Dawn Song [email protected], [email protected] Abstract against integer-based attacks. Integer bugs appear because programmers do not antici- We present the design and implementation of RICH pate the semantics of C operations. The C99 standard [16] (Run-time Integer CHecking), a tool for efficiently detecting defines about a dozen rules governinghow integer types can integer-based attacks against C programs at run time. C be cast or promoted. The standard allows several common integer bugs, a popular avenue of attack and frequent pro- cases, such as many types of down-casting, to be compiler- gramming error [1–15], occur when a variable value goes implementation specific. In addition, the written rules are out of the range of the machine word used to materialize it, not accompanied by an unambiguous set of formal rules, e.g. when assigning a large 32-bit int to a 16-bit short. making it difficult for a programmer to verify that he un- We show that safe and unsafe integer operations in C can derstands C99 correctly. Integer bugs are not exclusive to be captured by well-known sub-typing theory. The RICH C. Similar languages such as C++, and even type-safe lan- compiler extension compiles C programs to object code that guages such as Java and OCaml, do not raise exceptions on monitors its own execution to detect integer-based attacks. -

Blossom: a Language Built to Grow
Macalester College DigitalCommons@Macalester College Mathematics, Statistics, and Computer Science Honors Projects Mathematics, Statistics, and Computer Science 4-26-2016 Blossom: A Language Built to Grow Jeffrey Lyman Macalester College Follow this and additional works at: https://digitalcommons.macalester.edu/mathcs_honors Part of the Computer Sciences Commons, Mathematics Commons, and the Statistics and Probability Commons Recommended Citation Lyman, Jeffrey, "Blossom: A Language Built to Grow" (2016). Mathematics, Statistics, and Computer Science Honors Projects. 45. https://digitalcommons.macalester.edu/mathcs_honors/45 This Honors Project - Open Access is brought to you for free and open access by the Mathematics, Statistics, and Computer Science at DigitalCommons@Macalester College. It has been accepted for inclusion in Mathematics, Statistics, and Computer Science Honors Projects by an authorized administrator of DigitalCommons@Macalester College. For more information, please contact [email protected]. In Memory of Daniel Schanus Macalester College Department of Mathematics, Statistics, and Computer Science Blossom A Language Built to Grow Jeffrey Lyman April 26, 2016 Advisor Libby Shoop Readers Paul Cantrell, Brett Jackson, Libby Shoop Contents 1 Introduction 4 1.1 Blossom . .4 2 Theoretic Basis 6 2.1 The Potential of Types . .6 2.2 Type basics . .6 2.3 Subtyping . .7 2.4 Duck Typing . .8 2.5 Hindley Milner Typing . .9 2.6 Typeclasses . 10 2.7 Type Level Operators . 11 2.8 Dependent types . 11 2.9 Hoare Types . 12 2.10 Success Types . 13 2.11 Gradual Typing . 14 2.12 Synthesis . 14 3 Language Description 16 3.1 Design goals . 16 3.2 Type System . 17 3.3 Hello World . -

Distributive Disjoint Polymorphism for Compositional Programming
Distributive Disjoint Polymorphism for Compositional Programming Xuan Bi1, Ningning Xie1, Bruno C. d. S. Oliveira1, and Tom Schrijvers2 1 The University of Hong Kong, Hong Kong, China fxbi,nnxie,[email protected] 2 KU Leuven, Leuven, Belgium [email protected] Abstract. Popular programming techniques such as shallow embeddings of Domain Specific Languages (DSLs), finally tagless or object algebras are built on the principle of compositionality. However, existing program- ming languages only support simple compositional designs well, and have limited support for more sophisticated ones. + This paper presents the Fi calculus, which supports highly modular and compositional designs that improve on existing techniques. These im- provements are due to the combination of three features: disjoint inter- section types with a merge operator; parametric (disjoint) polymorphism; and BCD-style distributive subtyping. The main technical challenge is + Fi 's proof of coherence. A naive adaptation of ideas used in System F's + parametricity to canonicity (the logical relation used by Fi to prove co- herence) results in an ill-founded logical relation. To solve the problem our canonicity relation employs a different technique based on immediate substitutions and a restriction to predicative instantiations. Besides co- herence, we show several other important meta-theoretical results, such as type-safety, sound and complete algorithmic subtyping, and decidabil- ity of the type system. Remarkably, unlike F<:'s bounded polymorphism, + disjoint polymorphism in Fi supports decidable type-checking. 1 Introduction Compositionality is a desirable property in programming designs. Broadly de- fined, it is the principle that a system should be built by composing smaller sub- systems. -

Bs-6026-0512E.Pdf
THERMAL PRINTER SPEC BAS - 6026 1. Basic Features 1.) Type : PANEL Mounting or DESK top type 2.) Printing Type : THERMAL PRINT 3.) Printing Speed : 25mm / SEC 4.) Printing Column : 24 COLUMNS 5.) FONT : 24 X 24 DOT MATRIX 6.) Character : English, Numeric & Others 7.) Paper width : 57.5mm ± 0.5mm 8.) Character Size : 5times enlarge possible 9.) INTERFACE : CENTRONICS PARALLEL I/F SERIAL I/F 10.) DIMENSION : 122(W) X 90(D) X 129(H) 11.) Operating Temperature range : 0℃ - 50℃ 12.) Storage Temperature range : -20℃ - 70℃ 13.) Outlet Power : DC 12V ( 1.6 A )/ DC 5V ( 2.5 A) 14.) Application : Indicator, Scale, Factory automation equipments and any other data recording, etc.,, - 1 - 1) SERIAL INTERFACE SPECIFICATION * CONNECTOR : 25 P FEMALE PRINTER : 4 P CONNECTOR 3 ( TXD ) ----------------------- 2 ( RXD ) 2 2 ( RXD ) ----------------------- 1 ( TXD ) 3 7 ( GND ) ----------------------- 4 ( GND ) 5 DIP SWITCH BUAD RATE 1 2 3 ON ON ON 150 OFF ON ON 300 ON OFF ON 600 OFF OFF ON 1200 ON ON OFF 2400 OFF ON OFF 4800 ON OFF OFF 9600 OFF OFF OFF 19200 2) BAUD RATE SELECTION * PROTOCOL : XON / XOFF Type DIP SWITCH (4) ON : Combination type * DATA BIT : 8 BIT STOP BIT : 1 STOP BIT OFF: Complete type PARITY CHECK : NO PARITY * DEFAULT VALUE : BAUD RATE (9600 BPS) - 2 - PRINTING COMMAND * Explanation Command is composed of One Byte Control code and ESC code. This arrangement is started with ESC code which is connected by character & numeric code The control code in Printer does not be still in standardization (ESC Control Code). All printers have a code structure by themselves. -
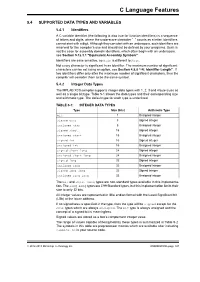
C Language Features
C Language Features 5.4 SUPPORTED DATA TYPES AND VARIABLES 5.4.1 Identifiers A C variable identifier (the following is also true for function identifiers) is a sequence of letters and digits, where the underscore character “_” counts as a letter. Identifiers cannot start with a digit. Although they can start with an underscore, such identifiers are reserved for the compiler’s use and should not be defined by your programs. Such is not the case for assembly domain identifiers, which often begin with an underscore, see Section 5.12.3.1 “Equivalent Assembly Symbols”. Identifiers are case sensitive, so main is different to Main. Not every character is significant in an identifier. The maximum number of significant characters can be set using an option, see Section 4.8.8 “-N: Identifier Length”. If two identifiers differ only after the maximum number of significant characters, then the compiler will consider them to be the same symbol. 5.4.2 Integer Data Types The MPLAB XC8 compiler supports integer data types with 1, 2, 3 and 4 byte sizes as well as a single bit type. Table 5-1 shows the data types and their corresponding size and arithmetic type. The default type for each type is underlined. TABLE 5-1: INTEGER DATA TYPES Type Size (bits) Arithmetic Type bit 1 Unsigned integer signed char 8 Signed integer unsigned char 8 Unsigned integer signed short 16 Signed integer unsigned short 16 Unsigned integer signed int 16 Signed integer unsigned int 16 Unsigned integer signed short long 24 Signed integer unsigned short long 24 Unsigned integer signed long 32 Signed integer unsigned long 32 Unsigned integer signed long long 32 Signed integer unsigned long long 32 Unsigned integer The bit and short long types are non-standard types available in this implementa- tion. -
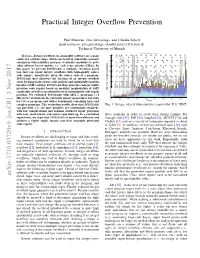
Practical Integer Overflow Prevention
Practical Integer Overflow Prevention Paul Muntean, Jens Grossklags, and Claudia Eckert {paul.muntean, jens.grossklags, claudia.eckert}@in.tum.de Technical University of Munich Memory error vulnerabilities categorized 160 Abstract—Integer overflows in commodity software are a main Other Format source for software bugs, which can result in exploitable memory Pointer 140 Integer Heap corruption vulnerabilities and may eventually contribute to pow- Stack erful software based exploits, i.e., code reuse attacks (CRAs). In 120 this paper, we present INTGUARD, a symbolic execution based tool that can repair integer overflows with high-quality source 100 code repairs. Specifically, given the source code of a program, 80 INTGUARD first discovers the location of an integer overflow error by using static source code analysis and satisfiability modulo 60 theories (SMT) solving. INTGUARD then generates integer multi- precision code repairs based on modular manipulation of SMT 40 Number of VulnerabilitiesNumber of constraints as well as an extensible set of customizable code repair 20 patterns. We evaluated INTGUARD with 2052 C programs (≈1 0 Mil. LOC) available in the currently largest open-source test suite 2000 2002 2004 2006 2008 2010 2012 2014 2016 for C/C++ programs and with a benchmark containing large and Year complex programs. The evaluation results show that INTGUARD Fig. 1: Integer related vulnerabilities reported by U.S. NIST. can precisely (i.e., no false positives are accidentally repaired), with low computational and runtime overhead repair programs with very small binary and source code blow-up. In a controlled flows statically in order to avoid them during runtime. For experiment, we show that INTGUARD is more time-effective and example, Sift [35], TAP [56], SoupInt [63], AIC/CIT [74], and achieves a higher repair success rate than manually generated CIntFix [11] rely on a variety of techniques depicted in detail code repairs. -

Cormac Flanagan Fritz Henglein Nate Nystrom Gavin Bierman Jan Vitek Gilad Bracha Philip Wadler Jeff Foster Tobias Wrigstad Peter Thiemann Sam Tobin-Hochstadt
PC: Amal Ahmed SC: Matthias Felleisen Robby Findler (chair) Cormac Flanagan Fritz Henglein Nate Nystrom Gavin Bierman Jan Vitek Gilad Bracha Philip Wadler Jeff Foster Tobias Wrigstad Peter Thiemann Sam Tobin-Hochstadt Organizers: Tobias Wrigstad and Jan Vitek Schedule Schedule . 3 8:30 am – 10:30 am: Invited Talk: Scripting in a Concurrent World . 5 Language with a Pluggable Type System and Optional Runtime Monitoring of Type Errors . 7 Position Paper: Dynamically Inferred Types for Dynamic Languages . 19 10:30 am – 11:00 am: Coffee break 11:00 am – 12:30 pm: Gradual Information Flow Typing . 21 Type Inference with Run-time Logs . 33 The Ciao Approach to the Dynamic vs. Static Language Dilemma . 47 12:30 am – 2:00 pm: Lunch Invited Talk: Scripting in a Concurrent World John Field IBM Research As scripting languages are used to build increasingly complex systems, they must even- tually confront concurrency. Concurrency typically arises from two distinct needs: han- dling “naturally” concurrent external (human- or software-generated) events, and en- hancing application performance. Concurrent applications are difficult to program in general; these difficulties are multiplied in a distributed setting, where partial failures are common and where resources cannot be centrally managed. The distributed sys- tems community has made enormous progress over the past few decades designing specialized systems that scale to handle millions of users and petabytes of data. How- ever, combining individual systems into composite applications that are scalable—not to mention reliable, secure, and easy to develop maintain—remains an enormous chal- lenge. This is where programming languages should be able to help: good languages are designed to facilitate composing large applications from smaller components and for reasoning about the behavior of applications modularly.