DOCSLIB.ORG

Andreev Reflection Adjusting in the Multi-Terminal Device with the Kink States

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Andreev Reflection Adjusting in the Multi-Terminal Device with the Kink States Andreev reflection adjusting in the multi-terminal device with the kink states Lin Zhang1;3, Chao Wang∗1;2, Peipei Zhang1, and Yu-Xian Li∗1 1College of Physics and Hebei Advanced Thin Film Laboratory, Hebei Normal University, Shijiazhuang 050024, People's Republic of China 2College of Physics, Shijiazhuang University, Shijiazhuang 050035, People's Republic of China 3Shool of Mathematics and Science, Hebei GEO University, Shijiazhuang 050031, People's Republic of China (Dated: June 14, 2021) At the domain wall between two regions with the opposite Chern number, there should be the one-dimensional chiral states, which are called as the kink states. The kink states are robust for the lattice deformations. We design a multi-terminal device with the kink states to study the local Andreev reflection and the crossed Andreev reflection. In the three-terminal device the local Andreev reflection can be suppressed completely for either "0 = 0:5∆s and V0 = 0:1t or "0 = −0:5∆s and V0 = −0:1t, where "0 is the on-site energy of the graphene terminals and V0 is the stagger energy of the center region. The coefficient of the crossed Andreev reflection can reach 1 in the four-terminal device. Besides adjusting the phase difference between superconductors, the local Andreev reflection and the crossed Andreev reflection can be controlled by changing the on-site energy and the stagger energy in the four-terminal device. Our results give some new ideas to design the quantum device in the future. I. INTRODUCTION terminal 2 A S B Topological insulator[1] has been one of the no- + terminal 3 ticeable advanced materials due to the novel physical − properties[2,3], such as quantum Hall effect[4,5] and W quantum spin Hall effect[6,7]. It is of great significance to terminal 1 study the properties of topological insulator for develop- + ing a new generation of quantum components. Recently, y − the quantum anomalous Hall effect has been identified in o x S the three-dimensional magnetic topological insulator[8{ terminal 4 11], which opens new possibilities for chiral-edge-state- L based devices in zero external magnetic field[12, 13]. The chiral states can also appear at the domain walls be- FIG. 1. (Color online) The schematic diagram of the four- tween two regions with the opposite Chern number[14]. terminal device with the kink states. The terminal 1 and 3 are For example, the graphene can be gapped by the sublat- the graphene ribbons. The width and the length of the central tice symmetry breaking staggered on-site energy, which region are W = 8 and L = 28, respectively. The terminal 2 and 4 are the superconductors. In the center region marked is showed in Fig.1. There are one-dimensional states[15{ 0+0(green), the on-site energy is " = V and " = −V , 18], which are referred to as kink states below, pre- A 0 B 0 where V0 is called as the stagger energy. In the region marked 0 0 senting at the boundaries between regions with different − (orange), "A = −V0 and "B = V0. The kink states are at quantized Hall conductances in the graphene nanorib- the interface between two regions with the opposite stagger bon. A Majorana fermion, which is its own antipar- energy. ticle, has the potential for quantum computing. Over . the last two decades it has been realized that Majorana fermions can emerge at zero-energy modes in topologi- cal superconductors[19{21]. After the chiral Majorana dreev reflection come from the different valleys in the edge modes in the quantum anomalous Hall insulator- graphene-superconductor device[30{32]. superconductor structure is realized in the experiment, In this paper, we calculate the transmission coefficients there are more researches focused on the topological su- in a two-terminal device, where there are lattice deforma- perconductor device[23{29]. tions around the domain wall. The transmission coeffi- At the interface between a superconductor and a nor- cients are close to 1 in the two-terminal device, which mal conductor, an incident electron from the normal con- proves the robustness of the kink states[15{17]. Then ductor can be reflected as a hole, which is called Andreev we study the Andreev reflection in the four-terminal de- arXiv:2106.06146v1 [cond-mat.mes-hall] 11 Jun 2021 reflection. When the bias voltage is lower than the su- vice with the topological kink states showed in Fig.1. perconductor gap, the conductance of the superconduc- Through calculating the coefficients of the Andreev re- tor hybrid device is mainly determined by the progress flection in the four-terminal device, we find that the of the Andreev reflection. Keeping to the time-reversal progress of the crossed Andreev reflection can be con- symmetry, the electron and the hole taking part in An- trolled by adjusting the on-site energy and the stagger 2 energy. We now turn to analyze the process that an inci- The rest of this paper is arranged as follows. In Sec.II, dent electron from the graphene terminal is reflected the model Hamiltonian for the system is presented into a hole with a Cooper pair emerging in the su- and the formulas for calculating the Andreev reflection perconductor terminal. Using nonequilibrium Green's coefficients are derived. Our main results are shown function method, we can calculate the retarded and ad- r a y and discussed in Sec.III. Finally, a brief conclusion is vanced Green's function G (E) = [G ] = 1=(EI HC P r − − presented in Sec.IV. α Σα), where HC is the Hamiltonian of the center re- gion in the Nambu representation and I is the unit ma- r r trix with the same dimension as HC . Σα = tcgα(E)tc is the retarded self-energy due to the coupling to the r II. MODEL AND METHOD terminal α, where gα(E) is the surface Green's func- tion of the terminal α. We can numerically calcu- The four-terminal device with the kink states is showed late the surface Green's function of the graphene termi- in Fig.1, where the terminal 1 and 3 are the normal nals. For superconductor terminals, the surface Green's graphene ribbons and the terminal 2 and 4 are super- function[23, 25, 27] in real space is conductors. The center region is the colour region. The 1 ∆=E kink states are at the interface between the regions with gr (E) = iπρβ(E)J [k (x x )] ; (5) α,ij 0 f i j ∆∗=E 1 different colour. Along the x direction and the y direc- − tion they are zigzag and armchair, respectively. The total where α = 2; 4 and ρ is the density of normal Hamiltonian of this junction can be represented as electron states. J0[kf (xi xj)] is the Bessel func- − tion of the first kind with the Fermi wavevector kf . H = HC + HG + HS + HT ; (1) p 2 2 β(E) = iE= ∆s E for E < ∆s and β(E) = p 2 − 2 − j j whereH , H , H and H are the Hamiltonian of the E = E ∆ for E > ∆s. C G S T j j − s j j center region, the graphene nanoribbons, the supercon- The Andreev reflection coefficients for the incident ductor terminals and the coupling between the center electron coming from the graphene terminal 1 can be region and the superconductor terminals, respectively. obtained[23] by In the tight-binding representation, HC and HG are r a TA;11(E) = Tr Γ1;""G Γ1;##G ; given by f "# #"g r a TA;13(E) = Tr Γ1;""G Γ3;##G ; (6) X y X y f "# #"g HC=G = "0anan [tanam + H:c:]; (2) n − <m;n> where the subscripts , , and represent the 11, 22, 12 and 21 matrix"" ## elements,"# respectively,#" in the y where an and an are the creation operator and annihila- Nambu representation. The linewidth function Γα is r r y tion operators of the nth point. " is the on-site energy in defined with the aid of self-energy as Γα = i[Σ (Σ ) ]. 0 α − α the graphene terminals and the center region. In the cen- TA;11 and TA;13 represent the coefficients of the local ter region, "0 = V0 for the different partition, where V0 Andreev reflection and the crossed Andreev reflection, is the stagger energy± of A and B sublattice. The second respectively. Because the Andreev reflection from an term in Eq. (2) stands for the nearest-neighbor hopping electron to a hole is equivalent to that from a hole to an Hamiltonian. Considering that the center region is di- electron under particle-hole symmetry, in this work we rectly coupled to the superconductor terminals, we use only consider the Andreev reflection, where an incident the BCS Hamiltonian for the superconductor terminals electron is reflected as a hole. described by a continuum model, X y X ∗ y y HS = " C C + (∆C C + ∆ C C ); (3) k k σ k σ k # −k " −k " k # k ,σ k III. NUMERICAL RESULTS AND ANALYSIS iθ where ∆ = ∆se . Here ∆s is the superconductor gap In numerical calculations, we set the nearest-neighbour and θ is the superconductor phase. The coupling between hopping energy t = 2:75eV . The length of the nearest- superconductor terminals and graphene is described by neighbor C-C bond is set to be a0 = 0:142 nm as in a X y real graphene sample. The superconductor gap is set to HT = tcan,σCσ(xi) + H:c: (4) −1 − be ∆s = 0:02t and the Fermi wavevector kf = 10 nm . n,σ For the convenience of discussing the influence of the kink Here xi and n represent the positions of the coupling states on Andreev reflection, The Fermi energy Ef is set atoms on the interface of superconductor and the center to be zeros in our calculations for the convenient.
Load more

Recommended publications
  • Download Article (PDF)
    International Conference on Social Science, Education Management and Sports Education (SSEMSE 2015) Study on Present Situation of Full-time Engineering Master in Hebei Province Qingqing Huo, &Jinqiang Geng Shijiazhuang University of Economics, Shijiazhuang, 050031, China Dongye Liu Hebei University of Economics and Business, Shijiazhuang, 050061, China ABSTRACT: Through investigation, this paper analyzes the present situation of full-time engineering master in Hebei province, through the methods of document data, information collecting, questionnaire survey and qualitative analysis. This investigation contains three parts, which are enrollment, education goal and process of training. At last, suggestions are introduced to lay theoretical foundation for the training of full-time engineering master in Hebei Province. And in practice, this research is helpful for the training system to build its standards which accommodate the goal of training application oriented talents. KEYWORD: Present Situation; Full-time Engineering Master; Hebei Province 1 INTRODUCTION 2.2 Object of Study This research investigates the class of 2010、2011 Since the enrollment of full-time engineering master, and 2012 graduate students, who are from 8 universities pay more attention to this job. To ensure universities of 20 fields. the training quality and provide high level talents for the society, universities make relevant rules and regulations based on the documents of education 2.3 Research Contents ministry. But for most of the universities, the The questionnaire contains three parts: enrollment, training of full-time engineering master is a new education goal and process of training. theme. It is different from the training of master of (1) Enrollment is about enrollment motivation and engineering science and non full-time engineering attitude, the awareness of engineering master.
    [Show full text]
  • Intouch T E R T I a R Y C O L L E G E S G R O U P NZTC’S International Newsletter Specialising in Early Childhood Teacher Education
    New Zealand Tertiary College intouch T E R T I A R Y C O L L E G E S G R O U P NZTC’s International Newsletter Specialising in early childhood teacher education May 2014 GRADUATES CONSIDERING AUSTRALIA WE HAVE GREAT NEWS Our Bachelor of Teaching (Early Childhood Education) has been approved by the Australian Children’s Education and Care Quality Authority (ACECQA), the body governing early childhood education in Australia. The approval allows graduates to be granted early childhood teacher (ECT)* status in all Australian states and territories without having to apply for an assessment of their qualification. Harpreet Singh, who now resides in Melbourne, has recently been granted ECT status: “Having ECT status has lots of benefits, like increasing my employability and chances of getting a better salary,” says Harpreet, “and it’s further international recognition of my degree that I worked hard to gain.” Graduates who want to be granted ECT status can apply through the ACECQA website. NZTC’s Bachelor of Teaching (Early Childhood Education) is listed under code PC9727. A certificate confirming ECT status will be sent in the post. * The early childhood sector in Australia differs from the one in New Zealand. There are three different levels of teachers - ‘educators’ who hold a Level 3 qualification, ‘educators’ who can supervise other educators and hold a Level 5 or 6 qualification; and ‘early childhood teachers’ who hold a degree and have a management position around curriculum and teaching. Harpreet Singh 18 CITIES,100 EDUCATIONAL PARTNERS, 39 DAYS NZTC Marketing representatives working in Asia and beyond NZTC marketing representatives travelled to 18 cities in China, South East Asia, Sri Lanka and India last March and April.
    [Show full text]
  • A Complete Collection of Chinese Institutes and Universities For
    Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21.
    [Show full text]
  • University of Leeds Chinese Accepted Institution List 2021
    University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams.
    [Show full text]
  • Zhimin Wang, Ph.D., CFA Curriculum Vitae
    Zhimin Wang, Ph.D., CFA Curriculum Vitae Education: Ph.D. Southern Illinois University Carbondale, U.S.A., 2008, GPA 3.95/4.00 M.A. Shanghai University of Finance and Economics, Shanghai, China, 2003 B. A. Hebei University of Economics and Business, China, 1997 Fields of Specialization (Doctoral Studies): Finance, International Economics Teaching Experience: Associate Professor of Finance, New Jersey City University, Fall 2015‒present Associate Professor of Business Administration, East Central University, Fall 2014‒Spring 2015 Assistant Professor of Business Administration, East Central University, Fall 2008‒Spring 2014 Instructor, Introduction to Microeconomics, Southern Illinois University Carbondale, Fall 2007 and Spring 2008 Instructor, Financial Management, Night School of Shanghai University of Finance and Economics, China, Fall 2001 and Spring 2002 Other Work Experience: Financial Supervisor, Shanghai Securities Co., Ltd., Shanghai, China, June 2003‒August 2004 Project Manager (part time), Huajie Credit Risk Rating Co., Ltd., Shanghai, China, May 2002‒ September 2002 Manager Assistant, Hebei Company of Industrial Trade, Hebei, China, August 1997‒August 2000 Finance Courses Taught at NJCU: Corporate Financial Management, Managerial Economics, Risk Management and Insurance Planning, Portfolio Analysis, Capital Markets and Financial Institutions, International Finance, Managerial Finance, Financial Institutions and Banking Relations Professional Certificates: Chartered Financial Analyst (CFA), 2014 Passed CPA Business Environment and Concepts (BEC) exam, 2010 SAC Securities Qualification, 2004 Qualification Certificate of Specialty and Technology in Accounting, 2004 1 Refereed Journal Publications: Wang, Z., Ettinger, M., Xie, Y., Li, X., 2020. The cost of capital: U.S.-based multinational corporations versus U.S. domestic corporations. Global Finance Journal 44, 13 pages. Wang, D., Wang, Z., Xie.
    [Show full text]
  • 1 Please Read These Instructions Carefully
    PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies.
    [Show full text]
  • Of the Students, by the Students, and for the Students
    Of the Students, By the Students, and For the Students Of the Students, By the Students, and For the Students: Time for Another Revolution Edited by Martin Wolff Of the Students, By the Students, and For the Students: Time for Another Revolution, Edited by Martin Wolff This book first published 2010 Cambridge Scholars Publishing 12 Back Chapman Street, Newcastle upon Tyne, NE6 2XX, UK British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Copyright © 2010 by Martin Wolff and contributors All rights for this book reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the copyright owner. ISBN (10): 1-4438-2565-4, ISBN (13): 978-1-4438-2565-8 English has become the gatekeeper to higher education and employment in China. This book is dedicated to all of those who are unable to unlock the gate and pass through. CET 4 and CET 6 National English examinations have become the symbol of English proficiency in reading and writing. Employers have required them as prerequisite to employment consideration. All comments of students quoted in this book were written by post-graduate students who have passed CET 4 and some have passed CET 6; and the comments were created on computers equipped with Microsoft WORD. The students’ comments are unedited to reflect their true lack of English competency and to debunk the claim that CET 4 and CET 6 reflect any appreciable English writing proficiency, particularly with the availability of the “spell function” of WORD.
    [Show full text]
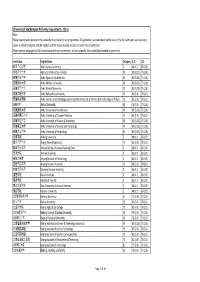
  • University of Southampton PGT Entry Requirements ‐ China Note: These Requirements Represent the Standard Entry Criteria for Our Programmes
    University of Southampton PGT entry requirements ‐ China Note: These requirements represent the standard entry criteria for our programmes. All applications are considered on the basis of the full submission, and so strong scores in relevant subjects and the suitability of the course studied will also be taken into consideration. Please see our webpages for full information and entry requirements, including specific School and Departmental requirements. Institution English Name Category 2:1 2:2 阿坝师范学院 Aba Teachers University Z 88 (3.7) 83 (3.5) 河北农业大学 Agricultural University of Hebei X3 80 (3.25) 75 (2.8) 安徽农业大学 Anhui Agricultural University X3 80 (3.25) 75 (2.8) 安徽医科大学 Anhui Medical University X3 80 (3.25) 75 (2.8) 安徽师范大学 Anhui Normal University X3 80 (3.25) 75 (2.8) 安徽工程大学 Anhui Polytechnic University Y2 83 (3.5) 78 (3.1) 安徽科技学院 Anhui Science and Technology University (AKA University of Science And Technology of Anhui) Y2 83 (3.5) 78 (3.1) 安徽大学 Anhui University X2 78 (3.1) 73 (2.6) 安徽建筑大学 Anhui University of Architecture X3 80 (3.25) 75 (2.8) 安徽中医药大学 Anhui University of Chinese Medicine Y2 83 (3.5) 78 (3.1) 安徽财经大学 Anhui University of Finance & Economics X3 80 (3.25) 75 (2.8) 安徽理工大学 Anhui University of Science and Technology X3 80 (3.25) 75 (2.8) 安徽工业大学 Anhui University of Technology X3 80 (3.25) 75 (2.8) 安康学院 Ankang University Z 88 (3.7) 83 (3.5) 安庆师范大学 Anqing Normal University Y2 83 (3.5) 78 (3.1) 鞍山师范学院 Anshan Normal University Liaoning China Z 88 (3.7) 83 (3.5) 安顺学院 Anshun University Z 88 (3.7) 83 (3.5) 安阳工学院 Anyang Institute of Technology
    [Show full text]
  • Hebei WLAN Area 1/16
    Hebei WLAN area NO. SSID Location_Name Location_Type Location_Address City Province The Second Floor, Fifth Floor of Student Apartment Block A, Cangzhou Vocational 1 ChinaNet School Cangzhou Hebei Vocational College Student Apartment Block A College The Second Floor, Fifth Floor of Student Apartment Block D, Cangzhou Vocational 2 ChinaNet School Cangzhou Hebei Vocational College Student Apartment Block D College The Second Floor, Fifth Floor of Student Apartment Block E, Cangzhou Vocational 3 ChinaNet School Cangzhou Hebei Vocational College Student Apartment Block E College 4 ChinaNet School The Second Floor of Main Office Building, Cangzhou Vocational College Cangzhou Hebei Main Office Building of Vocational College 5 ChinaNet School No.38, Huayan North Road, Tangshan, Hebei Tangshan Hebei Tangshan College Student Dormitory No.4 Building 6 ChinaNet School No.38, Huayan North Road, Tangshan, Hebei Tangshan Hebei Tangshan College Student Dormitory No.5 Building 7 ChinaNet School No.38, Huayan North Road, Tangshan, Hebei Tangshan Hebei Tangshan College Student Dormitory No.6 Building 8 ChinaNet North China Coal Medical University Dormitory 101 School No.57, Jianshe South Road, Tangshan, Hebei Tangshan Hebei 9 ChinaNet North China Coal Medical University Dormitory 102 School No.57, Jianshe South Road, Tangshan, Hebei Tangshan Hebei 10 ChinaNet North China Coal Medical University Dormitory 103 School No.57, Jianshe South Road, Tangshan, Hebei Tangshan Hebei 11 ChinaNet North China Coal Medical University Dormitory 104 School No.57, Jianshe
    [Show full text]
  • Title of Paper
    International Conference on Social Science, Education Management and Sports Education (SSEMSE 2015) Analysis of Mode of Cultural-industry Talents Training at Independent Colleges in Hebei Province Hong ZHANG & Jia LIU & Libo SHI & Cheng CHENG Polytechnic College, Hebei University of Science and Technology, Shijiazhuang, Hebei, China ABSTRACT: With the advent of the era of global information, the culture is playing an increasingly important role in society. The cultural industry is becoming the “sunrise industry” along with the revolution of new science and technology and thus gets more and more attention. However, the development of the cultural industry faces the bottleneck of lacking the professionals of cultural industry. Therefore, for the independent colleges where a large number of talents are cultivated and exported to the society, they should take the obligatory responsibility for cultivating and exporting applicationoriented and innovative talents of cultural industry in order to provide a strong talent and intelligence support and new impetus for the prosperity of the cultural development as well as in Hebei Province. This article analyzes the current situation of cultural industry talents training in Hebei province, focuses on an integrated cultural industry talents training model at independent colleges in Hebei, which is feasible to independent colleges and has great impact upon the strategic cultural development in Hebei. KEYWORD: Hebei province; cultural- industry talents; personnel training mode 1 INTRODUCTION In recent years, China's cultural industry has been 2 ANALYSIS OF THE CURRENT SITUATION developing increasingly in large scale, contributing IN HEBEI CULTURE INDUSTRY TALENTS more and more to the national gross product and the IN COLLEGES AND UNIVERSITIES economy.
    [Show full text]
  • Effect of Computer Multimedia Assisted Word Annotation on Incidental Vocabulary Acquisition of English Reading
    Paper—Effect of Computer Multimedia Assisted Word Annotation on Incidental Vocabulary… Effect of Computer Multimedia Assisted Word Annotation on Incidental Vocabulary Acquisition of English Reading https://doi.org/10.3991/ijet.v14i13.10705 Mengqing Han Shijiazhuang University of Applied Technology, Shijiazhuang, China Shanshan Niu (*) Huaxin College of Hebei GEO University, Shijiazhuang, China [email protected] Abstract—This paper aims at researching the effect of computer multimedia assisted word annotation on incidental vocabulary acquisition of English reading of Chinese students. An empirical research experiment is designed based on the ideas of word annotation, incidental vocabulary acquisition, multimedia annotation, and so on. Through analyzing, three main problems are put forward in this paper. In the empirical experiment, two variables of different annotation modes and subjects’ English levels are designed and immediate test and delayed test are adopted. By selecting suitable test subjects, test materials and test tool, an empirical research has been conducted and the corresponding conclusions have been drawn. The re-search takes the effect of individual English level differences on incidental vocabulary acquisition of English reading and the experimental result play a positive role in the selection of suitable computer assisted annotation modes for students of different English levels. Keywords—Computer multimedia, word annotation, incidental vocabulary acquisition, empirical research 1 Introduction English vocabulary is the cornerstone of English learning and the level of English vocabulary is related to the levels of all aspects, such as English listening, speaking, reading and writing. Researches show that the learning of English vocabulary is not only obtained through English vocabulary teaching, but can be acquired in incidental acquisition by various learning modes, such as English reading, English listening comprehension, and English writing.
    [Show full text]
  • List of Regular Institutions of Higher Education In
    Table 1 List of Regular Institutions of Higher Education in China (As of May 23th, 2011) (Total number：820) Serial Level of Name of Institution Affiliation Location Remarks No.
    [Show full text]