Scrabble on the Tetrascale
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Scrabble Word List 2016
Scrabble Word List 2016 2 – LETTER WORDS AA: n pl. –S rough, cindery lava EX: n pl. EXES the letter X AB: n pl. –S an abdominal muscle FA: n pl. –S the fourth tone of the diatonic AD: n pl. –S an advertisement musical scale AE: adj one FE: n –FES a Hebrew letter AG: adj pertaining to agriculture FY: an expression of disgust – Can be AH: interj – used to express delight, relief, extended with “S” or contempt GI: a judo or karate costume AI: n pl. –S a three-toed sloth GO: v WENT, GONE, GOING, GOES to move AL: n pl. –S an East Indian tree along AM: present 1st person sing. of BE GU: a simple violin used in Shetland (also AN: indefinite article – used before words GJU, GUE) beginning with a vowel HA: n pl. –S a sound of surprise AR: n pl. –S the letter R HE: n pl. –S a male person AS: adv to the same degree HI: interj – used as a greeting AT: prep in the position of HM: interj – used to express thoughtful AW: interj – used to express protest, disgust, consideration or disbelief HO: interj – used to express surprise AX: v –ED, -ING, -ES to work on with an ax (a ID: n pl. –S a part of the psyche type of cutting tool) IF: n pl. –S a possibility AY: n pl. –S aye IN: v INNED, INNING, INS to harvest BA: n pl. –S the eternal soul in Egyptian IO: a cry of joy mythology IS: v present 3rd person sing. -
Ages 8+ 1+ Players
AGES 8+ ® 1+ PLAYERS BRAND ® Contents: SCRABBLE BOGGLE Game with Electronic Timer Object Find as many words as you can in the 4 x 4 letter grid. To win, be the player with the highest score at the end of a 3-minute game; or be the first player to reach the designated point limit in a tournament game. Or practice by yourself to beat your personal best! How to Play Players sit around the table so that everyone can see the Boggle grid when it’s in play. Each player will need a pencil and paper (not included). To start the game, do the following: 1. Turn the lid clockwise as far as it will go, to lower the grid base. See Figure 1. Figure 1. 2. Shake the letter cubes to mix them up. If necessary, jiggle the cubes until they fall into place in the grid base. 1211A0420000 Aa SCRABBLE BOGGLE Instructions (US) 3. Now turn the lid counterclockwise as far as it will go, making sure the letter cubes are lying flat in the base. See Figure 2. The timer light in the Boggle “o” will flash on to begin the countdown! Figure 2. ® BRAND ® The timer light will flash green at first, then orange, and finally red when time is running out. 4. Now quickly place the game in the center of the play area, and all players start looking for words. Finding Words Search the assortment of letters for words of three or more letters. Words are formed from letters that adjoin in sequence horizontally, vertically or diagonally in any direction. -

Acquire: Fun-And-Fortune Game for 2 Players. 1 Hour 15 Min Game Time
List of 2-player games available to borrow from Bowdoin Board Game Club: Acquire: fun-and-fortune game for 2 players. 1 hour 15 min game time. Beyond Baker Street: A card-based Sherlock Holmes mystery game. 30 min game time. Carcassonne the Castle: the two-player version of the classic. 30-45 min game time. Chess: two players battle to death. Game time varies. Clans: A board game set in late pre-history. Easy rules, challenging game. 30 min game time. Cosmic Encounter: the sci fi game for everyone. Very cool board. “A teeth-gritting, mind-croggling, marvelously demanding exercise in ‘what if’.” – Harlan Ellison Coup: Only one can survive. Secret identities, deduction, deception. 15 game time. El Grande Big Box – (includes 6 expansions): Spain in the late middle ages, win with cunning and guile. 60 min game time. Evolution: A dynamic game of survival. 60 min game time. FLUXX: The card game with ever-changing rules. 5-30 min game time. Forbidden Island: Adventure if you DARE! 30 min game time. Gobblet: The fun strategy board game for 2. 10-20 min game time. Grifters: are you devious enough to rob the corporations blink, swindle your opponent and pull off daring heists? 30 game time. Hanabi: A cooperative firework launching game for 2. 30 min game time. Inis: immerse yourself in celtic legends. A truly beautiful game. 60 min game time. Jaipur: A subtle trading game for 2 players. 30 min game time. King of New York: You are a giant monster and you want to become King of New York. -

Simpsons Comics- Colossal Compendium: Volume 4 PDF Book
SIMPSONS COMICS- COLOSSAL COMPENDIUM: VOLUME 4 PDF, EPUB, EBOOK Matt Groening | none | 27 Sep 2016 | Titan Books Ltd | 9781783296552 | English | London, United Kingdom Simpsons Comics- Colossal Compendium: Volume 4 PDF Book Burns Mr. Burns commandeers the Springfield public beach in the middle of a heat wave; Ralph gets left home alone, Duffman shows his esprit de corps by carrying his message to the ends of the universe; Milhouse takes on an impossible mission; Cletus lays down the law in the backwoods; and McBain faces his archenemy The Left Behinders! Qty: 1 2 3. Modified on October 4, , at Use your keyboard! July 15, Burns forces Lisa to battle him in a game of Scrabble; she accepts and after a while she gets upset and smashes the board. So one issue might be issue , the next and the next etc. This will not affect the original upload Small Medium How do you want the image positioned around text? Many Simpsons Comics have been reprinted and collected in trade paperbacks by the American publisher HarperCollins since It has been published around September— October, for Halloween , every year since Ow, Quit It! Stock photo. Seasons 1—20 Seasons 21—present. The postman turns out to be Ned Flanders and while he gives her a tour through the wondrous world they get caught by Mr. Comment and Save Until you earn points all your submissions need to be vetted by other Comic Vine users. Folio: The Magazine for Magazine Management via findarticles. The third and the rarest variant was a reprint of the comic and it had the top right portion of Bart Simpson's head covered over the original bar code. -

30 Minutes Aggravation 2-6 Players Ages 6+ Playing Time
7 Wonders 2-7 players Ages 10+ Playing Time: 30 minutes Aggravation 2-6 players Ages 6+ Playing Time: 45 minutes Agricola 1-5 players Ages 12+ Playing Time: 30 minutes–1.5hours Apples to Apples 4-10 players Ages 10+ Playing Time: 30 minutes Apples to Apples Junior 4-8 players Ages 9+ Playing Time: 30 minutes Arkham Horror 1-8 players Ages 12+ Playing Time: 2-4 hours Axis & Allies Europe 2-4 players Ages 12+ Playing Time: 3.5 hours Axis & Allies 2-5 players Ages 12+ Playing Time: 3 hours Backgammon 2 players Ages 8+ Playing Time: 30 minutes BANG! 4-7 players Ages 8+ Playing Time: 20-40 minutes Battle Cry 2 players Ages 10+ Playing Time: 45 minutes Battleship 2 players Ages 8+ Playing Time: 30 minutes Battlestar Galactica 3-6 players Ages 8+ Playing Time: 2-3 hours Betrayal at House on the Hill 3-6 players Ages 12+ Playing Time: 1 hour Blokus 2-4 players Ages 5+ Playing Time: 20 minutes Bohnanza 2-7 players Ages 13+ Playing Time: 45 minutes Boss Monster 2-4 players Ages 13+ Playing Time: 20 minutes Candy Land 2-4 players Ages 3+ Playing Time: 30 minutes Carcassonne 2-5 players Ages 8+ Playing Time: 30-40 minutes Caverna: The Cave Farmers 1-7 players Ages 12+ Playing Time: 30 minutes-3.5 hours Checkers 2 players Ages 6+ Playing Time: 30 minutes Chess 2 players Ages 6+ Playing Time: 1 hour Chutes & Ladders 2-6 players Ages 3+ Playing Time: 30 minutes Clue 3-6 players Ages 8+ Playing Time: 45 minutes Clumsy Thief 2-6 players Ages 8+ Playing Time: 15 minutes Concept 4-12 players Ages 10+ Playing Time: 40 minutes Connect 4 2 players Ages 6+ -

May 2021 Martin Center Program Calendar
May 2021 Martin Center Program Calendar Our centers are now offering indoor programs. Please carefully read the program description page to learn more about each offering. You MUST register in advance if you wish to participate in any of indoor programs. To register, please email: [email protected] or call FiftyForward Martin Center at 615-376-0102 to sign up. We follow CDC safety guidelines. Sun Mon Tue Wed Thu Fri Sat 1 Beep & Feast 2 3 4 5 6 7 8 9 a.m.-3 p.m. Card Crusad- 9-11 a.m. Community Chat/ Remembering the 7 a.m. Early Bird ers Portal Help Badges Blood Drive/Am Walking Club No 10 a.m. Exercise 9:30 a.m.-12:00 p.m. Scrabble Red Cross 9:30 a.m.-12 p.m. In-Center 10:30 a.m. Intro to Euchre 10 a.m.-12 p.m. Billiards 9 a.m.-12 p.m. Bridge Canasta Program- 10:30 a.m. Poker 12-3 p.m. Games 9 a.m.-3 p.m. Card 10 a.m.-noon Billiards ming 1 p.m. BINGO 1 p.m. Line Dancing Crusaders 10 a.m.-12 p.m. Yarn Art 1 p.m. Watercolor Class 1-3 p.m. Billiards 10 a.m. Exercise 12:30-3 p.m. Open Art 2-3 p.m. Keeping Your Brain Outdoors 12:30-3 p.m. Canasta Healthy 11:30 a.m. Arthritis class 1-3 p.m. Billiards 12:30-3p.m. Bridge 9 10 11 12 13 14 15 9 a.m.-3 p.m. -

View Annual Report
Financial Highlights (Thousands of Dollars and Shares Except Per Share Data) 2006 2005 2004 2003 2002 For The Year Net revenues $ 3,151,481 3,087,627 2,997,510 3,138,657 2,816,230 Operating profi t $ 376,363 310,521 293,012 344,616 219,291 Net earnings (loss) $ 230,055 212,075 195,977 157,664 (170,674) EBITDA Earnings before cumulative effect of accounting change $ 230,055 212,075 195,977 175,015 75,058 Interest expense $ 27,521 30,537 31,698 52,462 77,499 Income taxes $ 111,419 98,838 64,111 69,049 29,030 Depreciation and amortization $ 146,707 180,132 146,180 164,123 183,838 EBITDA (1) $ 515,702 521,582 437,966 460,649 365,425 Cash provided by operating activities $ 320,647 496,624 358,506 454,155 473,139 Cash utilized by investing activities $ 83,604 120,671 84,967 64,879 62,314 Weighted average number of common shares outstanding Basic 167,100 178,303 176,540 173,748 172,720 Diluted 181,043 197,436 196,048 190,058 185,062 Per Common Share Net earnings before cumulative effect of accounting change Basic $ 1.38 1.19 1.11 1.01 .43 Diluted $ 1.29 1.09 .96 .94 .43 Cash dividends declared $ .48 .36 .24 .12 .12 Shareholders’ equity $ 9.57 9.69 9.25 8.01 6.88 At Year End Shareholders’ equity $ 1,537,890 1,723,476 1,639,724 1,405,240 1,191,366 Total assets $ 3,096,905 3,301,143 3,240,660 3,163,376 3,142,881 Long-term debt, including current portions $ 494,917 528,389 626,822 688,204 1,059,115 Debt to capitalization ratio 25% 24% 28% 34% 48% (1) EBITDA (earnings before interest, taxes, depreciation and amortization) represents net earnings (loss) before cumulative effect of accounting change, excluding interest expense, income taxes, depreciation and amortization. -

The Scrabble Player's Handbook Is Available for Free Download At
The Scrabble Player's Handbook is available for free download at www.scrabbleplayershandbook.com 1 Contents Introduction 3 Meet The Team 5 What's Different About Competitive Scrabble? 10 How To Play Good Scrabble 11 The Words 14 What Is Scrabble? 16 Scoring Well 21 Understanding Rack Leaves 32 Word Learning 35 The First Move 46 Tile Tracking 50 Time Management 54 Exchanging 58 Phoneys 64 Set-Ups 65 Open and Closed Boards 68 The Endgame 75 Playing Style 85 How To Play Amazing Scrabble 94 The Luck Element 98 The Game Behind The Game 99 Starting Out in Competitive Play 101 Quackle 103 Zyzzyva 109 Internet Scrabble Club 115 Aerolith 117 Scrabble by Phone 119 Books 121 Scrabble Variants 123 Scrabble Around The World 125 Playing Equipment 127 Glossary 128 Appendix 133 Rules Governing Word Inclusion 133 Two-letter words 137 Three-letter words 140 SCRABBLE® is a registered trademark. All intellectual property rights in and to the game are owned in the U.S.A. by Hasbro Inc., in Canada by Hasbro Canada Inc. and throughout the rest of the world by J.W. Spear & Sons Ltd. of Maidenhead SL6 4UB, England, a subsidiary of Mattel Inc. Mattel and Spear are not affiliated with Hasbro or Hasbro Canada. The Scrabble Player's Handbook is available free of charge. There is no copyright on the contents and readers are encouraged to distribute the book in PDF or printed form to all who would benefit from it. Please respect our work by retaining the footer on every page and by refraining from reproducing any part of this book for financial gain. -

Spin the Wheel. Now That the Christmas Vacation Is Coming Up, We Will Probably Play Some Board(1) Games in the Evenings
Spin The Wheel. Now that the Christmas vacation is coming up, we will probably play some board(1) games in the evenings. We have so many of them! There is a big collection of them, stuffed(2) into a closet in the lounge. Monopoly, Axis and Allies, and Scrabble are three of the more well known ones. My favorite is probably Monopoly; I love games that lead you along a path to a destination, with question cards, and unexpected(3) opportunities or problems along the way. I was actually playing a similar game this morning on the computer, except it wasn't(4) about buying streets or buildings. It was an information game created by a company that deals with retirement. I'm not close to retiring, in fact, I'm probably still about twenty years away from it(5). But the reason I was playing the game, was to try a win the 1st place prize of $50,000. I probably don't stand a chance of(6) winning, but you know, the game turned out to be very interesting. You had to spin a wheel, walk up to 5 steps along the path, and then answer questions, or read and watch informational video clips. The whole point is to get educated about retirement, health, finances, and volunteering. It was an interesting, casual(7) way to learn a lot about retiring. What I realized is that I don't know very much about retiring. One of the aims of this organization is to get retired people involved in the community, to keep them socially healthy. -

30 Minutes Aggravation 2-6 Players Ages 6+ Playing Time
7 Wonders 2-7 players Ages 10+ Playing Time: 30 minutes Aggravation 2-6 players Ages 6+ Playing Time: 45 minutes Agricola 1-5 players Ages 12+ Playing Time: 30 minutes–1.5hours Apples to Apples 4-10 players Ages 10+ Playing Time: 30 minutes Apples to Apples Junior 4-8 players Ages 9+ Playing Time: 30 minutes Arkham Horror 1-8 players Ages 12+ Playing Time: 2-4 hours Axis & Allies Europe 2-4 players Ages 12+ Playing Time: 3.5 hours Axis & Allies 2-5 players Ages 12+ Playing Time: 3 hours Backgammon 2 players Ages 8+ Playing Time: 30 minutes BANG! 4-7 players Ages 8+ Playing Time: 20-40 minutes Battle Cry 2 players Ages 10+ Playing Time: 45 minutes Battleship 2 players Ages 8+ Playing Time: 30 minutes Betrayal at House on the Hill 3-6 players Ages 12+ Playing Time: 1 hour Blokus 2-4 players Ages 5+ Playing Time: 20 minutes Bohnanza 2-7 players Ages 13+ Playing Time: 45 minutes Boss Monster 2-4 players Ages 13+ Playing Time: 20 minutes Candy Land 2-4 players Ages 3+ Playing Time: 30 minutes Carcassonne 2-5 players Ages 8+ Playing Time: 30-40 minutes Caverna: The Cave Farmers 1-7 players Ages 12+ Playing Time: 30 minutes-3.5 hours Checkers 2 players Ages 6+ Playing Time: 30 minutes Chess 2 players Ages 6+ Playing Time: 1 hour Chutes & Ladders 2-6 players Ages 3+ Playing Time: 30 minutes Clue 3-6 players Ages 8+ Playing Time: 45 minutes Clumsy Thief 2-6 players Ages 8+ Playing Time: 15 minutes Codenames 2-8+ players Ages 10+ Playing Time: 15 minutes Concept 4-12 players Ages 10+ Playing Time: 40 minutes Connect 4 2 players Ages 6+ Playing -
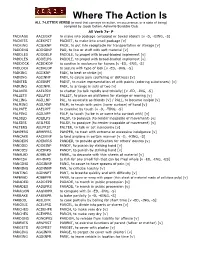
Where the Action Is ALL 7-LETTER VERBS (A Word That Conveys an Action, an Occurrence, Or a State of Being) Compiled by Jacob Cohen, Asheville Scrabble Club
Where The Action Is ALL 7-LETTER VERBS (a word that conveys an action, an occurrence, or a state of being) compiled by Jacob Cohen, Asheville Scrabble Club All Verb 7s- P PACKAGE AACEGKP to make into package (wrapped or boxed object) [v -D, -GING, -S] PACKETS ACEKPST PACKET, to make into small package [v] PACKING ACGIKNP PACK, to put into receptacle for transportation or storage [v] PADDING ADDGINP PAD, to line or stuff with soft material [v] PADDLED ADDDELP PADDLE, to propel with broad-bladed implement [v] PADDLES ADDELPS PADDLE, to propel with broad-bladed implement [v] PADDOCK ACDDKOP to confine in enclosure for horses [v -ED, -ING, -S] PADLOCK ACDKLOP to secure with type of lock [v -ED, -ING, -S] PAIKING AGIIKNP PAIK, to beat or strike [v] PAINING AGIINNP PAIN, to cause pain (suffering or distress) [v] PAINTED ADEINPT PAINT, to make representation of with paints (coloring substances) [v] PAIRING AGIINPR PAIR, to arrange in sets of two [v] PALAVER AAELPRV to chatter (to talk rapidly and trivially) [v -ED, -ING, -S] PALLETS AELLPST PALLET, to place on platforms for storage or moving [v] PALLING AGILLNP PAL, to associate as friends [v] / PALL, to become insipid [v] PALMING AGILMNP PALM, to touch with palm (inner surface) of hand [v] PALPATE AAELPPT to examine by touch [v -D, -TING, -S] PALPING AGILNPP PALP, to touch (to be in or come into contact with) [v] PALSIED ADEILPS PALSY, to paralyze (to render incapable of movement) [v] PALSIES AEILPSS PALSY, to paralyze (to render incapable of movement) [v] PALTERS AELPRST PALTER, to talk or -

The Association of Premier Scrabble* Players JOEL SHERMAN WINS
The Association of Premier Scrabble* Players Issue No. 57 NEWSLETTER December 1997 JOEL SHERMAN WINS WORLD TITLE American Joel Sherman is the 1997 World Scrabble Champion. In a battle of New Yorkers, he defeated stand-up comedian Matt Graham 3-1 in the Final. It was a sweet success for Sherman, who had reached the Final in 1995, only to be defeated by Canada's David Boys. One little-known fact about Joel is that he's a member of die APSP! He joined in 1995, when the World Championship was held in London, and has retained his membership ever since. So we can offer our congratulations to one of our own members! For the first two days the tournament had been dominated by the UK team. At one stage, the top four positions were occupied by UK players. But as the pressure mounted the Americans made their move, with Graham winning 13 successive games to secure his place in the Final. The top UK finisher was Mark Nyman in 5th place, with Russell Byers (7th) also achieving a top ten finish. You can read a full report, including Mark's own account of the event, on page 4. ANDY COOK IS NATIONAL CHAMPION The rise of Andy Cook continues unabated. Within three years he's risen from the ranks of the "who's her to become the UK's National Champion. In the Final he defeated Jackie McLeod, 3-0. Andy's winning prize included an expenses-paid trip to Washington DC to watch the World Championship. Not bad for a weekend's Scrabble! The Intermediate title was won by 21-year-old Paul Chadwick, with a magnificent record of 9 wins and 1 tie in his ten games.