DOCSLIB.ORG

What Is Combinatorics? What Is Optimization? Department of Combinatorics and Optimization University of Waterloo, Ontario, Canada

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
What Is Combinatorics? What Is Optimization? Department of Combinatorics and Optimization University of Waterloo, Ontario, Canada What is Combinatorics? What is Optimization? Department of Combinatorics and Optimization University of Waterloo, Ontario, Canada http://www.math.uwaterloo.ca 1. Introduction The department of C&O o¤ers programs in these two areas. These pages tells you a little bit about them. In industry, commerce, govern- ment, indeed in all walks of life, one frequently needs answers to ques- tions concerning operational e¢ciency. Thus an architect may need to know how to lay out a factory ‡oor so that the article being manufac- tured does not have to be moved about too much as it goes from one machine tool to another; the manager of a shipping company needs to plan the itineraries of his ships so as to increase the amount of goods handled, while avoiding costly waiting-around in docks. A telecom- munications engineer may want to know how best to transmit signals so as to minimize the possibility of error on reception. Further exam- ples of problems of this sort are provided by the planning of a railroad time-table to ensure that trains are available as and when needed, the synchronization of tra¢c lights, and many other real-life situations. Formerly such problems would usually be “solved” by imprecise methods giving results that were both unreliable and costly. Today, they are increasingly being subjected to rigid mathematical analysis, designed to provide methods for …nding exact solutions or highly reli- able estimates rather than vague approximations. Combinatorics and optimization provide many of the mathematical tools used for solving such problems. Combinatorics is the mathematics of discretely structured problems. Although its boundaries are not easily de…ned, combinatorics includes the theories of graphs, enumeration, designs and polyhedra. It is a subject which in the past was studied principally for its aesthetic ap- peal. Today’s modern technology with its vital concern for the dis- crete has given combinatorics new challenges and a new seriousness of purpose. In particular, since computers require discrete formula- tions of problems, combinatorics has become indispensable to modern computer science. 1 2 Optimization, or mathematical programming, is the study of maxi- mizing and minimizing functions subject to speci…ed boundary condi- tions or constraints. The functions to be optimized arise in engineer- ing, the physical and management sciences, and in various branches of mathematics. With the emergence of the computer age, optimization experienced a dramatic growth as a mathematical theory, enhancing both combinatorics and classical analysis. In its applications to en- gineering and management science, optimization forms an important part of the discipline of operations research. 2. Major Areas of Combinatorics and Optimization 2.1. Enumeration. Enumeration is concerned with determining the number of structures with prescribed properties, and is a frequently used tool in mathematics. Many enumeration problems arise from ranking and signi…cance testing in statistics, from probability theory, from telephone networks and from mathematics itself. Extensive cal- culations are often necessary, and the …eld of computational enumera- tion is an important one. The task of getting a computer to evaluate formulae obtained by applying enumerative methods is one requiring considerable experience both with computers and with combinatorics. 2.2. Combinatorial Designs. The study of designs deals with a very important and central problem of combinatorial theory, that of arrang- ing objects into patterns according to speci…ed rules. The principal mathematical tools employed are graph theory, number theory and linear and abstract algebra. The construction of magic squares is an example of a design problem, and before the start of the nineteenth century such problems were mainly of recreational interest. In more recent times the concept of a geometry involving only …nitely many points has been developed, generalized, and built into the elegant and useful theory of combinatorial designs. Today this area embodies the mathematical tools of such applied areas as the design of experiments, tournament scheduling, information retrieval and coding theory. 2.3. Graph Theory. Based upon the simple idea of points intercon- nected by lines, graph theory combines these basic ingredients into a rich and useful theory, which provides powerful tools for constructing models and solving problems concerning discrete arrangements of ob- jects. Technology today poses a great number of problems that require the construction of complex systems through speci…c arrangements of their components. These include problems in the scheduling of indus- trial processes, communication systems, electrical networks, organic- chemical identi…cation, economics and numerous other applied areas. 3 2.4. Linear Programming. Mathematical programming deals with the problem of determining optimal allocations of limited resources to meet given objectives. The resources may correspond to people, mate- rials, money, land or simply to abstract numerical quantities. Out of all permissible allocations of the resources, it is desired to …nd the one or ones which maximize or minimize some numerical quantity such as pro…t or cost. Linear programming deals with that class of program- ming problems for which the function to be optimized is linear and all relations among the variables corresponding to resources are linear. This problem was …rst formulated and solved in the late 1940s. Rarely has a new mathematical technique found such a wide range of practical applications and simultaneously received so thorough a theoretical development in such a short period of time. Today, this theory is being successfully applied to problems of capital budgeting, design of diets, conservation of resources, games of strategy, economic growth prediction and transportation systems. In very recent times linear programming theory has also helped resolve and unify many outstanding problems in combinatorics. 2.5. Nonlinear Optimization. Linear programming has proved an extremely powerful tool, both in modeling real-world problems and as a widely applicable mathematical theory. However, many interest- ing optimization problems are nonlinear. The study of such problems involves a diverse blend of linear algebra, multivariate calculus, numeri- cal analysis and computing techniques. Important special areas include the design of computational algorithms (including interior point tech- niques for linear programing), the geometry and analysis of convex sets and functions, and the study of specially structured problems such as quadratic programming. Nonlinear optimization provides fundamental insights into mathematical analysis, and is widely used in the applied sciences, in areas such as engineering design, regression analysis, inven- tory control, and geophysical exploration amont others. 2.6. Operations Research. The term Operations Research (OR for short) arose in the 1940’s when research was carried out on the design and analysis of mathematical models for military operations. Since that time the scope of OR has expanded to include economic, marketing and corporate planning problems. The growing complexity of management has necessitated the development of sophisticated mathematical tech- niques for planning and decision-making, and OR features prominently in this decision-making process by providing a quantitative evaluation of alternative policies, plans and decisions. The mathematical disci- plines most widely used in OR include mathematical programming, 4 probability and statistics, and computer science. Some areas of OR, such as inventory and production control, and scheduling theory, have grown into subdisciplines in their own right and have become largely indispensable in the modern world. 2.7. Combinatorial Optimization. Packing, covering and partition- ing, which are examples of integer programming problems, are the prin- cipal mathematical topics in the interface between combinatorics and optimization. Combinatorial optimization is the study of these prob- lems. It deals with the classi…cation of integer programming problems according to the complexity of known algorithms for solving them and with the design of good algorithms for solving special subclasses of them. In particular, problems of network ‡ows, matchings and their matroid generalizations are studied. This subject is one of the unify- ing elements of combinatorics, optimization, operations research and computer science. 3. Degree Programs The C&O Department isthehomeoftwoMajorprograms,theC&O Program and the OR Program, each leading to an Honours Bachelor of Mathematics degree. The curricula of these programs are especially appropriate for those showing special talent and interest in modern mathematics and who anticipate graduate studies in mathematics, op- erations research or computer science. The programs have been de- signed to achieve a balance between a strong core of third-year studies in algebra, analysis, combinatorics, and optimization, and more ad- vanced fourth-year studies in at least some of these areas. Students in the C&O Program are encouraged to broaden their mathematical backgrounds further by taking additional third and fourth year courses from at least one of the other four departments..
Load more

Recommended publications
  • FUNDAMENTALS of COMPUTING (2019-20) COURSE CODE: 5023 502800CH (Grade 7 for ½ High School Credit) 502900CH (Grade 8 for ½ High School Credit)
    EXPLORING COMPUTER SCIENCE NEW NAME: FUNDAMENTALS OF COMPUTING (2019-20) COURSE CODE: 5023 502800CH (grade 7 for ½ high school credit) 502900CH (grade 8 for ½ high school credit) COURSE DESCRIPTION: Fundamentals of Computing is designed to introduce students to the field of computer science through an exploration of engaging and accessible topics. Through creativity and innovation, students will use critical thinking and problem solving skills to implement projects that are relevant to students’ lives. They will create a variety of computing artifacts while collaborating in teams. Students will gain a fundamental understanding of the history and operation of computers, programming, and web design. Students will also be introduced to computing careers and will examine societal and ethical issues of computing. OBJECTIVE: Given the necessary equipment, software, supplies, and facilities, the student will be able to successfully complete the following core standards for courses that grant one unit of credit. RECOMMENDED GRADE LEVELS: 9-12 (Preference 9-10) COURSE CREDIT: 1 unit (120 hours) COMPUTER REQUIREMENTS: One computer per student with Internet access RESOURCES: See attached Resource List A. SAFETY Effective professionals know the academic subject matter, including safety as required for proficiency within their area. They will use this knowledge as needed in their role. The following accountability criteria are considered essential for students in any program of study. 1. Review school safety policies and procedures. 2. Review classroom safety rules and procedures. 3. Review safety procedures for using equipment in the classroom. 4. Identify major causes of work-related accidents in office environments. 5. Demonstrate safety skills in an office/work environment.
    [Show full text]
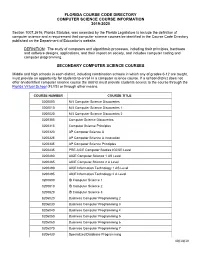
  • Florida Course Code Directory Computer Science Course Information 2019-2020
    FLORIDA COURSE CODE DIRECTORY COMPUTER SCIENCE COURSE INFORMATION 2019-2020 Section 1007.2616, Florida Statutes, was amended by the Florida Legislature to include the definition of computer science and a requirement that computer science courses be identified in the Course Code Directory published on the Department of Education’s website. DEFINITION: The study of computers and algorithmic processes, including their principles, hardware and software designs, applications, and their impact on society, and includes computer coding and computer programming. SECONDARY COMPUTER SCIENCE COURSES Middle and high schools in each district, including combination schools in which any of grades 6-12 are taught, must provide an opportunity for students to enroll in a computer science course. If a school district does not offer an identified computer science course the district must provide students access to the course through the Florida Virtual School (FLVS) or through other means. COURSE NUMBER COURSE TITLE 0200000 M/J Computer Science Discoveries 0200010 M/J Computer Science Discoveries 1 0200020 M/J Computer Science Discoveries 2 0200305 Computer Science Discoveries 0200315 Computer Science Principles 0200320 AP Computer Science A 0200325 AP Computer Science A Innovation 0200335 AP Computer Science Principles 0200435 PRE-AICE Computer Studies IGCSE Level 0200480 AICE Computer Science 1 AS Level 0200485 AICE Computer Science 2 A Level 0200490 AICE Information Technology 1 AS Level 0200495 AICE Information Technology 2 A Level 0200800 IB Computer
    [Show full text]
  • Safety and Security Challenge
    SAFETY AND SECURITY CHALLENGE TOP SUPERCOMPUTERS IN THE WORLD - FEATURING TWO of DOE’S!! Summary: The U.S. Department of Energy (DOE) plays a very special role in In fields where scientists deal with issues from disaster relief to the keeping you safe. DOE has two supercomputers in the top ten supercomputers in electric grid, simulations provide real-time situational awareness to the whole world. Titan is the name of the supercomputer at the Oak Ridge inform decisions. DOE supercomputers have helped the Federal National Laboratory (ORNL) in Oak Ridge, Tennessee. Sequoia is the name of Bureau of Investigation find criminals, and the Department of the supercomputer at Lawrence Livermore National Laboratory (LLNL) in Defense assess terrorist threats. Currently, ORNL is building a Livermore, California. How do supercomputers keep us safe and what makes computing infrastructure to help the Centers for Medicare and them in the Top Ten in the world? Medicaid Services combat fraud. An important focus lab-wide is managing the tsunamis of data generated by supercomputers and facilities like ORNL’s Spallation Neutron Source. In terms of national security, ORNL plays an important role in national and global security due to its expertise in advanced materials, nuclear science, supercomputing and other scientific specialties. Discovery and innovation in these areas are essential for protecting US citizens and advancing national and global security priorities. Titan Supercomputer at Oak Ridge National Laboratory Background: ORNL is using computing to tackle national challenges such as safe nuclear energy systems and running simulations for lower costs for vehicle Lawrence Livermore's Sequoia ranked No.
    [Show full text]
  • A Logical Approach to Asymptotic Combinatorics I. First Order Properties
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector ADVANCES IN MATI-EMATlCS 65, 65-96 (1987) A Logical Approach to Asymptotic Combinatorics I. First Order Properties KEVIN J. COMPTON ’ Wesleyan University, Middletown, Connecticut 06457 INTRODUCTION We shall present a general framework for dealing with an extensive set of problems from asymptotic combinatorics; this framework provides methods for determining the probability that a large, finite structure, ran- domly chosen from a given class, will have a given property. Our main concern is the asymptotic probability: the limiting value as the size of the structure increases. For example, a common problem in elementary probability texts is to show that the asymptotic probabity that a per- mutation will have no fixed point is l/e. We shall say nothing about the closely related problem of determining rates of convergence, although the methods presented here may extend to such problems. To develop a general approach we must fix a language for specifying properties of structures. Thus, our approach is logical; logic is the branch of mathematics that deals with problems of language. In this paper we con- sider properties expressible in the language of first order logic and speak of probabilities of first order sentences rather than properties. In the sequel to this paper we consider properties expressible in the more general language of monadic second order logic. Clearly, we must restrict the classes of structures we consider in order for questions about asymptotic probabilities to be meaningful and significant. Therefore, we choose to consider only classes closed under disjoint unions and components (see Sect.
    [Show full text]
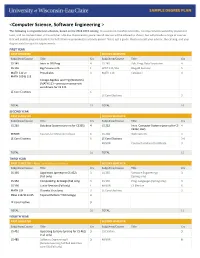
  • <Computer Science, Software Engineering >
    <Computer Science, Software Engineering > The following is a hypothetical schedule, based on the 2018-2019 catalog. It assumes no transferred credits, no requirements waived by placement tests, and no courses taken in the summer. UW-Eau Claire cannot guarantee all courses will be offered as shown, but will provide a range of courses that will enable prepared students to fulfill their requirements in a timely period. This is just a guide. Please consult your advisor, the catalog, and your degree audit for specific requirements. FIRST YEAR FIRST SEMESTER SECOND SEMESTER Subj/Area/Course Title Crs Subj/Area/Course Title Crs CS 145 Intro to OO Prog 4 CS 245 Adv. Prog. Data Structures 4 CS 146 Big Picture in CS 1 WRIT 114/116 Blugold Seminar 5 MATH 112 or Precalculus 4 MATH 114 Calculus I 4 MATH 109 & 113 College Algebra and Trig (Winterim) (MATH 113 – prereq or concurrent enrollment for CS 245 LE Core Electives 6 LE Core Electives 3 TOTAL 15 TOTAL 16 SECOND YEAR FIRST SEMESTER SECOND SEMESTER Subj/Area/Course Title Crs Subj/Area/Course Title Crs CS 260 Database Systems (prereq for CS355) 4 CS 252 Intro. Computer Systems (prereq for CS 4 CS352, 452) MINOR Courses for Minor/Certificate 6 CS 268 Web Systems 3 LE Core Electives 6 LE Core Electives 3-6 MINOR Courses for Minor/Certificate 3 TOTAL 16 TOTAL 15 THIRD YEAR FIRST SEMESTER – Apply for Admission to Major SECOND SEMESTER Subj/Area/Course Title Crs Subj/Area/Course Title Crs CS 335 Algorithms (prereq for CS 452) 3 CS 355 Software Engineering I 3 (Fall only) (Spring only) CS 352 ComputeOrg.
    [Show full text]
  • Interactions of Computational Complexity Theory and Mathematics
    Interactions of Computational Complexity Theory and Mathematics Avi Wigderson October 22, 2017 Abstract [This paper is a (self contained) chapter in a new book on computational complexity theory, called Mathematics and Computation, whose draft is available at https://www.math.ias.edu/avi/book]. We survey some concrete interaction areas between computational complexity theory and different fields of mathematics. We hope to demonstrate here that hardly any area of modern mathematics is untouched by the computational connection (which in some cases is completely natural and in others may seem quite surprising). In my view, the breadth, depth, beauty and novelty of these connections is inspiring, and speaks to a great potential of future interactions (which indeed, are quickly expanding). We aim for variety. We give short, simple descriptions (without proofs or much technical detail) of ideas, motivations, results and connections; this will hopefully entice the reader to dig deeper. Each vignette focuses only on a single topic within a large mathematical filed. We cover the following: • Number Theory: Primality testing • Combinatorial Geometry: Point-line incidences • Operator Theory: The Kadison-Singer problem • Metric Geometry: Distortion of embeddings • Group Theory: Generation and random generation • Statistical Physics: Monte-Carlo Markov chains • Analysis and Probability: Noise stability • Lattice Theory: Short vectors • Invariant Theory: Actions on matrix tuples 1 1 introduction The Theory of Computation (ToC) lays out the mathematical foundations of computer science. I am often asked if ToC is a branch of Mathematics, or of Computer Science. The answer is easy: it is clearly both (and in fact, much more). Ever since Turing's 1936 definition of the Turing machine, we have had a formal mathematical model of computation that enables the rigorous mathematical study of computational tasks, algorithms to solve them, and the resources these require.
    [Show full text]
  • Middleware and Application Management Architecture
    Middleware and Application Management Architecture vorgelegt vom Diplom-Informatiker Sven van der Meer aus Berlin von der Fakultät IV – Elektrotechnik und Informatik der Technischen Universität Berlin zur Erlangung des akademischen Grades Doktor der Ingenieurwissenschaften - Dr.-Ing. - genehmigte Dissertation Promotionsausschuss: Vorsitzender: Prof. Gorlatch Berichter: Prof. Dr. Dr. h.c. Radu Popescu-Zeletin Berichter: Prof. Dr. Kurt Geihs Tag der wissenschaftlichen Aussprache: 25.09.2002 Berlin 2002 D 83 Middleware and Application Management Architecture Sven van der Meer Berlin 2002 Preface Abstract This thesis describes a new approach for the integrated management of distributed networks, services, and applications. The main objective of this approach is the realization of software, systems, and services that address composability, scalability, reliability, and robustness as well as autonomous self-adaptation. It focuses on middleware for management, control, and use of fully distributed resources. The term integra- tion refers to the task of unifying existing instrumentations for middleware and management, not their replacement. The rationale of this work stems from the fact, that the current situation of middleware and management systems can be described with the term interworking. The actually needed integration of management and middleware concepts is still an open issue. However, identified trends in communications and computing demand for integrated concepts rather than the definition of new interworking scenarios. Distributed applications need to be prepared to be used and operated in a stable, secure, and efficient way. Middleware and service platforms are employed to solve this task. To guarantee this objective for a long-time operation, the systems needs to be controlled, administered, and maintained in its entirety, supporting the general aim of the system, and for each individual component, to ensure that each part of the system functions perfectly.
    [Show full text]
  • An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics
    STUDENT MATHEMATICAL LIBRARY Volume 87 An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics Matthew Katz Jan Reimann Mathematics Advanced Study Semesters 10.1090/stml/087 An Introduction to Ramsey Theory STUDENT MATHEMATICAL LIBRARY Volume 87 An Introduction to Ramsey Theory Fast Functions, Infinity, and Metamathematics Matthew Katz Jan Reimann Mathematics Advanced Study Semesters Editorial Board Satyan L. Devadoss John Stillwell (Chair) Rosa Orellana Serge Tabachnikov 2010 Mathematics Subject Classification. Primary 05D10, 03-01, 03E10, 03B10, 03B25, 03D20, 03H15. Jan Reimann was partially supported by NSF Grant DMS-1201263. For additional information and updates on this book, visit www.ams.org/bookpages/stml-87 Library of Congress Cataloging-in-Publication Data Names: Katz, Matthew, 1986– author. | Reimann, Jan, 1971– author. | Pennsylvania State University. Mathematics Advanced Study Semesters. Title: An introduction to Ramsey theory: Fast functions, infinity, and metamathemat- ics / Matthew Katz, Jan Reimann. Description: Providence, Rhode Island: American Mathematical Society, [2018] | Series: Student mathematical library; 87 | “Mathematics Advanced Study Semesters.” | Includes bibliographical references and index. Identifiers: LCCN 2018024651 | ISBN 9781470442903 (alk. paper) Subjects: LCSH: Ramsey theory. | Combinatorial analysis. | AMS: Combinatorics – Extremal combinatorics – Ramsey theory. msc | Mathematical logic and foundations – Instructional exposition (textbooks, tutorial papers, etc.). msc | Mathematical
    [Show full text]
  • Artificial Intelligence Program 1
    Artificial Intelligence Program 1 Artificial Intelligence Program Reid Simmons, Director of the BSAI program (NSH 3213) 15-122 Principles of Imperative Computation 10 (students without credit or a waiver for 15-112, Jean Harpley, Program Coordinator (NSH 1517) Fundamentals of Programming and Computer www.cs.cmu.edu/bs-in-artificial-intelligence (http://www.cs.cmu.edu/bs-in- Science, must take 15-112 before 15-122) artificial-intelligence/) 15-150 Principles of Functional Programming 10 15-210 Parallel and Sequential Data Structures and 12 Overview Algorithms 15-213 Introduction to Computer Systems 12 Carnegie Mellon University has led the world in artificial intelligence 15-251 Great Ideas in Theoretical Computer Science 12 education and innovation since the field was created. It's only natural, then, that the School of Computer Science would offer the nation's first bachelor's degree in Artificial Intelligence, which started in Fall 2018. Artificial Intelligence The new BSAI program gives students the in-depth knowledge needed to transform large amounts of data into actionable decisions. The program All of the following three AI core courses: Units and its curriculum focus on how complex inputs — such as vision, language 07-180 Concepts in Artificial Intelligence 5 and huge databases — can be used to make decisions or enhance human 15-281 Artificial Intelligence: Representation and 12 capabilities. The curriculum includes coursework in computer science, Problem Solving math, statistics, computational modeling, machine learning and symbolic computation. Because Carnegie Mellon is devoted to AI for social good, 10-315 Introduction to Machine Learning (SCS Majors) 12 students will also take courses in ethics and social responsibility, with the plus one of the following AI core courses: option to participate in independent study projects that change the world for 16-385 Computer Vision 12 the better — in areas like healthcare, transportation and education.
    [Show full text]
  • Applications and Combinatorics in Algebraic Geometry Frank Sottile Summary
    Applications and Combinatorics in Algebraic Geometry Frank Sottile Summary Algebraic Geometry is a deep and well-established field within pure mathematics that is increasingly finding applications outside of mathematics. These applications in turn are the source of new questions and challenges for the subject. Many applications flow from and contribute to the more combinatorial and computational parts of algebraic geometry, and this often involves real-number or positivity questions. The scientific development of this area devoted to applications of algebraic geometry is facilitated by the sociological development of administrative structures and meetings, and by the development of human resources through the training and education of younger researchers. One goal of this project is to deepen the dialog between algebraic geometry and its appli- cations. This will be accomplished by supporting the research of Sottile in applications of algebraic geometry and in its application-friendly areas of combinatorial and computational algebraic geometry. It will be accomplished in a completely different way by supporting Sottile’s activities as an officer within SIAM and as an organizer of scientific meetings. Yet a third way to accomplish this goal will be through Sottile’s training and mentoring of graduate students, postdocs, and junior collaborators. The intellectual merits of this project include the development of applications of al- gebraic geometry and of combinatorial and combinatorial aspects of algebraic geometry. Specifically, Sottile will work to develop the theory and properties of orbitopes from the perspective of convex algebraic geometry, continue to investigate linear precision in geo- metric modeling, and apply the quantum Schubert calculus to linear systems theory.
    [Show full text]
  • Combinatorics and Graph Theory I (Math 688)
    Combinatorics and Graph Theory I (Math 688). Problems and Solutions. May 17, 2006 PREFACE Most of the problems in this document are the problems suggested as home- work in a graduate course Combinatorics and Graph Theory I (Math 688) taught by me at the University of Delaware in Fall, 2000. Later I added several more problems and solutions. Most of the solutions were prepared by me, but some are based on the ones given by students from the class, and from subsequent classes. I tried to acknowledge all those, and I apologize in advance if I missed someone. The course focused on Enumeration and Matching Theory. Many problems related to enumeration are taken from a 1984-85 course given by Herbert S. Wilf at the University of Pennsylvania. I would like to thank all students who took the course. Their friendly criti- cism and questions motivated some of the problems. I am especially thankful to Frank Fiedler and David Kravitz. To Frank – for sharing with me LaTeX files of his solutions and allowing me to use them. I did it several times. To David – for the technical help with the preparation of this version. Hopefully all solutions included in this document are correct, but the whole set is by no means polished. I will appreciate all comments. Please send them to [email protected]. – Felix Lazebnik 1 Problem 1. In how many 4–digit numbers abcd (a, b, c, d are the digits, a 6= 0) (i) a < b < c < d? (ii) a > b > c > d? Solution. (i) Notice that there exists a bijection between the set of our numbers and the set of all 4–subsets of the set {1, 2,..., 9}.
    [Show full text]
  • Combinatorics: a First Encounter
    Combinatorics: a first encounter Darij Grinberg Thursday 10th January, 2019at 9:29pm (unfinished draft!) Contents 1. Preface1 1.1. Acknowledgments . .4 2. What is combinatorics?4 2.1. Notations and conventions . .4 1. Preface These notes (which are work in progress and will remain so for the foreseeable fu- ture) are meant as an introduction to combinatorics – the mathematical discipline that studies finite sets (roughly speaking). When finished, they will cover topics such as binomial coefficients, the principles of enumeration, permutations, parti- tions and graphs. The emphasis falls on enumerative combinatorics, meaning the art of computing sizes of finite sets (“counting”), and graph theory. I have tried to keep the presentation as self-contained and elementary as possible. The reader is assumed to be familiar with some basics such as induction proofs, equivalence relations and summation signs, as well as have some experience with mathematical proofs. One of the best places to catch up on these basics and to gain said experience is the MIT lecture notes [LeLeMe16] (particularly their first five chapters). Two other resources to familiarize oneself with proofs are [Hammac15] and [Day16]. Generally, most good books about “reading and writing mathemat- ics” or “introductions to abstract mathematics” should convey these skills, although the extent to which they actually do so may differ. These notes are accompanying two classes on combinatorics (Math 4707 and 4990) I am giving at the University of Minneapolis in Fall 2017. Here is a (subjective and somewhat random) list of recommended texts on the kinds of combinatorics that will be considered in these notes: • Enumerative combinatorics (aka counting): 1 Notes on graph theory (Thursday 10th January, 2019, 9:29pm) page 2 – The very basics of the subject can be found in [LeLeMe16, Chapters 14– 15].
    [Show full text]