MATHEMATICS 100 Name
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Welcome to the Heart of Europe Find out | Invest | Reap the Benefits More Than 2,800 Advertising Boards in 16 German Cities Promoted Erfurt in 2014/2015
Welcome to the heart of Europe Find out | Invest | Reap the benefits More than 2,800 advertising boards in 16 German cities promoted Erfurt in 2014/2015. The confident message of this campaign? Erfurt is growing and continues to develop at a rapid pace. Inhalt Contents A city at the heart of the action. Erfurt is growing 2 In the heart of Germany. Location and transport links 4 A growing city. Projects for the future 6 Reinventing the heart of the city. ICE-City Erfurt 8 On fertile soil. Industry in Erfurt 10 Already bearing fruit. Leading companies 12 A region ready for take-off. The Erfurt economic area 16 A meeting place in the heart of Europe. Conferences and conventions 18 A passion for teaching and research. Campus Thuringia 20 A city to capture your heart. Life in Erfurt 24 Welcome to Erfurt. Advice and contact details 28 | 1 Erfurt is growing A city at the heart of the action. Land area of Erfurt: 269 km2 2 | Erfurt is growing Erfurt is going places! It’s not for nothing that the Cologne Insti- Most of the old town has been restored The many companies that have moved tute for Economic Research named Erfurt and combines medieval charm with the to Erfurt in recent years are making this among the ten most dynamic cities in buzz of an urban centre. possible. Germany in its 2014 rankings. You can see Erfurt, the regional capital of Thuringia, the changes everywhere and sense a spirit is a prime hotspot for development and, ‘Erfurt is growing’ is therefore the confi- of dynamism: all kinds of housing projects as such, offers the many young people who dent message that is currently being heard are being built across the city, new hotels choose to settle here excellent prospects all over Germany. -

Saint Petersburg State University Joint Seed Money Funding Scheme
Call for Proposals 2018 Freie Universität Berlin – Saint Petersburg State University Joint Seed Money Funding Scheme With the goal of facilitating cooperation in the framework of a strategic partnership, Freie Universität Berlin (FUB) and Saint Petersburg State University (SPSU) have established a joint seed money funding scheme. The funding shall enable FUB and SPSU faculty and researchers to identify complementary strengths, facilitate the use of synergies, increase joint research, high level publications, academic mobility, and promote the development of outstanding future research projects. The joint funding scheme with an annual budget of € 40.000 (equivalent in roubles, respectively) aims at supporting the first steps of research collaboration. The following formats are possible: • Intensive research workshops • Short term research stays (for young as well as established researchers) • Research-oriented teaching / short intensive graduate seminars • Mobility for the preparation of joint research proposals The supported activities should have a clearly defined focus and serve as a catalyst for the development of new joint projects. The activities can take place in Berlin or in Saint Petersburg; participants should include both senior and junior faculty/researchers of FUB and SPSU. Maximum funding per proposal is € 10.000 (equivalent in roubles respectively). The motivation for holding the activity should be clearly explained, including how the involved FUB and SPSU institutes or departments can profit long term from this cooperation and what synergies can arise. Inclusion of German non-university research institutions such as Max Planck Institutes, Helmholtz Centers, and others as well as Russian institutions, is encouraged, however, the additional costs must be covered by these partners themselves. -

Igor Petrovic Film Music Composer & SFX
Igor Petrovic Film Music Composer & SFX Profile Details My interests concern both audio and visual techniques. Whilst I was studying at Berlin, Germany, 15157581095 dBs Music Berlin, I volunteered in numerous exhibitions and have performed at [email protected] many up and coming venues around Berlin. In 2015, I was even part of one of the c.net biggest festivals in Europe - Exit Festival 2015, in Novi Sad. Date of birth I am a competent sound technician, sound engineer, music composer, mixing 01.12.1996 and mastering engineer, working both with soware and hardware - complete understanding of a subject is unavoidable for me. For the past 5 years I have fine Nationality tuned my skills in design, social media pages design, newsletter design, website Serbian and community platform creation, and both 2D and 3D animation. Links Employment History www.igorpetrovic.squarespace.c om Graphic Designer at Visual Meta, Berlin, Germany 2018 – 2019 Skills Please find letter of recommendation on my website. Film Scoring Consultant at Petro Art Production D.O.O, Berlin Sound Design 2019 Theme Parks & Entertainment Industry Consultant. Please find the letter of Sound Editing recommendation on my website. Music Arrangement Education Mixing & Mastering Primary School, Mladost, Vrsac, Serbia Surround Sound Mixing 2003 – 2011 Field Recording High School, Indian International School, Salalah, Oman 2011 – 2013 Nuendo & Cuebase High School, Gimnasimum Borislav Petrov Braca, Vrsac, Serbia Ableton Live 2013 – 2014 Pro Tools Graduate High School, Gymnasium Zivorad Jankovic, NoviSad, Serbia Adobe Photoshop 2014 – 2015 Sound Engineering, Hertz Studio, Novi Sad, Serbia Languages 2015 – 2016 Serbian During this time I was also in Dubai. -

Calibration of Artificial Athlete Berlin/Stuttgart Summary Of
Calibration of Artificial Athlete Berlin/Stuttgart Summary of Calibration Series Performed in 2000 1. Introduction and Rational The Artificial Athletes Berlin and Stuttgart were developed by the FMPA Stuttgart (Otto-Graf- Institut) of the University of Stuttgart around 1970. The tests, which are specified in the German standards DIN 18035-6 "Sports Grounds; Synthetic Surfaced Areas" and DIN 18032-2 "Sports Halls; Sports Surfaces – Requirements, Testing, Maintenance",. and have been adopted by various national and international bodies (FIH, IAAF, ASTM, ITF, CEN, FIFA, UEFA). Over the years, especially the past 10 years, modifications to these DIN standards have taken place, which were at times inconsistent, resulting in major questions and concerns regarding the proper design of the test apparatus, the test procedure, the evaluation of measurements and the accuracy of the test results. The IAAF Accredited Labs of the ISSS felt that the resolution of these uncertainties was crucial and, based on the lack of response by the DIN (Deutsches Institut für Normung = German Institute of Standardization) to professional advice, took the initiative themselves to clarify the problems involved. As a first step, the ISSS called for papers analysing the structure of the Artificial Athletes and providing solutions for the pending problems. The submitted papers were received from Mark Harrison (GB), Dr. Konrad Binder (A), Dr. John Dunlop (AU) and Hans J. Kolitzus (D). The papers were published on ISSS's website www.isss.de. In a meeting held in Le Mans (F) in September 1999, the papers and problems were discussed in depth and a unanimous resolution was passed covering all open problems. -

Presentación De Powerpoint
EUROVELO PILGRIMS ROUTE: DISCOVER GALICIA BY BIKE THE PILGRIMAGE TO SANTIAGO IN 2018 327,400 OFFICIAL ACCREDITATIONS EUROVELO IN SPAIN +/- 4,000KM DEVELOPMENT OF CYCLE TOURISM IN GALICIA THROUGH THE EUROVELO PROJECT EuroVelo R3 “Pilgrims’ Route” _ 196 km established route between Pefrafita do Cebreiro and Santiago de Compostela. (2019) _ 91 km proposed route awaiting approval between Santiago de Compostela and Finisterre-Muxía. (2019-2021) Finisterre/ Muxía EUROVELO PILGRIMS’ ROUTE _ 196km in length / +3.622 metres elevation _3 proposed stages or sections: Pedrafita-Sarria / Sarria-Melide / Melide-Santiago de Compostela EUROVELO PILGRIMS’ ROUTE _ Respects the pilgrim spirit of the Way of Saint James. _ It enables visits to the main places of interest along the French Way, which connects Pedrafita do Cebreiro and Santiago de Compostela. _Wide range of accommodation and maintenance services. UNIQUE SITES _Regular contact with small towns and charming places along the designed route. The pilgrim spirit can be experienced throughout our cycle route. Photo: _Pedrafita do Cebreiro is a prehistoric village located at 1,300 metres above sea level, between the mountains of O Courel and Os Ancares. LANDSCAPES _Galicia is a region with great natural wealth. The R3 Pilgrims’ Route offers spectacular scenery through local, very quiet roads with hardly any traffic. Photo: _ Cyclists with the Sierra de O Courel in the background. HERITAGE _ Along the route you can visit several examples of the French Way’s cultural heritage. The most representative is the final destination, the Cathedral of Santiago de Compostela. Photo: _A stop on our trip to visit the Monastery of Samos. -

Berlin and the East of Germany
Berlin and the East of Germany Monarchs, Poets and Reformers (Private Tour) For more than three centuries the rulers of Brandenburg commissioned the best artists of their time to enhance the Royal residences in and around Berlin with elaborate palaces and gardens. There was building activity under a long series of Prussian monarchs – from Joachim II to the Great Elector, and from Frederick the Great to the last of the German emperors, William II. Visit the resulting works of architecture and landscape gardening, which are overwhelming. Also visit the stunningly beautiful cities of Leipzig and Dresden in Saxony with their rich cultural heritage, follow Martin Luther’s footsteps in Wittenberg, Wartburg and Erfurt, visit Weimar, the town of poets and thinkers and enjoy its rich history from Luther to the iron curtain – and its opening! Map ⚫ Destinations ⚫ Hamburg Overnights ⚫ Other Cities NETHER- LANDS GERMANY POLAND Berlin Hanover ⚫ Potsdam ⚫ Lutherstadt Wittenberg ⚫ ⚫ Leipzig Erfurt Dresden ⚫ ⚫ Cologne Eisenach ⚫ Weimar CZECH REPUBLIC Itinerary Day 1 – DEPARTURE Board your flight from home to Berlin. This itinerary assumes this to be an overnight flight. Air fare independently arranged. Berlin and the East of Germany – Monarchs, Poets and Reformers 2 Day 2 – WELCOME TO BERLIN Arrival in Berlin, the German Capital. The transfers to the hotel depart at 10 a.m. and at 1 p.m. Rest in the afternoon and take advantage of the hotel facilities, or to go for a first stroll in the city. Tonight you'll meet your travelling companions and tour director and enjoy a great welcome dinner. > Your tour includes: Transfer from airport to hotel, dinner, hotel in Berlin Day 3 – BERLIN SIGHTSEEING, CHARLOTTENBURG PALACE Start your day with an orientation tour of the capital of Germany. -

Sunopta to Demand Immediate Delisting from Berlin-Bremen Stock Exchange
SunOpta to Demand Immediate Delisting from Berlin-Bremen Stock Exchange TORONTO--Aug. 5, 2004--SunOpta Inc. (SunOpta or the Company) (Nasdaq:STKL) (TSX:SOY) today announced that it is demanding an immediate delisting from the Berlin-Bremen Stock Exchange in an attempt to prevent trading practices that are banned in the United States. SunOpta recently learned that it was one of more than 200 companies added to the Berlin- Bremen Stock Exchange without its knowledge, consent or authorization. Media reports concerning other companies have indicated that some stock traders may attempt to use this exchange to manipulate stock prices. SunOpta's management has instructed its counsel to request the immediate removal of SunOpta's common stock from this exchange. "We have no interest in trading on any exchange on which we have not sought listing," said Jeremy N. Kendall, SunOpta's Chairman & Chief Executive Officer. SunOpta Inc. is an owner/operator of high-growth ethical businesses, focusing on integrated business models in the natural and organic food markets. For the last six consecutive years, SunOpta was included in Profit magazine's 'Profit 100' list of the 100 fastest growing companies in Canada. The company has three business units: the SunOpta Food Group, which specializes in sourcing, processing and distribution of natural and organic food products integrated from seed through packaged products; the Opta Minerals Group, a producer, distributor, and recycler of environmentally friendly industrial materials; and the StakeTech Steam Explosion Group that engineers and markets clean pulping systems using patented steam explosion technology. Each of these business units has proprietary products and services that give it a solid competitive advantage in its sector. -

Hamburg, Berlin, Dresden – Germany 2021
Hamburg, Berlin, Dresden – Germany 2021 Hamburg, Berlin, Dresden – 13 days Departure: April 30, 2021 Return: May 12, 2021 In Hamburg, on May 2nd the Concert of Beethoven’s 5th Symphony and other works at the Elbphilharmonic Hall conducted by Kent Nagano. On May 4th opera Der Freischutz by Carl Maria von Weber, is conducted by Kent Nagano, with Eric Cutler singing as Max, Jacquelyn Wagner as Agathe, Narea as Annchen, Bernhard Hansky as Ottokar, and the Philharmonisches Staatsorchester Hamburg. We stay at the super deluxe Fairmont Four Seasons Hotel on the Alster lake in Hamburg, close to fine museums. In Berlin, on May 6th the opera La Traviata by Verdi, is conducted by Eun Sun Kim, who has been named the Caroline H. Hume Music Director Designate of San Francisco Opera. Elsa Dreisig singing as Violetta Valery, Freddie De Tommaso as Alfredo Germont, George Petean as Giorgio Germont, and Natalia Shrycka as Flora at Staatsoper Unter den Linden. On May 7th, the opera Salome by Richard Strauss, will be conducted by Thomas Guggeis, with John Daszak singing as Herodes, Waltraud Meier as Herodias, Vida Mikneviciute as Salome, and Johan Reuter as Jochanaan at Staatsoper Unter den Linden. In Dresden, on May 9th, the opera Don Carlos by Verdi, is conducted by Paolo Arrivabeni, with René Pape singing as Filippo II, Hibla Gerzmava as Elisabetta di Valois, Tomislav Mužek as Don Carlos, and Elena Maximova as La principessa Eboli at Semperoper. Opera Performances In Hamburg: May 2 – Concert of Beethoven’s 5th Symphony and other works at the Elbphilharmonic Hall conducted by Kent Nagano. -

Paris | London
Galerie Max Hetzler Berlin | Paris | London Giulia Andreani Was birgst du so bang dein Gesicht? maxhetzler.com Online Exhibition Galerie Max Hetzler Berlin | Paris | London “Faced with strange scenes, and goaded on by curiosity, the viewer sets out in search of clues that they will not always find. For as they know, enigmas are at play beneath seemingly harmless, unremarkable appearances – battles that may be violent or silent, visible or imperceptible, but always both private and political.” – Jean-Marie Gallais Giulia Andreani (b. 1985) repurposes personal memorabilia and archival photographs through painting to address forgotten histories, often through a feminist lens. Recalling the collage of Max Ernst and Hannah Höch, the artist uses watercolour and acrylic to reproduce, alter and combine motifs from these photographs generating new layers of meaning. Working primarily in Payne’s Grey, a blue-grey hue at once warm and cold, and a possible nod to Gerhard Richter, Andreani presents figurative work untainted by the artifice and power of painterly colour. The artist also looks to the aesthetics of Italian cinema including Pietro Germi’s tragicomic neorealism, Pier Paolo Pasolini’s hyper- mannerism and Luchino Visconti’s decadent lighting. This exhibition brings together figures as varied as the Little Red Riding Hood, Hitler’s lover, Frida Kahlo and anonymous Italian immigrants, illustrating themes central to Andreani’s practice including women’s position in society, motherhood, trauma and forgotten figures in political and art history. In these intimately-scaled works, purposefully selected by the artist for online viewing, Andreani addresses notions of historical amnesia and unearths buried narratives, specific and universal. -

V Ie Nna , Prague, Berlin & Stockholm
rague, Berlin & M na, P Stockho usic en ig and Wittenberg lm Capi : Vi eipz tals of Europe Tour , L uary 8, 2019 P den ebr lus Visit Dres - F s to Bratislava, y 24 Januar The Gustavus Choir Dr. Gregory Aune, Conductor Plans are in the works to form a Gustavus alumni choir which will join The Gustavus Choir and conductor Dr. Gregory Aune on his final international choir tour. The alumni choir will perform select repertoire with The Gustavus Choir during the concert program. Joining the tour as a companion participant (not part of the alumni choir) is also available. Registration for alumni to join this custom travel experience will open in late March 2018. Travel arrangements are being finalized and the estimated cost is $5,600 including an estimated airfare from Minneapolis-St. Paul, 14 nights’ accommodations, transportation and touring, tour manager throughout, local guides and 25 meals. A deposit of $600 is required with registration and final payment is due 75 days prior to departure. Space will be limited, and it is very important to indicate your interest early. To be included on a list to receive further details, please email or call Ann Volk at [email protected] or 507-933-7577. Vienna, Austria This travel experience begins in Austria’s capital city for a three-night stay. Learn about the amazing Hapsburgs and their influence on the arts in Vienna with visits to the Kunsthistoriches Museum and the Imperial Treasury along with sites related to Vienna’s famous composers. Concert performance opportunity at Stephensdom, pending confirmation.* Drive to Prague features a stop in Bratislava. -

European League of Football Stuttgart Surge Vs Berlin Thunder (Jul 04, 2021 at Berlin)
Scoring Summary (Final) ELF - European League of Football Stuttgart Surge vs Berlin Thunder (Jul 04, 2021 at Berlin) Stuttgart Surge (1-2-0) vs. Berlin Thunder (1-1-0) Date: Jul 04, 2021 • Site: Berlin • Stadium: Stadion am Wurfplatz Attendance: 800 Score by Quarters 1 2 3 4 Total Stuttgart Surge 6 8 5 0 19 Berlin Thunder 12 6 6 16 40 Qtr Time Scoring Play V-H 1st 08:15 BT - Seantarius Jones 5 yd pass from Calvin Stitt (Jonas Schenderlein kick failed), 8-68 3:57 0 - 6 05:32 SS - Louis Geyer 34 yd pass from Aaron Ellis (Aaron Ellis kick blockd), 1-34 0:00 6 - 6 02:23 BT - Seantarius Jones 29 yd pass from Calvin Stitt (Jonas Schenderlein kick failed), 5-75 3:00 6 - 12 2nd 10:29 BT - Seantarius Jones 4 yd pass from Calvin Stitt (Calvin Stitt pass failed), 6-69 3:32 6 - 18 01:34 SS - David Meza 10 yd pass from Aaron Ellis (Paul Steigerwald pass from A. Ellis), 8-63 2:55 14 - 18 3rd 14:08 BT - Nicolai Schumann 66 yd pass from Calvin Stitt (Jonas Schenderlein kick blockd), 2-71 0:52 14 - 24 14:08 SS - Ben Wenzler PAT return 16 - 24 03:40 SS - Timo Bronn 29 yd field goal, 6-60 3:12 19 - 24 4th 14:48 BT - Jocques Crawford 43 yd run (Jocques Crawford pass from C. Stitt), 8-68 3:39 19 - 32 05:48 BT - Jocques Crawford 81 yd run (Seantarius Jones pass from C. Stitt), 2-80 1:07 19 - 40 Kickoff time: 15:00 • End of Game: 17:55 • Total elapsed time: 02.55 Officials: Referee: M. -
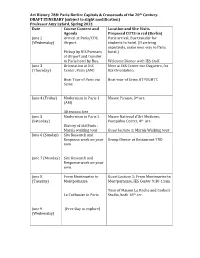
Art History 288: Paris-Berlin: Capitals & Crossroads of the 20Th Century
Art History 288: Paris-Berlin: Capitals & Crossroads of the 20th Century. DRAFT ITINERARY (subject to slight modification) Professor Amy Lyford, Spring 2021 Date Course Content and Location and Site Visits Agenda Proposed CUTS in red (Berlin) June 2 Arrival at Paris/CDG Paris arrival, Bus transfer for (Wednesday) Airport. students to hotel. (If arriving separately, make own way to Paris Pickup by IES Partners hotel.) at Airport and transfer to Paris hotel by Bus. Welcome Dinner with IES Staff. June 3 Orientation at IES Meet at IES Center rue Daguerre, for (Thursday) Center, Paris (AM) IES Orientation. Boat Tour of Paris via Boat tour of Seine AT NIGHT?. Seine. June 4 (Friday) Modernism in Paris 1 Musee Picasso, 3rd arr. (AM) Afternoon free June 5 Modernism in Paris 2 Musee National d’Art Moderne, (Saturday) Pompidou Center, 4th arr. History of old Paris : Marais walking tour Guest lecture 1: Marais Walking tour June 6 (Sunday) Site Research and Response work on your Group Dinner at Restaurant TBD own June 7 (Monday) Site Research and Response work on your own June 8 From Montmartre to Guest Lecture 2: From Montmartre to (Tuesday) Montparnasse Montparnasse, IES Center 9:30-11am Tour of Maison La Roche and Corbu’s Le Corbusier in Paris Studio, both 16th arr. June 9 (Free Day to explore) (Wednesday) Art History 288: Paris-Berlin: Capitals & Crossroads of the 20th Century. DRAFT ITINERARY (subject to slight modification) Professor Amy Lyford, Spring 2021 June 10 Paris in the late 1930s: Palais de Tokyo/Trocadero, 16th arr. (Thursday) From the International Exposition to the Shoah Memorial Visit, 4th arr.