Dynamical System Analysis of Logotropic Dark Fluid with a Power
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Panihati Mahavidyalaya
Panihati Mahavidyalaya Kolkata An exclusive Guide by Panihati Mahavidyalaya Courses & Fees 2021 Showing 19 Courses Get fees, placement reviews, exams required, cutoff & eligibility for all courses. B.Sc. (Hons.) in Food and Nutrition (3 years) Degree by West Bengal State University No. of Seats Exams 25 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ B.Com. (Hons.) in Accountancy (3 years) Degree by West Bengal State University Disclaimer: This PDF is auto-generated based on the information available on Shiksha as on 28-Sep-2021. No. of Seats Exams 79 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ B.Sc. (Hons.) in Geography (3 years) Degree by West Bengal State University No. of Seats Exams 58 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ B.A. (Hons.) in English (3 years) Disclaimer: This PDF is auto-generated based on the information available on Shiksha as on 28-Sep-2021. Degree by West Bengal State University No. of Seats Exams 62 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ B.A. (Hons.) in Political Science (3 years) Degree by West Bengal State University No. of Seats Exams 56 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ Disclaimer: This PDF is auto-generated based on the information available on Shiksha as on 28-Sep-2021. B.Sc. (Hons.) in Computer Science (3 years) Degree by West Bengal State University No. of Seats Exams 40 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ Bachelor of Commerce (B.Com.) (3 years) Degree by West Bengal State University No. of Seats Exams 100 ─ Total Fees Median Salary ─ ─ Course Rating Ranked ─ ─ Disclaimer: This PDF is auto-generated based on the information available on Shiksha as on 28-Sep-2021. -
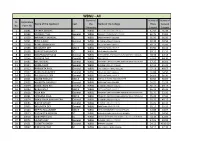
WBSU - All Name of Marks of Marks of SI
WBSU - All Name of Marks of Marks of SI. Application Name of the Applicant Cast the Name of the College Hons General No. Form No University Subject Subject 1 10281 JHARNA BISWAS SC WBSU EAST CALCUTTA GIRLS COLLEGE 61.50 56.33 2 10155 SATABDI PAUL General WBSU BARASAT GOVERNMENT COLLEGE 60.75 49.83 3 10159 MRINMOY MONDAL SC WBSU SREE CHAITANYA COLLEGE 60.50 66.50 4 10241 RITULA PAUL General WBSU BHAIRAB GANGULY COLLEGE 60.38 50.50 5 10158 RAMA SHANKHARI SC WBSU SREE CHAITANYA COLLEGE 60.13 55.66 6 10156 MOUMITA DEY OBC B WBSU SREE CHAITANYA COLLEGE 59.50 63.16 7 10238 SUROJIT MAJUMDER SC WBSU VIVEKANANDA COLLEGE 59.12 51.16 8 10060 SWAPNAMOY SAHA General WBSU BARRACKPORE RASTRAGURU SURENDRANATH COLLEGE 58.38 44.18 9 10166 SUDIPTA DAS General WBSU APC COLLEGE 57.63 44.33 10 10164 MILI BISWAS General WBSU PRASANTA CHANDRA MAHALANABISH MAHA VIDYALAYA 57.25 46.66 11 10114 SOMA DHAR General WBSU BHAIRAB GANGULY COLLEGE 57.13 51.33 12 10122 PARAMITA PAUL General WBSU EAST CALCUTTA GIRLS' COLLEGE 57.13 49.67 13 10152 RUMA MAJUMDER General WBSU SREE CHAITANYA COLLEGE 56.88 54.50 14 10154 PALLABI GOLDER General WBSU SREE CHAITANYA COLLEGE 56.63 56.30 15 10001 WAKIB HOSSAIN OBC A WBSU MRINALINI DATTA MAHAVIDYAPITH 56.50 48.67 16 10052 ANINDITA GANGULY General WBSU SREE CHINTANYA COLLEGE 56.25 51.33 17 10239 KAKALI BANERJEE General WBSU BHAIRAB GANGULY COLLEGE 56.13 49.17 18 10153 BABUL BALA OBC B WBSU SREE CHAITANYA COLLEGE 56.13 45.33 19 10028 PUJA ROY General WBSU PRASANTA CHANDRA MAHALANOBISH MAHAVIDYALAYA 55.75 52.00 20 10091 UPASANA PAUL OBC -

Education General Sc St Obc(A) Obc(B) Ph/Vh Total Vacancy 37 44 19 16 17 4 137 General
EDUCATION GENERAL SC ST OBC(A) OBC(B) PH/VH TOTAL VACANCY 37 44 19 16 17 4 137 GENERAL Sl No. University College Total 1 RAJ NAGAR MAHAVIDYALAYA 1 BURDWAN UNIVERSITY 2 SWAMI DHANANJAY DAS KATHIABABA MV, BHARA 1 3 AZAD HIND FOUZ SMRITI MAHAVIDYALAYA 1 4 BARUIPUR COLLEGE 1 5 DHOLA MAHAVIDYALAYA 1 6 HERAMBA CHANDRA COLLEGE 1 7 CALCUTTA UNIVERSITY MAHARAJA SRIS CHANDRA COLLEGE 1 8 SERAMPORE GIRLS' COLLEGE 1 9 SIBANI MANDAL MAHAVIDYALAYA 1 10 SONARPUR MAHAVIDYALAYA 1 11 SUNDARBAN HAZI DESARAT COLLEGE 1 12 GANGARAMPUR COLLEGE 1 13 GOURBANGA UNIVERSITY NATHANIEL MURMU COLLEGE 1 14 SOUTH MALDA COLLEGE 1 15 DUKHULAL NIBARAN CHANDRA COLLEGE 1 16 HAZI A. K. KHAN COLLEGE 1 17 KALYANI UNIVERSITY NUR MOHAMMAD SMRITI MAHAVIDYALAYA 1 18 PLASSEY COLLEGE 1 19 SUBHAS CHADRA BOSE CENTENARY COLLEGE 1 20 CLUNY WOMENS COLLEGE 1 21 LILABATI MAHAVIDYALAYA 1 NORTH BENGAL UNIVERSITY 22 NAKSHALBARI COLLEGE 1 23 RAJGANJ MAHAVIDYALAYA, RAJGANJ 1 24 ARSHA COLLEGE 1 SIDHO KANHO BIRSA UNIVERSITY 25 KOTSHILA MAHAVIDYALAYA 1 26 BHATTER COLLEGE 1 27 GOURAV GUIN MEMORIAL COLLEGE 1 28 PANSKURA BANAMALI COLLEGE 1 VIDYASAGAR UNIVERSITY 29 RABINDRA BHARATI MAHAVIDYALAYA 1 30 SIDDHINATH MAHAVIDYALAYA 1 31 SUKUMAR SENGUPTA MAHAVIDYALAYA 1 32 BARRAKPORE RASHTRAGURU SURENDRANATH COLLEGE 1 33 KALINAGAR MV 1 34 MAHADEVANANDA MAHAVIDYALAYA 1 WEST BENGAL STATE UNIVERSITY 35 NETAJI SATABARSHIKI MAHABIDYALAYA 1 36 P.N.DAS COLLEGE 1 37 RISHI BANKIM CHANDRA COLLEGE FOR WOMEN 1 OBC(A) 1 HOOGHLY WOMEN'S COLLEGE 1 BURDWAN UNIVERSITY 2 KABI JOYDEB MAHAVIDYALAYA 1 3 GANGADHARPUR MAHAVIDYALAYA -

Curriculum Vitae
CURRICULUM VITAE Name Dr. Jayanta Sen Designation Associate Professor of Economics Department Name Department of Economics University Telephone nos. : 033-25241975, Office Phone No 033-25241976, 033-25241978, 033-25241979 Email ID [email protected] , [email protected] Fax University Office Fax : (033) 2524 1977 Mobile No +91-8170908366 Institutional Website http://www.wbsubregistration.org/ West Bengal State University, Address Barasat, Kolkata-700126, West Bengal, India EDUCATIONAL QUALIFICATIONS 2006 Ph. D. (Economics), University of Kalyani, West Bengal, India. 1998 M. A. (Economics), University of Burdwan, West Bengal, India. Other Qualifications 1999 National Educational Test (NET), UGC. 1999 State Level Eligibility Test (SLET), WBCSC. CAREER PROFILE / TEACHING EXPERIENCE Associate Professor, Department of Economics, West Bengal State University, (Since May 13, 2017 Assistant) Professor, Department of Economics, West Bengal State University, (Since February 4, Assistant2009) Professor, V. S. Mahavidyalaya, West Medinipur, West Bengal. (Since May 13, 2005) Assistant Professor/Lecturer in Economics, The WB National University of Juridical Sciences, Salt Lake, Kolkata (Since January 3, 2005). Guest Faculty, Department of Economics, Sidho-Kanho-Birsha University, Purulia, West Bengal (2013-15) Guest Faculty, Department of Economics, Rabindra Bharati University, Kolkata (since 2016 & Continue) RESEARCH FELLOWSHIP Research Fellow, Dept. of Economics, University of Kalyani, under West Bengal State Govt. Scholarship Scheme (From 1999-2004) SPECIALIZATION/ TEACHING / RESEARCH AREAS Specialization Econometrics & Statistics Teaching Area Development Economics, Econometrics, Macroeconomics, Applied Econometrics Research Areas Income Inequality, Distribution and Wellbeing, Relative Deprivation, Poverty, Labour Economics, Issues on Development Economics SELECTED PUBLICATIONS IN JOURNALS/ EDITED BOOKS Journals 1. “Consumer Expenditure Inequality in India: A Source Decomposition Analysis”, International Journal of Development Issues, Vol. -

West Bengal State University, Barasat, 24 PGS (N) Schedule and Seat Allotment for B.Sc
West Bengal State University, Barasat, 24 PGS (N) Schedule and Seat allotment for B.Sc. Part I Practical Examinations, Zoology (Honours) – 2018 Reporting time: 10.45 Examination Centre Paper Date of Candidates allotted (122) Examination BKC College, 111/2 B.T.Road, Paper III 16.07.2018 Barrackpore Rastraguru Surendranath College Batch I (20) Bonhooghly, P.O. – Bonhooghly, (Monday) Kolkata 11 am ROLL NO. REGN. NO. 118212322149 1031721100491 118212322150 1031721400463 118212322151 1031721400490 118212322152 1031721100465 118212322153 1031721400464 118212322154 1031721100498 118212322155 1031721400470 118212322156 1031721100488 118212322157 1031721400508 118212322158 1031721400489 118212322159 1031721400466 118212322160 1031721400492 118212322161 1031721400478 118212322162 1031721400476 118212322163 1031721400497 Page 1 of 34 118212322164 1031721400456 118212322165 1031721100504 118212322166 1031721100474 118212322167 1031721300047 118212322168 1031721200473 BKC College, 111/2 B.T.Road, Paper III 17.07.2018 Barrackpore Rastraguru Surendranath College Batch II (20) Bonhooghly, P.O. – Bonhooghly, (Tuesday) Kolkata 11 am ROLL NO. REGN. NO. 118212322169 1031721400496 118212322170 1031721400505 118212322171 1031721400486 118212322172 1031721400462 118212322173 1031721100499 118212322174 1031721400469 118212322175 1031721400461 118212322176 1031721400460 118212322177 1031721300494 118212322178 1031721400482 118212322179 1031722400506 118212322180 1031721400468 118212322181 1031722300500 118212322182 1031721400495 118212322183 1031721300467 Page -
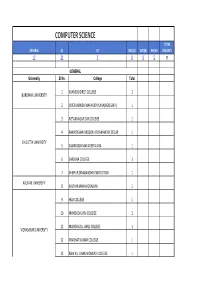
Computer Science Total General Sc St Obc(A) Obc(B) Ph/Vh Vacancy 17 31 7 9 9 0 73
COMPUTER SCIENCE TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 17 31 7 9 9 0 73 GENERAL University Sl No. College Total 1 ASANSOL GIRLS' COLLEGE 1 BURDWAN UNIVERSITY 2 VIVEKANANDA MAHAVIDYALAYA(HOOGHLY) 1 3 NETAJINAGAR DAY COLLEGE 1 4 RAMKRISHAN MISSION VIDYAMANDIR, BELUR 1 CALCUTTA UNIVERSITY 5 SAMMILANI MAHAVIDYALAYA 1 6 SARSUNA COLLEGE 1 7 SHIBPUR DINABANDHU INSTITUTION 1 KALYANI UNIVERSITY 8 KALYANI MAHAVIDYALAYA 1 9 HIJLI COLLEGE 1 10 MAHISADAL RAJ COLLEGE 1 11 MAHISHADAL GIRLS COLLEGE 1 VIDYASAGAR UNIVERSITY 12 PRABHAT KUMAR COLLEGE 1 13 RAJA N.L. KHAN WOMEN'S COLLEGE 1 14 VIVEKANANDA MISSION MAHAVIDYALAYA 1 15 BARASAT COLLEGE 1 WEST BENGAL STATE UNIVERSITY 16 DUM DUM MOTIJHEEL COLLEGE 1 17 MRINALINI DATTA MAHAVIDYAPITH 1 OBC(A) 1 RAJA RAMMOHAN ROY MAHAVIDYALAYA 1 BURDWAN UNIVERSITY 2 SRI RAMKRISHNA SARADA VIDYAMAHAPITHA 1 3 DHRUBA CHAND HALDER COLLEGE 1 CALCUTTA UNIVERSITY 4 JOGESH CHARDRA CHOUDHURI COLLEGE 1 5 RAMKRISHNA MISSION RESIDENTIAL COLLEGE 1 GOURBANGA UNIVERSITY 6 GOUR MAHAVIDYALAYA 1 7 CHANDRAKONA VIDYASAGAR MV 1 VIDYASAGAR UNIVERSITY 8 PANSKURA BANAMALI COLLEGE 1 9 VIVEKANANDA MISSION MAHAVIDYALAYA 1 OBC(B) 1 BANGABASI COLLEGE (DAY) 1 2 MAHESHTALA COLLEGE 1 CALCUTTA UNIVERSITY 3 NEW ALIPORE COLLEGE 1 4 NEW ALIPORE COLLEGE 1 NORTH BENGAL UNIVERSITY 5 SUKANTA MAHAVIDYALAYA 1 SIDHO KANHO BIRSA UNIVERSITY 6 PANCHAKOT MAHAVIDYALAYA 1 VIDYASAGAR UNIVERSITY 7 YOGODA SATSANGA PALPARA MAHAVIDYALAYA 1 8 BARRAKPORE RASHTRAGURU SURENDRANATH COLLEGE 1 WEST BENGAL STATE UNIVERSITY 9 PANIHATI MAHAVIDYALAYA 1 SC 1 ASANSOL GIRLS' COLLEGE 1 BURDWAN UNIVERSITY 2 MANKAR COLLEGE 1 3 MICHAEL MADHUSUDAN MEMORIAL COLLEGE 1 4 ANANDA MOHAN COLLEGE 1 5 ASUTOSH COLLEGE 1 6 ASUTOSH COLLEGE 1 7 BIDHAN CHANDRA COLLEGE(RISHRA) 1 CALCUTTA UNIVERSITY 8 CHARUCHANDRA COLLEGE 1 9 JOGESH CHARDRA CHOUDHURI COLLEGE 1 10 MAHESHTALA COLLEGE 1 11 RAMKRISHAN MISSION VIDYAMANDIR, BELUR 1 12 SHYAMPUR SIDDHESWARI MAHVIDYALAYA 1 GOURBANGA UNIVERSITY 13 GOUR MAHAVIDYALAYA 1 KALYANI UNIVERSITY 14 SRIKRISHNA COLLEGE 1 15 A.C. -

West Bengal State University
West Bengal State University Dist.: NORTH 24 PARGANAS Sl. No. Name of the College & Address Phone No. Email-id Acharya Prafulla Chandra Telefax: 2537 College[1960] 3297/8797 [email protected] 1. P.O. New Barrackpore, North 24 Phone: 2537 3297 Parganas, Kolkata 700 131 Amdanga Jugal Kishore Mahavidyalaya [2007] [email protected] 03216 260881 2. P.O. Sadhanpur-Uludanga, Amdanga om Pin 743 221 Bamanpukur Humayun Kabir 3. Mahavidyalaya [2006] 03217 260816 [email protected] Minakhan, P.O. Bamanpukur -743 425 Banipur Mahila Mahavidyalaya [1999] banipurmahilamahavidya 4. 03216 238243 P.O. Banipur- 743 233 [email protected] Barasat Govt. College [1950] 2552 3365 5. 10 KNC Road, Barasat [email protected] Fax : 25625053 Kolkata 700 124 barasatcollege72@yahoo. Barasat College [1972] 6. 2542 3656 co.in 1 Kalyani Road, P.O. Nabapally Fax: 2542 0454 principal@barasatcollege Barasat, Kolkata 700 126 .co.in Barrackpore Rashtraguru Surendranath College [1953] 2592 0603/8855 [email protected] 7. 85 Middle Road & Fax: 2594 5270 [email protected] 6 Riverside Road, Barrackpore Kolkata 700 120 [email protected] 8. Basirhat College [1947] 03217-228505 principalbcollege150@g P.O. Basirhat -743 412 mail.com Bhairab Ganguly College [1968] 9. 2553 2280 2 Feeder Road, Belghoria [email protected] 2564 3191 Kolkata 700 056 admin@bidhannagarcolle 10. Bidhannagar Govt. College [1984] 2337 4761 ge.org Bidhannagar, Kolkata 700 064 Fax: 23374382 bidhannagarcollege@vsnl .net Brahmananda Keshab Chandra College 11. [1956] 2577 2486 [email protected] 111/2, Barrackpore Trunk Road 2577 5878 m Bon-Hooghly, Kolkata 700 108 Sl. No. Name of the College & Address Phone No. -

Chandan Barman Assistant Professor & Head Department of Philosophy
Assistant Professor & Head PROFILE Chandan Barman Assistant Professor & Head Department of Philosophy Khatra Adibasi Mahavidyalaya, Khatra, Bankura, Pin-722140 Date of Birth: 01/06/1987 Date of Joining:04/10/2016 E. Mail Id- [email protected] Contact no – 9647844205 Academic Qualification B. Ed(S.E.D.E) from Netaji Subhash Open University in the year 2013 M. A( Philosophy) : from North Bengal University in the year 2010. B.A(Philosophy Honours) : from North Bengal University in the year 2008 Seminar /Confarence attained SL Nature of Organizing Institution Date no seminar /Confarence 1 One day National VIDYASAGAR UNIVERSITY PHILOSOPHY 25 JULY, 2021 Webinar ALUMNI ASSOCIATION 2 International Department of Buddhist Philosophy, June 27 & 28, 2020 Webinar Dharma Chakra Vihar International Institute of Origin Buddhist Studies and Research, Sarnath, Varanasi. 3 state level Nabadwip Vidyasagar College 27th June 2020 webinar Nabadwip, Nadia, West Bengal 4 Short term The department of philosophy, S. K. B. 26.8.2020 to 01.9.2020 Course U 5 state level PANIHATI MAHAVIDYALAYA 4th October 2020 webinar Barasat Road, Sodepur, Kolkata- 700110,West Bengal 6 National PATRASAYER MAHAVIDYALAYA 25th July, 2020 Webinar (AFFILIATED TO BANKURA UNIVERSITY) 7 National Khatra Adibasi Mahavidyalaya 22nd & 23rd July 2020 Webinar 8 National Bolpur college 03rd June to 5th June Webinar 2020 9 Faculty Induction Aligarh Muslim University (H. R. D. C) 23rd September to 31st Program october 2020 10 International Siddhinath Mahavidyalaya, West 16th july to 22nd -
Economics Total General Sc St Obc(A) Obc(B) Ph/Vh Vacancy 22 79 32 11 12 2 158
ECONOMICS TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 22 79 32 11 12 2 158 GENERAL University Sl No. College Total 1 DESHBANDHU MAHAVIDYALAYA 1 2 DURGAPUR WOMEN'S COLLEGE 1 3 KANDRA RADHA KANTO KUNDU MAHAVIDYALAYA 1 BURDWAN UNIVERSITY 4 PANCHMURA MAHAVIDYALAYA 1 5 SALDIHA COLLEGE 1 6 SAMBHUNATH COLLEGE 1 7 T.D.B. COLLEGE 1 8 ASUTOSH COLLEGE 1 9 K.K.DAS COLLEGE 1 10 NARASINHA DUTT COLLEGE 1 CALCUTTA UNIVERSITY 11 PRABHU JAGATBANDHU COLLEGE 1 12 SETH ANANDARAM JAIPURIA COLLEGE 1 13 SUNDARBAN HAZI DESARAT COLLEGE 1 GOURBANGA UNIVERSITY 14 BALURGHAT COLLEGE 1 15 BERHAMPUR COLLEGE 1 KALYANI UNIVERSITY 16 KANCHRAPARA COLLEGE 1 17 SUDHIRRANJAN LAHIRI MAHAVIDYALAYA 1 18 BHATTER COLLEGE 1 VIDYASAGAR UNIVERSITY 19 MIDNAPUR COLLEGE 1 20 BHAIRAB GANGULY COLLEGE 1 WEST BENGAL STATE UNIVERSITY 21 GOBARDANGA HINDU COLLEGE 1 22 NAHATA JOGENDRANATH MONDAL SMRITI MAHAVIDYALAYA 1 OBC(A) 1 BANKURA SAMMILANI COLLEGE 1 BURDWAN UNIVERSITY 2 DESHBANDHU MAHAVIDYALAYA 1 3 RABINDRA MV 1 4 CITY COLLEGE 1 5 CITY COLLEGE OF COMMERCE & BUSINESS ADMINISTRATION 1 CALCUTTA UNIVERSITY 6 HERAMBA CHANDRA COLLEGE 1 7 RAMSADAY COLLEGE 1 KALYANI UNIVERSITY 8 RANI DHANYA KUMARI COLLEGE 1 SIDHO KANHO BIRSA UNIVERSITY 9 NISTARINI COLLEGE 1 10 BASIRHAT COLLEGE 1 WEST BENGAL STATE UNIVERSITY 11 HIRALAL MAZUMDAR MEMORIAL COLLEGE FOR WOMEN 1 OBC(B) BURDWAN UNIVERSITY 1 KATWA COLLEGE 1 2 ANANDA MOHAN COLLEGE 1 3 CALCUTTA GIRLS' COLLEGE 1 CALCUTTA UNIVERSITY 4 JOGMAYA DEVI COLLEGE 1 5 MAHESHTALA COLLEGE 1 6 BALURGHAT COLLEGE 1 GOURBANGA UNIVERSITY 7 RAIGANJ SURENDRANATH MAHAVIDYALAYA -
Kaustav Chakraborty, Ph.D.(CU), Post-Doc(IICB)
Curriculum-Vitae Kaustav Chakraborty, Ph.D.(CU), Post-Doc(IICB) Corresponding Address: 53C/3, Dr. Suresh Chandra Banerjee Road, Beleghata, Kolkata-700010; West Bengal, India Phone No: +91-9836856131/6290392755 E-mail address: [email protected]; [email protected] Present Position: Assistant Professor (W.B.E.S), D/o Zoology, S.B.S. Government College, Hili, Dakshin Dinajpur, West Bengal Academics: . 2018 - 2019: DBT Research Associate (Post Doctorate) at Indian Institute of Chemical Biology, Kolkata. 2018: Doctor of Philosophy (PhD) in Science, Department of Zoology, University of Calcutta, Kolkata. 2011: M.Sc. in Zoology (Specialization – Immunology and Parasitology) from Maulana Azad College, University of Calcutta, Kolkata with 71.50% marks (1st class). 2009: B.Sc. (H) in Zoology from Maulana Azad College, University of Calcutta, Kolkata with 66% marks (1st class). 2006: 12th from Hare School, West Bengal Council of Higher Secondary Education with 79.5% marks (1st division). 2004: 10th from Hare School, West Bengal Board of Secondary Education with 82.6% marks (1st division). Teaching Experience: 30th September, 2019 – Present: Assistant Professor (W.B.E.S), D/o Zoology, S.B.S. Govt. College, Hili, West Bengal 1st February, 2019 – 28th September, 2019: Guest Lecturer, D/o Zoology, Ramakrishna Mission Vidyamandira, Belur Math, Howrah, West Bengal 1st September, 2017 – 31st August, 2018: Guest Lecturer, D/o Zoology, Basirhat College, Basirhat, West Bengal Professional & Other Experience: . Co-Convener & Host of the Organizing Committee for One Day National Webinar entitled “Fight Against COVID-19: We Shall Overcome” jointly organized by D/o Zoology, Botany & Chemistry in collaboration with IQAC, S.B.S. -

West Bengal State University
West Bengal State University District: NORTH 24 PARGANAS Sl. No. Name of the College & Address Phone No. Email-id Acharya Prafulla Chandra 1. College[1960] Fax: 2537 3297/8797 [email protected] P.O. New Barrackpore, North 24 Phone: 2537 3297 Parganas, Kolkata 700 131 Amdanga Jugal Kishore 2. Mahavidyalaya [2007] 03216 260881 P.O. Sadhanpur-Uludanga, Amdanga-743 221 Bamanpukur Humayun Kabir 3. Mahavidyalaya [2006] 03217 260816 Minakhan, P.O. Bamanpukur -743 425 Banipur Mahila Mahavidyalaya 4. [1999] 03216 238243 [email protected] P.O. Banipur- 743 233 Barasat Govt. College [1950] 5. 10 KNC Road,Barasat 2552 3365 [email protected] Kolkata 700 124 Fax : 25625053 Barasat College [1972] [email protected] 6. 1 Kalyani Road, P.O. Nabapally 2542 3656 [email protected] Barasat, Kolkata 700 126 Fax: 2542 0454 Barrackpore Rashtraguru Surendranath College [1953] 7. [email protected] 85 Middle Road & 2592 0603/8855 [email protected] 6 Riverside Road, Barrackpore Fax: 2594 5270 Kolkata 700 120 8. Basirhat College [1947] 03217-228505 P.O. Basirhat -743 412 Bhairab Ganguly College [1968] 9. 2553 2280 2 Feeder Road,Belghoria Kolkata [email protected] 2564 3191 700056 Bidhannagar Govt. College [1984] [email protected] 10. Bidhannagar, Kolkata 700 064 2337 4761 [email protected] Fax: 23374382 Brahmananda Keshab Chandra College [1956] 2577 2486 11. 111/2, Barrackpore Trunk Road 2577 5878 [email protected] Bon-Hooghly, Kolkata 700 108 Brainware College of Professional Studies Barasat 033 – 6499- 12. 398, Ramkrishnapur Road, 1284/9748403098 Barasat (Near Jagadighata Market) Kolkata-700124 Chandraketugarh Sahidullah 13. Smriti Mahavidyalaya [1997] P.O. -

THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-Aided Colleges of West Bengal (Advt
THE WEST BENGAL COLLEGE SERVICE COMMISSION Vacancy Status (Tentative) for the Posts of Assistant Professor in Government-aided Colleges of West Bengal (Advt. No. 1/2018) ZOOLOGY UR OBC-A OBC-B SC ST PWD 37 15 6 18 22 7 Sl No College University UR 1 Burdwan Raj College 2 Katwa College (Day+ Evening) 3 Netaji Mahavidyalaya BURDWAN UNIVERSITY 4 Raja Ram Mohon Roy Mahavidyalaya 5 Rampurhat College 6 Bangabasi Morning College 7 City College 8 Dhruba Chand Halder College 9 Netaji Nagar College for Women CALCUTTA UNIVERSITY 10 Raja Peary Mohan College 11 Sundarban Hazi Desarat College 12 Vidyanagar College 13 Kaliachak College GOUR BANGA UNIVERSITY 14 Chakdaha College 15 Dukhulal Nibaran Chandra College KALYANI UNIVERSITY 16 Dukhulal Nibaran Chandra College 17 Jangipur College 18 Banwarilal Bhalotia College, Asansol 19 Banwarilal Bhalotia College, Asansol KAZI NAZRUL UNIVERSITY 20 Banwarilal Bhalotia College, Asansol (ASANSOL) 21 Banwarilal Bhalotia College, Asansol 22 Raniganj Girls' College 23 Ananda Chandra College NORTH BENGAL UNIVERSITY 24 Parimal mitra smriti mahavidyalaya 25 Balarampur College SIDHO KANHO BIRSHA UNIVERSITY 26 Jagannath Kishore College 27 Belda College 28 Ghatal Rabindra Satabarsiki Mahavidyalaya VIDYASAGAR UNIVERSITY 29 Midnapore College 30 Narajole Raj College 31 Acharya Prafulla Chandra College 32 Bhairab Ganguly College 33 Brahmananda Keshab Chandra College 34 Brahmananda Keshab Chandra College WEST BENGAL STATE UNIVERSITY 35 East Calcutta Girls' College, Lake Town 36 Sarojini Naidu College for Women 37 Sarojini Naidu