DOCSLIB.ORG

GEO-SCI 587 HYDROGEOLOGY Problem Set #1 Answers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
GEO-SCI 587 HYDROGEOLOGY Problem Set #1 Answers GEO-SCI 587 HYDROGEOLOGY Problem Set #1 Answers 1) Total Points: 10 Darcy’s Law (in a porous medium under linear conditions) relates the flow rate of water to the physical properties of the system, including area of flow, head, length of flow, and characteristics of the medium through which the flow is occurring. Q = - K A dh/dl The flow rate is directly proportional to the hydraulic conductivity of the medium, the cross-sectional area of flow, and head loss. It is inversely proportional to the length of flow. 2) Total Points: 20 Given: dL = 60 cm D = 10 cm R = D / 2 = 10 / 2 = 5 cm A = π * R2 = π * 25 = 78.5 cm2 K = 600 cm/d n = 0.20 hptop = 30 cm hpbottom = 80 cm Solution: Use the bottom end of the column as the datum. > Find the direction of flow httop = hptop + hztop = 30 cm + 60 cm = 90 cm htbottom = hpbottom + hzbottom = 80 cm + 0 cm = 80 cm Flow will be from high to low total head, or downward. hp = 30 cm hz = 60 cm ht = 30 + 60 = 90 cm dL = 60 cm hp = 80 cm hz = 0 cm ht = 80 + 0 = 80 cm > Calculate Q, q, and v Q = - K * A * dh/dL = - (600 cm/d) * (78.5 cm2) * (80 – 90 cm) / 60 cm Q = 7850 cm3/d Convert to cm3/min… 7850 cm3/d * (1 d / 1440 min) = 5.45 cm3/min q = Q / A = [5.45 cm3/min] / [78.5 cm2] = 0.069 cm/min v = q / n = [0.069 cm / min] / [0.20] = 0.35 cm/min > Is “Darcy velocity” (q) or “Average Linear Pore Water Velocity” (v) always larger in a porous medium? In the case where n<1 (a porous medium)… v > q since v = q / n (garden hose analogy) 3) Total Points: 15 a. Basin as a whole Inputs Outputs Precip 35 in/yr Evaporation 23 in/yr Streamflow (Total) 9 in/yr Subsea Outflow 3 in/yr b. Streams Inputs Outputs Stormflow 3 in/yr Streamflow (Total) 9 in/yr Baseflow 6 in/yr c. groundwater Inputs Outputs Recharge 9 in/yr Baseflow 6 in/yr Subsea Outflow 3 in/yr d. Average streamflow from the basin in cfs ~130 ft3/s A= 200 mi2 = 5.6 E9 ft2 Streamflow is calculated by taking length per time unit and multiplying by catchment area. e. Groundwater recharge First convert the 9 in/yr into ft3/day by using same technique used above, next convert to gallons per day, then divide answer by 200 mi2 to give you 419,000 gallons of water per sq. mile of surface area. Now divide by 1e6 to give you .419 millions of gallons water per day per sq. mile of surface area. 4) Total Points: 20 Given: A B C Depth to water (m) 15 40 40 Depth of Piezometer 140 70 100 (m) Use the bedrock surface as the datum for elevation head. A B C depth elevation above the datum 0m hz = 150 m water level 50 m 100 m shale 150 m hz = 0m > Part a: Calculate pressure, elevation, and hydraulic head hp = depth of piezometer – depth to water This is like the depth of water over your point of measurement. hz = depth to bedrock – depth of piezometer This is the elevation of your point of measure above some datum. ht = hp + hz A B C Pressure head (m) 140-15= 125 70-40= 30 100-40= 60 Elevation head (m) 150-140= 10 150-70= 80 150-100= 50 Hydraulic head (m) 125+10= 135 80+30= 110 60+50= 110 > Part b: Calculate the average vertical gradients. What is the significance of the results? A Æ B : dh/dl = [110-135] / [140-70] = - 0.36 There is a gradient from A to B. However, since there is a confining layer between them, there will not be significant flow, unless the aquitard is leaky. If there is water transmitted, it will be from A to B. B Æ C : dh / dl = [110-110] / [100-70] = 0 There is no gradient in total head, so there will be no flow between B and C. > Part c: Did the company do unnecessary work? YES. Wells B and C are in the same, unconfined aquifer. (Well A is in a different aquifer that is confined.) > Part d: To minimize pumping costs, you would want to pump from well A. Here, the water is only 15 vertical meters from the surface, versus 40 meters in the case of wells B and C. 5) Total Points: 20 First, calculate the total head at each of the three points. Total head at each point will be equal to [(land surface elevation)-(depth to water)-(elevation of datum)]. If we choose sea level as our datum, total head is simply [(land surface elevation)-(depth to water)]. Point 1: 5438 m – 49 m = 5389 m Point 2: 5442 m – 52 m = 5390 m Point 3: 5446 m – 55 m = 5391 m Next, plot the points on graph paper and label the head at each point (Figure). Since we only have three points available to define our potentiometric surface, we must assume it is planar. If the surface is planar, the gradient in any direction will be linear. As a result, we can interpret head values between holes 1, 2, and 3 along the lines connecting them. For instance, because the total head at point 1 is 5389 m and total head at point 3 is 5391 m, we can assume that the head half way between the two points is 5390 m. Now, draw lines connecting points of equal head to create equipotential lines (we only have two sets of points with equal head values, but all the equipotentials are parallel and equally spaced, so we can draw in other lines based on points where one head value is known). Assuming a homogenous, isotropic medium, groundwater flow will be perpendicular to the equipotentials, from high total head to low total head. In the scenario presented, flow is to the southwest (260 degrees). The distance (∆l) from the 5391 m equipotential to the 5389 m equipotential (∆h = 2 m) is 5 inches, so the hydraulic gradient is 2 m/(5 in * 200 m/in) = 2 m/1000 m = 2 x 10-3. 6) Total Points: 15 First, determine the total head at point A and D. Point A: 5 m Point D: 4 m We know that the total head is linear between these points, so Point B: 4.67 m Point C: 4.33 m Determine elevation head at all points. Point A: 5 m Point B: 0 m Point C: 0 m Point D: 4 m Next determine pressure head at A and D. Point A: 0 m Point D: 0 m Calculate pressure head at B and C using the equation: hT = hE + hP. Point B: 4.67 – 0 = 4.67 m Point C: 4.33 – 0 = 4.33 m Total, elevation and pressure head 5 4 ) ht m 3 ( he 2 ead hp h 1 0 012345678910111213 length (m) .
Load more

Recommended publications
  • Hydrogeology
    Hydrogeology Principles of Groundwater Flow Lecture 3 1 Hydrostatic pressure The total force acting at the bottom of the prism with area A is Dividing both sides by the area, A ,of the prism 1 2 Hydrostatic Pressure Top of the atmosphere Thus a positive suction corresponds to a negative gage pressure. The dimensions of pressure are F/L2, that is Newton per square meter or pascal (Pa), kiloNewton per square meter or kilopascal (kPa) in SI units Point A is in the saturated zone and the gage pressure is positive. Point B is in the unsaturated zone and the gage pressure is negative. This negative pressure is referred to as a suction or tension. 3 Hydraulic Head The law of hydrostatics states that pressure p can be expressed in terms of height of liquid h measured from the water table (assuming that groundwater is at rest or moving horizontally). This height is called the pressure head: For point A the quantity h is positive whereas it is negative for point B. h = Pf /ϒf = Pf /ρg If the medium is saturated, pore pressure, p, can be measured by the pressure head, h = pf /γf in a piezometer, a nonflowing well. The difference between the altitude of the well, H, and the depth to the water inside the well is the total head, h , at the well. i 2 4 Energy in Groundwater • Groundwater possess mechanical energy in the form of kinetic energy, gravitational potential energy and energy of fluid pressure. • Because the amount of energy vary from place-­­to-­­place, groundwater is forced to move from one region to another in order to neutralize the energy differences.
    [Show full text]
  • CPT-Geoenviron-Guide-2Nd-Edition
    Engineering Units Multiples Micro (P) = 10-6 Milli (m) = 10-3 Kilo (k) = 10+3 Mega (M) = 10+6 Imperial Units SI Units Length feet (ft) meter (m) Area square feet (ft2) square meter (m2) Force pounds (p) Newton (N) Pressure/Stress pounds/foot2 (psf) Pascal (Pa) = (N/m2) Multiple Units Length inches (in) millimeter (mm) Area square feet (ft2) square millimeter (mm2) Force ton (t) kilonewton (kN) Pressure/Stress pounds/inch2 (psi) kilonewton/meter2 kPa) tons/foot2 (tsf) meganewton/meter2 (MPa) Conversion Factors Force: 1 ton = 9.8 kN 1 kg = 9.8 N Pressure/Stress 1kg/cm2 = 100 kPa = 100 kN/m2 = 1 bar 1 tsf = 96 kPa (~100 kPa = 0.1 MPa) 1 t/m2 ~ 10 kPa 14.5 psi = 100 kPa 2.31 foot of water = 1 psi 1 meter of water = 10 kPa Derived Values from CPT Friction ratio: Rf = (fs/qt) x 100% Corrected cone resistance: qt = qc + u2(1-a) Net cone resistance: qn = qt – Vvo Excess pore pressure: 'u = u2 – u0 Pore pressure ratio: Bq = 'u / qn Normalized excess pore pressure: U = (ut – u0) / (ui – u0) where: ut is the pore pressure at time t in a dissipation test, and ui is the initial pore pressure at the start of the dissipation test Guide to Cone Penetration Testing for Geo-Environmental Engineering By P. K. Robertson and K.L. Cabal (Robertson) Gregg Drilling & Testing, Inc. 2nd Edition December 2008 Gregg Drilling & Testing, Inc. Corporate Headquarters 2726 Walnut Avenue Signal Hill, California 90755 Telephone: (562) 427-6899 Fax: (562) 427-3314 E-mail: [email protected] Website: www.greggdrilling.com The publisher and the author make no warranties or representations of any kind concerning the accuracy or suitability of the information contained in this guide for any purpose and cannot accept any legal responsibility for any errors or omissions that may have been made.
    [Show full text]
  • Table of Common Symbols Used in Hydrogeology
    Common Symbols used in GEOL 473/573 A Area [L2] b Saturated thickness of an aquifer [L] d Diameter [L] e void ratio (dimensionless) or e1 is a constant = 2.718281828... f Number of head drops in a flow of net F Force [M L T-2 ] g Acceleration due to gravity [9.81 m/s2] h Hydraulic head [L] (Total hydraulic head; h = ψ + z) ho Initial hydraulic head [L], generally an initial condition or a boundary condition dh/dL Hydraulic gradient [dimensionless] sometimes expressed as i 2 ki Intrinsic permeability [L ] K Hydraulic conductivity [L T-1] -1 Kx, Ky , Kz Hydraulic conductivity in the x, y, or z direction [L T ] L Length from one point to another [L] n Porosity [dimensionless] ne Effective porosity [dimensionless] q Specific discharge [L T-1] (Darcy flux or Darcy velocity) -1 qx, qy, qz Specific discharge in the x, y, or z direction [L T ] Q Flow rate [L3 T-1] (discharge) p Number of stream tubes in a flow of net P Pressure [M L-1T-2] r Radial coordinate [L] rw Radius of well over screened interval [L] Re Reynolds’ number [dimensionless] s Drawdown in an aquifer [L] S Storativity [dimensionless] (Coefficient of storage) -1 Ss Specific storage [L ] Sy Specific yield [dimensionless] t Time [T] T Transmissivity [L2 T-1] or Temperature (degrees) u Theis’ number [dimensionless} or used for fluid pressure (P) in engineering v Pore-water velocity [L T-1] (Average linear velocity) V Volume [L3] 3 VT Total volume of a soil core [L ] 3 Vv Volume voids in a soil core [L ] 3 Vw Volume of water in the voids of a soil core [L ] Vs Volume soilds in a soil
    [Show full text]
  • Darcy's Law and Hydraulic Head
    Darcy’s Law and Hydraulic Head 1. Hydraulic Head hh12− QK= A h L p1 h1 h2 h1 and h2 are hydraulic heads associated with hp2 points 1 and 2. Q The hydraulic head, or z1 total head, is a measure z2 of the potential of the datum water fluid at the measurement point. “Potential of a fluid at a specific point is the work required to transform a unit of mass of fluid from an arbitrarily chosen state to the state under consideration.” Three Types of Potentials A. Pressure potential work required to raise the water pressure 1 P 1 P m P W1 = VdP = dP = ∫0 ∫0 m m ρ w ρ w ρw : density of water assumed to be independent of pressure V: volume z = z P = P v = v Current state z = 0 P = 0 v = 0 Reference state B. Elevation potential work required to raise the elevation 1 Z W ==mgdz gz 2 m ∫0 C. Kinetic potential work required to raise the velocity (dz = vdt) 2 11ZZdv vv W ==madz m dz == vdv 3 m ∫∫∫00m dt 02 Total potential: Total [hydraulic] head: P v 2 Φ P v 2 h == ++z Φ= +gz + g ρ g 2g ρw 2 w Unit [L2T-1] Unit [L] 2 Total head or P v hydraulic head: h =++z ρw g 2g Kinetic term pressure elevation [L] head [L] Piezometer P1 P2 ρg ρg h1 h2 z1 z2 datum A fluid moves from where the total head is higher to where it is lower. For an ideal fluid (frictionless and incompressible), the total head would stay constant.
    [Show full text]
  • Comparative Performance Evaluation of Pelton Wheel and Cross Flow Turbines for Power Generation
    EUROPEAN MECHANICAL SCIENCE Research Paper e-ISSN: 2587-1110 Comparative Performance Evaluation of Pelton Wheel and Cross Flow Turbines for Power Generation Oyebode O. O.1* and Olaoye J. O.2 1Department of Food, Agricultural and Biological Engineering, Kwara State University, Malete, Kwara State, Nigeria. 2Department of Agricultural and Biosystems Engineering, University of Ilorin, Ilorin, Kwara State, Nigeria. ORCID: Oyebode (0000-0003-1094-1149) Abstract The performance of two micro hydro power turbines (Pelton Wheel and Cross Flow Turbines) were evaluated at the University of Ilorin (UNILORIN) dam. The Dam has a net head of 4 m, flow rate of 0.017m3 and theoretical hydropower energy of 668W. The two turbines were tested and the optimized value of operating conditions namely; angle of inclination (15o above tangent, tangential and 15o below tangent), height to impact point (200mm, 250mm and 300mm) and length to impact point (50mm, 100mm and 150mm) were pre-set at their various levels for both Turbines. The optimum values of the process output or measured parameters were determined statistically using a 33X2 factorial experiment in three replicates. An optimum Turbine speed (538.38rpm) in off load condition was achieved at 250mm height to impact point, 150mm length to impact point and angle at tangential inclination. Similar combination also yielded an optimum turbine torque of 46.16kNm for Pelton Wheel Turbine. For the Crossflow Turbine, an optimum turbine speed of 330.09rpm was achieved by pre-setting 250mm height to impact point, 100mm length to impact point and 15º below tangent. Same combination also yielded an optimum turbine torque of 39.07kNm.
    [Show full text]
  • Helical Turbine for Hydropower
    Tidewalker Engineering / Optimization of GHT Production Marine and Hydrokinetic Technology Readiness Advancement Initiative Funding Opportunity Announcement Number: DE-FOA-0000293 CFDA Number: 81.087 PROJECT NARRATIVE Tidewalker Engineering Trescott, Maine Title: Optimization of Gorlov Helical Turbine Production June 2010 Table of Contents: SUBJECT PAGE NUMBER Introduction: Project Narrative 2 Project Objectives 3 Merit Review Criteria Discussion 7 Project Timetable 13 Relevance and Outcomes / Impacts 14 Role of Participants 14 Facilities and Other Resources 15 Equipment 15 Bibliography and References 16 Appendix- A / Letter of Commitment 17 Appendix – B / Velocity Measurements 18 Appendix – C / GHT Applications 19 Appendix – D / Cost Sharing Grant 32 1 Tidewalker Engineering / Optimization of GHT Production Project Narrative: Under this proposal Tidewalker Engineering with the assistance of Dr. Alexander Gorlov and other specialists will investigate the feasibility of placing a hydro-kinetic device into a flexible dam system to generate electricity from tidal flows at sites with a substantial tidal range (average value of 18’). The study will also include the design of a turbo-generator unit which optimizes electrical production from this proposed mode of operation. Environmental issues associated with the placement of a flexible dam into a tidal flow will be analyzed in terms of regulatory licensing requirements. The applicability of this proposed mode of operation will be addressed as part of expected project benefits from the development potential of this concept. The eligibility standard as expressed in published responses within the Federal Connect network for this grant application directly addressed the issue of diversionary structures as excerpted below: DOE will not consider any application under this FOA for the development of a technology that would require blocking or severely altering existing tidal or river flows, as this would be considered a dam or diversionary structure.
    [Show full text]
  • Salt Flow Example
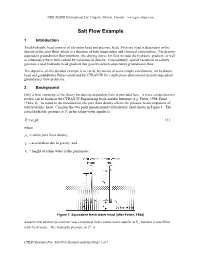
    GEO-SLOPE International Ltd, Calgary, Alberta, Canada www.geo-slope.com Salt Flow Example 1 Introduction Total hydraulic head consists of elevation head and pressure head. Pressure head is dependent on the density of the pore fluid, which is a function of both temperature and chemical composition. For density- dependent groundwater flow problems, the driving forces for flow include the hydraulic gradient, as well as a buoyancy force term caused by variations in density. Consequently, spatial variations in salinity generate a total hydraulic head gradient that governs density-dependent groundwater flow. The objective of this detailed example is to verify, by means of some simple calculations, the hydraulic head and groundwater fluxes calculated by CTRAN/W for coupled one-dimensional density-dependent groundwater flow problems. 2 Background Only a brief summary of the theory for density-dependent flow is provided here. A more comprehensive review can be found in the CTRAN/W Engineering book and the literature (e.g. Fetter, 1998; Frind, 1982a, b). As noted in the introduction, the pore fluid density affects the pressure head component of total hydraulic head. Consider the two point measurements of hydraulic head shown in Figure 1. The actual hydraulic pressure at P1 in the saline-water aquifer is P1 ss gh [1] where s = saline pore fluid density; g = acceleration due to gravity; and, hs = height of saline water in the piezometer. Figure 1 Equivalent fresh water head (after Fetter, 1988) Assume that another piezometer was completed in the saline-water aquifer at P2 , but that it was filled with fresh water.
    [Show full text]
  • The Cause and Statistical Analysis of the River Valley Contractions at the Xiluodu Hydropower Station, China
    water Article The Cause and Statistical Analysis of the River Valley Contractions at the Xiluodu Hydropower Station, China Mingwei Li 1 , Zhifang Zhou 1,*, Chao Zhuang 1 , Yawen Xin 1 , Meng Chen 2 and Jian Wu 1 1 School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, China; [email protected] (M.L.); [email protected] (C.Z.); [email protected] (Y.X.); [email protected] (J.W.) 2 College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China; [email protected] * Correspondence: [email protected] Received: 2 January 2020; Accepted: 8 March 2020; Published: 12 March 2020 Abstract: The Xiluodu Dam is a concrete double-curvature arch dam with a crest elevation of 610 m and a height of 285.5 m. Since the impoundment of the Xiluodu reservoir, remarkable river valley contractions (RVCs) have been observed upstream and downstream of the reservoir, potentially threatening the safety of the dam. However, the cause of these RVCs remains unclear. Based on an analysis of hydrogeological conditions, the RVCs were determined a result of the expansion of the aquifer, within which the effective stress decreased due to an increase in the hydraulic head after reservoir impoundment. Referring to the hydrostatic seasonal time (HST) model, a groundwater hydrostatic seasonal (GHS) model is proposed for simulating and predicting the development of the RVCs. Unlike the HST model, the GHS model can provide information on aquifer hydraulic diffusivity. The calibration results illustrate that the GHS model can accurately fit the observed RVCs data. The calculation results revealed that the RVCs were mainly affected by the hydraulic head of the confined aquifer, and that seasonal effects gave rise to less than 10% of the total RVCs.
    [Show full text]
  • Low Head Hydropower for Local Energy Solutions
    Low Head Hydropower for Local Energy Solutions A.G. Pradeep Narrain LOW HEAD HYDROPOWER FOR LOCAL ENERGY SOLUTIONS LOW HEAD HYDROPOWER FOR LOCAL ENERGY SOLUTIONS DISSERTATION Submitted in fulfillment of the requirements of the Board for Doctorates of Delft University of Technology and of the Academic Board of the UNESCO-IHE Institute for Water Education for the Degree of DOCTOR to be defended in public on Monday, 9 October 2017, at 10:00 hours in Delft, the Netherlands by Arcot Ganesh Pradeep NARRAIN Master of Science in Water Resources Engineering and Management University of Stuttgart, Germany born in Bangalore, India This dissertation has been approved by the promotors: Prof.dr.ir. A.E. Mynett Prof.dr. N.G. Wright Composition of the doctoral committee: Chairman Rector Magnificus Delft University of Technology Vice-Chairman Rector UNESCO-IHE Prof.dr.ir. A.E. Mynett UNESCO-IHE / Delft University of Technology, promotor Prof.dr. N.G. Wright De Montfort University, UK / UNESCO-IHE, promotor Independent members: Prof.dr.ir. W.S.J. Uijttewaal Delft University of Technology Prof.dr.ir. C. Zevenbergen UNESCO-IHE / Delft University of Technology Prof. dr. G. Pender Heriot-Watt University, UK Prof.dr.-ing. U. Gärtner Esslingen University of Applied Sciences, Germany Prof.dr.ir. H.H.G. Savenije Delft University of Technology, reserve member CRC Press/Balkema is an imprint of the Taylor & Francis Group, an informa business © 2017, A.G. Pradeep Narrain Although all care is taken to ensure integrity and the quality of this publication and the information herein, no responsibility is assumed by the publishers, the author nor UNESCO- IHE for any damage to the property or persons as a result of operation or use of this publication and/or the information contained herein.
    [Show full text]
  • Kinetic and Friction Head Loss Impacts on Horizontal
    KINETIC AND FRICTION HEAD LOSS IMPACTS ON HORIZONTAL WATER SUPPLY AND AQUIFER STORAGE AND RECOVERY WELLS A Thesis by BENJAMIN JOSEPH BLUMENTHAL Submitted to the Office of Graduate and Professional Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Chair of Committee, Hongbin Zhan Committee Members, Peter Knappett Sungyon Lee Head of Department, John R. Giardino December 2014 Major Subject: Geology Copyright 2014 Benjamin Joseph Blumenthal ABSTRACT Groundwater wells can have extreme pressure buildup when injecting and extreme pressure drawdown when extracting. Greater wellbore contact with the aquifer minimizes pressure buildup and pressure drawdown. Aquifers are usually much more laterally extensive than vertically thick. Therefore, horizontal wells can be longer than vertical wells thus increasing aquifer contact and minimizing pressure issues. The length and therefore the effectiveness of horizontal wells are limited by two factors, either well construction or intra-wellbore head loss. Currently no analytical groundwater model rigorously accounts for intra- wellbore kinetic and friction head loss. We have developed a semi-analytical, intra- wellbore head loss model dynamically linked to an aquifer. This model is the first of its kind in the groundwater literature. We also derived several new boundary condition solutions that are rapidly convergent at all times. These new aquifer solutions do not require approximation or pressure pulse tracking. We verified our intra-wellbore head loss model against MODFLOW-CFP and found matches of three significant figures. We then completed 360 simulations to investigate intra-wellbore head loss. We found that only when aquifer drawdown was small will intra-wellbore head loss be relatively important.
    [Show full text]
  • Stream Water Wheels As Renewable Energy Supply in flowing Water: Theoretical Considerations, Performance Assessment and Design Recommendations
    Energy for Sustainable Development 45 (2018) 96–109 Contents lists available at ScienceDirect Energy for Sustainable Development Review Stream water wheels as renewable energy supply in flowing water: Theoretical considerations, performance assessment and design recommendations Emanuele Quaranta Politecnico di Torino, DIATI (Department of Environment, Land and Infrastructure Engineering), Corso Duca degli Abruzzi 24, 10129 Torino, Italy ARTICLE INFO ABSTRACT Article history: Water wheels were the earliest hydraulic machines used in antiquity to convert water energy into mechan- Received 8 February 2018 ical one. Due to their simple installation, low maintenance costs, and thanks to the possibility to use local Received in revised form 7 May 2018 manpower and material for their construction, nowadays water wheels are again used as energy supply, Accepted 8 May 2018 especially in remote localities and emerging countries. In particular, stream water wheels are installed in Available online xxxx flowing water where there are not head differences. The performance depends on the blockage ratio, so that they can be subdivided into three main categories: stream wheels in shallow subcritical flow, shallow Keywords: supercritical flow and deep flow. Deep water In this paper, experimental, theoretical and numerical data on stream water wheels were systematically Floating wheels Micro-hydro collected from literature and analyzed. Guidelines for their design were discussed focusing especially on Shallow water wheel dimensions, supporting structures, blades and speed. More light on their hydraulic behavior was Stream water wheels shed, adopting the previous classification for a better explanation and understanding. Results showed that in shallow water an head difference can be generated by the wheel, increasing the power output.
    [Show full text]
  • A Techno-Economical View on Energy Losses at Hydropower Dams (Case Study of Karun III Dam and Hydropower Plant)
    Computational Methods in Multiphase Flow VI 253 A techno-economical view on energy losses at hydropower dams (case study of Karun III Dam and Hydropower Plant) M. Jorabloo1, M. Abdolahpour2, R. Roshan2 & H. Sarkardeh2 1Department of Engineering, Water Engineering Group, Islamic Azad University, Iran 2Hydraulic Structures Division, Water Research Institute, Iran Abstract In order to support the future economic developments in the world, one of the most important objectives is the reduction of energy losses. Apart from this objective, hydropower dams which are considered a renewable energy source encounter this problem. Karun III Dam and Hydropower Plant is constructed on the Karun River in the province of Khuzestan, Iran, with a capacity of 2000 MW. The Dam is a double arch concrete type, 205m high from the foundation and 185m high from the river bed. In the present work by using the physical model of Karun III Dam and measuring pressures in all parts of conveyance members, energy losses for each part were calculated separately. Experiments were conducted in three different elevations and with maximum design discharge. By calculating the cavitation index along the related hydraulic structures, probability of cavitation was studied. Discharge coefficient was also estimated in the operation conditions. Experiments showed that when the reservoir elevation was increased in constant discharge; the discharge coefficient was increased respectively. Also it was observed that increasing the reservoir elevation causes head losses to increase in different parts of conveyance members except the anti- vortex structure which was installed at the top of the intake. Moreover, energy losses at the Y-Branch member were observed more than other parts.
    [Show full text]