Orientational Correlations in Liquid Acetone and Dimethyl Sulfoxide: a Comparative Study Sylvia E
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dimethyl Sulfoxide MSDS
He a lt h 1 2 Fire 2 2 0 Re a c t iv it y 0 Pe rs o n a l Pro t e c t io n F Material Safety Data Sheet Dimethyl sulfoxide MSDS Section 1: Chemical Product and Company Identification Product Name: Dimethyl sulfoxide Contact Information: Catalog Codes: SLD3139, SLD1015 Sciencelab.com, Inc. 14025 Smith Rd. CAS#: 67-68-5 Houston, Texas 77396 RTECS: PV6210000 US Sales: 1-800-901-7247 International Sales: 1-281-441-4400 TSCA: TSCA 8(b) inventory: Dimethyl sulfoxide Order Online: ScienceLab.com CI#: Not applicable. CHEMTREC (24HR Emergency Telephone), call: Synonym: Methyl Sulfoxide; DMSO 1-800-424-9300 Chemical Name: Dimethyl Sulfoxide International CHEMTREC, call: 1-703-527-3887 Chemical Formula: (CH3)2SO For non-emergency assistance, call: 1-281-441-4400 Section 2: Composition and Information on Ingredients Composition: Name CAS # % by Weight Dimethyl sulfoxide 67-68-5 100 Toxicological Data on Ingredients: Dimethyl sulfoxide: ORAL (LD50): Acute: 14500 mg/kg [Rat]. 7920 mg/kg [Mouse]. DERMAL (LD50): Acute: 40000 mg/kg [Rat]. Section 3: Hazards Identification Potential Acute Health Effects: Slightly hazardous in case of inhalation (lung irritant). Slightly hazardous in case of skin contact (irritant, permeator), of eye contact (irritant), of ingestion, . Potential Chronic Health Effects: Slightly hazardous in case of skin contact (irritant, sensitizer, permeator), of ingestion. CARCINOGENIC EFFECTS: Not available. MUTAGENIC EFFECTS: Mutagenic for mammalian somatic cells. Mutagenic for bacteria and/or yeast. TERATOGENIC EFFECTS: Not available. DEVELOPMENTAL TOXICITY: Not available. The substance may be toxic to blood, kidneys, liver, mucous membranes, skin, eyes. -

AHFS Pharmacologic-Therapeutic Classification System
AHFS Pharmacologic-Therapeutic Classification System Abacavir 48:24 - Mucolytic Agents - 382638 8:18.08.20 - HIV Nucleoside and Nucleotide Reverse Acitretin 84:92 - Skin and Mucous Membrane Agents, Abaloparatide 68:24.08 - Parathyroid Agents - 317036 Aclidinium Abatacept 12:08.08 - Antimuscarinics/Antispasmodics - 313022 92:36 - Disease-modifying Antirheumatic Drugs - Acrivastine 92:20 - Immunomodulatory Agents - 306003 4:08 - Second Generation Antihistamines - 394040 Abciximab 48:04.08 - Second Generation Antihistamines - 394040 20:12.18 - Platelet-aggregation Inhibitors - 395014 Acyclovir Abemaciclib 8:18.32 - Nucleosides and Nucleotides - 381045 10:00 - Antineoplastic Agents - 317058 84:04.06 - Antivirals - 381036 Abiraterone Adalimumab; -adaz 10:00 - Antineoplastic Agents - 311027 92:36 - Disease-modifying Antirheumatic Drugs - AbobotulinumtoxinA 56:92 - GI Drugs, Miscellaneous - 302046 92:20 - Immunomodulatory Agents - 302046 92:92 - Other Miscellaneous Therapeutic Agents - 12:20.92 - Skeletal Muscle Relaxants, Miscellaneous - Adapalene 84:92 - Skin and Mucous Membrane Agents, Acalabrutinib 10:00 - Antineoplastic Agents - 317059 Adefovir Acamprosate 8:18.32 - Nucleosides and Nucleotides - 302036 28:92 - Central Nervous System Agents, Adenosine 24:04.04.24 - Class IV Antiarrhythmics - 304010 Acarbose Adenovirus Vaccine Live Oral 68:20.02 - alpha-Glucosidase Inhibitors - 396015 80:12 - Vaccines - 315016 Acebutolol Ado-Trastuzumab 24:24 - beta-Adrenergic Blocking Agents - 387003 10:00 - Antineoplastic Agents - 313041 12:16.08.08 - Selective -

Synthesis, Characterization and Biological Evaluation of New Potentially Active Hydrazones of Naproxen Hydrazide
Available online a t www.derpharmachemica.com Scholars Research Library Der Pharma Chemica, 2015, 7(10):93-101 (http://derpharmachemica.com/archive.html) ISSN 0975-413X CODEN (USA): PCHHAX Synthesis, characterization and biological evaluation of new potentially active hydrazones of naproxen hydrazide Ali H. Abbas 1, Amer N. Elias 2*and Ammar A. Fadhil 3 1Department of Pharmaceutical Chemistry, College of Pharmacy, University of Tikrit, Salah-Aldin, Iraq 2Department of Pharmaceutical Chemistry, College of Pharmacy, University of Baghdad, Baghdad, Iraq 3Department of Pharmacology and Toxicology, College of Pharmacy, University of Baghdad, Baghdad, Iraq _____________________________________________________________________________________________ ABSTRACT To synthesize new hydrazone derivatives of naproxen with enhanced anti-inflammatory activity and devoid the ulcerogenic side effects. Hydrazones were synthesized by conjugation of naproxen hydrazide with seven natural and synthetic aldehyde and ketone by using glacial acetic acid as catalyst. The synthesis has been carried out following simple methodology in excellent isolated yields.The structure of the synthesized derivatives has been characterized by elemental microanalysis (CHN), FTIR Spectroscopy, and other physicochemical properties.The anti- inflammatory activity of the synthesized compounds was evaluated in vivo using the egg-white induced edema model in rats, and the results of the biological assay was found to be comparable to Naproxen in this regard. The synthesizedhydrazone of -

Diclofenac Topical Solution Compared with Oral Diclofenac: a Pooled Safety Analysis
Journal of Pain Research Dovepress open access to scientific and medical research Open Access Full Text Article ORIGINAL RESEARCH Diclofenac topical solution compared with oral diclofenac: a pooled safety analysis Sanford H Roth1 Background: Topical nonsteroidal anti-inflammatory drug (NSAID) formulations, which Philip Fuller2 produce less systemic exposure compared with oral formulations, are an option for the manage- ment of osteoarthritis (OA). However, the overall safety and efficacy of these agents compared 1Arizona Research and Education, Arthritis Laboratory, Arizona State with oral or systemic therapy remains controversial. University, Phoenix, AZ, USA; 2Medical Methods: Two 12-week, double-blind, double-dummy, randomized, controlled, multicenter Affairs, Covidien, Hazelwood, MO, USA studies compared the safety and efficacy profiles of diclofenac topical solution (TDiclo) with oral diclofenac (ODiclo). Each study independently showed that TDiclo had similar efficacy to ODiclo. To compare the safety profiles of TDiclo and ODiclo, a pooled safety analysis was performed for 927 total patients who had radiologically confirmed symptomatic OA of the knee. This pooled analysis included patients treated with TDiclo, containing 45.5% dimethyl sulfoxide (DMSO), and those treated with ODiclo. Safety assessments included monitoring of adverse events (AEs), recording of vital signs, dermatologic evaluation of the study knee, and clinical laboratory evaluation. Results: AEs occurred in 312 (67.1%) patients using TDiclo versus 298 (64.5%) of those tak- ing ODiclo. The most common AE with TDiclo was dry skin at the application site (24.1% vs 1.9% with ODiclo; P , 0.0001). Fewer gastrointestinal (25.4% vs 39.0%; P , 0.0001) and cardiovascular (1.5% vs 3.5%; P = 0.055) AEs occurred with TDiclo compared with ODiclo. -

Dissolution of Cellulose in Dimethyl Sulfoxide. Effect of Thiamine Hydrochloride
Polymer Journal, Vol. 22, No. 12, pp 1101-1103 (1990) SHORT COMMUNICATIONS Dissolution of Cellulose in Dimethyl Sulfoxide. Effect of Thiamine Hydrochloride Yoshihiro SHIGEMASA, Yutaka KISHIMOTO, Hitoshi SASHIWA, and Hiroyuki SAIMOTO Department of Materials Science, Faculty of Engineering, Tottori University, Koyama-cho, Tottori 680, Japan (Received August 2, 1990) KEY WORDS Cellulose / Dimethyl sulfoxide / Paraformaldehyde / Thiamin · HCl / Dissolution of cellulose has long been of paraformaldehyde (Merck Co.), and thia interest to investigators concerned with either min · HCl (Nakarai Tesque, Inc.) were used utilization of cellulose as a renewable resource without further purification. or effective methods to functionalize the In a typical experiment, avicel (1.0 g, polysaccharide. Although cellulose is insoluble 6.2 mmol per glucose residue), PF powder in neutral water and common organic solvent, (3.16 g, 0.1 mol as HCHO), and thiamin · HCl utilization in manufacture has shown that the (0.34 g, 1 mmol) were dispersed in DMSO polysaccharide is soluble in sulfuric acid, ( 100 ml) at room temperature. The mixture was aqueous solutions of zinc chloride, sodium then heated with rapid stirring at 90°C for 3 h. hydroxide, tetraalkylammonium hydroxide, Undissolved materials were removed by and cupric ammonium hydroxide. As an centrifugation (3,500 rpm, 5 min), followed by organic solvent, dimethyl sulfoxide containing washing with DMSO, methanol, and hot H 2O paraformaldehyde (DMSO/PF system) has to remove methylol groups. been found to be an excellent nondegrading The amounts of dissolved cellulose were solvent for cellulose. 1 - 3 In addition, studies estimated on the basis of the amounts of un have been reported on cellulose solvents dissolved cellulose. -

Estonian Statistics on Medicines 2016 1/41
Estonian Statistics on Medicines 2016 ATC code ATC group / Active substance (rout of admin.) Quantity sold Unit DDD Unit DDD/1000/ day A ALIMENTARY TRACT AND METABOLISM 167,8985 A01 STOMATOLOGICAL PREPARATIONS 0,0738 A01A STOMATOLOGICAL PREPARATIONS 0,0738 A01AB Antiinfectives and antiseptics for local oral treatment 0,0738 A01AB09 Miconazole (O) 7088 g 0,2 g 0,0738 A01AB12 Hexetidine (O) 1951200 ml A01AB81 Neomycin+ Benzocaine (dental) 30200 pieces A01AB82 Demeclocycline+ Triamcinolone (dental) 680 g A01AC Corticosteroids for local oral treatment A01AC81 Dexamethasone+ Thymol (dental) 3094 ml A01AD Other agents for local oral treatment A01AD80 Lidocaine+ Cetylpyridinium chloride (gingival) 227150 g A01AD81 Lidocaine+ Cetrimide (O) 30900 g A01AD82 Choline salicylate (O) 864720 pieces A01AD83 Lidocaine+ Chamomille extract (O) 370080 g A01AD90 Lidocaine+ Paraformaldehyde (dental) 405 g A02 DRUGS FOR ACID RELATED DISORDERS 47,1312 A02A ANTACIDS 1,0133 Combinations and complexes of aluminium, calcium and A02AD 1,0133 magnesium compounds A02AD81 Aluminium hydroxide+ Magnesium hydroxide (O) 811120 pieces 10 pieces 0,1689 A02AD81 Aluminium hydroxide+ Magnesium hydroxide (O) 3101974 ml 50 ml 0,1292 A02AD83 Calcium carbonate+ Magnesium carbonate (O) 3434232 pieces 10 pieces 0,7152 DRUGS FOR PEPTIC ULCER AND GASTRO- A02B 46,1179 OESOPHAGEAL REFLUX DISEASE (GORD) A02BA H2-receptor antagonists 2,3855 A02BA02 Ranitidine (O) 340327,5 g 0,3 g 2,3624 A02BA02 Ranitidine (P) 3318,25 g 0,3 g 0,0230 A02BC Proton pump inhibitors 43,7324 A02BC01 Omeprazole -
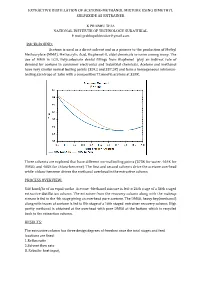
Extractive Distillation of Acetone-Methanol Mixture Using Dimethyl Sulfoxide As Entrainer
EXTRACTIVE DISTILLATION OF ACETONE-METHANOL MIXTURE USING DIMETHYL SULFOXIDE AS ENTRAINER K PRABHU TEJA NATIONAL INSTITUTE OF TECHNOLOGY SURATHKAL E mail:[email protected] BACKGROUND: Acetone is used as a direct solvent and as a pioneer to the production of Methyl Methacrylate (MMA), Methacrylic Acid, Bisphenol-A, aldol chemicals to name among many. The use of MMA in LCD, Polycarbonate dental fillings from Bisphenol play an indirect role of demand for acetone in consumer electronics and industrial chemicals. Acetone and methanol have very similar normal boiling points (329.2 and 337.5K) and form a homogeneous minimum- boiling azeotrope at 1atm with a composition77.6mol% acetone at 328K. Three solvents are explored that have different normal boiling points (373K for water, 464K for DMSO, and 405K for chloro-benzene). The rst and second solvents drive the acetone overhead while chloro-benzene drives the methanol overhead in the extractive column. fi PROCESS OVERVIEW: 540 kmol/hr of an equal-molar Acetone -Methanol mixture is fed to 24th stage of a 36th staged extractive distillation column. The entrainer from the recovery column along with the makeup stream is fed to the 4th stage giving an overhead pure acetone. The DMSO, heavy key(methanol) along with traces of acetone is fed to 8th stage of a 16th staged entrainer recovery column. High purity methanol is obtained at the overhead with pure DMSO at the bottom which is recycled back to the extraction column. RESULTS: The extractive column has three design degrees of freedom once the total stages and feed locations are fixed: 3..Reflux Reboiler ratio heat input. -

Topical Pharmaceutical Compositions of Flurbiprofen and Methyl Salicylate
(19) & (11) EP 2 455 074 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 23.05.2012 Bulletin 2012/21 A61K 31/05 (2006.01) A61K 47/10 (2006.01) A61K 9/00 (2006.01) (21) Application number: 11187973.0 (22) Date of filing: 04.11.2011 (84) Designated Contracting States: • Türkyilmaz, Ali AL AT BE BG CH CY CZ DE DK EE ES FI FR GB 34398 Istanbul (TR) GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO • Akalin, Nur Pehlivan PL PT RO RS SE SI SK SM TR 34398 Istanbul (TR) Designated Extension States: • Önder, Ramazan BA ME 34398 Istanbul (TR) • Öner, Levent (30) Priority: 08.11.2010 TR 201009220 Ankara (TR) (71) Applicant: Sanovel Ilac Sanayi ve Ticaret A.S. (74) Representative: Sevinç, Erkan 34398 Istanbul (TR) Istanbul Patent & Trademark Consultancy Ltd. Plaza-33, Büyükdere cad. No: 33/16, Sisli (72) Inventors: 34381 Istanbul (TR) • Cifter, Ümit 34398 Istanbul (TR) (54) Topical pharmaceutical compositions of flurbiprofen and methyl salicylate (57) The present invention relates to topical pharma- thermore, the invention relates to process for preparing ceutical compositions comprising flurbiprofen or a phar- the said topical pharmaceutical compositions and its use maceutically acceptable salt thereof and methyl sali- for the treatment of pain and inflammatory symptoms as- cylate. More specifically, the invention relates to topical sociated with muscle-skeletol system, joint and soft-tis- pharmaceutical compositions of flurbiprofen and methyl sue disorders. salicylate characterized in that said composition compris- es dimethyl sulfoxide and one or more gelling agent. -

Hierarchical Silica Monolithic Tablets As Novel Carriers for Drug Delivery
European Journal of Pharmaceutics and Biopharmaceutics 141 (2019) 12–20 Contents lists available at ScienceDirect European Journal of Pharmaceutics and Biopharmaceutics journal homepage: www.elsevier.com/locate/ejpb Research paper Hierarchical silica monolithic tablets as novel carriers for drug delivery T ⁎ Wojciech Pudłoa, , Przemysław Borysb, Grzegorz Huszczac, Angelika Staniakc, Renata Zakrzewskad a Department of Chemical Engineering and Process Design, Faculty of Chemistry, Silesian University of Technology, ks. M. Strzody 7, 44-100 Gliwice, Poland b Department of Physical Chemistry and Technology of Polymers, Faculty of Chemistry, Silesian University of Technology, ks. M. Strzody 9, 44-100 Gliwice, Poland c Department of Pharmacy, Pharmaceutical Research Institute, Rydygiera 8, 01-793 Warszawa, Poland d Department of Pharmaceutical Dosage Form Analysis, Pharmaceutical Research Institute, Rydygiera 8, 01-793 Warszawa, Poland ABSTRACT This paper proposes the use of carriers with hierarchical porous structures as novel monolithic tablets for modified drug release. The influence of pore structure on the tamsulosin release profile is presented. The hierarchical arrangement of porous structure in monolithic tablets and the deposition of tamsulosin inside thesilica carrier enable to control the kinetic of release and the amount of tamsulosin released. We developed a mathematical model of tamsulosin release from two carriers with different hierarchy of meso- and macropores. A model of this nature will allow to predict the release of tamsulosin from other carriers withasimilarpore structure. We hope this research will improve the design process of novel carriers, and thus, will allow to tailor the porous structure of a carrier to achieve the desired release profile. 1. Introduction macropores, with diameters of 1–50 μm, and smaller mesopores, with diameters of 2–50 nm, guaranteeing high surface area. -

Opinion on Salicylic Acid (CAS 69-72-7) - Submission I - Corrigendum of 20-21 June 2019
SCCS/1601/18 Final Opinion Corrigendum of 20-21 June 2019 Scientific Committee on Consumer Safety SCCS OPINION ON salicylic acid (CAS 69-72-7) Submission I The SCCS adopted the final Opinion by written procedure on 21 December 2018 Corrigendum of 20-21 June 2019 SCCS/1601/18 Final Opinion Opinion on salicylic acid (CAS 69-72-7) - Submission I - Corrigendum of 20-21 June 2019 ___________________________________________________________________________________________ ACKNOWLEDGMENTS Members of the Working Group are acknowledged for their valuable contribution to this Opinion. The members of the Working Group are: For the preliminary and the final Opinion The SCCS members: Dr U. Bernauer Dr L. Bodin Prof. Q. Chaudhry (SCCS Chair) Prof. P.J. Coenraads (SCCS Vice-Chair and Chairperson of the WG) Prof. M. Dusinska Dr J. Ezendam Dr E. Gaffet Prof. C. L. Galli Dr B. Granum Prof. E. Panteri (Rapporteur) Prof. V. Rogiers (SCCS Vice-Chair) Dr Ch. Rousselle Dr M. Stepnik Prof. T. Vanhaecke Dr S. Wijnhoven External experts: Dr A. Simonnard Dr A. Koutsodimou Prof. W. Uter The additional contribution of the following external expert is gratefully acknowledged: Dr. N. von Goetz All Declarations of Working Group members are available on the following webpage: http://ec.europa.eu/health/scientific_committees/experts/declarations/sccs_en.htm This Opinion has been subject to a commenting period of a minimum eight weeks after its initial publication (from 10 September until 14 November 2018). Comments received during this time were considered by the SCCS. For this Opinion, comments received resulted in the following main changes: sections 3.3.1.1. -

Dimethyl Sulfoxide (DMSO)
Dimethyl Sulfoxide (DMSO) Background Dimethyl Sulfoxide (DMSO) is a hygroscopic solvent and free radical scavenger that has multiple uses in humans and animals.i It is assigned 4/C in the ARCI’s Uniform Classification of Foreign Substances. DMSO has been credited with over 30 pharmacological properties. It can be administered topically, intravenously, intra-articularly, and orally. ii It is most commonly used for primary reduction of inflammation and as a vehicle for percutaneous transport of other therapeutic agents into the body.iii The only FDA- http://web.chem.ucla.edu/~harding/IGOC/D /dmso01.png approved veterinary indication for DMSO is as a topical application to reduce acute swelling due to trauma.iv DMSO has the unique ability to penetrate intact skin and mucous membranes without affecting their integrity. It penetrates cell membranes and micro-organisms and crosses the blood-brain barrier. This permeability allows it to be used to increase the absorption of other drugs through the skin (e.g. corticosteroids). DMSO increases the percutaneous absorption of corticosteroids at least three-fold.v Additionally, DMSO is used for its anti-inflammatory, antibacterial, and antifungal properties. Other effects include provision of analgesia, reduction of platelet aggregation, and a mild cholinesterase-inhibiting effect.vi DMSO has also been used in treating musculoskeletal conditions, neurologic diseases, colic, endotoxemia, reperfusion injury, certain reproductive issues, and most commonly open wounds.vii However, many uses of DMSO lack corresponding well-controlled studies validating its efficacy.viii DMSO is commercially available as a gel and liquid formulation (Domoso™ and generics). ix Both are formulated as 90% by volume and approved for external use only. -

(1.5% W/W Diclofenac Sodium Solution) Topical Anti-Inflammatory
PRODUCT MONOGRAPH Pr Diclofenac Topical Solution (1.5% w/w diclofenac sodium solution) Topical Anti-inflammatory – Analgesic SteriMax Inc. Date of Preparation: 2770 Portland Drive, February 8, 2016 Oakville, ON L6H 6R4 Control No. 166521 1 Pr Diclofenac Topical Solution (1.5% w/w diclofenac sodium solution) PHARMACOLOGIC/THERAPEUTIC CLASSIFICATION Topical Anti-inflammatory – Analgesic ACTIONS AND CLINICAL PHARMACOLOGY Diclofenac sodium is a non-steroidal anti-inflammatory drug (NSAID) of the arylacanoic acid group, with analgesic and anti-inflammatory properties. The mode of action of diclofenac sodium is not fully known, but it is considered to be primarily through its inhibitory effects on prostaglandin synthesis by interfering with the action of prostaglandin synthetase/cyclo- oxygenase, isoforms 1 and 2 (COX-1 and COX-2). It does not act through the pituitary-adrenal axis. Diclofenac sodium does not alter the course of the underlying disease in patients with osteoarthritis; it has been found to relieve pain, reduce swelling and tenderness, and increase mobility. CLINICAL TRIALS Randomized clinical trials with diclofenac sodium solution have NOT been designed to detect differences in cardiovascular adverse events in a chronic setting. However, large population-based observational studies, meta-analyses and systematic reviews suggest that diclofenac use is associated with an increased risk of cardiovascular thrombotic events, including myocardial infarction and ischemic stroke. Results of some studies suggest that the cardiovascular risk is related to the dose and duration of diclofenac exposure and is greater in patients with risk factors for cardiovascular disease. 2 Study 1 In an 84-day (12-week), double-blind, vehicle-controlled clinical trial in patients with osteoarthritis of the knee, the efficacy of diclofenac sodium solution was demonstrated by three primary variables—pain and physical function, as measured with the WOMAC LK3.1 Osteoarthritis Index—plus Patient Global Assessment.