Artificial Intelligence for All Vs. All Conjunction Screening
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Astrodynamics
Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities -

A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star. -

Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature -
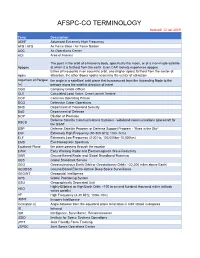
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance -

Use of MESSENGER Radioscience Data to Improve Planetary Ephemeris and to Test General Relativity
A&A 561, A115 (2014) Astronomy DOI: 10.1051/0004-6361/201322124 & © ESO 2014 Astrophysics Use of MESSENGER radioscience data to improve planetary ephemeris and to test general relativity A. K. Verma1;2, A. Fienga3;4, J. Laskar4, H. Manche4, and M. Gastineau4 1 Observatoire de Besançon, UTINAM-CNRS UMR6213, 41bis avenue de l’Observatoire, 25000 Besançon, France e-mail: [email protected] 2 Centre National d’Études Spatiales, 18 avenue Édouard Belin, 31400 Toulouse, France 3 Observatoire de la Côte d’Azur, GéoAzur-CNRS UMR7329, 250 avenue Albert Einstein, 06560 Valbonne, France 4 Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, 77 Av. Denfert-Rochereau, 75014 Paris, France Received 24 June 2013 / Accepted 7 November 2013 ABSTRACT The current knowledge of Mercury’s orbit has mainly been gained by direct radar ranging obtained from the 60s to 1998 and by five Mercury flybys made with Mariner 10 in the 70s, and with MESSENGER made in 2008 and 2009. On March 18, 2011, MESSENGER became the first spacecraft to orbit Mercury. The radioscience observations acquired during the orbital phase of MESSENGER drastically improved our knowledge of the orbit of Mercury. An accurate MESSENGER orbit is obtained by fitting one-and-half years of tracking data using GINS orbit determination software. The systematic error in the Earth-Mercury geometric positions, also called range bias, obtained from GINS are then used to fit the INPOP dynamical modeling of the planet motions. An improved ephemeris of the planets is then obtained, INPOP13a, and used to perform general relativity tests of the parametrized post-Newtonian (PPN) formalism. -

Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution Jeremiah A
Air Force Institute of Technology AFIT Scholar Theses and Dissertations Student Graduate Works 3-24-2016 Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution Jeremiah A. Specht Follow this and additional works at: https://scholar.afit.edu/etd Part of the Information Security Commons, and the Space Vehicles Commons Recommended Citation Specht, Jeremiah A., "Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution" (2016). Theses and Dissertations. 451. https://scholar.afit.edu/etd/451 This Thesis is brought to you for free and open access by the Student Graduate Works at AFIT Scholar. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of AFIT Scholar. For more information, please contact [email protected]. POINTING ANALYSIS AND DESIGN DRIVERS FOR LOW EARTH ORBIT SATELLITE QUANTUM KEY DISTRIBUTION THESIS Jeremiah A. Specht, 1st Lt, USAF AFIT-ENY-MS-16-M-241 DEPARTMENT OF THE AIR FORCE AIR UNIVERSITY AIR FORCE INSTITUTE OF TECHNOLOGY Wright-Patterson Air Force Base, Ohio DISTRIBUTION STATEMENT A. APPROVED FOR PUBLIC RELEASE; DISTRIBUTION UNLIMITED. The views expressed in this thesis are those of the author and do not reflect the official policy or position of the United States Air Force, Department of Defense, or the United States Government. This material is declared a work of the U.S. Government and is not subject to copyright protection in the United States. AFIT-ENY-MS-16-M-241 POINTING ANALYSIS AND DESIGN DRIVERS FOR LOW EARTH ORBIT SATELLITE QUANTUM KEY DISTRIBUTION THESIS Presented to the Faculty Department of Aeronautics and Astronautics Graduate School of Engineering and Management Air Force Institute of Technology Air University Air Education and Training Command In Partial Fulfillment of the Requirements for the Degree of Master of Science in Space Systems Jeremiah A. -

SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS
www.myreaders.info www.myreaders.info Return to Website SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS RC Chakraborty (Retd), Former Director, DRDO, Delhi & Visiting Professor, JUET, Guna, www.myreaders.info, [email protected], www.myreaders.info/html/orbital_mechanics.html, Revised Dec. 16, 2015 (This is Sec. 5, pp 164 - 192, of Orbital Mechanics - Model & Simulation Software (OM-MSS), Sec 1 to 10, pp 1 - 402.) OM-MSS Page 164 OM-MSS Section - 5 -------------------------------------------------------------------------------------------------------43 www.myreaders.info SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS Satellite Ephemeris is Expressed either by 'Keplerian elements' or by 'State Vectors', that uniquely identify a specific orbit. A satellite is an object that moves around a larger object. Thousands of Satellites launched into orbit around Earth. First, look into the Preliminaries about 'Satellite Orbit', before moving to Satellite Ephemeris data and conversion utilities of the OM-MSS software. (a) Satellite : An artificial object, intentionally placed into orbit. Thousands of Satellites have been launched into orbit around Earth. A few Satellites called Space Probes have been placed into orbit around Moon, Mercury, Venus, Mars, Jupiter, Saturn, etc. The Motion of a Satellite is a direct consequence of the Gravity of a body (earth), around which the satellite travels without any propulsion. The Moon is the Earth's only natural Satellite, moves around Earth in the same kind of orbit. (b) Earth Gravity and Satellite Motion : As satellite move around Earth, it is pulled in by the gravitational force (centripetal) of the Earth. Contrary to this pull, the rotating motion of satellite around Earth has an associated force (centrifugal) which pushes it away from the Earth. -

Orbital Mechanics
Danish Space Research Institute Danish Small Satellite Programme DTU Satellite Systems and Design Course Orbital Mechanics Flemming Hansen MScEE, PhD Technology Manager Danish Small Satellite Programme Danish Space Research Institute Phone: 3532 5721 E-mail: [email protected] Slide # 1 FH 2001-09-16 Orbital_Mechanics.ppt Danish Space Research Institute Danish Small Satellite Programme Planetary and Satellite Orbits Johannes Kepler (1571 - 1630) 1st Law • Discovered by the precision mesurements of Tycho Brahe that the Moon and the Periapsis - Apoapsis - planets moves around in elliptical orbits Perihelion Aphelion • Harmonia Mundi 1609, Kepler’s 1st og 2nd law of planetary motion: st • 1 Law: The orbit of a planet ia an ellipse nd with the sun in one focal point. 2 Law • 2nd Law: A line connecting the sun and a planet sweeps equal areas in equal time intervals. 3rd Law • 1619 came Keplers 3rd law: • 3rd Law: The square of the planet’s orbit period is proportional to the mean distance to the sun to the third power. Slide # 2 FH 2001-09-16 Orbital_Mechanics.ppt Danish Space Research Institute Danish Small Satellite Programme Newton’s Laws Isaac Newton (1642 - 1727) • Philosophiae Naturalis Principia Mathematica 1687 • 1st Law: The law of inertia • 2nd Law: Force = mass x acceleration • 3rd Law: Action og reaction • The law of gravity: = GMm F Gravitational force between two bodies F 2 G The universal gravitational constant: G = 6.670 • 10-11 Nm2kg-2 r M Mass af one body, e.g. the Earth or the Sun m Mass af the other body, e.g. the satellite r Separation between the bodies G is difficult to determine precisely enough for precision orbit calculations. -

THE BINARY COLLISION APPROXIMATION: Iliiilms BACKGROUND and INTRODUCTION Mark T
O O i, j / O0NF-9208146--1 DE92 040887 Invited paper for Proceedings of the International Conference on Computer Simulations of Radiation Effects in Solids, Hahn-Meitner Institute Berlin Berlin, Germany August 23-28 1992 The submitted manuscript has been authored by a contractor of the U.S. Government under contract No. DE-AC05-84OR214O0. Accordingly, the U S. Government retains a nonexclusive, royalty* free licc-nc to publish or reproduce the published form of uiii contribution, or allow othen to do jo, for U.S. Government purposes." THE BINARY COLLISION APPROXIMATION: IliiilMS BACKGROUND AND INTRODUCTION Mark T. Robinson >._« « " _>i 8 « g i. § 8 " E 1.2 .§ c « •o'c'lf.S8 ° °% as SOLID STATE DIVISION OAK RIDGE NATIONAL LABORATORY Managed by MARTIN MARIETTA ENERGY SYSTEMS, INC. Under Contract No. DE-AC05-84OR21400 § g With the ••g ^ U. S. DEPARTMENT OF ENERGY OAK RIDGE, TENNESSEE August 1992 'g | .11 DISTRIBUTION OP THIS COOL- ::.•:•! :•' !S Ui^l J^ THE BINARY COLLISION APPROXIMATION: BACKGROUND AND INTRODUCTION Mark T. Robinson Solid State Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831-6032, U. S. A. ABSTRACT The binary collision approximation (BCA) has long been used in computer simulations of the interactions of energetic atoms with solid targets, as well as being the basis of most analytical theory in this area. While mainly a high-energy approximation, the BCA retains qualitative significance at low energies and, with proper formulation, gives useful quantitative information as well. Moreover, computer simulations based on the BCA can achieve good statistics in many situations where those based on full classical dynamical models require the most advanced computer hardware or are even impracticable. -

A Delta-V Map of the Known Main Belt Asteroids
Acta Astronautica 146 (2018) 73–82 Contents lists available at ScienceDirect Acta Astronautica journal homepage: www.elsevier.com/locate/actaastro A Delta-V map of the known Main Belt Asteroids Anthony Taylor *, Jonathan C. McDowell, Martin Elvis Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA, USA ARTICLE INFO ABSTRACT Keywords: With the lowered costs of rocket technology and the commercialization of the space industry, asteroid mining is Asteroid mining becoming both feasible and potentially profitable. Although the first targets for mining will be the most accessible Main belt near Earth objects (NEOs), the Main Belt contains 106 times more material by mass. The large scale expansion of NEO this new asteroid mining industry is contingent on being able to rendezvous with Main Belt asteroids (MBAs), and Delta-v so on the velocity change required of mining spacecraft (delta-v). This paper develops two different flight burn Shoemaker-Helin schemes, both starting from Low Earth Orbit (LEO) and ending with a successful MBA rendezvous. These methods are then applied to the 700,000 asteroids in the Minor Planet Center (MPC) database with well-determined orbits to find low delta-v mining targets among the MBAs. There are 3986 potential MBA targets with a delta- v < 8kmsÀ1, but the distribution is steep and reduces to just 4 with delta-v < 7kms-1. The two burn methods are compared and the orbital parameters of low delta-v MBAs are explored. 1. Introduction [2]. A running tabulation of the accessibility of NEOs is maintained on- line by Lance Benner3 and identifies 65 NEOs with delta-v< 4:5kms-1.A For decades, asteroid mining and exploration has been largely dis- separate database based on intensive numerical trajectory calculations is missed as infeasible and unprofitable. -

TLE-Tools's Documentation!
TLE-tools Release 0.2.3 Federico Stra May 24, 2020 CONTENTS: 1 Purpose 3 2 Installation 5 3 Links 7 4 Indices and tables 9 4.1 API Documentation...........................................9 Python Module Index 15 Index 17 i ii TLE-tools, Release 0.2.3 TLE-tools is a small library to work with two-line element set files. CONTENTS: 1 TLE-tools, Release 0.2.3 2 CONTENTS: CHAPTER ONE PURPOSE The purpose of the library is to parse TLE sets into convenient TLE objects, load entire TLE set files into pandas. DataFrame’s, convert TLE objects into poliastro.twobody.orbit.Orbit’s, and more. From Wikipedia: A two-line element set (TLE) is a data format encoding a list of orbital elements of an Earth-orbiting object for a given point in time, the epoch. The TLE data representation is specific to the simplified perturbations models (SGP, SGP4, SDP4, SGP8 and SDP8), so any algorithm using a TLE as a data source must implement one of the SGP models to correctly compute the state at a time of interest. TLEs can describe the trajectories only of Earth-orbiting objects. Here is an example TLE: ISS (ZARYA) 1 25544U 98067A 19249.04864348.00001909 00000-0 40858-40 9990 2 25544 51.6464 320.1755 0007999 10.9066 53.2893 15.50437522187805 Here is a minimal example on how to load the previous TLE: from tletools import TLE tle_string= """ ISS (ZARYA) 1 25544U 98067A 19249.04864348 .00001909 00000-0 40858-4 0 9990 2 25544 51.6464 320.1755 0007999 10.9066 53.2893 15.50437522187805 """ tle_lines= tle_string.strip().splitlines() t= TLE.from_lines( *tle_lines) Then t is: TLE(name='ISS (ZARYA)', norad='25544', classification='U', int_desig='98067A', epoch_year=2019, epoch_day=249.04864348, dn_o2=1.909e-05, ddn_o6=0.0, bstar=4.0858e- ,!05, set_num=999, inc=51.6464, raan=320.1755, ecc=0.0007999, argp=10.9066,M=53.2893, n=15.50437522, rev_num=18780) and you can then access its attributes like t.argp, t.epoch.. -

FEEDBACK and BRIGHTEST CLUSTER GALAXY FORMATION: ACS OBSERVATIONS of the RADIO GALAXY TN J1338�1942 at Z =4.11 Andrew W
The Astrophysical Journal, 630:68–81, 2005 September 1 # 2005. The American Astronomical Society. All rights reserved. Printed in U.S.A. FEEDBACK AND BRIGHTEST CLUSTER GALAXY FORMATION: ACS OBSERVATIONS OF THE RADIO GALAXY TN J1338À1942 AT z =4.11 Andrew W. Zirm,2 R. A. Overzier,2 G. K. Miley,2 J. P. Blakeslee,3 M. Clampin,4 C. De Breuck,5 R. Demarco,3 H. C. Ford,3 G. F. Hartig,6 N. Homeier,3 G. D. Illingworth,7 A. R. Martel,3 H. J. A. Ro¨ttgering,2 B. Venemans,2 D. R. Ardila,3 F. Bartko,8 N. Benı´tez,9 R. J. Bouwens,6 L. D. Bradley,3 T. J. Broadhurst,10 R. A. Brown,6 C. J. Burrows,6 E. S. Cheng,11 N. J. G. Cross,12 P. D. Feldman,3 M. Franx,2 D. A. Golimowski,3 T. Goto,3 C. Gronwall,13 B. Holden,6 L. Infante,14 R. A. Kimble,4 J. E. Krist,15 M. P. Lesser,16 S. Mei,3 F. Menanteau,3 G. R. Meurer,3 V. Motta,14 M. Postman,3 P. Rosati,5 M. Sirianni,3 W. B. Sparks,3 H. D. Tran,17 Z. I. Tsvetanov,3 R. L. White,3 and W. Zheng3 Receivedv 2005 February 15; accepted 2005 May 11 ABSTRACT We present deep optical imaging of the z ¼ 4:1 radio galaxy TN J1338À1942, obtained using the Advanced Camera for Surveys (ACS) on board the Hubble Space Telescope, as well as ground-based near-infrared imaging data from the European Southern Observatory (ESO) Very Large Telescope (VLT).