Chapter 21 the IS-LM Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Welfare Economic Foundation of Hoarding Loss by Money Circulation Optimization
Munich Personal RePEc Archive Welfare economic foundation of hoarding loss by money circulation optimization Miura, Shinji Independent 13 August 2018 Online at https://mpra.ub.uni-muenchen.de/88443/ MPRA Paper No. 88443, posted 20 Aug 2018 10:07 UTC Welfare economic foundation of hoarding loss by money circulation optimization Shinji Miura (Independent. Gifu, Japan) Abstract Saving brings an economic loss. This is one of the basic propositions of the under-consumption theory. This paper aims to give a welfare economic foundation of this proposition through an optimization method considering money circulation in the case where a type of saving is limited to hoarding. If price is fixed, a non-hoarding state is a necessary condition for Pareto efficiency. However, individual agents who prefer future expenditure hoard money, thus individual rational behavior brings about a Pareto inefficient state. This irrationality of rationality occurs because of a qualitative difference of the budget constraint between the whole society and an individual agent. The former’s constraint incorporates a truth that hoarding decreases other’s revenue, whereas the latter’s does not. Selfish individual agents make a decision with an ignorance of this relational truth because their interest is limited to their private range. As a result, agents fall into an irrational situation despite their rational judgment. Keywords: Money Circulation, Welfare Economics, Under-Consumption, Paradox of Thrift, Intertemporal Choice. 1. Introduction Saving brings an economic loss even though it is often regarded as a virtue. This proposition, known as the paradox of thrift, is one of main elements of the under-consumption theory. -

What Have We Learned? Macroeconomic Policy After the Crisis
What Have We Learned? What Have We Learned? Macroeconomic Policy after the Crisis edited by George Akerlof, Olivier Blanchard, David Romer, and Joseph Stiglitz The MIT Press Cambridge, Massachusetts London, England © 2014 International Monetary Fund and Massachusetts Institute of Technology All rights reserved. No part of this book may be reproduced in any form by any elec- tronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher. Nothing contained in this book should be reported as representing the views of the IMF, its Executive Board, member governments, or any other entity mentioned herein. The views expressed in this book belong solely to the authors. MIT Press books may be purchased at special quantity discounts for business or sales promotional use. For information, please email [email protected]. This book was set in Sabon by Toppan Best-set Premedia Limited, Hong Kong. Printed and bound in the United States of America. Library of Congress Cataloging-in-Publication Data What have we learned ? : macroeconomic policy after the crisis / edited by George Akerlof, Olivier Blanchard, David Romer, and Joseph Stiglitz. pages cm Includes bibliographical references and index. ISBN 978-0-262-02734-2 (hardcover : alk. paper) 1. Monetary policy. 2. Fiscal policy. 3. Financial crises — Government policy. 4. Economic policy. 5. Macroeconomics. I. Akerlof, George A., 1940 – HG230.3.W49 2014 339.5 — dc23 2013037345 10 9 8 7 6 5 4 3 2 1 Contents Introduction: Rethinking Macro Policy II — Getting Granular 1 Olivier Blanchard, Giovanni Dell ’ Ariccia, and Paolo Mauro Part I: Monetary Policy 1 Many Targets, Many Instruments: Where Do We Stand? 31 Janet L. -
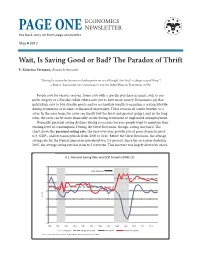
The Paradox of Thrift
ECONOMICS PAGE ONE NEWSLETTER the back story on front page economics May I 2012 Wait, Is Saving Good or Bad? The Paradox of Thrift E. Katarina Vermann, Research Associate “[Saving] is a paradox because in kindergarten we are all taught that thrift is always a good thing.”1 —Paul A. Samuelson, first American to win the Nobel Prize in Economics (1970) People save for various reasons. Some save with a specific purchase in mind, such as cos- metic surgery or a Porsche, while others save just to have more money. Economists say that individuals save to buy durable goods and/or accumulate wealth to maintain a certain lifestyle during retirement or in times of financial uncertainty. These reasons all confer benefits to a saver. In the near term, the saver can finally buy the latest and greatest gadget, and in the long term, the saver can be more financially secure during retirement or unplanned unemployment. Normally, personal saving declines during recessions because people want to maintain their existing level of consumption. During the Great Recession, though, saving increased. The chart shows the personal saving rate, the year-over-year growth rate of gross domestic prod- uct (GDP), and recession periods from 2000 to 2011. Before the Great Recession, the average saving rate for the typical American household was 2.9 percent. Since the recession started in 2007, the average saving rate has risen to 5.0 percent. This increase was largely driven by uncer- Source: Bureau of Economic Analysis, Naonal Bureau of Economic Research, and FRED. Recession Average Saving Rate GDP Growth Personal Saving Rate 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2011 -6 -4 -2 0 Percent 2 4 6 Great Recession 8 U.S. -

The New Paradox of Thrift: Financialisation, Retirement Protection, and Income Polarisation in Hong Kong
China Perspectives 2014/1 | 2014 Post-1997 Hong Kong The New Paradox of Thrift: Financialisation, retirement protection, and income polarisation in Hong Kong Kim Ming Lee, Benny Ho-pong To and Kar Ming Yu Electronic version URL: http://journals.openedition.org/chinaperspectives/6363 DOI: 10.4000/chinaperspectives.6363 ISSN: 1996-4617 Publisher Centre d'étude français sur la Chine contemporaine Printed version Date of publication: 1 March 2014 Number of pages: 5-14 ISSN: 2070-3449 Electronic reference Kim Ming Lee, Benny Ho-pong To and Kar Ming Yu, « The New Paradox of Thrift: », China Perspectives [Online], 2014/1 | 2014, Online since 01 January 2017, connection on 28 October 2019. URL : http:// journals.openedition.org/chinaperspectives/6363 ; DOI : 10.4000/chinaperspectives.6363 © All rights reserved Special feature China perspectives The New Paradox of Thrift Financialisation, retirement protection, and income polarisation in Hong Kong KIM MING LEE, BENNY HO-PONG TO, AND KAR MING YU ABSTRACT: The Hong Kong SAR government has always been proud of the fact that Hong Kong retains its top ranking in terms of “mar - ket freedom” according to most international rating agencies and think tanks. What the government has been much more reluctant to recognise is that, more than 15 years after the handover, Hong Kong now also tops other developed economies in terms of income ine - quality. The growing inequality is caused, among other things, by worsening poverty among the aged. This paper attempts to provide an updated analysis of income and wealth polarisation in Hong Kong, with a particular focus on the retirement protection policy and old-age poverty. -

Paradoxes Situations That Seems to Defy Intuition
Paradoxes Situations that seems to defy intuition PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Tue, 08 Jul 2014 07:26:17 UTC Contents Articles Introduction 1 Paradox 1 List of paradoxes 4 Paradoxical laughter 16 Decision theory 17 Abilene paradox 17 Chainstore paradox 19 Exchange paradox 22 Kavka's toxin puzzle 34 Necktie paradox 36 Economy 38 Allais paradox 38 Arrow's impossibility theorem 41 Bertrand paradox 52 Demographic-economic paradox 53 Dollar auction 56 Downs–Thomson paradox 57 Easterlin paradox 58 Ellsberg paradox 59 Green paradox 62 Icarus paradox 65 Jevons paradox 65 Leontief paradox 70 Lucas paradox 71 Metzler paradox 72 Paradox of thrift 73 Paradox of value 77 Productivity paradox 80 St. Petersburg paradox 85 Logic 92 All horses are the same color 92 Barbershop paradox 93 Carroll's paradox 96 Crocodile Dilemma 97 Drinker paradox 98 Infinite regress 101 Lottery paradox 102 Paradoxes of material implication 104 Raven paradox 107 Unexpected hanging paradox 119 What the Tortoise Said to Achilles 123 Mathematics 127 Accuracy paradox 127 Apportionment paradox 129 Banach–Tarski paradox 131 Berkson's paradox 139 Bertrand's box paradox 141 Bertrand paradox 146 Birthday problem 149 Borel–Kolmogorov paradox 163 Boy or Girl paradox 166 Burali-Forti paradox 172 Cantor's paradox 173 Coastline paradox 174 Cramer's paradox 178 Elevator paradox 179 False positive paradox 181 Gabriel's Horn 184 Galileo's paradox 187 Gambler's fallacy 188 Gödel's incompleteness theorems -

List of Paradoxes 1 List of Paradoxes
List of paradoxes 1 List of paradoxes This is a list of paradoxes, grouped thematically. The grouping is approximate: Paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only those instances that have been termed paradox by at least one source and which have their own article. Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis. Logic • Barbershop paradox: The supposition that if one of two simultaneous assumptions leads to a contradiction, the other assumption is also disproved leads to paradoxical consequences. • What the Tortoise Said to Achilles "Whatever Logic is good enough to tell me is worth writing down...," also known as Carroll's paradox, not to be confused with the physical paradox of the same name. • Crocodile Dilemma: If a crocodile steals a child and promises its return if the father can correctly guess what the crocodile will do, how should the crocodile respond in the case that the father guesses that the child will not be returned? • Catch-22 (logic): In need of something which can only be had by not being in need of it. • Drinker paradox: In any pub there is a customer such that, if he or she drinks, everybody in the pub drinks. • Paradox of entailment: Inconsistent premises always make an argument valid. • Horse paradox: All horses are the same color. • Lottery paradox: There is one winning ticket in a large lottery. It is reasonable to believe of a particular lottery ticket that it is not the winning ticket, since the probability that it is the winner is so very small, but it is not reasonable to believe that no lottery ticket will win. -

Of the Paradoxes of Thrift and Costs in the Long Run? L´Idia Brochier
A Supermultiplier Stock-Flow Consistent model: the \return" of the paradoxes of thrift and costs in the long run? L´ıdiaBrochier? Abstract Supermultiplier models have been recently brought to the post-Keynesian debate. Yet these models still rely on quite simple economic assumptions, being mostly flow models which omit the financial determinants of autonomous expenditures. Since the output growth rate converges in the long run to the exogenously given growth rate of the \non-capacity creating" autonomous expenditure and the utilization rate moves towards the normal utilization rate, the paradoxes of thrift and costs remain valid only in terms of level effects (average growth rates). The aim of this paper is to investigate whether the core conclusions of supermultiplier models hold in a more complex economic framework. It thus presents a supermultiplier SFC model, in which private business investment is assumed to be completely induced by income while the autonomous expenditure component - in this case consumption out of wealth - becomes endogenous. The results of the numerical simulation experiments suggest that the paradox of thrift can remain valid in terms of growth effects and that a lower profit share can also be associated to a higher accumulation rate, though with a lower profit rate. Keywords: Supermultiplier; SFC model; autonomous expenditures; paradoxes of thrift and costs; growth theories. JEL classification codes: B59, E11, E12, E25, O41. 1 Introduction Supermultiplier models, as originally conceived by Sraffian authors (Serrano, 1995a; Bortis, 1997), keep the Keynesian hypothesis, emphasizing the idea that growth can be demand-led even in the long run. This is made possible through the introduction of a \non capacity creating" autonomous expenditure which grows at an exogenously given rate and towards which capital accumulation rate will converge in the long run, as business invest- ment is completely induced by income. -

Engineering a Paradox of Thrift Recession∗
Engineering a Paradox of Thrift Recession∗ Zhen Huo José-Víctor Ríos-Rull University of Minnesota University of Minnesota Federal Reserve Bank of Minneapolis Federal Reserve Bank of Minneapolis CAERP, CEPR, NBER December 2012 Abstract We build a variation of the neoclassical growth model in which financial shocks to house- holds or wealth shocks (in the sense of wealth destruction) generate recessions. Two standard ingredients that are necessary are (1) the existence of adjustment costs that make the ex- pansion of the tradable goods sector difficult and (2) the existence of some frictions in the labor market that prevent enormous reductions in real wages (Nash bargaining in Mortensen- Pissarides labor markets is enough). We pose a new ingredient that greatly magnifies the recession: a reduction in consumption expenditures reduces measured productivity, while technology is unchanged due to reduced utilization of production capacity. Our model pro- vides a novel, quantitative theory of the current recessions in southern Europe. Keywords: Great Recession, Paradox of thrift, Endogenous productivity JEL classifications: E20, E32, F44 ∗Ríos-Rull thanks the National Science Foundation for Grant SES-1156228. We are thankful for discussions with Yan Bai, Kjetil Storesletten, and Nir Jaimovich and the comments of Joan Gieseke and of the attendants at the many seminars where this paper was presented. The views expressed herein are those of the authors and not necessarily those of the Federal Reserve Bank of Minneapolis or the Federal Reserve System. 1 Introduction We develop a model in which recessions are triggered by the desire of households to save more (i.e., because of insufficient demand), and we map our model to a standard modern economy. -

Secular Stagnation: Facts, Causes and Cures Rates and Extraordinary Central Bank Manoeuvres
e Six years after the Global Crisis, the recovery is still anaemic despite years of near-zero interest Secular Stagnation: Facts, Causes and Cures rates and extraordinary central bank manoeuvres. Is ‘secular stagnation’ to blame? Secular Stagnation: This eBook gathers the thinking of leading economists including Larry Summers, Paul Krugman, Robert Gordon, Olivier Blanchard, Richard Koo, Barry Eichengreen, Ricardo Caballero, Ed Facts, Causes and Cures Glaeser and a dozen others. A fairly strong consensus emerged on four points. • Secular stagnation (SecStag) means that negative real interest rates are needed to equate saving and investment at full-employment output levels. • The key worry is that SecStag will make it hard to achieve full employment with low Edited by Coen Teulings and inflation and financial stability using macroeconomic policy as it is currently structured Richard Baldwin and operated. • It is too early to tell whether secular stagnation is to blame, but uncertainty is not an excuse for inaction. Policymakers should start thinking about solutions; if secular stagnation sets in, today’s toolkit will be inadequate. • Europe has more to fear from the possibility of secular stagnation than the US, given its slower overall growth and its lack of pro-growth reforms and more constrained policy framework. The authors point to two classes of solutions: ‘Prevention’ (raising long-run growth potentials) and ‘symptomatic treatment’ (raising the inflation target to alleviate the zero lower bound problem, and using fiscal policy to -

Paradox of Thrift Recessions
NBER WORKING PAPER SERIES PARADOX OF THRIFT RECESSIONS Zhen Huo José-Víctor Ríos-Rull Working Paper 19443 http://www.nber.org/papers/w19443 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 September 2013 Ríos-Rull thanks the National Science Foundation for Grant SES-1156228. We are thankful to Mark Aguiar and Francois Gourio for discussing this paper, and for discussions with George Alessandria, Yan Bai, Christopher Carroll, Oleg Itskhoki, Nir Jaimovich, Greg Kaplan, Patrick Kehoe, Pete Klenow, and Kjetil Storesletten, as well as the comments of Joan Gieseke and the attendants at the many seminars where this paper was presented. The views expressed herein are those of the authors and not necessarily those of the Federal Reserve Bank of Minneapolis, the Federal Reserve System, or the National Bureau of Economic Research. NBER working papers are circulated for discussion and comment purposes. They have not been peer- reviewed or been subject to the review by the NBER Board of Directors that accompanies official NBER publications. © 2013 by Zhen Huo and José-Víctor Ríos-Rull. All rights reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit, including © notice, is given to the source. Paradox of Thrift Recessions Zhen Huo and José-Víctor Ríos-Rull NBER Working Paper No. 19443 September 2013 JEL No. E00,E2,E32 ABSTRACT We build a variation of the neoclassical growth model in which both wealth shocks (in the sense of wealth destruction) -

NBER Reporter NATIONAL BUREAU of ECONOMIC RESEARCH
NBER Reporter NATIONAL BUREAU OF ECONOMIC RESEARCH Reporter OnLine at: www.nber.org/reporter 2013 Number 1 Program Report IN THIS ISSUE Program Report Labor Studies Labor Studies 1 Research Summaries David Card* “Understanding Financial Crises” 5 “The Age of Mass Migration” 9 Saving in Developing Countries 12 “Climate Change and Biofuel Mandates” 15 The Labor Studies (LS) Program is one of the largest and most active in the NBER, with almost 150 members producing nearly 200 Working Papers each year. The breadth of topics and expertise is stun- NBER Profiles 18 ning: it ranges from cutting edge research on aggregate labor market Conferences 20 issues like unemployment and productivity to the effects of govern- NBER News 23 ment programs like Disability Insurance, the differences in labor mar- Program and Working Group Meetings 27 ket outcomes among different educational, gender, and racial groups, Bureau Books 31 and to many other topics in social science. Reflecting their diversity, two-thirds of program members are affiliated with at least one other NBER program, and in the past few years the Labor Studies program has convened joint sessions at the NBER’s Summer Institute with Public Economics, Economics of Education, Economics of Children, and with Working Groups in Personnel Economics and the Economics of Crime. This summer we will add a new joint session with Development Economics. In this report I briefly summarize some of the main themes emerg- ing from recent work by LS affiliates in three areas: immigration, gen- der, and unemployment. These topics barely scratch the surface of the vast body of work by LS affiliates, but give a flavor of some of the emerging ideas and latest techniques in the field. -

The Case for a Consumed Income Tax Structure Robert Leeson [email protected] 2 September 2010-11Am9 Presented to UWO Abstrac
The Case for a Consumed Income Tax Structure Robert Leeson [email protected] 2nd September 2010-11am9 Presented to UWO Abstract This paper extends the case for a Consumed Income Tax Structure (CITS). The first five components of the case are traditional: it encourages growth, offers flexibility and simplification and introduces some much-needed rationality into the tax system. But the CITS also relates to a deeper definition of income (as final satisfaction, not the receipt of money in return for services rendered); it provides the tax system with a much-needed ethical foundation; it liberates the labor supply/leisure choice from all tax-based distortions, returning the surplus to those to whom it belongs (the worker and the employer); and it helps dissolve societal conflicts by providing a consensus-foundation for the mixed economy. When CITS is embedded in a progressive system, it collects increasing units of marginal taxation from diminishing units of marginal utility (the Paradox of Flat Progressivity). Taxation ceases to be a compulsory levy on socially worthwhile activities and becomes entirely a voluntary donation. CITS thus collects taxes through an invisible hand; it also assists the invisible hand of what Adam Smith called the “impartial spectator” to provide both privately and socially optimal levels of savings. It reduces the incentive to evade and facilitates an increase in future consumption through increased savings (the Non-Paradox of Thrift). Under CITS, Veblen’s snobs would help balance the budget. The Introductory Casei Agreement will never be reached about the optimal size and reach of government: at the margin, value judgments will always dominate.