DOCSLIB.ORG

Problems in Elementary Mathematics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Problems in Elementary Mathematics PROBLEMS IN ELEMENTARY MATHEMATICS MIR PUBLISHERS MOSCOW 3AAA 4l9 B. B..NACKIIA, IIO 3JIEMEHTAPHOf1 A.B OBCRHHHKOB, A.H. TYJIAAKOB. MATEMATHKE M. H WABYHHH H3.1 ATE.BbCTBO 4HAYKA. MOCKBA V. LIDSKY, PROBLEMS L. OVSYANNIKOV, A. TULAIKOV, M. SHABUNIN IN ELEMENTARY MATHEMATICS MIR PUBLISHERSI MOSCOW UDC 511+512+513+514(0.75.4)=20 Translated frori the Russian by V. VOLOSOV First published 1973 Revised from the 1970 Russian edition Ha axaau1cxoet R3btKe Q English translation, Mir Publishers, 1973 0223 - 374 041(01) - 73 CONTENTS ProblemsSolutions Algebra 1. Arithmetic and Geometric Progressions (1-23) 7 87 2. AlgebraicEquations and Systems ofEquations (24-95) 10 95 3. Algebraic Inequalities (96-123) . 20 134 4. Logarithmic and ExponentialEquations,Identities and Inequalities (124-169) . 24 142 5. Combinatorial Analysis and Newton's Binomial Theorem (170-188) . 29 157 6. Problems in Forming Equations (189-228) . 32 162 7. Miscellaneous Problems (229-291) ....... .. .. 38 180 Geometry A. Plane Geometry 1. Computation Problems (292-324).. .......... 47 202 2. Construction Problems (325.338) . ....... 51 217 3. Proof Problems (339-408) . .... 52 223 4. Loci of Points (409-420). ... ... 59 254 5. The Greatest and Least Values (421-430).. ...... 61 260 B. Solid Geometry 1. Computation Problems (431-500) . ........... 62 266 2. Proof Problems (501-523) . ... .. 70 309 3. Loci of Points (524-530) . .... ... 72 322 4. The Greatest and Least Values (531-532)..... ... 72 325 Trigonometry 1. Transforming Expressions Containing Trigonometric Func- tions (533-554) . 74 327 2. Trigonometric Equations and Systems of Equations (555-618) 77 333 3. Inverse Trigonometric Functions (619628) . .. 82 363 4. Trigonometric Inequalities (629-645) . 83 366 5. Miscellaneous Problems (646-658). ... 85 372 PROBLEMSALGEBRA 1. Arithmetic and Geometric Progressions Preliminaries Let a, d and Sn be, respectively, the nth term, the common difference and the sum of the first n terms of an arithmetic pro- gression. Then an=a1+d(n-1) (1) and Sn- 2 2 (2) Ifu,,,q and S are the nth term, the common ratio and the sum of the first n terms of a geometric progression, then an = ulgn-1 (3) and S= unq-ul = u1(qn- 1) n q-1 q-1 (4) Finally,if S isthe sum of an infinite geometric series with I qI < 1then S= . (5) uql 1. Prove that if positive numbers a, b and c form an arithmetic progression then the numbers 1 I 1 1 14V ' Y+a Ya+Yb also form an arithmetic progression. 2. Positive numbers a,, a2,..., anform an arithmetic progres- sion. Prove that I I I +I +Yan-I+Yan_n-l Ya1+Ya2 a2+Ya3 Ya1+Yan 3. Prove that if numbers a az, .,an are different from zero and form an arithmetic progression then alas a,a2 aaa` alan 8 PROBLEMS IN ELEMENTARY MATHEMATICS 4. Prove that any sequence of numbers a a2,... , ansatisfying the condition I I I I _n-1 -{- --j a-f -.. a1a2 a2a3 asaa an-1an alan for every n > 3 is an arithmetic progression. 5. Prove that for every arithmetic progression a a2, as, ars we have the equalities a, - 2a2 -1- a3 = 0, a,-3a2+3a3-a,=0, a,-4a2+6a3-4a4-{-a;=0; and, generally, a,-CRa2-{ Cna3-...(-l)'-' Cn-lars{ (-1)"Cna0 (where n > 2). Hint. Here and in the problem below it is advisable to apply the identity Cn =Cn_1+Cn-f which can be readily verified. 6. Given an arithmetic progression a... , ars, an+ ... prove that the equalities of -Cna2 '+.. + (-l )" Cqa;+1= 0 hold for n > 3. 7. Prove thatifthe numbers log* x,log. x and logn,x (x 1) form an arithmetic progression then 1'12 =_ (kn) 1091, m. 8. Find an arithmetic progression ifitis known that the ratio of the sum of the first n terms to the sum of the kn subsequent terms is independent of n. 9. The numbers x x2r... ,x, form an arithmetic progression. Find this progression if x, -l" x2 -l- ... +x,=a, xf -l- x2 -l-. .-}- xn = b2. Hint. Here and in the problem below use the equality 12+22 +32-{- ... + n2=n(n+1 )(2n+1) 10. The number sequence 1, 4, 10, 19, ... satisfies the condition that the differences of two subsequent terms form an arithmetic progression.Find the nth term and the sum of the first n terms of this sequence. PROBLEMS ALGEBRA 9 11. Consider the table 1 2, 3, 4 3, 4, 5, 6, 7 4, 5, 6, 7, 8, 9, 10 Prove that the sum of the terms in each row is equal to the square of an odd number. 12. Given the terms an,+n = A and a,n_n = B ofa geometric progression al, a2, a,,... ,find an and an (A 0 0). 13. Let Sn be the sum of the first n terms of a geometric pro- gression (S,0, q / 0). Prove that Sn _S2n-Sn Stn-SnS3n-S2n 14. Knowing the sum S. ofthefirst n terms of a geometric progression and the sum Sn of the reciprocals of these terms find the product nn of the first n terms of the progression. 15. Find the sum 1 +2x-i-3x2-j--4x3+... H-(n+ 16. Find the sum 1+11+111... { 111... 1 if the last summand is an n-digit number. 17. Find the sum nx+(n-1)x2+... +2x"-'+1x". 18. Find the sum 22L } 2 ... + 2"l 19. Prove that the numbers 49, 4489, 444889, ... obtained by inserting 48 into the middle of the preceding number are squares of integers. 20. Construct a geometric progression with Iql < 1 whose every term differs from the sum of all subsequent terms by a given constant factor k. For what values of k is the problem solvable? 10 PROBLEMS IN ELEMENTARY MATHEMATICS 21. An infinite number sequence x,, x2, x3,... , xn, ...(x, 0) satisfies the condition (x1 +X21+ ... +xrt_1) (x2 + x3 + ... -+- xn) _ = (x,x2 + x2x3 + ... -r X. _ lxrs)2 for any n 3. Prove that the numbers x1, x2,... ,x7l,...form an infinite geometric progression. Hint. Use the method of complete induction. 22. Given an arithmetic progression with general term a and a geometric progression with general term b,,. Prove that a < b for n > 2ifa, = b1,a2 = b2,a, r a2 and a > 0 for all natural numbers n. 23. Prove thatifthetermsofa geometric progression a,, a2,... ,a,,, ..and of an arithmetic progression b,, b2,... ,b,,,.. satisfy the inequalities a,>0,a2>0,b2-b1>0 then there exists a number a such that the difference is independent of n. 2. Algebraic Equations and Systems of Equations Preliminaries In the problems below the original systems of equations should be simplified and reduced to equivalent systems whose all solu- tions either are known or can readily be found. In some cases itis necessary to introduce redundant equations which are a priori satisfied by the solutions of the original systems but may have, inthe general case, some extraneous solutions. Then the values of the unknowns thus obtained must be tested by substituting them into the original systems. In some problems one should use Vieta's theorem for the equation of the third degree x3+px2--qx+r=0. (1) The theorem establishes the following relations between the coef- ficients p,q and rof the equation and its roots x1, x2 and x3: x,x2 x1x2x3 = - r. (2) X, + x2 + x3 = - p, 1 x2x3 ± x3x1 = q, Formulas (2)are derived by equating the coefficients in the equal powers of x on both sides of the identity x3 -l- px2 -1- qx -}- r (x-x1) (x-x2) (x-x3). PROBLEMS. ALGEBRA 11 24. Find all real solutions of the system of equations x3+y3=1, xzy+2xya+y3=2. J 25. Solve the system of equations x2+xy+y2=4, x+xy+y=2. 26. Find the real solutions of the system of equations x3+y3 =50, x3y + xy2 = a3 J provided a is real and different from zero. 27. Solve the system of equations xz x=12,y2 Y x+y=s1 1 1 28. Solve the system of equations x4 +x2y2 + y4 91 x2-xy+y2=7. 29. Solve the system of equations x3-y3= 19(x-y), x3+y3=7(x+y). 30. Find all real solutions of the system of equations 2(x+y)=5xy, 8(x3+y3)=65. 31. Find the real solutions of the system of equations (x+y)(x2-y2)=9, , (x-y) (x2+y2)=5. 32. Find all real solutions of the system of equations x+y 1, x4 + y4 = 7. 33. Solve the system of equations x+y 1, xb+y6=31. PROBLEMS IN ELEMENTARY MATHEMATICS 34. Find the real solutions of the system of equations x4+y4-x2y2= 13, x2-y2_-2xy=1, satisfying the condition xy>0. 35. Solve the system of equations (x2+1)(y2+1)=10, (x+y)(xy-1)=3. Hint. Put xy=v and x+y=u. 36. Solve the system of equations (x2+y2) x 6, y (x2 - y2) = 1. 37. Solve the system of equationsz x2 + y2 = axy, x4+ y4 = bx2 38. Solve the equation (x+b)2 (a + F ab )x2-b40 by factorizing its left member. 39. Solve the equation x2 48 x 4 3+x2 101 3 x 40. Solve the system of equations x yy+ x y I 7y-}x_yb b 41. Find all the solutions of the equation (x-4.5)4 + (x-5.5)2 = 1. 42. Solve the system of equations jx-1J-fly-51=1, y=5-i--lx=-l1*. * The absolute value ofa number x (denoted asl x I)is the non-negative number determined by the conditions _-x for x < 0, ixl xfor x:_::- 0.
Load more

Recommended publications
  • Feasibility Study for Teaching Geometry and Other Topics Using Three-Dimensional Printers
    Feasibility Study For Teaching Geometry and Other Topics Using Three-Dimensional Printers Elizabeth Ann Slavkovsky A Thesis in the Field of Mathematics for Teaching for the Degree of Master of Liberal Arts in Extension Studies Harvard University October 2012 Abstract Since 2003, 3D printer technology has shown explosive growth, and has become significantly less expensive and more available. 3D printers at a hobbyist level are available for as little as $550, putting them in reach of individuals and schools. In addition, there are many “pay by the part” 3D printing services available to anyone who can design in three dimensions. 3D graphics programs are also widely available; where 10 years ago few could afford the technology to design in three dimensions, now anyone with a computer can download Google SketchUp or Blender for free. Many jobs now require more 3D skills, including medical, mining, video game design, and countless other fields. Because of this, the 3D printer has found its way into the classroom, particularly for STEM (science, technology, engineering, and math) programs in all grade levels. However, most of these programs focus mainly on the design and engineering possibilities for students. This thesis project was to explore the difficulty and benefits of the technology in the mathematics classroom. For this thesis project we researched the technology available and purchased a hobby-level 3D printer to see how well it might work for someone without extensive technology background. We sent designed parts away. In addition, we tried out Google SketchUp, Blender, Mathematica, and other programs for designing parts. We came up with several lessons and demos around the printer design.
    [Show full text]
  • Elementary Math Program
    North Shore Schools Elementary Mathematics Curriculum Our math program, Math in Focus, is based upon Singapore Math, which places an emphasis on developing proficiency with problem solving while fostering conceptual understanding and fundamental skills. Online resources are available at ThinkCentral using the username and password provided by the classroom teacher. The mathematics curriculum is aligned with the Common Core Learning Standards (CCLS). There are eight Mathematical Practices that set an expectation of understanding of mathematics and are the same for grades K-12. Mathematical Practices 1. Make sense of problems and persevere in 4. Model with mathematics. solving them. 5. Use appropriate tools strategically. 2. Reason abstractly and quantitatively. 6. Attend to precision. 3. Construct viable arguments and critique the 7. Look for and make use of structure. reasoning of others. 8. Look for and express regularity in repeated reasoning. The content at each grade level focuses on specific critical areas. Kindergarten Representing and Comparing Whole Numbers Students use numbers, including written numerals, to represent quantities and to solve quantitative problems, such as counting objects in a set; counting out a given number of objects; comparing sets or numerals; and modeling simple joining and separating situations with sets of objects, or eventually with equations such as 5 + 2 = 7 and 7 – 2 = 5. (Kindergarten students should see addition and subtraction equations, and student writing of equations in kindergarten is encouraged, but it is not required.) Students choose, combine, and apply effective strategies for answering quantitative questions, including quickly recognizing the cardinalities of small sets of objects, counting and producing sets of given sizes, counting the number of objects in combined sets, or counting the number of objects that remain in a set after some are taken away.
    [Show full text]
  • Math for Elementary Teachers
    Math for Elementary Teachers Math 203 #76908 Name __________________________________________ Spring 2020 Santiago Canyon College, Math and Science Division Monday 10:30 am – 1:25 pm (with LAB) Wednesday 10:30 am – 12:35 pm Instructor: Anne Hauscarriague E-mail: [email protected] Office: Home Phone: 714-628-4919 Website: www.sccollege.edu/ahauscarriague (Grades will be posted here after each exam) Office Hours: Mon: 2:00 – 3:00 Tues/Thurs: 9:30 – 10:30 Wed: 2:00 – 4:00 MSC/CraniumCafe Hours: Mon/Wed: 9:30 – 10:30, Wed: 4:00 – 4:30 Math 203 Student Learning Outcomes: As a result of completing Mathematics 203, the student will be able to: 1. Analyze the structure and properties of rational and real number systems including their decimal representation and illustrate the use of a representation of these numbers including the number line model. 2. Evaluate the equivalence of numeric algorithms and explain the advantages and disadvantages of equivalent algorithms. 3. Analyze multiple approaches to solving problems from elementary to advanced levels of mathematics, using concepts and tools from sets, logic, functions, number theory and patterns. Prerequisite: Successful completion of Math 080 (grade of C or better) or qualifying profile from the Math placement process. This class has previous math knowledge as a prerequisite and it is expected that you are comfortable with algebra and geometry. If you need review work, some resources are: School Zone Math 6th Grade Deluxe Edition, (Grade 5 is also a good review of basic arithmetic skills); Schaum’s Outline series Elementary Mathematics by Barnett Rich; www.math.com; www.mathtv.com; and/or www.KhanAcademy.com.
    [Show full text]
  • Elementary Mathematics Framework
    2015 Elementary Mathematics Framework Mathematics Forest Hills School District Table of Contents Section 1: FHSD Philosophy & Policies FHSD Mathematics Course of Study (board documents) …….. pages 2-3 FHSD Technology Statement…………………………………...... page 4 FHSD Mathematics Calculator Policy…………………………….. pages 5-7 Section 2: FHSD Mathematical Practices Description………………………………………………………….. page 8 Instructional Guidance by grade level band …………………….. pages 9-32 Look-for Tool……………………………………………………….. pages 33-35 Mathematical Practices Classroom Visuals……………………... pages 36-37 Section 3: FHSD Mathematical Teaching Habits (NCTM) Description………………………………………………………….. page 38 Mathematical Teaching Habits…………………...……………….. pages 39-54 Section 4: RtI: Response to Intervention RtI: Response to Intervention Guidelines……………………….. pages 55-56 Skills and Scaffolds………………………………………………... page 56 Gifted………………………………………………………………... page 56 1 Section 1: Philosophy and Policies Math Course of Study, Board Document 2015 Introduction A team of professional, dedicated and knowledgeable K-12 district educators in the Forest Hills School District developed the Math Course of Study. This document was based on current research in mathematics content, learning theory and instructional practices. The Ohio’s New Learning Standards and Principles to Actions: Ensuring Mathematical Success for All were the main resources used to guide the development and content of this document. While the Ohio Department of Education’s Academic Content Standards for School Mathematics was the main source of content, additional sources were used to guide the development of course indicators and objectives, including the College Board (AP Courses), Achieve, Inc. American Diploma Project (ADP), the Ohio Board of Regents Transfer Assurance Guarantee (TAG) criteria, and the Ohio Department of Education Program Models for School Mathematics. The Mathematics Course of Study is based on academic content standards that form an overarching theme for mathematics study.
    [Show full text]
  • Chemical Formula
    Chemical Formula Jean Brainard, Ph.D. Say Thanks to the Authors Click http://www.ck12.org/saythanks (No sign in required) AUTHOR Jean Brainard, Ph.D. To access a customizable version of this book, as well as other interactive content, visit www.ck12.org CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook®, CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform®. Copyright © 2013 CK-12 Foundation, www.ck12.org The names “CK-12” and “CK12” and associated logos and the terms “FlexBook®” and “FlexBook Platform®” (collectively “CK-12 Marks”) are trademarks and service marks of CK-12 Foundation and are protected by federal, state, and international laws. Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms. Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution-Non-Commercial 3.0 Unported (CC BY-NC 3.0) License (http://creativecommons.org/ licenses/by-nc/3.0/), as amended and updated by Creative Com- mons from time to time (the “CC License”), which is incorporated herein by this reference.
    [Show full text]
  • Presentation on Key Ideas of Elementary Mathematics
    Key Ideas of Elementary Mathematics Sybilla Beckmann Department of Mathematics University of Georgia Lesson Study Conference, May 2007 Sybilla Beckmann (University of Georgia) Key Ideas of Elementary Mathematics 1/52 US curricula are unfocused A Splintered Vision, 1997 report based on the TIMSS curriculum analysis. US state math curriculum documents: “The planned coverage included so many topics that we cannot find a single, or even a few, major topics at any grade that are the focus of these curricular intentions. These official documents, individually or as a composite, are unfocused. They express policies, goals, and intended content coverage in mathematics and the sciences with little emphasis on particular, strategic topics.” Sybilla Beckmann (University of Georgia) Key Ideas of Elementary Mathematics 2/52 US instruction is unfocused From A Splintered Vision: “US eighth grade mathematics and science teachers typically teach far more topic areas than their counterparts in Germany and Japan.” “The five surveyed topic areas covered most extensively by US eighth grade mathematics teachers accounted for less than half of their year’s instructional periods. In contrast, the five most extensively covered Japanese eighth grade topic areas accounted for almost 75 percent of their year’s instructional periods.” Sybilla Beckmann (University of Georgia) Key Ideas of Elementary Mathematics 3/52 Breaking the “mile-wide-inch-deep” habit Every mathematical skill and concept has some useful application has some connection to other concepts and skills So what mathematics should we focus on? Sybilla Beckmann (University of Georgia) Key Ideas of Elementary Mathematics 4/52 What focus? Statistics and probability are increasingly important in science and in the modern workplace.
    [Show full text]
  • Mathematics (MATH) 1
    Mathematics (MATH) 1 MATH 116Q. Introduction to Cryptology. 1 Unit. Mathematics (MATH) This course gives a historical overview of Cryptology and the mathematics behind it. Cryptology is the science of making (and Courses breaking) secret codes. From the oldest recorded codes (taken from hieroglyphic engravings) to the modern encryption schemes necessary MATH 104Q. Introduction to Logic. 1 Unit. to secure information in a global community, Cryptology has become An introduction to the informal and formal principles, techniques, an intrinsic part of our culture. This course will examine not only the and skills that are necessary for distinguishing correct from incorrect mathematics behind Cryptology, but its cultural and historical impact. reasoning. Offered each semester. Cross-listed as PHIL 104Q. Topics will include: matrix methods for securing data, substitutional MATH 110Q. Elementary Mathematics. 1 Unit. ciphers, transpositional codes, Vigenere ciphers, Data Encryption Elementary mathematics is a content course, not a course in methods Standard (DES), and public key encryption. The mathematics of teaching. The Elementary Mathematics course will explore the encountered as a consequence of the Cryptology schemes studied development of the number system, properties of and operations with will include matrix algebra, modular arithmetic, permutations, statistics, rational numbers; ratio; proportion; percentages; an introduction to real probability theory, and elementary number theory. Offered annually, numbers; elementary algebra; informal geometry and measurement; either fall or spring semester. and introduces probability and descriptive statistics. Offered annually, MATH 122Q. Calculus for Business Decisions. 1 Unit. either fall or spring semester. This course covers tools necessary to apply the science of decision- MATH 111Q. Finite Mathematics.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Examining Curricular Coverage of Volume Measurement: a Comparative Analysis
    International Journal on Social and Education Sciences Volume 2, Issue 1, 2020 ISSN: 2688-7061 (Online) Examining Curricular Coverage of Volume Measurement: A Comparative Analysis Dae S. Hong University of Iowa, United States, [email protected] Kyong Mi Choi University of Virginia, United States Cristina Runnalls California State Polytechnic University, United States Jihyun Hwang University of Iowa, United States Abstract: In this study, we examined and compared volume and volume-related lessons in two common core aligned U.S. textbook series and Korean elementary textbooks. Because of the importance of textbooks in the lesson enactment process, examining what textbooks offer to students and teachers is important. Since different parts of a textbook provide potentially different opportunities to learn (OTL) to students, we examined exposition, worked examples, and exercise problems as these three areas potentially provide OTL to teachers and students. We paid attention to various OTL that textbooks provide to teachers and students, the number of volume and volume-related lessons, students' development, learning challenges in volume measurement and response types. Our results showed that both countries' textbooks only provide limited attention to volume lessons, learning challenges are not well addressed, conceptual items were presented as isolated topics, and students often need to provide just short responses. We also made recommendations to teachers and textbook authors. Keywords: Elementary textbooks, Volume Measurement, United States
    [Show full text]
  • Elementary Math Methods Criswell Fall 2019 Syllabus DUKE
    On-Campus Course Syllabus EDU 315 Math Instructional Methods Fall 2019 Class Information Day and Time: Mondays 7:00-9:30 p.m. Room Number: E 202 Contact Information Instructor Name: Dawna Duke Instructor Email: [email protected] Instructor Phone: 214.532.4889 Instructor Office Hours: n/a Course Description and Prerequisites This course is designed to prepare teacHers to evaluate, plan, and deliver math lessons that are appropriate for learners from early cHildHood to 6th grade as well as assess student math knowledge and skills througH a student-centered, inquiry approacH. Students will be introduced to methods for teacHing all cHildren developmentally appropriate topics in Number and Operations, Algebra, Geometry, Measurement, and Data Analysis and Probability (the five NCTM content Standards & TEKS). (9 clock hours of field experience are required for this course.) Course Objectives 1. Be familiar with the NCTM Principles and Standards for School Mathematics, the Texas Essential Knowledge and Skills, and apply them to mathematics planning and instruction. 2. Be familiar with the Professional Standards for Teaching Mathematics and How they influence teacHing methods. 3. Discuss the current influences on and reform movements aimed at mathematics instruction in American scHools. 4. Plan lessons that Incorporate “Doing” mathematics in the elementary classroom. 5. TeacH in a developmentally appropriate way wHicH reflects a constructivist view of learning. 6. Use problem-solving as a principle instructional strategy wHile designing and selecting effective learning tasks. 7. Use a variety of assessment skills to evaluate student progress in mathematics. Required Textbooks TD: Van de Walle, J. A., K.S.K & Bay-Williams, J.
    [Show full text]
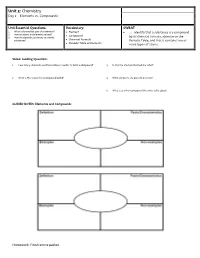
  • Unit 3: Chemistry Day 2 – Elements Vs
    Unit 3: Chemistry Day 2 – Elements vs. Compounds Unit Essential Questions: Vocabulary: SWBAT 1. What is the smallest part of an element? Element … identify that a substance is a compound 2. How are atoms and elements related? Compound 3. How do scientists use density to identify by its chemical formula, absence on the substances? Chemical Formula Periodic Table, and that it contains two or Periodic Table of Elements more types of atoms. Video: Guiding Questions 1. How many elements need to combine in order to form a compound? 3. H2O is the chemical formula for what? 2. What is the recipe for a compound called? 4. What elements are present in water? 5. What is another compound the video talks about? GUIDED NOTES: Elements and Compounds Homework: Finish entire packet. STOP AND JOT: What is the difference between an element and a compound? Chemical Formulas Compounds are represented by _________________________________ _____________________________________. Each capital letter represents _______________ element. ____________________________________ represent the number of atoms of each element. Examples: H2O Si3N4 Number of elements: _____________________ Number of elements: _____________________ Number of atoms for each element: Number of atoms for each element: ______________________ ______________________ ______________________ ________________________ How many elements are in How many atoms of each How many elements are in How many atoms of each the compound H3PO4? element is present in the the compound C2H5OH? element is present in the compound, HNO3? compound, C2H4O2? Three ways to identify a Compound: 1. Made of more than one _________________________. 2. Not located on the _____________________________ __________________________ _________________ ________________________________. 3. Represented by a ____________________________________ ____________________________________.
    [Show full text]
  • E.W. Dijkstra Archive: on the Cruelty of Really Teaching Computing Science
    On the cruelty of really teaching computing science Edsger W. Dijkstra. (EWD1036) http://www.cs.utexas.edu/users/EWD/ewd10xx/EWD1036.PDF The second part of this talk pursues some of the scientific and educational consequences of the assumption that computers represent a radical novelty. In order to give this assumption clear contents, we have to be much more precise as to what we mean in this context by the adjective "radical". We shall do so in the first part of this talk, in which we shall furthermore supply evidence in support of our assumption. The usual way in which we plan today for tomorrow is in yesterday’s vocabulary. We do so, because we try to get away with the concepts we are familiar with and that have acquired their meanings in our past experience. Of course, the words and the concepts don’t quite fit because our future differs from our past, but then we stretch them a little bit. Linguists are quite familiar with the phenomenon that the meanings of words evolve over time, but also know that this is a slow and gradual process. It is the most common way of trying to cope with novelty: by means of metaphors and analogies we try to link the new to the old, the novel to the familiar. Under sufficiently slow and gradual change, it works reasonably well; in the case of a sharp discontinuity, however, the method breaks down: though we may glorify it with the name "common sense", our past experience is no longer relevant, the analogies become too shallow, and the metaphors become more misleading than illuminating.
    [Show full text]