DOCSLIB.ORG

Concept of Force and Newton's Laws of Motion Concept of Force

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Concept of Force and Newton's Laws of Motion Concept of Force Concept of Force G G Force is a vector quantity Fatotal ≡ m The magnitude of the total force is defined to be Concept of Force and F = (mass) x (magnitude of the acceleration) Newton’s Laws of Motion The direction of the total force on a body is the 8.01 same as the direction of the acceleration. W03D1 The SI units for force are newtons (N): 1 N = 1kg . m/s2 Superposition Principle G G Forces Apply two forces and on a body, F1 F2 Gravitation the total force is the vector sum of the two forces: GGG total Electric and magnetic forces FFF=+12 Notation: The force acting on body 1 due to the G Elastic forces (Hooke’s Law) interaction between body 1 and body 2 is denoted by F12 Frictional forces: static and kinetic friction, fluid resistance Example: The total force exerted on Contact forces: normal forces and static m3 by m1 and m2 is: GGG friction total FFF33132=+ Tension and compression 1 Free Body Diagram Newton’s First Law 1. Represent each force that is acting on the object by an arrow on a free body force diagram that indicates the direction of GGG the force T FFF=++⋅⋅⋅12 Every body continues in its state of rest, or of 2. Choose set of independent unit vectors and draw them on uniform motion in a right line, unless it is free body diagram. compelled to change that state by forces G impressed upon it. 3. Decompose each force F in terms of vector components. G i Fijk=++FFFˆˆˆ G G G iixiyiz,,, F0=⇒= vconstant 4. Add vector components to find vector decomposition of the ∑ i total force TTT FFxxx=++⋅⋅⋅1, F 2, TTT FFyyy=1, + F 2, +⋅⋅⋅ TTT FFzzz=++⋅⋅⋅1, F 2, Reference Systems Relatively Inertial Reference Frames Use coordinate system as a ‘reference frame’ to Two reference frames. describe the position, velocity, and acceleration of objects. Origins need not coincide. One moving object has different position vectors in different frames G G G rRr12= + Relative velocity between the two reference frames G G VR= ddt is constant since the relative acceleration is zero G G G AV= ddt= 0 2 Law of Addition of Velocities Newton’s First Law Suppose the object is moving; then, observers in different reference frames will measure different Newton’s First Law in relatively inertial reference velocities frames: If there is no net force impressed on an object at rest in Frame 2, then there is also no G G net force impressed on the object in Frame 1. Velocity of the object in Frame 1: vr11= ddt G G vr= ddt Velocity of the object in Frame 2: 22 An object that is at rest in Frame 2 is moving at a constant velocity in reference Frame 1. Velocity of an object in two different reference GGG frames drrR 12=+ dt dt dt GGG vVv12=+ Table Problem Newton’s Second Law Suppose two cars, Car A, and Car B, are traveling along roads that are perpendicular to The change of motion is proportional to the each other. One observer is at rest with respect motive force impresses, and is made in the direction to the ground. A second observer is in Car A. According to the observer on the ground, Car A of the right line in which that force is impressed, G ˆ G is moving with velocity vj AA = v , and Car B is G G ˆ Fa= m . moving with velocity vi BB = v . What is the velocity of Car B according to the observer in When multiple forces are acting, Car A? Express the velocity of Car B according N G to the observer in Car A as a vector (specify the G ∑Fai = m . components) and give the direction and i=1 magnitude. In Cartesian coordinates: NNN ∑∑∑Fxi,,,===ma x, F yi ma y, F zi ma z. iii===111 3 Newton’s Third Law Force Law: Newtonian Induction To every action there is always opposed an equal • Definition of force has no predictive content. reaction: or, the mutual action of two bodies upon • Need to measure the acceleration and the mass in order to define the each other are always equal, and directed to contrary force. parts. GG • Force Law: Discover experimental relation between force exerted on object and change in properties of object. FF1,2=− 2,1 • Induction: Extend force law from finite measurements to all cases within some range creating a model. • Second Law can now be used to predict motion! Action-reaction pair of forces cannot act on same body; they act on different bodies. • If prediction disagrees with measurement adjust model. Force Law: Gravitational Force Empirical Force Law: Hooke’s near the Surface of the Earth Law Consider a mass m attached to a spring Near the surface of the earth, the gravitational Stretch or compress spring by interaction between a body and the earth is mutually different amounts produces attractive and has a magnitude of G different accelerations Fgrav= mg grav G Hooke’s law: ||F = klΔ m where grav is the gravitational mass of the body and g is a positive constant. −2 Direction: restoring spring to equilibrium g = 9.80665 m ⋅s Hooke’s law holds within some reasonable range of extension or compression 4 Concept Question: Hooke’s Law Two identical springs with spring constant k are attached to each other. A block of mass m is suspended from the lower spring. What is the equivalent spring constant keq of the system of two springs? Note the block displaces Lecture Demo: the same amount in the two Spring Constant figures. 1) keq = k 2) keq = k/2 3) keq = 2k 4) an unknown relation; there is not enough information. Group Problem: Hooke’s Law Force Laws: Contact Forces and Free Body Diagram Between Surfaces The spring in configuration (a) is stretched a The contact force between two surfaces is denoted by the vector distance Δx . The same spring in G G FCtotal ≡ configuration (b) will stretch a distance surface, hand Normal Force: Component of the contact force perpendicular to 1) 2 Δx surface and is denoted by G G 2) Δx normal FN≡ 3) Δx/2 surface, hand Friction Force: Component of the 4) 0 contact force tangent to the surface and is denoted by 5) Not sure G G GGG Fftangent ≡ surface, hand CNf≡+ Therefore the contact force can be modeled as a vector sum 5 Concept Question: Car-Earth Concept Question: Normal Force Interaction Consider a person standing in an elevator that Consider a car at rest. We can conclude that the is accelerating upward. The upward normal downward gravitational pull of Earth on the force N exerted by the elevator floor on the car and the upward contact force of Earth on person is it are equal and opposite because 1) larger than 1) the two forces form an interaction pair. the net force on the car is zero. 2) identical to 2) 3) neither of the above. 3) smaller than 4) unsure the downward force of gravity on the person. Kinetic Friction Static Friction The kinetic frictional force fk is proportional to the Varies in direction and magnitude depending on normal force, but independent of surface area of applied forces: contact and the velocity. 0 ≤ fs ≤ fs,max = μs N The magnitude of fk is Static friction is equal to it’s maximum value fs,max = μs N fk = μk N where µk is the coefficients of friction. Direction of fk: opposes motion 6 Friction on Motorcycle Wheel Tension in a Rope A motorcycle has mass m and is accelerating 1. W μ forwards forwards with 2. Wμ/2 forwards The tension in a rope at a distance x from one end acceleration a. The 3. Wμ backwards of the rope is the magnitude of the action-reaction coefficient of friction of 4. Wμ/2 backwards the rear wheel with the pair of forces acting at that point , 5. Ma forwards road is μ. The weight W G G Ma backwards is equally divided 6. Tx()==FFleft,right () x right,left () x between front and rear 7. Ma/2 forwards wheels. The force of 8. Ma/2 backwards friction on the rear wheel 9. None of above is: Concept Question: Tension in Rope You are trying to pull a rock resting on the ground with a heavy rope (the rope has non-zero mass). Just before the rock slips and starts to move, the magnitude of the tension in the rope is 1) greater than the magnitude of the pulling force? 2) equal to the magnitude of the pulling force? 3) less than the magnitude of the pulling force? 4) Not enough information is given to answer. 7.
Load more

Recommended publications
  • Forces and Motion
    Forces and Motion Forces and motion are very important. You may not know but forces are used in everyday life for example: walking, pushing and pulling. Forces cause things to move. Motion is simply a movement but it needs a force to move. There are two types of forces contact force and non-contact force. Contact force is simply two interacting objects touching for example: throwing a ball. Non-contact force is when two objects are not touching are not touching like the moon and the earth ocean Force Firstly, force is just a technical word push or pull. If you push or pull on an object you are applying a force. Secondly, forces make things move or change their motion. There are so many types of forces here are just a few, gravity and magnetism. Different Forces There are two types of forces. Firstly, there is contact force. This is when two interacting objects are physically touching, for example: throwing a ball, when you throw a ball you use friction to push the pall out of your hands. Secondly, the next force is at a distance force. It is when two interacting objects not touching each other like for example: magnets and a paper clip and the moons gravity and the earth ocean. This occurring because of the gravity and magnetism Contact force Contact force is when you are needing to physically touch another object to allow it to move. There are 4 types of contact forces. Firstly normal force is when nothing is occurring, for example: a book on a table.
    [Show full text]
  • Forces Different Types of Forces
    Forces and motion are a part of your everyday life for example pushing a trolley, a horse pulling a rope, speed and acceleration. Force and motion causes objects to move but also to stay still. Motion is simply a movement but needs a force to move. There are 2 types of forces, contact forces and act at a distance force. Forces Every day you are using forces. Force is basically push and pull. When you push and pull you are applying a force to an object. If you are Appling force to an object you are changing the objects motion. For an example when a ball is coming your way and then you push it away. The motion of the ball is changed because you applied a force. Different Types of Forces There are more forces than push or pull. Scientists group all these forces into two groups. The first group is contact forces, contact forces are forces when 2 objects are physically interacting with each other by touching. The second group is act at a distance force, act at a distance force is when 2 objects that are interacting with each other but not physically touching. Contact Forces There are different types of contact forces like normal Force, spring force, applied force and tension force. Normal force is when nothing is happening like a book lying on a table because gravity is pulling it down. Another contact force is spring force, spring force is created by a compressed or stretched spring that could push or pull. Applied force is when someone is applying a force to an object, for example a horse pulling a rope or a boy throwing a snow ball.
    [Show full text]
  • Electrostatics
    Electrostatics Electrostatics - the study of electrical charges that can be collected and held in one place - charges at rest. Examples: BASIC IDEAS: Electricity begins inside the atom itself. An atom is electrically neutral; it has the same number of protons (+) as it does electrons (-). Objects are charged by adding or removing electrons (charged atom = ion) Fewer electrons than protons = (+) charge occurs More electrons than protons = (-) charge occurs There are two types of charges: positive (+) and negative (-). Like charges repel one another: (+) repels (+), (-) repels (-). Opposite charges attract one another: (+) attracts (-), (-) attracts (+). Charge is quantized Charge is conserved Quantization of Charge The smallest possible amount of charge is that on an electron or proton. This amount is called the fundamental or elementary charge. -19 An electron has charge: qo = -1.602 x 10 C -19 A proton has charge: qo = 1.602 x 10 C Any amount of charge greater than the elementary charge is an exact integer multiple of the elementary charge. q = nqo , where n is an integer For this reason, charge is said to be “quantized”. It comes in quantities of 1.602 x 10-19 C Law of Conservation of Electric Charge The net amount of electric charge produced in any process is zero. Net amount of charge in an isolated system stays constant. Insulators vs. Conductors NOTE: Both insulators and conductors possess charge. Conductor (Metallic Bonds - free valence e’s in outer shell) substance that allows electrons to move easily throughout (sea of electrons) ex. Silver, copper, Al, humid air Insulator (Covalent Bonds - no free e’s in outer shell) substance that does not allow electrons to move freely; electron movement is restricted ex.
    [Show full text]
  • Chapter 6 Space, Time, and the Agent of Interactions Overview
    Chapter 6 Space, Time, and the Agent of Interactions: Overview 35 Chapter 6 Space, Time, and the Agent of Interactions Overview This chapter is somewhat different from the other chapters in this text, in that much of the material serves as reference for the following two chapters. We introduce two new models: The Galilean Space-Time Model, which is the basis for developing a useful way of representing variables that are based on spatial dimensions and time. The second is a model of how “things” interact in our physical universe. Forces are the agents of interactions in this model. It is easy to forget that the common and familiar way we talk about distances, speeds, forces and many other variables using these models are not “the way things really are.” They are only this way in the limited range of applicability of these models, which, fortunately, is sufficiently large to include almost all “everyday” phenomena we experience. But whenever we begin to look too closely at the atomic scale, or at systems in which objects travel near the speed of light, or where there are much larger concentrations of matter than we typically experience in our solar system, our familiar notions of space and time and how forces work have to be replaced. 36 Chapter 6 Space, Time, and the Agent of Interactions: Galilean Model The Galilean Space-Time Model (Summary on foldout #4 at back of text) We live in a world of three spatial dimensions and one time dimension. In our ordinary experience we find that these four dimensions are all independent of each other.
    [Show full text]
  • Surface Forces Surface Forces
    Ch. 6 - Friction Dan Finkenstadt, fi[email protected] October 4, 2015 Surface Forces Surface Forces I Two components of contact force between objects: 1. tangential k, like friction These 2 types of surface force are referred to as 2. and normal ? friction Force { a sideways force that resists the direction of intended travel Normal Force { the outward force that we have already studied I Types of friction Onset of Friction There are also 2 types of friction: static friction fs, which adjusts to applied force kinetic friction fk, which has fixed relation to F~ N Applied Force kinetic friction Friction Coefficients I kinetic friction is a simple function of normal force I fk = µkN fk is the kinetic friction force (lower case) µk is a fraction dependent on materials N is the magnitude of normal force ~f is opposite direction of intended travel Solution: Solution: 7.4 N 0.245 Solution: 2 I Fnet =(10 kg)(2.0 m/s ) = 20 N. I For a frictionless incline: m m g sin θ = (10 kg) (9:8 ) sin 37◦ s2 = 59 N : I ) frictional force is 39 N. Active Learning Exercise Active Learning Exercise Problem: Kinetic Friction Problem: Kinetic Friction A person is pushing a 2:0 kg box along a floor with a force of 10 N A 25.0 kg box rests on a horizontal surface. A at an angle of 30◦ below the horizontal force of 75.0 N is required to set the horizontal. (The box is moving.) box in motion. Once the box is in motion, a The coefficient of kinetic friction horizontal force of 60.0 N is required to keep the between the box and the floor is box in motion at constant speed.
    [Show full text]
  • The Painlevé Paradox in Contact Mechanics Arxiv:1601.03545V1
    The Painlev´eparadox in contact mechanics Alan R. Champneys, P´eterL. V´arkonyi final version 11th Jan 2015 Abstract The 120-year old so-called Painlev´eparadox involves the loss of determinism in models of planar rigid bodies in point contact with a rigid surface, subject to Coulomb-like dry friction. The phenomenon occurs due to coupling between normal and rotational degrees-of-freedom such that the effective normal force becomes attractive rather than repulsive. Despite a rich literature, the forward evolution problem remains unsolved other than in certain restricted cases in 2D with single contact points. Various practical consequences of the theory are revisited, including models for robotic manipulators, and the strange behaviour of chalk when pushed rather than dragged across a blackboard. Reviewing recent theory, a general formulation is proposed, including a Poisson or en- ergetic impact law. The general problem in 2D with a single point of contact is discussed and cases or inconsistency or indeterminacy enumerated. Strategies to resolve the paradox via contact regularisation are discussed from a dynamical systems point of view. By passing to the infinite stiffness limit and allowing impact without collision, inconsistent and inde- terminate cases are shown to be resolvable for all open sets of conditions. However, two unavoidable ambiguities that can be reached in finite time are discussed in detail, so called dynamic jam and reverse chatter. A partial review is given of 2D cases with two points of contact showing how a greater complexity of inconsistency and indeterminacy can arise. Ex- tension to fully three-dimensional analysis is briefly considered and shown to lead to further possible singularities.
    [Show full text]
  • Application of Newton's Second
    Chapter 8 Applications of Newton’s Second Law 8.1 Force Laws ............................................................................................................... 1 8.1.1 Hooke’s Law ..................................................................................................... 1 8.2.2 Principle of Equivalence: ................................................................................ 5 8.2.3 Gravitational Force near the Surface of the Earth ....................................... 5 8.2.4 Electric Charge and Coulomb’s Law ............................................................. 6 Example 8.1 Coulomb’s Law and the Universal Law of Gravitation .................. 7 8.3 Contact Forces ......................................................................................................... 7 8.3.1 Free-body Force Diagram ................................................................................... 9 Example 8.2 Tug-of-War .......................................................................................... 9 8.3.3 Normal Component of the Contact Force and Weight ............................... 11 8.3.4 Static and Kinetic Friction ............................................................................ 14 8.3.5 Modeling ......................................................................................................... 16 8.4 Tension in a Rope .................................................................................................. 16 8.4.1 Static Tension in a Rope ...............................................................................
    [Show full text]
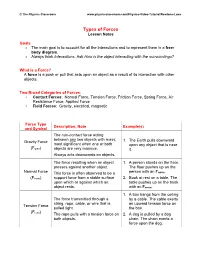
  • Types of Forces Lesson Notes
    © The Physics Classroom www.physicsclassroom.com/Physics-Video-Tutorial/Newtons-Laws Types of Forces Lesson Notes Goals • The main goal is to account for all the interactions and to represent them in a free- body diagram. • Always think Interactions. Ask How is the object interacting with the surroundings? What is a Force? A force is a push or pull that acts upon an object as a result of its interaction with other objects. Two Broad Categories of Forces: • Contact Forces: Normal Force, Tension Force, Friction Force, Spring Force, Air Resistance Force, Applied Force • Field Forces: Gravity, electrical, magnetic Force Type Description, Note Example(s) and Symbol The non-contact force acting between any two objects with mass; Gravity Force 1. The Earth pulls downward most significant when one or both upon any object that is near (Fgrav) objects are very massive. it. Always acts downwards on objects. The force resulting when an object 1. A person stands on the floor. presses against another object. The floor pushes up on the Normal Force This force is often observed to be a person with an Fnorm. (Fnorm) support force from a stable surface 2. Book at rest on a table. The upon which or against which an table pushes up on the book object rests. with an Fnorm. 1. A box hangs from the ceiling The force transmitted through a by a cable. The cable exerts string, rope, cable, or wire that is an upward tension force on Tension Force pulled tight. the box. (F ) tens The rope pulls with a tension force on 2.
    [Show full text]
  • 5-1 Kinetic Friction
    5-1 Kinetic Friction When two objects are in contact, the friction force, if there is one, is the component of the contact force between the objects that is parallel to the surfaces in contact. (The component of the contact force that is perpendicular to the surfaces is the normal force.) Friction tends to oppose relative motion between objects. When there is relative motion, the friction force is the kinetic force of friction. An example is a book sliding across a table, where kinetic friction slows, and then stops, the book. If there is relative motion between objects in contact, the force of friction is the kinetic force of friction (FK). We will use a simple model of friction that assumes the force of kinetic friction is proportional to the normal force. A dimensionless parameter, called the coefficient of kinetic friction, μK, represents the strength of that frictional interaction. F µ = K = µ K so FFKKN . (Equation 5.1: Kinetic friction) FN Some typical values for the coefficient of kinetic friction, as well as for the coefficient of static friction, which we will define in Section 5-2, are given in Table 5.1. The coefficients of friction depend on the materials that the two surfaces are made of, as well as on the details of their interaction. For instance, adding a lubricant between the surfaces tends to reduce the coefficient of friction. There is also some dependence of the coefficients of friction on the temperature. µ µ Interacting materials Coefficient of kinetic friction ( K ) Coefficient of static friction ( S ) Rubber on dry pavement 0.7 0.9 Steel on steel (unlubricated) 0.6 0.7 Rubber on wet pavement 0.5 0.7 Wood on wood 0.3 0.4 Waxed ski on snow 0.05 0.1 Friction in human joints 0.01 0.01 Table 5.1: Approximate coefficients of kinetic friction, and static friction (see Section 5-2), for various interacting materials.
    [Show full text]
  • Lesson Plan Notes Safely
    Contact and Non-Contact Forces Grade 3: Forces Causing Movement Students might need help with Safety cutting skewers or cardboard Lesson Plan Notes safely. Do not swallow magnets. Description In this lesson, students will learn about contact and non-contact forces by building a toy car and moving it with different forces. Materials All of these materials are suggestions of what you could use, you do not need everything on this list. You will need 4 wheels, a body, axles, and a motor. Use what you have and be creative! Toy Car ● Tools ● Body ● Motors ○ Tape ○ craft stick ○ Sheet of paper ○ Scissors ○ foam tray ○ Skewer ○ Pencil ○ cardboard ○ Magnets (stronger the ● 4 Wheels ● Axles better) ○ cardboard ○ Straw ○ Balloon ○ Pop ○ Skewers ○ Plastic straw bottle lids ○ toothpicks (round) Science Background A force is a push or pull caused by objects interacting. Forces are acting on objects all the time. Right now, the force of gravity is pulling you down yet you have not fallen through the floor. What you are sitting on is pushing you up, this is called a normal force. These forces are balanced, so you do not feel or think about them all that much. We notice forces more when they are not balanced which results in objects moving by changing speed or direction. Think of a ball that is sitting in a field. Like us, gravity is pulling it down and the ground is pushing it up. If the ball was kicked, the forces are unbalanced and it goes flying! A kick is a big pushing force that only lasts as long as the contact between the ball and the foot.
    [Show full text]
  • Chap 05H Newton's Laws
    Chapter 5 Newton’s Laws Newton’s Laws • Newton’s First Law • Force & Mass • Newton’s 2nd Law • Contact force: solids, spring & string • Force due to gravity: Weight • Problem solving: Free body diagrams • Newton’s 3rd Law • Problem solving: Two or more objects MFMcGraw - PHY 2425 Chap_05H - Newton - Revised 1/3/2012 2 Newton’s First Law of Motion: Inertia and Equilibrium Newton’s 1 st Law (The Law of Inertia): If no force acts on an object, then the speed and direction of its motion do not change. Inertia is a measure of an object’s resistance to changes in its motion. It is represented by the inertial mass . MFMcGraw - PHY 2425 Chap_05H - Newton - Revised 1/3/2012 3 Newton’s First Law of Motion If the object is at rest, it remains at rest (velocity = 0). If the object is in motion, it continues to move in a straight line with the same velocity. No force is required to keep a body in straight line motion when effects such as friction are negligible. An object is in translational equilibrium if the net force on it is zero and vice versa. Translational Equilibrium MFMcGraw - PHY 2425 Chap_05H - Newton - Revised 1/3/2012 4 Inertial Frame of Reference “If no forces act on an object, any reference frame for which the acceleration of the object remains zero is an inertial reference frame.” -Tipler If the 1st Law is true in your reference frame then you are in an inertial frame of reference. MFMcGraw - PHY 2425 Chap_05H - Newton - Revised 1/3/2012 5 Newton’s Second Law of Motion Net Force, Mass, and Acceleration Newton’s 2nd Law: The acceleration of a body is directly proportional to the net force acting on the body and inversely proportional to the body’s mass.
    [Show full text]
  • 3-6 Exploring Forces and Free-Body Diagrams a Force Is Simply a Push Or a Pull
    Answer to Essential Question 3.5: Even though the Sun is enormous compared to the Earth, Newton’s third law tells us that the force the Sun exerts on the Earth is equal in magnitude, and opposite in direction, to the force the Earth exerts on the Sun. 3-6 Exploring Forces and Free-Body Diagrams A force is simply a push or a pull. A force is a vector, so it has a direction. Also, a force represents an interaction between objects. Let’s build on these facts and learn more about forces. EXPLORATION 3.6A – The normal force Step 1 - Sketch free-body diagrams for the following situations: (a) a book rests on a table; (b) you exert a downward force on the book as it sits on the table; (c) you tie a helium-filled balloon to the book, which remains on the table. The diagrams are shown in Figure 3.13. In (a), the normal force applied by the table on the book has to balance the force of gravity acting on the book. If you push down on the book, the normal force increases – it has to balance the force of gravity as well as the force you exert. Tying a helium balloon to the book reduces the normal force because the normal force and the tension in the string combine to balance the force of gravity. The normal force depends on the situation – the magnitude of the normal force is whatever is Figure 3.13: The upward normal force necessary to prevent the book from falling through the table.
    [Show full text]