Puckering Free Energy of Pyranoses: an NMR and Metadynamics--Umbrella Sampling Investigation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

WO 2013/070444 Al 16 May 2013 (16.05.2013) W P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2013/070444 Al 16 May 2013 (16.05.2013) W P O P C T (51) International Patent Classification: (81) Designated States (unless otherwise indicated, for every A23G 4/00 (2006.01) kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, (21) International Application Number: BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, PCT/US20 12/062043 DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (22) International Filing Date: HN, HR, HU, ID, IL, IN, IS, JP, KE, KG, KM, KN, KP, 26 October 2012 (26.10.2012) KR, KZ, LA, LC, LK, LR, LS, LT, LU, LY, MA, MD, ME, MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, (25) Filing Language: English NO, NZ, OM, PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, (26) Publication Language: English RW, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, (30) Priority Data: ZM, ZW. 61/556,546 7 November 20 11 (07. 11.201 1) US (84) Designated States (unless otherwise indicated, for every (71) Applicant (for all designated States except US): WVI. kind of regional protection available): ARIPO (BW, GH, WRIGLEY JR. COMPANY [US/US]; 1132 Blackhawk GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, SZ, TZ, Street, Chicago, IL 60642 (US). -

Food Carbohydrates: Monosaccharides and Oligosaccharides
Paper No. 01 Paper Title: Food Chemistry Module-04: Food carbohydrates: Monosaccharides and Oligosaccharides Monosaccharides The simplest form of carbohydrates is the monosaccharide. Monosaccharides are either aldoses or ketoses. Aldoses such as glucose consists of a carbon backbone and a carbonyl group (C=O) located at the end of the chain. Ketoses such as fructose consists of a carbon backbone with a carbonyl group located at any other carbon in the chain. The remaining carbon atoms are bound to hydroxyl groups (-OH). Monosaccharide classifications based on the number of carbons Number Category of Examples Name Carbons 4 Tetrose Erythrose, Threose 5 Pentose Arabinose, Ribose, Ribulose, Xylose, Xylulose, Lyxose Allose, Altrose, Fructose, Galactose, Glucose, Gulose, Idose, 6 Hexose Mannose, Sorbose, Talose, Tagatose 7 Heptose Sedoheptulose, Mannoheptulose Monosaccharides Three common sugars glucose, galactose and fructose share the same molecular formula: C6H12O6. Because of their six carbon atoms, each is a hexose. Although all three share the same molecular formula, the arrangement of atoms differs in each case. Substances such as these three, which have identical molecular formulas but different structural formulas, are known as structural isomers. Glucose "Blood sugar" is the immediate source of energy for cellular respiration. Glucose, which is also referred to as dextrose, is a moderately sweet sugar found in vegetables and fruit. When glucose is fermented by the enzyme zymase, in yeast, it results in the formation of carbon dioxide and ethyl alcohol. It is the basic structure to which all carbohydrates are reduced to in the end, for transport via the bloodstream and use by the cells of the body. -
![25 05.Html.Ppt [Read-Only]](https://docslib.b-cdn.net/cover/0806/25-05-html-ppt-read-only-1790806.webp)
25 05.Html.Ppt [Read-Only]
25.5 A Mnemonic for Carbohydrate Configurations The Eight D-Aldohexoses CH O H OH CH2OH The Eight D-Aldohexoses All CH O Altruists Gladly Make Gum In H OH Gallon CH2OH Tanks The Eight D-Aldohexoses All Allose CH O Altruists Altrose Gladly Glucose Make Mannose Gum Gulose In Idose H OH Gallon Galactose CH2OH Tanks Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose Gulose Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose Gulose HO H Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose H OH Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose HO H Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose Gulose HO H Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose H OH Gulose HO H Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose HO H Gulose HO H Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose Mannose H OH Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose Glucose H OH Mannose H OH Gulose H OH Idose H OH Galactose CH2OH Talose The Eight D-Aldohexoses Allose CH O Altrose -
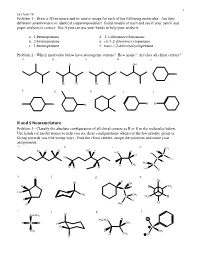
R and S Nomemclature Problem 3 - Classify the Absolute Configuration of All Chiral Centers As R Or S in the Molecules Below
1 Lecture 16 Problem 1 - Draw a 3D structure and its mirror image for each of the following molecules. Are they different (enantiomers) or identical (superimposable)? Build models of each and see if your pencil and paper analysis is correct. See if you can use your hands to help your analysis. a. 1-bromopentane d. 1,1-dibromocyclopentane b. 2-bromopentane e. cis-1,2-dibromocyclopentane c. 3-bromopentane f. trans-1,2-dibromocyclopentane Problem 2 - Which molecules below have stereogenic centers? How many? Are they all chiral centers? a. b. c. d. e. Cl OH Br Br Cl Br Br f. g. h. i. j. Br Br Br Br R and S Nomemclature Problem 3 - Classify the absolute configuration of all chiral centers as R or S in the molecules below. Use hands (or model atoms) to help you see these configurations whenever the low priority group is facing towards you (the wrong way). Find the chiral centers, assign the priorities and make your assignments. a. b. c. d. CH3 Cl H H H3C H H H H3C Br Cl C HO C CH3 I H H3C H CH3 C H H H H3C H e. O f. g. h. H Br Br OH H H H CH3 C H3C CH3 CH3 C H3C H H H H C H Cl 3 i. j. k. l. Cl CH2CH3 Br H3CH2C H C Br H CH3 Cl S CH3 D CH3 H CH3 O H 2 Lecture 16 Pi Bond Priority Problem 4 - Evaluate the order of priority in each part. -

Pyranose Ring Conformation: 1 Pyranose Ring Conformation: 4 #06
#06. 2012-01-20 Quiz 1: Thursday 26 Jan 2012 from 11 AM to 12 noon GG Building Ground Floor #06. 2012-01-20 Last class... Clarification on torsion potential: periodicity 2 and 3 Conformer selection, active/inactive conformations, activation by ligands, etc. - alternative models Inter- and intra-molecular interactions Non-covalent / non-bonded interactions Bonded and non-bonded atoms Hard-sphere approximation Steric effect Preference of trans over gauche conformation for bulky groups #06. 2012-01-20 Monosubstituted cyclohexanes Me Me Bulky group is axially Bulky group is equatorially oriented: gauche to both oriented: trans to both vicinal carbon atoms vicinal carbon atoms #06. 2012-01-20 Monosubstituted cyclohexanes Me Me Bulky group is axially Bulky group is equatorially oriented: gauche to both oriented: trans to both vicinal carbon atoms vicinal carbon atoms #06. 2012-01-20 Cis 1,2-disubstituted cyclohexane Me 4 5 6 Me 3 2 1 #06. 2012-01-20 Trans 1,4-disubstituted cyclohexane 4 5 6 Me Me 3 2 1 #06. 2012-01-20 What governs the conformational preferences? Conformation “a” Conformation “b” Unfolded Folded (protein, DNA, RNA) Monomers (homo/hetero) Oligomer(s) (protein, lipid) A + B A·B (binding) ∆∆∆G = ∆∆∆H – T ∆∆∆S Steric criterion – (approximation of) van der Waals interactions Often, van der Waals contribution is not predominant #06. 2012-01-20 Conformation of 1,3,5-trineopentylbenzene CH 2-tBu tBu-H2C CH 2-tBu Two neopentyl groups are on one side, All the three neopentyl groups are on third on the other side of the ring the same side of the ring view along the plane of the ring Nishio & Hirota (1989) Tetrahedron 45:7201 #06. -

ENZYMATIC HYDROLYSIS of DISACCHARIDES and HALOGENOSALICINS by William Ward Pigman
U. S. DEPARTMENT OF CoMMERCE NATIONAL BUREAU OF STANDARDS RESEARCH PAPER RP1398 Part of Journal of Research of the :National Bureau of Standards, Volume 27, July 1941 ENZYMATIC HYDROLYSIS OF DISACCHARIDES AND HALOGENOSALICINS By William Ward Pigman ABSTRACT In agreement with the Weidenhagen theory, the enzymes of almond emulsin hydrolyze all of the disaccharides with p-glucosidic linkages which have thus far been tried. Measurements of rate of hydrolysis are reported for the first time for gentiobiose, 4-glucosidomannose, and lactositol, and comparable data are as sembled for other disaccharides. It is shown that very small changes in the configuration or structure of the aglucon sugar have a large influence on the rate of enzymatic hydrolysis. This influence is explained on the basis that two areas of the enzyme are involved i,I the adsorption of the disaccharides by the enzyme and that the component nonosaccharide residues are adsorbed separately on the two areas of the enzyme. Rates of enzymatic hydrolysis under the standard conditions of Helferich are reported for the p-chloro-, bromo-, and iodosalicins. It is shown that the intro duction of a halogen in the para position of the salicin aglucon reduces the rate of hydrolysis to less than one-third of the salicin value. While the three halogeno salicins do not differ greatly in their rate of hydrolysis, their relative ease of enzy matic splitting is iodo-> bromo->chloro-. CONTENTS Page I. Introduction____________ ____ _______ ______ _____ ___ ___________ ___ _ 1 II. Discussion of results________________ ____ _____ __ __ ___ __ __________ _ 2 III. -

Process for Producing D-Altrose Verfahren Zur Herstellung Von D-Altrose Procede De Production De D-Altrose
~™ mil mum nun minim (19) J European Patent Office Office europeen des brevets (1 1 ) EP 0 505 573 B1 (12) EUROPEAN PATENT SPECIFICATION (45) Date of publicationation and mention (51) Int. CI.6: C07H 3/02, C07H 19/01 of the grant of the patent: 27.03.1996 Bulletinulletin 1996/13 (86) International application number: PCT/JP91/01376 (21) Application number: 91917514.1 (87) International publication number: WO 92/06986 (30.04.1992 Gazette 1992/10) (22) Date of filing : 09.1 0.1 991 (54) PROCESS FOR PRODUCING D-ALTROSE VERFAHREN ZUR HERSTELLUNG VON D-ALTROSE PROCEDE DE PRODUCTION DE D-ALTROSE (84) Designated Contracting States: (74) Representative: Reinhard - Skuhra - Weise & DE FR GB Partner Postfach 44 01 51 (30) Priority: 12.10.1990 JP 272186/90 D-80750 Munchen (DE) (43) Date of publication of application: (56) References cited: 30.09.1992 Bulletin 1992/40 • CARB. RES. vol. 60 , 1978 pages C11 - C12 J.S. BRIMACOMBE ET AL. 'The stereochemistry of Tobacco Inc. (73) Proprietor: Japan the reduction of 1,6-an hydro-3,4-dideoxy-beta- Shinagawa-ku, Tokyo 140 (JP) D-glycero-hex-3-eno pyranos-2-ulose (levoglucosenone) with lithium aluminium (72) Inventors: hydride' * • MATSUMOTO, Katsuya, • CAN. J. CHEM. vol. 49 1971 pages 1179-1186 Japan Tobacco Inc. , U.P. SINGH ET AL. 'Total Synthesis of alpha,beta- Yokohama-shi, Kanagawa-ken 227 (JP) DL-Allose and alpha, beta-DL-Galactose. • EBATA, Takashi, Stereoselective cis-Hydroxylation by Osmium Tobacco Inc. Japan Tetroxide' * Yokohama-shi, Kanagawa-ken 227 (JP) • ACTA CHEM. SCAND. vol. B34 1 980 page 389 K. -

Characterization of a Thermotolerant ROK-Type Mannofructokinase from Streptococcus Mitis: Application to the Synthesis of Phosphorylated Sugars
Characterization of a thermotolerant ROK-type mannofructokinase from Streptococcus mitis: application to the synthesis of phosphorylated sugars Carine Vergne-Vaxelaire, Aline Mariage, Jean-Louis Petit, Aurélie Fossey-Jouenne, Christine Guérard-Hélaine, Ekaterina Darii, Adrien Debard, Stessy Nepert, Virginie Pellouin, Marielle Lemaire, et al. To cite this version: Carine Vergne-Vaxelaire, Aline Mariage, Jean-Louis Petit, Aurélie Fossey-Jouenne, Christine Guérard- Hélaine, et al.. Characterization of a thermotolerant ROK-type mannofructokinase from Streptococcus mitis: application to the synthesis of phosphorylated sugars. Applied Microbiology and Biotechnology, Springer Verlag, 2018, 102 (13), pp.5569-5583. 10.1007/s00253-018-9018-1. hal-02323767 HAL Id: hal-02323767 https://hal.archives-ouvertes.fr/hal-02323767 Submitted on 22 Oct 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 24/04/2018 e.Proofing Characterization of a thermotolerant ROK-type mannofructokinase from Streptococcus mitis: application to the synthesis of phosphorylated sugars -

Ose: an Editorial on Carbohydrate Nomenclature Neil P
Gly l of cob na io r lo u g o y J Price et al., J Glycobiol 2012, 1:2 Journal of Glycobiology DOI: 10.4172/2168-958X.1000e105 ISSN: 2168-958X Editorial Open Access The Name of the – ose: An Editorial on Carbohydrate Nomenclature Neil P. J. Price* National Center for Agricultural Utilization Research, U.S. Department of Agriculture, Agricultural Research Service, 1815 N. University St., Peoria, IL 61604, USA What’s in a name? The term ‘sugar’ is usually applied to the configuration of theD -aldopentose sugars. Perhaps I can suggest “Ribs monosaccharides, disaccharides, and lower oligosaccharides. Are X-rayed Last” for the series ribose, arabinose, xylose, lyxose, so Historically, sugars were often named after their source, for example, that they also conform to the above rules. grape sugar for glucose, cane sugar for saccharose (later called sucrose), Let’s just take the three most commonly occurring hexose sugars, wood sugar for xylose, and fruit sugar for fructose (fruchtzucker, glucose, galactose, and mannose. The IUPAC name for D-glucose is fructose). The term ‘carbohydrate’ (from the French ‘hydrate de (2R,3S,4R,5R)-6-(hydroxymethyl)tetrahydro-2H-pyran-2,3,4,5-tetrol, carbone’) was originally used only for monosaccharides, because although this is used only rarely. By this nomenclature, D-galactose is their composition can be expressed as C (H O) . Glucose was named n 2 n called (2R,3S,4S,5R)-6-(hydroxymethyl)tetrahydro-2H-pyran-2,3,4,5- in 1838, although much later than this Kekule suggested ‘dextrose’ tetrol and D-mannose is (2S,3S,4R,5R)-6-(hydroxymethyl)tetrahydro- because glucose is dextrorotatory. -

The Carbohydrates
Title The Carbohydrates [C(H2O)]n Emil Hermann Fischer (1852-1919) F-R Convention The Fischer-Rosanoff Convention CHO CHO CHO H OH H OH C2-OH H OH H OH C3-OH H OH H OH C4-OH H OH H OH C5-OH CH2OH CH2OH C6-CH2OH Fischer Projections Rosanoff Modification D/L Series Fischer-Rosanoff D- and L-Series OH on the right of the highest OH on the left of the highest numbered chiral carbon = D-series. numbered chiral carbon = L-series. D-Aldohexoses The D-Aldohexoses C5 8 right C3 2 right 2 left 2 right 2 left C4 4 right 4 left C2 right left right left right left right left Allose Glucose Gulose Galactose Altrose Mannose Idose Talose All altruists gladly make gum in gallon tanks [L. Fieser] Rxn of Aldoses Reactions of Aldoses CHO =N-NHPh CHO HO OH 3 equiv. PhNHNH2 =N-NHPh 3 equiv. PhNHNH2 OH OH OH OH OH HNO3 OH HNO3 OH OH OH osazone NaBH4 NaBH4 CH2OH CH2OH CH2OH Br2/H2O + PhNH2 + NH3 Br2/H2O CO2H CH2OH CO2H CO2H CH2OH CO2H OH OH OH HO HO HO OH OH OH OH OH OH OH OH OH OH OH OH OH OH OH OH OH OH CH2OH CH2OH CO2H CO2H CH2OH CH2OH aldonic acid alditol aldaric acid aldaric acid alditol aldonic acid achiral achiral Osazones More on Osazones CHO CH2OH CHO O Ca(OH)2 OH Ca(OH)2 HO HO HO HO OH OH OH (Lobry de Bruyn- OH OH Alberda van Eckenstein OH rearrangement, 1895) CH2OH CH2OH CH2OH D-glucose D-fructose D-mannose 1 equiv. -

The Long and Winding Road to the Structure of Homo-DNA
TUTORIAL REVIEW www.rsc.org/csr | Chemical Society Reviews The long and winding road to the structure of homo-DNA Martin Egli,*a Paolo Lubinib and Pradeep S. Pallana Received 17th July 2006 First published as an Advance Article on the web 3rd October 2006 DOI: 10.1039/b606807c Homo-DNA ((49A69)-linked oligo-29,39-dideoxy-b-D-glucopyranose nucleic acid) constitutes the earliest synthetic model system whose pairing properties have been studied within an etiology of nucleic acid structure. Its conception as part of a program directed at a rationalization of Nature’s selection of pentoses over other candidates as the carbohydrate building block in the genetic material was motivated by the question: why pentose and not hexose? Homo-DNA forms an autonomous pairing system and its duplexes are entropically stabilized relative to DNA duplexes. Moreover, the base pairing priorities in homo-DNA duplexes differ from those in DNA. A deeper understanding of the particular properties of homo-DNA requires knowledge of its structure. Although diffraction data for crystals of a homo-DNA octamer duplex were available to medium resolution in the mid-1990s, it took another decade for the structure to be solved. In this tutorial Review we describe the odyssey from the crystallization to the final structure determination with its many failures and disappointments and the development of selenium chemistry to derivatize nucleic acids for crystallographic phasing. More than fifty years after the discovery of the DNA double helix, the story of homo-DNA also provides a demonstration of the limits of theoretical models and offers a fresh view of fundamental issues in regard to the natural nucleic acids, such as the origins of antiparallel pairing and helicality. -

Principles of Chemical Nomenclature a GUIDE to IUPAC RECOMMENDATIONS Principles of Chemical Nomenclature a GUIDE to IUPAC RECOMMENDATIONS
Principles of Chemical Nomenclature A GUIDE TO IUPAC RECOMMENDATIONS Principles of Chemical Nomenclature A GUIDE TO IUPAC RECOMMENDATIONS G.J. LEIGH OBE TheSchool of Chemistry, Physics and Environmental Science, University of Sussex, Brighton, UK H.A. FAVRE Université de Montréal Montréal, Canada W.V. METANOMSKI Chemical Abstracts Service Columbus, Ohio, USA Edited by G.J. Leigh b Blackwell Science © 1998 by DISTRIBUTORS BlackweilScience Ltd Marston Book Services Ltd Editorial Offices: P0 Box 269 Osney Mead, Oxford 0X2 0EL Abingdon 25 John Street, London WC1N 2BL Oxon 0X14 4YN 23 Ainslie Place, Edinburgh EH3 6AJ (Orders:Tel:01235 465500 350 Main Street, Maiden Fax: MA 02 148-5018, USA 01235 465555) 54 University Street, Carlton USA Victoria 3053, Australia BlackwellScience, Inc. 10, Rue Casmir Delavigne Commerce Place 75006 Paris, France 350 Main Street Malden, MA 02 148-5018 Other Editorial Offices: (Orders:Tel:800 759 6102 Blackwell Wissenschafts-Verlag GmbH 781 388 8250 KurfUrstendamm 57 Fax:781 388 8255) 10707 Berlin, Germany Canada Blackwell Science KK Copp Clark Professional MG Kodenmacho Building 200Adelaide St West, 3rd Floor 7—10 Kodenmacho Nihombashi Toronto, Ontario M5H 1W7 Chuo-ku, Tokyo 104, Japan (Orders:Tel:416 597-1616 800 815-9417 All rights reserved. No part of Fax:416 597-1617) this publication may be reproduced, stored in a retrieval system, or Australia BlackwellScience Pty Ltd transmitted, in any form or by any 54 University Street means, electronic, mechanical, Carlton, Victoria 3053 photocopying, recording or otherwise, (Orders:Tel:39347 0300 except as permitted by the UK Fax:3 9347 5001) Copyright, Designs and Patents Act 1988, without the prior permission of the copyright owner.