DOCSLIB.ORG

Topic 2 Waveguide and Components

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Topic 2 Waveguide and Components TOPIC 2 WAVEGUIDE AND COMPONENTS COURSE LEARNING OUTCOME (CLO) CLO1 • Explain clearly the generation of microwave, the effects of microwave radiation and the propagation of electromagnetic in a waveguide and its accessories CLO2 • Apply given mathematical equations or Smith Chart to solve problem related to microwave propagation. CLO3 • Handle systematically the related microwave communication equipment in performing the assigned practical work. Understand the characteristic of waveguide Upon completion of this topic, students should be able to: 1. Define a) Critical (cut-off) frequency b) Critical (cut-off) wavelength 2. Explain the following terminologies: Group velocity, Phase velocity, propagation wavelength, waveguide characteristic impedance 3. Calculate the item no.1 and no. 2 for rectangular and circular waveguide Rectangular Waveguide With; a = broad dimension b = narrow dimension x = length waveguide Dimensions of the waveguide which determines the operating frequency range Dimensions of the waveguide which determines the operating frequency range: 1. The size of the waveguide determines its operating frequency range. 2. The frequency of operation is determined by the dimension ‘a’. 3. This dimension is usually made equal to one – half the wavelength at the lowest frequency of operation, this frequency is known as the waveguide cutoff frequency. 4. At the cutoff frequency and below, the waveguide will not transmit energy. At frequencies above the cutoff frequency, the waveguide will propagate energy. Circular waveguide r = radius x = length waveguide Characteristic of waveguide • Waveguides are basically a device ("a guide") for transporting electromagnetic energy from one region to another. • They are capable of directing power precisely to where it is needed, can handle large amounts of power and function as a high-pass filter. • The waveguide acts as a high pass filter in that most of the energy above a certain frequency (the cutoff frequency) will pass through the waveguide, whereas most of the energy that is below the cutoff frequency will be attenuated by the waveguide. Critical (cut-off) Frequency, Fc • The cutoff frequency is the frequency at which all lower frequencies are attenuated by the waveguide, and above the cutoff frequency all higher frequencies propagate within the waveguide. • The cutoff frequency defines the high-pass filter characteristic of the waveguide: above this frequency, the waveguide passes power, below this frequency the waveguide attenuates or blocks power. • The cutoff frequency depends on the shape and size of the cross section of the waveguide. The larger the waveguide is, the lower the cutoff frequency for that waveguide is. The formula for the cutoff frequency of a rectangular cross sectioned waveguide is given by: - permeability - permittivity Rectangular Waveguide • Let us consider a rectangular waveguide with interior dimensions are a x b, • Waveguide can support TE and TM modes. – In TE modes, the electric field is transverse to the direction of propagation. – In TM modes, the magnetic field that is transverse and an electric field component is in the propagation direction. • The order of the mode refers to the field configuration in the guide, and is given by m and n integer subscripts, TEmn and TMmn. – The m subscript corresponds to the number of half- wave variations of the field in the x direction, and – The n subscript is the number of half-wave variations in the y direction. Location of Modes Rectangular Waveguide • A particular mode is only supported above its cutoff frequency. The cutoff frequency is given by 2 2 2 2 1 m n c m n f cmn 22a b a b 8 rr where c 3 10 m/s Rectangular Waveguide Formula Dominant Mode • The dominant mode is the mode with lowest cutoff frequency. • It’s always TE10 • The order of the next modes change depending on the dimensions of the guide. Group and Phase velocity How fast is the wave traveling? • Velocity is a reference distance divided by a reference time. • Group velocity is the velocity at which the energy of the wave propagates. This means that the wave moves at the speed of vg. • Phase velocity is the speed of movement of a point of constant phase in a continous wave. • Group and phase velocities have the same value in free space and in parallel wire transmission lines. Group and Phase velocity The Phase velocity This is the velocity at which the overall shape of the wave’s amplitudes, or the wave ‘envelope’, propagates. (= signal velocity) Here, phase velocity = group velocity (the medium is non- dispersive) Group velocity Dispersion: phase/group velocity depends on frequency Black dot moves at phase velocity. Red dot moves at group velocity. This is normal dispersion (refractive index decreases with increasing λ) Rectangular Waveguide Need to find the fields components of the em wave inside the waveguide Ez Hz Ex Hx Ey Hy We’ll find that waveguides don’t support TEM waves • The m and n represent the mode of propagation and indicates the number of variations of the field in the x and y directions • Note that for the TM mode, if n or m is zero, all fields are zero. Variation of wave impedance • Wave impedance varies with frequency and mode Rectangular Waveguide - Wave Propagation Wave Guide Impedance Wave feature impedance for TE mode is ZTE = 377 2 1 with; 0 • ZTE = characteristic impedance for TE mode • 377 = free space feature impedance • = free space wavelength • 0 = wavelength cut. Wave Guide Impedance Wave feature impedance for TM mode is ZTM = 2 377 1 ( ) 0 where; • ZTM = characteristic impedance for TM mode • 377 = free space feature impedance • = free space wavelength • 0 = wavelength cut. Question Waveguide The circular waveguide is used in many special applications in microwave techniques. It has the advantage of greater power – handling capacity and lower attenuation for a given cutoff wavelength. However, the disadvantage of somewhat greater size and weight. The polarization of the transmitted wave can be altered due to the minor irregularities of the wall surface of the circular guide, whereas the rectangular wave guide the polarization is fixed Description The wave of lowest frequency or the dominant mode in the circular waveguide is the TE11 mode. The first subscript m indicates the number of full – wave variations of the radial component of the electric field around the circumference of the waveguide. The second subscript n indicates the number of half – wave variations across the diameter. The field configurations of TE mode in the circular waveguide is shown in11 the diagram below Applications of circular waveguide Rotating joints in radars to connect the horn antenna feeding a parabolic reflector (which must rotate for tracking) TE01 mode suitable for long distance waveguide transmission above 10 GHz. Short and medium distance broad band communication (could replace / share coaxial and microwave links) • From the cutoff frequencies or the cutoff wavelengths, the phase velocity, the group velocity, the guide wavelength and the wave impedance of each mode can be found using the same equations as those for the rectangular waveguide. Cut Off Wavelength Example 1 Example 2 Solution .
Load more

Recommended publications
  • Frequency Response
    EE105 – Fall 2015 Microelectronic Devices and Circuits Frequency Response Prof. Ming C. Wu [email protected] 511 Sutardja Dai Hall (SDH) Amplifier Frequency Response: Lower and Upper Cutoff Frequency • Midband gain Amid and upper and lower cutoff frequencies ωH and ω L that define bandwidth of an amplifier are often of more interest than the complete transferfunction • Coupling and bypass capacitors(~ F) determineω L • Transistor (and stray) capacitances(~ pF) determineω H Lower Cutoff Frequency (ωL) Approximation: Short-­Circuit Time Constant (SCTC) Method 1. Identify all coupling and bypass capacitors 2. Pick one capacitor ( ) at a time, replace all others with short circuits 3. Replace independent voltage source withshort , and independent current source withopen 4. Calculate the resistance ( ) in parallel with 5. Calculate the time constant, 6. Repeat this for each of n the capacitor 7. The low cut-­off frequency can be approximated by n 1 ωL ≅ ∑ i=1 RiSCi Note: this is an approximation. The real low cut-­off is slightly lower Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier SCTC Method: 1 n 1 fL ≅ ∑ 2π i=1 RiSCi For the Common-Source Amplifier: 1 # 1 1 1 & fL ≅ % + + ( 2π $ R1SC1 R2SC2 R3SC3 ' Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier Using the SCTC method: For C2 : = + = + 1 " 1 1 1 % R3S R3 (RD RiD ) R3 (RD ro ) fL ≅ $ + + ' 2π # R1SC1 R2SC2 R3SC3 & For C1: R1S = RI +(RG RiG ) = RI + RG For C3 : 1 R2S = RS RiS = RS gm Design: How Do We Choose the Coupling and Bypass Capacitor Values? • Since the impedance of a capacitor increases with decreasing frequency, coupling/bypass capacitors reduce amplifier gain at low frequencies.
    [Show full text]
  • Feedback Amplifiers
    UNIT II FEEDBACK AMPLIFIERS & OSCILLATORS FEEDBACK AMPLIFIERS: Feedback concept, types of feedback, Amplifier models: Voltage amplifier, current amplifier, trans-conductance amplifier and trans-resistance amplifier, feedback amplifier topologies, characteristics of negative feedback amplifiers, Analysis of feedback amplifiers, Performance comparison of feedback amplifiers. OSCILLATORS: Principle of operation, Barkhausen Criterion, types of oscillators, Analysis of RC-phase shift and Wien bridge oscillators using BJT, Generalized analysis of LC Oscillators, Hartley and Colpitts’s oscillators with BJT, Crystal oscillators, Frequency and amplitude stability of oscillators. 1.1 Introduction: Feedback Concept: Feedback: A portion of the output signal is taken from the output of the amplifier and is combined with the input signal is called feedback. Need for Feedback: • Distortion should be avoided as far as possible. • Gain must be independent of external factors. Concept of Feedback: Block diagram of feedback amplifier consist of a basic amplifier, a mixer (or) comparator, a sampler, and a feedback network. Figure 1.1 Block diagram of an amplifier with feedback A – Gain of amplifier without feedback. A = X0 / Xi Af – Gain of amplifier with feedback.Af = X0 / Xs β – Feedback ratio. β = Xf / X0 X is either voltage or current. 1.2 Types of Feedback: 1. Positive feedback 2. Negative feedback 1.2.1 Positive Feedback: If the feedback signal is in phase with the input signal, then the net effect of feedback will increase the input signal given to the amplifier. This type of feedback is said to be positive or regenerative feedback. Xi=Xs+Xf Af = = = Af= Here Loop Gain: The product of open loop gain and the feedback factor is called loop gain.
    [Show full text]
  • Unit I Microwave Transmission Lines
    UNIT I MICROWAVE TRANSMISSION LINES INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz radiation or even T-rays.
    [Show full text]
  • Wave Guides & Resonators
    UNIT I WAVEGUIDES & RESONATORS INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz Page 1 radiation or even T-rays.
    [Show full text]
  • Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
    Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels.
    [Show full text]
  • Lab 4: Prelab
    ECE 445 Biomedical Instrumentation rev 2012 Lab 8: Active Filters for Instrumentation Amplifier INTRODUCTION: In Lab 6, a simple instrumentation amplifier was implemented and tested. Lab 7 expanded upon the instrumentation amplifier by improving circuit performance and by building a LabVIEW user interface. This lab will complete the design of your biomedical instrument by introducing a filter into the circuit. REQUIRED PARTS AND MATERIALS: Materials Needed 1) Instrumentation amplifier from Lab 7 2) Results from Prelab 3) Oscilloscope 4) Function Generator 5) DC Power Supply 6) Labivew Software 7) Data Acquisition Board 8) Resistors 9) Capacitors 10) Dual operational amplifier (UA747) PRELAB: 1. Print the Prelab and Lab8 Grading Sheets. Answer all of the questions in the Prelab Grading Sheet and bring the Lab8 Grading Sheet with you when you come to lab. The Prelab Grading Sheet must be turned in to the TA before beginning your lab assignment. 2. Read the LABORATORY PROCEDURE before coming to lab. Note: you are not required to print the lab procedure; you can view it on the PC at your lab bench. 3. For further reading consult class notes, text book and see Low Pass Filters http://www.electronics-tutorials.ws/filter/filter_2.html High Pass Filters http://www.electronics-tutorials.ws/filter/filter_3.html BACKGROUND: Active Filters As their name implies, Active Filters contain active components such as operational amplifiers or transistors within their design. They draw their power from an external power source and use it to boost or amplify the output signal. Operational amplifiers can also be used to shape or alter the frequency response of the circuit by producing a more selective output response by making the output bandwidth of the filter more narrow or even wider.
    [Show full text]
  • DETERMINATION of the APPROPRIATE CUTOFF FREQUENCY in the DIGITAL FILTER DATA SMOOTHING PROCEDURE By
    'DETERMINATION OF THE APPROPRIATE CUTOFF FREQUENCY IN THE DIGITAL FILTER DATA SMOOTHING PROCEDURE by BING YU B.S., Peking Institute of Physical Education, 1982 A MASTER'S THESIS Submitted in partial fulfillment of the requirements for the degree MASTER OF SCIENCE Department of Physical Education and Leisure Studies KANSAS STATE UNIVERSITY 1988 Approved by: Major Professo 3# AllSDfl 5327b7 ']cl ACKNOWLEDGEMENTS The author wishes to acknowledge the assistance and support of the entire graduate faculty of Kansas State University's Department of Physical Education and Leisure Studies. Special thanks go to committee members Dr. Stephan Konz and Dr. Kathleen Williams for their unique perspectives and editorial assistance. Most of all, I would like to thank my major professor, Dr. Larry Noble, for his integrity, his enthusiasm for knowledge, and the tremendous amount of time and assistance he has given me over the past two years. 11 DEDICATION This thesis is dedicated to my parents, Dr. Gou-Rei Yu and Ming-Hua Lu, to my wife Wei Li, to her parents, Dr. Ping Li and Dr. Xiu-Zhang Yu, and to all of the other folks of my family and her family for their understanding of my absence when my son Charlse Alan Yu was born. Their constant support and encouragement are deeply appreciated. 111 . CONTENTS ACKNOWLEDGMENTS ii DEDICATION iii LIST OF FIGURES vi LIST OF TABLES ix Chapter 1 INTRODUCTION 1 Statement Of The Problem 2 Definitions 3 2 REVIEW OF RELATED LITERATURE 7 The Nature Of Errors 7 Sources Of Errors 10 Data Smoothing Techniques Used In Sport Biomechanics 15 Finite difference technique 15 Least square polynomial approxination.
    [Show full text]
  • CP27 Solution
    Electric Circuits Prof. Shayla Sawyer Spring 2015 ECSE 2010 CP27 solution 1) Bode plots/Transfer functions a. Draw magnitude and phase bode plots for the transfer function s⋅() s+ 100 H s()= 0.01 ⋅ ()s+ 1E4 In your magnitude plot, indicate corrections at the poles and zeros. Step 1: Find poles, zeros Zeros: 0, 100 Poles: 1E4 Step 2: Define regions and find either H(j ω) or H(s) 100⋅ 0.01 − 4 = 1× 10 ⋅ 4 s< 100 1 10 0.01⋅ s⋅100 − 4 − 4 H s() = = 1⋅ 10 s +20db/dec slope 100⋅ 1⋅10 = 0.01 4 1⋅ 10 slope ends at 20⋅ log 0.01() −= 40 4 0.01 − 6 100< s < 10 = 1× 10 4 1⋅ 10 0.01⋅ s⋅s − 6 2 H s() = = 1⋅ 10 s 4 +40 db/dec slope 1⋅ 10 2 − 6 4 20log 10 ⋅()1⋅ 10 = 40 4 s> 10 0.01⋅ s⋅s +20db/dec H s() = = 0.01s s slope Step 3: Make corrections Correction at 100 is +3db because it is a ZERO^1! Correction at 10^4 is -3db because it is a POLE^1! 1 Electric Circuits Prof. Shayla Sawyer Spring 2015 ECSE 2010 CP27 solution s2 H ()s = 10 (s +100 )(s +10000 ) Phase plots 0.1 ωc1 = 10 ω = 10 j10⋅() j10+ 100 ∠ 0⋅ ∠90() ∠0() ∠H j10()= 0.01 ⋅ ∠ 90 ()10j+ 1E4 ∠0 ∠0 + ∠90 + ∠0 − ∠0 ⋅ 3 10 ωc1 = 10 3 ω = 10 3 3 3 j10 ⋅()j10 + 100 ∠ 0⋅ ∠90() ∠90() ∠H() j10 = 0.01 ⋅ ∠ 180 3 ∠0 ()10 j+ 1E4 ∠0 + ∠90 + ∠90 − ∠0 180− 45 = 135 2 Electric Circuits Prof.
    [Show full text]
  • Butterworth Filters
    24 Butterworth Filters To illustrate some of the ideas developed in Lecture 23, we introduce in this lecture a simple and particularly useful class of filters referred to as Butter- worthfilters. Filters in this class are specified by two parameters, the cutoff frequency and the filter order. The frequency response of these filters is monotonic, and the sharpness of the transition from the passband to the stop- band is dictated by the filter order. For continuous-time Butterworth filters, the poles associated with the square of the magnitude of the frequency re- sponse are equally distributed in angle on a circle in the s-plane, concentric with the origin and having a radius equal to the cutoff frequency. When the cutoff frequency and the filter order have been specified, the poles character- izing the system function are readily obtained. Once the poles are specified, it is straightforward to obtain the differential equation characterizing the filter. In this lecture, we illustrate the design of a discrete-time filter through the use of the impulse-invariant design procedure applied to a Butterworth filter. The filter specifications are given in terms of the discrete-time frequen- cy variable and then mapped to a corresponding set of specifications for the continuous-time filter. A Butterworth filter meeting these specifications is de- termined. The resulting continuous-time system function is then mapped to the desired discrete-time system function. A limitation on the use of impulse invariance as a design procedure for discrete-time systems is the requirement that the continuous-time filter be bandlimited to avoid aliasing.
    [Show full text]
  • Filter Basics Innovation in Every Wave
    Filter Basics Innovation in Every Wave InnowaveRF, LLC has the knowledge and experience in designing a variety of lumped element filters that are used to satisfy filter requirements from 20Hz to 5GHz. These kinds of filters are also called LC Filters since it consists of discrete elements such as Inductors (L) and Capacitors (C) that are soldered on to a substrate to realize different types of characteristic response. These inductors and capacitors are arranged such that a range of specified frequencies (known as the pass band) passes through with minimal attenuation and rest of the frequencies (known as the reject band / stop band) is attenuated heavily. Lumped element filters can be classified into these four basic categories: Lowpa ss Filters : Highpass Filters : Passes low frequencies, rejects high frequencies Passes high frequencies, rejects low frequencies Bandpass Filters : Bandstop / Band Reject Filters : Passes a band of frequencies centered on a center Rejects a band of frequencies centered on a center frequency, rejects both higher and lower frequencies frequency, passes both higher and lower frequencies 520 White Plains Road, Suite 500, Tarrytown, New York˘10591 • Ph: 914−230−4060 • Fax: 914−819−5656 • www.InnowaveRF.com Filter Basics Innovation in Every Wave Ideal filter will have zero attenuation in the pass band and infinite attenuation in the stop band. However, such a filter cannot be manufactured practically. Using the best design and modeling technique and state-of-the-art CAD solutions, InnowaveRF manufactures filters that have an unloaded Q as high as 400. Along the band edges, the pass band of the filter gets rounded off and then starts the roll-off into the reject band.
    [Show full text]
  • Butterworth Filter Design
    USC Electrical Engineering ELCT 301 Project 44#1 BUTTERWORTH FILTER DESIGN Objective The main purpose of this laboratory exercise is to learn the procedures for designing Butterworth filters. In addition, the theory behind these procedures will be discussed in recitation and the hands-on methods practiced in the laboratory. This exercise will focus on the fourth-order filter but the methods are valid regardless of the order of the filter. In this lab only even order filters will be considered. Background Read pgg.728-738 Hambley and the handout. The Butterworth and Chebyshev filters are high order filter designs which have significantly different characteristics, but both can be realized by using simple first order or biquad stages cascaded together to achieve the desired order, passband response, and cut-off frequency. The Butterworth filter has a maximally flat response, i.e., no passband ripple and a roll-off of -20dB per pole. In the Butterworth scheme the designer is usually optimizing the flatness of the passband response at the expense of roll-off. The Chebyshev filter displays a much steeper roll-off, but the gain in the passband is not constant. The Chebyshev filter is characterized by a significant passband ripple that often can be ignored. The designer in this case is optimizing roll-off at the expense of passband ripple. Both filter types can be implemented using the simple Sallen-Key configuration. The Sallen-Key design (shown in Figure A-1) is a biquadratic or biquad type filter, meaning there are two poles defined by the circuit transfer function H 0 H (s) = 2 , (1) (s /ω0 ) + (1/ Q)(s /ω0 ) + 1 where H0 is the DC gain of the biquad circuit and is a function only of the ratio of the two resistors connected to the negative input of the opamp.
    [Show full text]
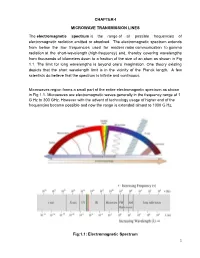
  • CHAPTER-I MICROWAVE TRANSMISSION LINES the Electromagnetic Spectrum Is the Range of All Possible Frequencies of Electromagnetic
    CHAPTER-I MICROWAVE TRANSMISSION LINES The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation emitted or absolved. The electromagnetic spectrum extends from below the low frequencies used for modern radio communication to gamma radiation at the short-wavelength (high-frequency) end, thereby covering wavelengths from thousands of kilometers down to a fraction of the size of an atom as shown in Fig 1.1. The limit for long wavelengths is beyond one‟s imagination. One theory existing depicts that the short wavelength limit is in the vicinity of the Planck length. A few scientists do believe that the spectrum is infinite and continuous. Microwaves region forms a small part of the entire electromagnetic spectrum as shown in Fig 1.1. Microwaves are electromagnetic waves generally in the frequency range of 1 G Hz to 300 GHz. However with the advent of technology usage of higher end of the frequencies became possible and now the range is extended almost to 1000 G Hz. Fig:1.1: Electromagnetic Spectrum 1 Brief history of Microwaves • Modern electromagnetic theory was formulated in 1873 by James Clerk Maxwell, a German scientist solely from mathematical considerations. • Maxwell‟s formulation was cast in its modern form by Oliver Heaviside, during the period 1885 to 1887. • Heinrich Hertz, a German professor of physics carried out a set of experiments during 1887-1891 that completely validated Maxwell‟s theory of electromagnetic waves. • It was only in the 1940‟s (World War II) that microwave theory received substantial interest that led to radar development. • Communication systems using microwave technology began to develop soon after the birth of radar.
    [Show full text]