DOCSLIB.ORG

Fitting Models to Biological Data Using Linear and Nonlinear Regression

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fitting Models to Biological Data Using Linear and Nonlinear Regression Fitting Models to Biological Data using Linear and Nonlinear Regression A practical guide to curve fitting Harvey Motulsky & Arthur Christopoulos Copyright 2003 GraphPad Software, Inc. All rights reserved. GraphPad Prism and Prism are registered trademarks of GraphPad Software, Inc. GraphPad is a trademark of GraphPad Software, Inc. Citation: H.J. Motulsky and A Christopoulos, Fitting models to biological data using linear and nonlinear regression. A practical guide to curve fitting. 2003, GraphPad Software Inc., San Diego CA, www.graphpad.com. To contact GraphPad Software, email [email protected] or [email protected]. Contents at a Glance A. Fitting data with nonlinear regression.................................... 13 B. Fitting data with linear regression..........................................47 C. Models ....................................................................................58 D. How nonlinear regression works........................................... 80 E. Confidence intervals of the parameters ..................................97 F. Comparing models................................................................ 134 G. How does a treatment change the curve?..............................160 H. Fitting radioligand and enzyme kinetics data ....................... 187 I. Fitting dose-response curves .................................................256 J. Fitting curves with GraphPad Prism......................................296 3 Contents Preface ........................................................................................................12 A. Fitting data with nonlinear regression.................................... 13 1. An example of nonlinear regression ......................................................13 Example data ............................................................................................................................13 Step 1: Clarify your goal. Is nonlinear regression the appropriate analysis? .........................14 Step 2: Prepare your data and enter it into the program........................................................15 Step 3: Choose your model.......................................................................................................15 Step 4: Decide which model parameters to fit and which to constrain..................................16 Step 5: Choose a weighting scheme ......................................................................................... 17 Step 6: Choose initial values..................................................................................................... 17 Step 7: Perform the curve fit and interpret the best-fit parameter values ............................. 17 2. Preparing data for nonlinear regression................................................19 Avoid Scatchard, Lineweaver-Burk and similar transforms whose goal is to create a straight line ............................................................................................................................19 Transforming X values ............................................................................................................ 20 Don’t smooth your data........................................................................................................... 20 Transforming Y values..............................................................................................................21 Change units to avoid tiny or huge values .............................................................................. 22 Normalizing ............................................................................................................................. 22 Averaging replicates ................................................................................................................ 23 Consider removing outliers..................................................................................................... 23 3. Nonlinear regression choices ............................................................... 25 Choose a model for how Y varies with X................................................................................. 25 Fix parameters to a constant value? ....................................................................................... 25 Initial values..............................................................................................................................27 Weighting..................................................................................................................................27 Other choices ........................................................................................................................... 28 4. The first five questions to ask about nonlinear regression results ........ 29 Does the curve go near your data? .......................................................................................... 29 Are the best-fit parameter values plausible? .......................................................................... 29 How precise are the best-fit parameter values? ..................................................................... 29 Would another model be more appropriate? ......................................................................... 30 Have you violated any of the assumptions of nonlinear regression? .................................... 30 5. The results of nonlinear regression ...................................................... 32 Confidence and prediction bands ........................................................................................... 32 Correlation matrix ................................................................................................................... 33 Sum-of-squares........................................................................................................................ 33 R2 (Coefficient of Determination)........................................................................................... 34 Does the curve systematically deviate from the data? ........................................................... 35 Could the fit be a local minimum? ...........................................................................................37 6. Troubleshooting “bad” fits.................................................................... 38 Poorly-defined parameters...................................................................................................... 38 Model too complicated ............................................................................................................ 39 4 The model is ambiguous unless you share a parameter .........................................................41 Bad initial values...................................................................................................................... 43 Redundant parameters............................................................................................................45 Tips for troubleshooting nonlinear regression....................................................................... 46 B. Fitting data with linear regression..........................................47 7. Choosing linear regression ................................................................... 47 The linear regression model.....................................................................................................47 Don’t choose linear regression when you really want to compute a correlation coefficient .47 Analysis choices in linear regression ...................................................................................... 48 X and Y are not interchangeable in linear regression ............................................................ 49 Regression with equal error in X and Y .................................................................................. 49 Regression with unequal error in X and Y.............................................................................. 50 8. Interpreting the results of linear regression ......................................... 51 What is the best-fit line?...........................................................................................................51 How good is the fit? ................................................................................................................. 53 Is the slope significantly different from zero? .........................................................................55 Is the relationship really linear? ..............................................................................................55 Comparing slopes and intercepts............................................................................................ 56 How to think about the results of linear regression............................................................... 56 Checklist: Is linear regression the right analysis for these data?............................................57 C. Models ....................................................................................58 9. Introducing models...............................................................................58 What is a model?...................................................................................................................... 58 Terminology............................................................................................................................. 58 Examples of simple models....................................................................................................
Load more

Recommended publications
  • Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A
    IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 9, NO. 6, JUNE 2000 1075 Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A. T. Figueiredo, Member, IEEE, José M. N. Leitão, Member, IEEE, and Anil K. Jain, Fellow, IEEE Abstract—This paper describes a new approach to adaptive having external/potential energy, which is a func- estimation of parametric deformable contours based on B-spline tion of certain features of the image The equilibrium (min- representations. The problem is formulated in a statistical imal total energy) configuration framework with the likelihood function being derived from a re- gion-based image model. The parameters of the image model, the (1) contour parameters, and the B-spline parameterization order (i.e., the number of control points) are all considered unknown. The is a compromise between smoothness (enforced by the elastic parameterization order is estimated via a minimum description nature of the model) and proximity to the desired image features length (MDL) type criterion. A deterministic iterative algorithm is (by action of the external potential). developed to implement the derived contour estimation criterion. Several drawbacks of conventional snakes, such as their “my- The result is an unsupervised parametric deformable contour: it adapts its degree of smoothness/complexity (number of control opia” (i.e., use of image data strictly along the boundary), have points) and it also estimates the observation (image) model stimulated a great amount of research; although most limitations parameters. The experiments reported in the paper, performed of the original formulation have been successfully addressed on synthetic and real (medical) images, confirm the adequacy and (see, e.g., [6], [9], [10], [34], [38], [43], [49], and [52]), non- good performance of the approach.
    [Show full text]
  • Chapter 26: Mathcad-Data Analysis Functions
    Lecture 3 MATHCAD-DATA ANALYSIS FUNCTIONS Objectives Graphs in MathCAD Built-in Functions for basic calculations: Square roots, Systems of linear equations Interpolation on data sets Linear regression Symbolic calculation Graphing with MathCAD Plotting vector against vector: The vectors must have equal number of elements. MathCAD plots values in its default units. To change units in the plot……? Divide your axis by the desired unit. Or remove the units from the defined vectors Use Graph Toolbox or [Shift-2] Or Insert/Graph from menu Graphing 1 20 2 28 time 3 min Temp 35 K time 4 42 Time min 5 49 40 40 Temp Temp 20 20 100 200 300 2 4 time Time Graphing with MathCAD 1 20 Plotting element by 2 28 element: define a time 3 min Temp 35 K 4 42 range variable 5 49 containing as many i 04 element as each of the vectors. 40 i:=0..4 Temp i 20 100 200 300 timei QuickPlots Use when you want to x 0 0.12 see what a function looks like 1 Create a x-y graph Enter the function on sin(x) 0 y-axis with parameter(s) 1 Enter the parameter on 0 2 4 6 x-axis x Graphing with MathCAD Plotting multiple curves:up to 16 curves in a single graph. Example: For 2 dependent variables (y) and 1 independent variable (x) Press shift2 (create a x-y plot) On the y axis enter the first y variable then press comma to enter the second y variable. On the x axis enter your x variable.
    [Show full text]
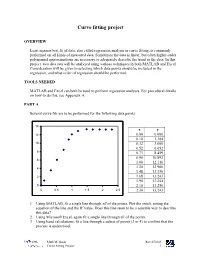
  • Curve Fitting Project
    Curve fitting project OVERVIEW Least squares best fit of data, also called regression analysis or curve fitting, is commonly performed on all kinds of measured data. Sometimes the data is linear, but often higher-order polynomial approximations are necessary to adequately describe the trend in the data. In this project, two data sets will be analyzed using various techniques in both MATLAB and Excel. Consideration will be given to selecting which data points should be included in the regression, and what order of regression should be performed. TOOLS NEEDED MATLAB and Excel can both be used to perform regression analyses. For procedural details on how to do this, see Appendix A. PART A Several curve fits are to be performed for the following data points: 14 x y 12 0.00 0.000 0.10 1.184 10 0.32 3.600 0.52 6.052 8 0.73 8.459 0.90 10.893 6 1.00 12.116 4 1.20 12.900 1.48 13.330 2 1.68 13.243 1.90 13.244 0 2.10 13.250 0 0.5 1 1.5 2 2.5 2.30 13.243 1. Using MATLAB, fit a single line through all of the points. Plot the result, noting the equation of the line and the R2 value. Does this line seem to be a sensible way to describe this data? 2. Using Microsoft Excel, again fit a single line through all of the points. 3. Using hand calculations, fit a line through a subset of points (3 or 4) to confirm that the process is understood.
    [Show full text]
  • SQSTM1 Mutations in Familial and Sporadic Amyotrophic Lateral Sclerosis
    ORIGINAL CONTRIBUTION SQSTM1 Mutations in Familial and Sporadic Amyotrophic Lateral Sclerosis Faisal Fecto, MD; Jianhua Yan, MD, PhD; S. Pavan Vemula; Erdong Liu, MD; Yi Yang, MS; Wenjie Chen, MD; Jian Guo Zheng, MD; Yong Shi, MD, PhD; Nailah Siddique, RN, MSN; Hasan Arrat, MD; Sandra Donkervoort, MS; Senda Ajroud-Driss, MD; Robert L. Sufit, MD; Scott L. Heller, MD; Han-Xiang Deng, MD, PhD; Teepu Siddique, MD Background: The SQSTM1 gene encodes p62, a major In silico analysis of variants was performed to predict al- pathologic protein involved in neurodegeneration. terations in p62 structure and function. Objective: To examine whether SQSTM1 mutations con- Results: We identified 10 novel SQSTM1 mutations (9 tribute to familial and sporadic amyotrophic lateral scle- heterozygous missense and 1 deletion) in 15 patients (6 rosis (ALS). with familial ALS and 9 with sporadic ALS). Predictive in silico analysis classified 8 of 9 missense variants as Design: Case-control study. pathogenic. Setting: Academic research. Conclusions: Using candidate gene identification based on prior biological knowledge and the functional pre- Patients: A cohort of 546 patients with familial diction of rare variants, we identified several novel (n=340) or sporadic (n=206) ALS seen at a major aca- SQSTM1 mutations in patients with ALS. Our findings demic referral center were screened for SQSTM1 muta- provide evidence of a direct genetic role for p62 in ALS tions. pathogenesis and suggest that regulation of protein deg- radation pathways may represent an important thera- Main Outcome Measures: We evaluated the distri- peutic target in motor neuron degeneration. bution of missense, deletion, silent, and intronic vari- ants in SQSTM1 among our cohort of patients with ALS.
    [Show full text]
  • A Toolbox for Nonlinear Regression in R: the Package Nlstools
    JSS Journal of Statistical Software August 2015, Volume 66, Issue 5. http://www.jstatsoft.org/ A Toolbox for Nonlinear Regression in R: The Package nlstools Florent Baty Christian Ritz Sandrine Charles Cantonal Hospital St. Gallen University of Copenhagen University of Lyon Martin Brutsche Jean-Pierre Flandrois Cantonal Hospital St. Gallen University of Lyon Marie-Laure Delignette-Muller University of Lyon Abstract Nonlinear regression models are applied in a broad variety of scientific fields. Various R functions are already dedicated to fitting such models, among which the function nls() has a prominent position. Unlike linear regression fitting of nonlinear models relies on non-trivial assumptions and therefore users are required to carefully ensure and validate the entire modeling. Parameter estimation is carried out using some variant of the least- squares criterion involving an iterative process that ideally leads to the determination of the optimal parameter estimates. Therefore, users need to have a clear understanding of the model and its parameterization in the context of the application and data consid- ered, an a priori idea about plausible values for parameter estimates, knowledge of model diagnostics procedures available for checking crucial assumptions, and, finally, an under- standing of the limitations in the validity of the underlying hypotheses of the fitted model and its implication for the precision of parameter estimates. Current nonlinear regression modules lack dedicated diagnostic functionality. So there is a need to provide users with an extended toolbox of functions enabling a careful evaluation of nonlinear regression fits. To this end, we introduce a unified diagnostic framework with the R package nlstools.
    [Show full text]
  • Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver
    Information • Textbooks • Media • Resources edited by Computer Bulletin Board Steven D. Gammon University of Idaho Moscow, ID 83844 Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver Daniel C. Harris Chemistry & Materials Branch, Research & Technology Division, Naval Air Warfare Center,China Lake, CA 93555 A powerful tool that is widely available in spreadsheets Unweighted Least Squares provides a simple means of fitting experimental data to non- linear functions. The procedure is so easy to use and its Experimental values of x and y from Figure 1 are listed mode of operation is so obvious that it is an excellent way in the first two columns of the spreadsheet in Figure 2. The for students to learn the underlying principle of least- vertical deviation of the ith point from the smooth curve is squares curve fitting. The purpose of this article is to intro- vertical deviation = yi (observed) – yi (calculated) (2) duce the method of Walsh and Diamond (1) to readers of = yi – (Axi + B/xi + C) this Journal, to extend their treatment to weighted least The least squares criterion is to find values of A, B, and squares, and to add a simple method for estimating uncer- C in eq 1 that minimize the sum of the squares of the verti- tainties in the least-square parameters. Other recipes for cal deviations of the points from the curve: curve fitting have been presented in numerous previous papers (2–16). n 2 Σ Consider the problem of fitting the experimental gas sum = yi ± Axi + B / xi + C (3) chromatography data (17) in Figure 1 with the van Deemter i =1 equation: where n is the total number of points (= 13 in Fig.
    [Show full text]
  • Archives of Agriculture and Environmental Science
    ISSN (Online) : 2456-6632 Archives of Agriculture and Environmental Science An International Journal Volume 4 | Issue 2 Agriculture and Environmental Science Academy www.aesacademy.org Scan to view it on the web Archives of Agriculture and Environmental Science (Abbreviation: Arch. Agr. Environ. Sci.) ISSN: 2456-6632 (Online) An International Research Journal of Agriculture and Environmental Sciences Volume 4 Number 2 2019 Abstracted/Indexed: The journal AAES is proud to be a registered member of the following leading abstracting/indexing agencies: Google Scholar, AGRIS-FAO, CrossRef, Informatics, jGate @ e-Shodh Sindhu, WorldCat Library, OpenAIRE, Zenodo ResearchShare, DataCite, Index Copernicus International, Root Indexing, Research Gate etc. All Rights Reserved © 2016-2019 Agriculture and Environmental Science Academy Disclaimer: No part of this booklet may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without written permission of the publisher. However, all the articles published in this issue are open access articles which are distributed under the terms of the Creative Commons Attribution 4.0 License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited For information regarding permission, write us [email protected]. An official publication of Agriculture and Environmental Science Academy 86, Gurubaksh Vihar (East) Kankhal Haridwar-249408 (Uttarakhand), India Website: https://www.aesacademy.org Email: [email protected] Phone: +91-98971-89197 Archives of Agriculture and Environmental Science (An International Research Journal) (Abbreviation: Arch. Agri. Environ. Sci.) Aims & Objectives: The journal is an official publication of Agriculture and Environmental Science Academy.
    [Show full text]
  • An Efficient Nonlinear Regression Approach for Genome-Wide
    An Efficient Nonlinear Regression Approach for Genome-wide Detection of Marginal and Interacting Genetic Variations Seunghak Lee1, Aur´elieLozano2, Prabhanjan Kambadur3, and Eric P. Xing1;? 1School of Computer Science, Carnegie Mellon University, USA 2IBM T. J. Watson Research Center, USA 3Bloomberg L.P., USA [email protected] Abstract. Genome-wide association studies have revealed individual genetic variants associated with phenotypic traits such as disease risk and gene expressions. However, detecting pairwise in- teraction effects of genetic variants on traits still remains a challenge due to a large number of combinations of variants (∼ 1011 SNP pairs in the human genome), and relatively small sample sizes (typically < 104). Despite recent breakthroughs in detecting interaction effects, there are still several open problems, including: (1) how to quickly process a large number of SNP pairs, (2) how to distinguish between true signals and SNPs/SNP pairs merely correlated with true sig- nals, (3) how to detect non-linear associations between SNP pairs and traits given small sam- ple sizes, and (4) how to control false positives? In this paper, we present a unified framework, called SPHINX, which addresses the aforementioned challenges. We first propose a piecewise linear model for interaction detection because it is simple enough to estimate model parameters given small sample sizes but complex enough to capture non-linear interaction effects. Then, based on the piecewise linear model, we introduce randomized group lasso under stability selection, and a screening algorithm to address the statistical and computational challenges mentioned above. In our experiments, we first demonstrate that SPHINX achieves better power than existing methods for interaction detection under false positive control.
    [Show full text]
  • Strategies for Non-Invasive Management of High-Grade Cervical Intraepithelial Neoplasia
    Strategies for non-invasive management of high-grade cervical intraepithelial neoplasia Citation for published version (APA): Koeneman, M. M. (2019). Strategies for non-invasive management of high-grade cervical intraepithelial neoplasia: prognostic biomarkers and immunotherapy. Maastricht University. https://doi.org/10.26481/dis.20190116mk Document status and date: Published: 01/01/2019 DOI: 10.26481/dis.20190116mk Document Version: Publisher's PDF, also known as Version of record Please check the document version of this publication: • A submitted manuscript is the version of the article upon submission and before peer-review. There can be important differences between the submitted version and the official published version of record. People interested in the research are advised to contact the author for the final version of the publication, or visit the DOI to the publisher's website. • The final author version and the galley proof are versions of the publication after peer review. • The final published version features the final layout of the paper including the volume, issue and page numbers. Link to publication General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal.
    [Show full text]
  • (EU FP7 2013 - 612218/3D-NET) 3DNET Sops HOW-TO-DO PRACTICAL GUIDE
    3D-NET (EU FP7 2013 - 612218/3D-NET) 3DNET SOPs HOW-TO-DO PRACTICAL GUIDE Curve fitting This is intended to be an aid-memoir for those involved in fitting biological data to dose response curves in why we do it and how to best do it. So why do we use non linear regression? Much of the data generated in Biology is sigmoidal dose response (E/[A]) curves, the aim is to generate estimates of upper and lower asymptotes, A50 and slope parameters and their associated confidence limits. How can we analyse E/[A] data? Why fit curves? What’s wrong with joining the dots? Fitting Uses all the data points to estimate each parameter Tell us the confidence that we can have in each parameter estimate Estimates a slope parameter Fitting curves to data is model fitting. The general equation for a sigmoidal dose-response curve is commonly referred to as the ‘Hill equation’ or the ‘four-parameter logistic equation”. (Top Bottom) Re sponse Bottom EC50hillslope 1 [Drug]hillslpoe The models most commonly used in Biology for fitting these data are ‘model 205 – Dose response one site -4 Parameter Logistic Model or Sigmoidal Dose-Response Model’ in XLfit (package used in ActivityBase or Excel) and ‘non-linear regression - sigmoidal variable slope’ in GraphPad Prism. What the computer does - Non-linear least squares Starts with an initial estimated value for each variable in the equation Generates the curve defined by these values Calculates the sum of squares Adjusts the variables to make the curve come closer to the data points (Marquardt method) Re-calculates the sum of squares Continues this iteration until there’s virtually no difference between successive fittings.
    [Show full text]
  • A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen
    Current Chemical Genomics, 2010, 4, 57-66 57 Open Access A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen National Institutes of Health, NIH Chemical Genomics Center, 9800 Medical Center Drive, Rockville, MD 20850, USA Abstract: We describe a novel algorithm, Grid algorithm, and the corresponding computer program for high throughput fitting of dose-response curves that are described by the four-parameter symmetric logistic dose-response model. The Grid algorithm searches through all points in a grid of four dimensions (parameters) and finds the optimum one that corre- sponds to the best fit. Using simulated dose-response curves, we examined the Grid program’s performance in reproduc- ing the actual values that were used to generate the simulated data and compared it with the DRC package for the lan- guage and environment R and the XLfit add-in for Microsoft Excel. The Grid program was robust and consistently recov- ered the actual values for both complete and partial curves with or without noise. Both DRC and XLfit performed well on data without noise, but they were sensitive to and their performance degraded rapidly with increasing noise. The Grid program is automated and scalable to millions of dose-response curves, and it is able to process 100,000 dose-response curves from high throughput screening experiment per CPU hour. The Grid program has the potential of greatly increas- ing the productivity of large-scale dose-response data analysis and early drug discovery processes, and it is also applicable to many other curve fitting problems in chemical, biological, and medical sciences.
    [Show full text]
  • Model Selection, Transformations and Variance Estimation in Nonlinear Regression
    Model Selection, Transformations and Variance Estimation in Nonlinear Regression Olaf Bunke1, Bernd Droge1 and J¨org Polzehl2 1 Institut f¨ur Mathematik, Humboldt-Universit¨at zu Berlin PSF 1297, D-10099 Berlin, Germany 2 Konrad-Zuse-Zentrum f¨ur Informationstechnik Heilbronner Str. 10, D-10711 Berlin, Germany Abstract The results of analyzing experimental data using a parametric model may heavily depend on the chosen model. In this paper we propose procedures for the ade- quate selection of nonlinear regression models if the intended use of the model is among the following: 1. prediction of future values of the response variable, 2. estimation of the un- known regression function, 3. calibration or 4. estimation of some parameter with a certain meaning in the corresponding field of application. Moreover, we propose procedures for variance modelling and for selecting an appropriate nonlinear trans- formation of the observations which may lead to an improved accuracy. We show how to assess the accuracy of the parameter estimators by a ”moment oriented bootstrap procedure”. This procedure may also be used for the construction of confidence, prediction and calibration intervals. Programs written in Splus which realize our strategy for nonlinear regression modelling and parameter estimation are described as well. The performance of the selected model is discussed, and the behaviour of the procedures is illustrated by examples. Key words: Nonlinear regression, model selection, bootstrap, cross-validation, variable transformation, variance modelling, calibration, mean squared error for prediction, computing in nonlinear regression. AMS 1991 subject classifications: 62J99, 62J02, 62P10. 1 1 Selection of regression models 1.1 Preliminary discussion In many papers and books it is discussed how to analyse experimental data estimating the parameters in a linear or nonlinear regression model, see e.g.
    [Show full text]