Arrêté N° 2014161-0009 Du 10 Juin 2014 Objet
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Feuille1 Page 1 Agen-D'aveyron 8 €/M² Aguessac 8 €/M² Les Albres 8
Feuille1 Agen-d'Aveyron 8 €/m² Aguessac 8 €/m² Les Albres 8 €/m² Almont-les-Junies 8 €/m² Alpuech 8 €/m² Alrance 8 €/m² Ambeyrac 8 €/m² Anglars-Saint-Félix 8 €/m² Arnac-sur-Dourdou 8 €/m² Arques 8 €/m² Arvieu 8 €/m² Asprières 8 €/m² Aubin 8 €/m² Aurelle-Verlac 8 €/m² Auriac-Lagast 8 €/m² Auzits 8 €/m² Ayssènes 8 €/m² Balaguier-d'Olt 8 €/m² Balaguier-sur-Rance 8 €/m² Balsac 8 €/m² La Bastide-l'Évêque 8 €/m² La Bastide-Pradines 8 €/m² La Bastide-Solages 8 €/m² Belcastel 8 €/m² Belmont-sur-Rance 8 €/m² Bertholène 8 €/m² Bessuéjouls 8 €/m² Boisse-Penchot 8 €/m² Bor-et-Bar 8 €/m² Bouillac 8 €/m² Bournazel 8 €/m² Boussac 8 €/m² Bozouls 8 €/m² Brandonnet 8 €/m² Brasc 8 €/m² Brommat 8 €/m² Broquiès 8 €/m² Brousse-le-Château 8 €/m² Brusque 8 €/m² Buzeins 8 €/m² Cabanès 8 €/m² Calmels-et-le-Viala 8 €/m² Calmont 8 €/m² Camarès 8 €/m² Camboulazet 8 €/m² Camjac 8 €/m² Page 1 Feuille1 Campagnac 8 €/m² Campouriez 8 €/m² Campuac 8 €/m² Canet-de-Salars 8 €/m² Cantoin 8 €/m² Capdenac-Gare 8 €/m² La Capelle-Balaguier 8 €/m² La Capelle-Bleys 8 €/m² La Capelle-Bonance 8 €/m² Baraqueville 8 €/m² Cassagnes-Bégonhès 8 €/m² Cassuéjouls 8 €/m² Castanet 8 €/m² Castelmary 8 €/m² Castelnau-de-Mandailles 8 €/m² Castelnau-Pégayrols 8 €/m² La Cavalerie 8 €/m² Le Cayrol 8 €/m² Centrès 8 €/m² Clairvaux-d'Aveyron 8 €/m² Le Clapier 8 €/m² Colombiès 8 €/m² Combret 8 €/m² Compeyre 8 €/m² Compolibat 8 €/m² Comprégnac 8 €/m² Comps-la-Grand-Ville 8 €/m² Condom-d'Aubrac 8 €/m² Connac 8 €/m² Conques 8 €/m² Cornus 8 €/m² Les Costes-Gozon 8 €/m² Coubisou 8 €/m² Coupiac 8 €/m² Coussergues -

Musées Et Espaces Scénographiques Patrimoine Museums & Rendering Areas Patrimony / Patrimonio
DESTINATION PAYS DECAZEVILLOIS - VALLÉE DU LOT GUIDE TOURISTIQUE 2020 DECAZEVILLE COMMUNAUTÉ www.tourisme-paysdecazevillois.fr Saint-San�n Sain aniol vers Aurillac Grand Vabre Saint Parthem P Agrès Flagnac Conques Almont-les-Junies Livinhac-le-haut Boisse- Penchot agax vers Figeac Bouillac Laroque Labessenoits Noailhac Decazeville Viviez Saint Cyprien sur Dourdou Firmi Combes VISIT'QUIZ vers Rodez - Marcillac Visitez notre territoire Aubin autrement ! Au détour d’une balade, d’une Cransac-les-Thermes randonnée, d’une visite sur notre vers Villefranche de Rouergue territoire, découvrez les richesses Montauban - Toulouse de notre patrimoine et participez vers Rignac Bournazel ainsi au Visit’Quiz et tentez de devenir le grand champion annuel ! Retirez votre livret dans l’un des 3 bureaux de l'Office de Tourisme Auzits et du Thermalisme de Decazeville Communauté. 3 grands gagnants ! En partenariat avec les Thermes de Cransac et les producteurs locaux. 2 Découvrez La destination Pays decazevillois - Vallée Saint-San�n Sain aniol du Lot est située à l’ouest du département de l’Aveyron, alliant les richesses du passé industriel et minier et les charmes de la vers Aurillac rivière Lot. Grand Vabre Carrefour des contrastes, notre région est Saint Parthem une invitation à la découverte, à la détente, P Agrès aux plaisirs de la table, à la convivialité, à l’authenticité. Flagnac Partez à la rencontre d’un territoire Conques atypique, changez de rythme, plongez Almont-les-Junies dans le bien-être, retrouvez l’histoire des Livinhac-le-haut hommes. Boisse- Penchot agax vers Figeac Bouillac Laroque To discover Labessenoits Our area is situated in the Western Aveyron combining the industrial and mining history with Noailhac the beauty of the Lot river. -

Décision De L'autorité Environnementale, Après Examen
Décision de l’Autorité environnementale, après examen au cas par cas, sur le plan de prévention des risques d’inondation de la moyenne et basse vallée de l’Aveyron (PPRI) n° : F- 076-19-P-0039 Décision n° F- 076-19-P-0039 en date du 31 mai 2019 Autorité environnementale Ae – Décision en date du 31 mai 2019 – Plan de prévention des risques d’inondation de la moyenne et basse vallée de l’Aveyron Décision du 31 mai 2019 après examen au cas par cas en application de l ’article R. 122 -17 du code de l ’environnement Le président de la formation d’autorité environnementale du Conseil général de l’environnement et du développement durable ; Vu la directive n°2001/42/CE du Parlement Européen et du Conseil du 27 juin 2001 relative à l’évaluation des incidences de certains plans et programmes sur l’environnement et notamment son annexe II ; Vu le code de l’environnement, notamment ses articles L. 122-4, L. 122-5, R. 122-17 et R. 12218 ; Vu le décret n° 2015-1229 du 2 octobre 2015 modifié relatif au Conseil général de l’environnement et du développement durable ; Vu l’arrêté de la ministre de l’environnement, de l’énergie et de la mer du 12 mai 2016 portant approbation du règlement intérieur du Conseil général de l’environnement et du développement durable ; Vu la décision prise par la formation d’autorité environnementale du Conseil général de l’environnement et du développement durable dans sa réunion du 31 mai 2017 portant exercice des délégations prévues à l’article 17 du décret n° 2015-1229 du 2 octobre 2015 modifié relatif au Conseil général de l’environnement et du développement durable ; Vu la demande d’examen au cas par cas (y compris ses annexes) enregistrée sous le numéro n° F- 076-19-P-0039, présentée par la direction départementale des territoires de l’Aveyron, l’ensemble des pièces constitutives du dossier ayant été reçues le 28 mars 2019, relative au plan de prévention des risques d’inondation (PPRI) de la moyenne et basse vallée de l’Aveyron. -
3B2 to Ps Tmp 1..94
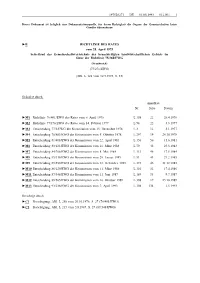
1975L0271 — DE — 01.05.1993 — 012.001 — 1 Dieses Dokument ist lediglich eine Dokumentationsquelle, für deren Richtigkeit die Organe der Gemeinschaften keine Gewähr übernehmen ►B RICHTLINIE DES RATES vom 28. April 1975 betreffend das Gemeinschaftsverzeichnis der benachteiligten landwirtschaftlichen Gebiete im Sinne der Richtlinie 75/268/EWG (Frankreich) (75/271/EWG) (ABl. L 128 vom 19.5.1975, S. 33) Geändert durch: Amtsblatt Nr. Seite Datum ►M1 Richtlinie 76/401/EWG des Rates vom 6. April 1976 L 108 22 26.4.1976 ►M2 Richtlinie 77/178/EWG des Rates vom 14. Februar 1977 L 58 22 3.3.1977 ►M3 Entscheidung 77/3/EWG der Kommission vom 13. Dezember 1976 L 3 12 5.1.1977 ►M4 Entscheidung 78/863/EWG der Kommission vom 9. Oktober 1978 L 297 19 24.10.1978 ►M5 Entscheidung 81/408/EWG der Kommission vom 22. April 1981 L 156 56 15.6.1981 ►M6 Entscheidung 83/121/EWG der Kommission vom 16. März 1983 L 79 42 25.3.1983 ►M7 Entscheidung 84/266/EWG der Kommission vom 8. Mai 1984 L 131 46 17.5.1984 ►M8 Entscheidung 85/138/EWG der Kommission vom 29. Januar 1985 L 51 43 21.2.1985 ►M9 Entscheidung 85/599/EWG der Kommission vom 12. Dezember 1985 L 373 46 31.12.1985 ►M10 Entscheidung 86/129/EWG der Kommission vom 11. März 1986 L 101 32 17.4.1986 ►M11 Entscheidung 87/348/EWG der Kommission vom 11. Juni 1987 L 189 35 9.7.1987 ►M12 Entscheidung 89/565/EWG der Kommission vom 16. -

Relais Assistant(E)S Maternel(E)S Du Pays Segali
RELAIS ASSISTANT(E)S MATERNEL(E)S DU PAYS SEGALI REGLEMENT INTERIEUR Ceignac Baraqueville RAM du Pays Ségali Siège social 244 rue de la vallée 12160 BARAQUEVILLE Secteur « Baraquevillois » Secteur « Naucellois » Calmont - Ste Juliette Cassagnes Bégonhès 06 43 86 45 19 06 15 80 67 60 [email protected] [email protected] - 1 - Préambule Le présent règlement a pour objectif de présenter le fonctionnement du Relais Assistant(e)s Maternel(le)s et définir quels sont les droits et devoirs des utilisateurs de ce service. Il a été validé par le Président de Pays Ségali Communauté et par les partenaires financiers (CAF, MSA) Ce règlement a été réalisé à la demande de la CAF et sera évalué et ajusté en fonction des besoins du service. I) Présentation du Relais Assistant(e)s Maternel(le)s (RAM) : Le Relais Assistant(e)s Maternel(le)s fonctionne conformément à la lettre circulaire du 26 juillet 2017 de la CNAF (LC n°2017 – 003) Le Relais Assistant(e)s Maternel(le)s est un service gratuit, mis à disposition de la population et financé par Pays Ségali Communauté, la CAF et la MSA. Il fonctionne en itinérance toute la semaine. Son utilisation n’est en aucun cas une obligation. 1. Territoire couvert Depuis le 1er janvier 2018 Pays Ségali Communauté est gestionnaire du RAM avec un territoire qui comprend 23 communes : Baraqueville Boussac Cabanès Calmont Camboulazet Camjac Cassagnes- Bégonhès Castanet Castelmary Centrès Colombiès Crespin Tauriac de Naucelle Manhac Meljac Moyrazès Naucelle Pradinas Sauveterre de St Just sur Sainte Juliette Quins Gramond Rouergue Viaur 2. -

Meljac Année 1930
Meljac Année 1930 Le 26 février 1930 à midi, mariage de Parayre Pierre Auguste âgé de 31 ans, cultivateur à Laubigues ou il est né le 13 novembre 1898. Fils de Parayre Joseph et de Bousquet marie, cultivateurs à Laubigues. Albinet Lucie Mélanie Candie sans profession âgée de 19 ans, domiciliée à Grascazes ou elle est née le 17 mars 1910. Fille d’Albinet Pierre et d’Albinet Candie, cultivateurs à Grascazes. Contrat de mariage passé le 14 février 1930, devant Maître Richard notaire à Lédergues. Témoins : Ginestet Pierre, instituteur à Meljac. Feral Marie, institutrice à Meljac. Le 31 mars 1930 à 9 heures du matin au Feraldseq, est décédé Albinet Pierre Justin , né le 29 juin 1867 au Feraldesq, veuf de Trouche Marie. Fils des défunts Albinet Jean et Pesquié Rosalie. Témoins : Albinet J.Baptiste âgé de 52 ans, cultivateur à Cabrol. Le 10 avril 1930 à 3 heures du matin au Mas-Ricard, est née Loubière Maria Léa. Fille de Loubière Lucien né le 9 mars 1898 au Mas-Ricard et de Cailhol Philippine née le 9 mars 1901 à Ginestet commune de Centrès. Témoins : Loubière Lucien, père du nouveau-né. Mariée le 27 avril 1951 à Meljac, avec Paulhe Justin Frédéric Honoré. Le 1 juin 1929 à 9 heures du soir à Soulages, est né Rousel Gaston Augustin Pierre. Fils de Roussel Pierre Augustin né le 28 mars 1905 à Rodez et de Beaujour Augustine Léoncie née le 9 septembre 1912, cultivateurs à Soulages. Témoins : Roussel Pierre Augustin, père du nouveau-né. Marié le 28 novembre 1953 à Barry-d’eslemerde (tarn et Garonne), avec Thomcis Raymonde Marthe Irène. -

Transports Scolaires
TRANSPORTS SCOLAIRES Rentrée 2020 (SOUS RESERVE CHANGEMENT) ELEVES DEMI PENSIONNAIRES (TRANSPORT JOURNALIER) RUBAN BLEU MATIN MERCREDI SOIR LUNDI MAR. MER. JEU. VEND. MIDI LUN. MAR. MER. VENDREDI PLACE COMMISSARIAT VILLEFRANCHE 9 H 00 7 H 30 12 H 00 17 H 50 16 H 15 MONTEILS 9 H 25 7 H 55 11 H 40 17 H 25 15 H 50 DIRECTIONS + CORRESPONDANCES TRANSPORTEURS TELEPHONES NAJAC, MARTIEL, VILLENEUVE, LACAPELLE-BALAGUIER, LANUEJOULS, MONTBAZENS RUBAN BLEU 05.65.81.12.92 RIEUPEYROUX CHAUCHARD 05.65.65.17.20 CAYLUS JARDEL 05.63.22.55.00 Services Conseil Général Aveyron 05.65.75.80.10 ELEVES PENSIONNAIRES (TRANSPORT HEBDOMADAIRE) RODEZ (GARE ROUTIERE) / LA PRIMAUBE / BARAQUEVILLE / RIEUPEYROUX / VILLEFRANCHE-DE-ROUERGUE / MONTEILS RODEZ LIGNE PRIVÉE LA PRIMAUBE BARAQUEVILLE RIEUPEYROUX VILLEFRANCHE MONTEILS CAR DU LYCEE F. MARTY GARE ROUTIERE LUNDI MATIN 7 H 55 8 H 10 8 H 25 8 H 45 9 H 00 9 H 25 VENDREDI SOIR 17 H 20 17 H 00 16 H 50 16 H 30 16 H 15 15 H 50 LES ELEVES DOIVENT ETRE PRESENTS, SUR LE LIEU DE RENDEZ-VOUS ET DE PRISE EN CHARGE, 5 MN AVANT L’HORAIRE MENTIONNE LIGNES REGIONALES ESPALION BOZOULS LIOUJAS SEBAZAC RODEZ LIGNE 201 LAGUIOLE PUIS CAR BD JOSEPH POULENC LA ROTONDE LA LOUBIERE LE TREMBLANT GARE ROUTIERE DU LYCEE LUNDI MATIN --- 6 H 45 7 H 00 7 H 10 7 H 15 7 H 25 RODEZ VENDREDI SOIR 18 H 45 18 H 10 17 H 50 17 H 47 17 H 40 17 H 30 MONTEILS VILLEFRANCHE LIGNE 205 FIGEAC CAUSSE ET DIEGE VILLENEUVE AVEYRON SAINT REMY PUIS CAR RUBAN PL.DE LA LIBERTE BLEU LYCEE LUNDI MATIN 7 H 45 8 H 00 8 H 14 8 H 20 8 H 30 VILLENFRANCHE VENDREDI SOIR 18 -

Généalogie Ascendante De Marie Joséphine VIGUIÉ (1858 - 1933)
Généalogie ascendante de Marie Joséphine VIGUIÉ (1858 - 1933) No Nom et prénoms, Profession, Date et lieu de naissance Date et lieu de Décès Sosa Date et lieu de Mariage Génération I 1 VIGUIÉ Marie Joséphine N : 18/07/1858 Saint-Salvadou (12), Coustaux D : 31/08/1933 Saint-Salvadou (12), Fournaguet Génération II VIGUIÉ Joseph 2 N : 11/03/1815 Saint-Salvadou (12), Coustaux D : 16/07/1868 Saint-Salvadou (12), Coustaux Cultivateur à Cousteaux M : 04/06/1850 Lunac (12), Cd2-4e024070-17285699 et 5799 3 PRADINES Marie Martine N : 19/05/1830 Lunac (12), Farmond D : 07/10/1900 Saint-Salvadou (12), Coustaux Génération III VIGUIÉ Jean Pierre 4 N : 02/05/1777 Saint-Salvadou (12), Coustaux D : 22/02/1854 Saint-Salvadou (12), Coustaux Cultivateur à Coustaux M : 22/11/1812 Saint-Salvadou (12), Cd1-4e047625-08122999 5 SEGONS (Marie) Madeleine N : 13/01/1795 Saint-Salvadou (12), Le Puech D : 24/04/1853 Saint-Salvadou (12), Cousteaux PRADINES Jean Antoine 6 N : 07/09/1795 Lunac (12), Farmond D : 25/11/1849 Lunac (12), Farmond Cultivateur à Farmond M : 16/11/1825 Lunac (12), Cd1-4e024046-17151799 7 PASCAL Marianne N : 14/08/1807 L'Hom Lunac (12), L'Hom D : 24/05/1846 Lunac (12), Farmond Génération IV VIGUIE Simon 8 N : 29/10/1739 Saint-Salvadou (12), Le Cassan D : 28/11/1822 Saint-Salvadou (12), Coustaux Propriétaire, Laboureur à Coustaux M : 27/02/1775 Saint-Salvadou (12), Cd1-4e047595-14220999 et 1099 9 SEGONS Antoinette N : 10/04/1754 Saint-Salvadou (12), Le Puech D : 06/08/1780 Saint-Salvadou (12), Coustaux SEGONS Pierre 10 N : 10/01/1748 Saint-Salvadou -

DES SERVICES POUR TOUS « Construisons Dès À Présent Un Lendemain Attractif »
LE MAGAZINE DU CONSEIL DÉPARTEMENTAL JANVIER / FÉVRIER 2016 N° 203 DES SERVICES POUR TOUS « Construisons dès à présent un lendemain attractif » Sommaire Flashez ce code pour consulter ou télécharger 3 L’AVEYRON DU PRÉSIDENT la version en ligne. 4 L’AVEYRON EN ACTIONS .......Un laboratoire routier 6 L’AVEYRON SOLIDAIRE ..........Demain s’imagine aujourd’hui 8 L’AVEYRON D’ICI ...................Céor-Ségala et Enne & Alzou L’Aveyron 10 L’AVEYRON À DÉCOUVRIR ....Séverac d’Aveyron magazine édité par le Conseil départemental de l’Aveyron 12 L’AVEYRON DYNAMIQUE .......MJ2T vise surtout l’export Hôtel du Département BP 724 - 12007 RODEZ Cedex L’AVEYRON DE DEMAIN 13 .........Mélie Cauhapé Tél. 05 65 75 80 70 14 L’AVEYRON SPORTIF ..............Le FAR prépare l’emploi des jeunes www.aveyron.fr • N° I.S.S.N.1156-5527 16 L’AVEYRON CULTUREL ...........Une nouvelle dynamique • Directeur de publication : Jean-Claude Luche • Maquette / impression : Groupe Burlat Rodez 19 L’AVEYRON POLITIQUE ..........Expression des groupes politiques • Rédaction : L. Hortes • Photos : J.L. Bories - Agence CoCo Architecture L’AVEYRON D’ANTAN 20 .............Doménica la sulfureuse • Dépôt légal : 1er trimestre 2001 • Diffusion : 137 000 ex. Dans le souci du respect de l’environnement, ce document a été imprimé sur papier recyclé par une entreprise Imprim’Vert. Photo de couverture : Le centre Bourg de Bozoul LES SERVICES DU CONSEIL DÉPARTEMENTAL Adeca MDPH Enfance Seniors Info route Transports en danger scolaires Parce que le cancer Parce que le handicap Parce que l’enfance -

Cheeses Part 2
Ref. Ares(2013)3642812 - 05/12/2013 VI/1551/95T Rev. 1 (PMON\EN\0054,wpd\l) Regulation (EEC) No 2081/92 APPLICATION FOR REGISTRATION: Art. 5 ( ) Art. 17 (X) PDO(X) PGI ( ) National application No 1. Responsible department in the Member State: I.N.D.O. - FOOD POLICY DIRECTORATE - FOOD SECRETARIAT OF THE MINISTRY OF AGRICULTURE, FISHERIES AND FOOD Address/ Dulcinea, 4, 28020 Madrid, Spain Tel. 347.19.67 Fax. 534.76.98 2. Applicant group: (a) Name: Consejo Regulador de la D.O. "IDIAZÁBAL" [Designation of Origin Regulating Body] (b) Address: Granja Modelo Arkaute - Apartado 46 - 01192 Arkaute (Álava), Spain (c) Composition: producer/processor ( X ) other ( ) 3. Name of product: "Queso Idiazábaľ [Idiazábal Cheese] 4. Type of product: (see list) Cheese - Class 1.3 5. Specification: (summary of Article 4) (a) Name: (see 3) "Idiazábal" Designation of Origin (b) Description: Full-fat, matured cheese, cured to half-cured; cylindrical with noticeably flat faces; hard rind and compact paste; weight 1-3 kg. (c) Geographical area: The production and processing areas consist of the Autonomous Community of the Basque Country and part of the Autonomous Community of Navarre. (d) Evidence: Milk with the characteristics described in Articles 5 and 6 from farms registered with the Regulating Body and situated in the production area; the raw material,processing and production are carried out in registered factories under Regulating Body control; the product goes on the market certified and guaranteed by the Regulating Body. (e) Method of production: Milk from "Lacha" and "Carranzana" ewes. Coagulation with rennet at a temperature of 28-32 °C; brine or dry salting; matured for at least 60 days. -

Twinning in Pyromorphite: the First Documented Occurrence of Twinning by Merohedry in the Apatite Supergroup
American Mineralogist, Volume 97, pages 415–418, 2012 Twinning in pyromorphite: The first documented occurrence of twinning by merohedry in the apatite supergroup STUART J. MILLS,1,2,* GIOVANNI FERRARIS,3 ANTHONY R. KAMPF,2 AND GEORGES FAVREAU4 1Geosciences, Museum Victoria, GPO Box 666, Melbourne 3001, Australia 2Mineral Sciences Department, Natural History Museum of Los Angeles County, 900 Exposition Boulevard, Los Angeles, California 90007, U.S.A. 3Dipartimento di Scienze Mineralogiche e Petrologiche, Università degli Studi di Torino, Via Valperga Caluso 35, I-10125 Torino, Italy 4421 Avenue Jean Monnet, 13090 Aix-en-Provence, France ABSTRACT We describe the first documented case of {1010} twinning by reflection (or by twofold rotation about [100]) or merohedry (class II) in a member of the apatite supergroup. Twinning about [100] had previously been noted for the apatite supergroup but not confirmed. Pyromorphite crystals from Puech de Compolibat, Combret, Aveyron, France, were studied by single-crystal X-ray diffraction 3 [a = 10.0017(19), c = 7.3413(16) Å, and V = 636.0(2) Å , in P63/m], where twinning was confirmed with the approximate twin fraction 62:38. Subsequent inspection of the morphology confirmed the nature of the twinning. The pyromorphite crystals are typically elongate and show the faces: (21 10), (2110), (0001), (0001), (1010), (1010), (101 2), and (1012). Keywords: Twinning by merohedry class II, pyromorphite, Puech de Compolibat, apatite supergroup, crystal structure INTRODUCTION and the center of symmetry 1 may always be considered as twin Twinning is the oriented association of two or more law. In class II twins, instead, the superimposed lattice nodes individuals that are related by a twin operation belonging to (and the corresponding superimposed diffracted intensities) are the point group either of the lattice (twinning by merohedry) not equivalent in the Laue group [e.g., crystal point group 6/m, or of a sublattice (twinning by reticular merohedry), but not Laue group 6/m, twin operation (1010) plane]. -

Plan De Prevention Des Risques D'inondation
PREFET DE L'AVEYRON Direction Départementale PP PP RR II des Territoires Service Énergie, Risques, Bâtiment et Sécurité Unité PLAN DE PREVENTION Prévention des Risques DES RISQUES D'INONDATION CEOR GIFFOU 1 – NOTE DE PRESENTATION Prescrit par arrêté préfectoral du 28 mai 2015 Approuvé par arrêté préfectoral Décembre du DOSSIER D'APPROBATION 2015 PPRI du Céor-Giffou : rapport de présentation Mars 2015 - SOMMAIRE - I. PREAMBULE...................................................................................................................... 3 1.1. Cadre de l’étude............................................................................................... 3 1.2. Objet de l’étude ............................................................................................... 4 1.3. Déroulement de l’étude .................................................................................. 5 II. Démarche d’étude .............................................................................................................. 6 2.1. Diagnostic hydrogéomorphologique préalable ............................................... 6 2.2. Évaluation des critère d’aléas.......................................................................... 9 2.3. Évaluation des enjeux.................................................................................... 12 III. Présentation du secteur d’étude .................................................................................... 21 3.1. Présentation géographique du bassin-versant du Céor-Giffou....................