DOCSLIB.ORG

Bernoulli-Gaussian Distribution with Memory As a Model for Power Line Communication Noise Victor Fernandes, Weiler A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bernoulli-Gaussian Distribution with Memory As a Model for Power Line Communication Noise Victor Fernandes, Weiler A XXXV SIMPOSIO´ BRASILEIRO DE TELECOMUNICAC¸ OES˜ E PROCESSAMENTO DE SINAIS - SBrT2017, 3-6 DE SETEMBRO DE 2017, SAO˜ PEDRO, SP Bernoulli-Gaussian Distribution with Memory as a Model for Power Line Communication Noise Victor Fernandes, Weiler A. Finamore, Mois´es V. Ribeiro, Ninoslav Marina, and Jovan Karamachoski Abstract— The adoption of Additive Bernoulli-Gaussian Noise very useful to come up with a as simple as possible models (ABGN) as an additive noise model for Power Line Commu- of PLC noise, similar to the additive white Gaussian noise nication (PLC) systems is the subject of this paper. ABGN is a (AWGN) model. model that for a fraction of time is a low power noise and for the remaining time is a high power (impulsive) noise. In this context, In this regard, we introduce the definition of a simple and we investigate the usefulness of the ABGN as a model for the useful mathematical model for the noise perturbing the data additive noise in PLC systems, using samples of noise registered transmission over PLC channel that would be a helpful tool. during a measurement campaign. A general procedure to find the With this goal in mind, an investigation of the usefulness of model parameters, namely, the noise power and the impulsiveness what we call additive Bernoulli-Gaussian noise (ABGN) as a factor is presented. A strategy to assess the noise memory, using LDPC codes, is also examined and we came to the conclusion that model for the noise perturbing the digital communication over ABGN with memory is a consistent model that can be used as for PLC channel is discussed. The ABGN is a discrete-time and the evaluation of the noise effect on the digital communication memoryless model that is equivalent to the continuous-time over PLC channel even when the PLC system uses the memory- Two-state, Middleton Class A model. Moreover, a comparison dependent (i.e. error control codes) consistency that do not hold performance analysis of the digital communication system when using the (memoryless) ABGN model. when the transmission is perturbed by the measured noise and Keywords— power line communication, power line noise model, by the noise generated according to ABGN model is discussed. Bernoulli-Gaussian noise, noise with memory, impulsive noise Due to the limitation of ABGN model to handle memory- sensitive procedures, we propose a more sophisticated model, I. INTRODUCTION which takes into account the memory that is intrinsic to the The Power Line Communication (PLC) channel is perturbed nature of the PLC noise. This model is so-called ABGN with by noise which is commonly considered to be a stochastic memory (ABGNM) and it is suitable for PLC systems that process. For a given percentage of the time it is in an impulsive make use of any memory-dependent tool (e.g., error control state (high or “strong” noise power) and for the remaining time codes). is on the background state (low or “weak” noise power). The Basedonthepresentedanalyses,wecameuptothe characterization of the noise perturbing PLC channel (hereafter conclusion that the ABGN model is a good model for the called PLC noise) has been the subject of studies and some PLC noise when the digital communication system does not models have been proposed in order to mimic the measured use any memory-sensitive procedure. However, it does not PLC noise behavior without the need to realize a measure mimic the system performance with measured noise when it campaign [1]–[3]. A widely accepted model is the Middleton has memory, which is a similar behavior of Middleton Class A Class A, which assumes that the noise impulsiveness level is model. Finally, we show that the ABGNM model can mimic classified in an infinite number of states [4]. As shown in [5], the measured PLC noise, resulting in a similar performance the Two-state, Middleton Class A model can be as good as the for both measured and synthetic noises even when the digital general Middleton Class A, agreeing with the fact that a two- communication system has any memory-dependent tool (e.g., state model offers a good balancing between the usefulness error control codes). and simplicity. By reviewing the literature, we note that the Middleton II. COMMUNICATION SYSTEM MODEL Class A model was not evaluated when memory-dependent A digital communication system in which a modulated tool is taken into account. This is an important issue because signal is transmitted through a medium is, in its simplest the noise model must be able to capture the behavior of PLC form, modeled by a channel, where the input signal at the noise when error control code is used. Moreover, it would be receiver is y(t)=s(t)+w(t). This corresponds to modeling a transmission medium by the channel in which s(t) is the Victor Fernandes is with Universidade Federal de Juiz de Fora (UFJF), Juiz channel input (modulated signal), w(t) represents the noise de Fora - MG, Brazil. E-mail: [email protected]. Weiler A. Finamore is with Universidade Federal de Juiz de Fora (UFJF), perturbing the transmission, and y(t) is the channel output. In Juiz de Fora - MG, Brazil and University of Information Sciences and Tech- this section, we focus on a digital communication system with nology (UIST), Ohrid, Republic of Macedonia. E-mail: fi[email protected]. a binary phase shift keying (BPSK) modulator, transmitting a Mois´es V. Ribeiro is with Universidade FederaldeJuizdeFora(UFJF), th Juiz de Fora - MG, Brazil and Smarti9 Ltda. E-mail: [email protected]. string of bits, which its i bit is represented by {ui} (i ∈ Z Ninoslav Marina and Jovan Karamachoski are with University of Infor- and ui ∈{0, 1}). The modulated signal is expressed by mation Sciences and Technology (UIST), Ohrid, Republic of Macedonia. E- ∞ mails: [email protected], [email protected]. This work was partially supported by CNPq, CAPES, FAPEMIG, FINEP, s(t)= (1 − 2ui)p(t − iT )cos2πfct, (1) INERGE, and Smarti9 Ltda. i=−∞ 328 XXXV SIMPOSIO´ BRASILEIRO DE TELECOMUNICAC¸ OES˜ E PROCESSAMENTO DE SINAIS - SBrT2017, 3-6 DE SETEMBRO DE 2017, SAO˜ PEDRO, SP in which the formatting pulse is p(t) with energy equal to one, B. Bernoulli-Gaussian Noise T f is the signaling interval, and c is the modulating frequency. The ABGN is a discrete-time and memoryless model that is equivalent to the continuous-time Two-state Middleton Class A A. White Gaussian Noise model. In this model, besides the background noise power, characterized by N0, two other parameters: α (which char- y t s t w t The channel output (receiver input) ( )= ( )+ ( ), acterizes how much stronger than the background noise the representing the input signal added to the noise, is the ob- impulsive noise is) and p (which characterizes the percentage servation that will be used by the receiver to estimate the of time that only background noise is present) are used when information that has been sent. The noise perturbing the digital specifying the ABGN(N0,p,α) model. communication is, in many situations, modeled as a zero A digital communication system in which a modulated W t mean stochastic process ( ) with power spectral density signal is transmitted over a PLC channel is, in its simplest SW (f)=N0/2, rendering a value (at the decider input) s t 2 2 form, modeled as having the signal ( ), at the channel input σ = N0/2 σ with variance 0 . This is the simple AWGN( 0) and yPLC(t)=s(t)+wPLC(t) is the channel output, where model which have been extensively used to model different wPLC(t) is the PLC additive noise. E communication channels. The energy-per-bit b at the receiver As discussed in [7], the received and filtered PLC noise E /N input and the ratio b 0, of the energy-per-bit and the noise can be modeled as a stochastic process V (t). At the receiver parameter (a parameter of interest to characterize the state of end (at the input of the decider), at a given time instant t1, the system), can be easily calculated from (1). V (t1) can be a zero mean “weak” Gaussian rv with variance In such digital communication systems, assuming perfect 2 σ0 and, at a distinct time instant t2, V (t2) can be a zero mean synchronization, the continuous signal y(t) is processed by 2 2 2 “strong” Gaussian rv with variance σ1 = α σ0 ,(α>1). the receiver as follows: V (t1) and V (t2) are independent rvs. The noise component {V } σ2,p,α yo(t)=y(t)2 cos 2πfct sequence n , which can be modeled as an ABGN( 0 ), is defined as follows [8]: r(t)=yo(t) ∗ p(T − t) r(t)=([s(t)+w(t)]2 cos 2πfct) ∗ p(T − t) 2 th Definition #1 (ABGN(σ ,p,α)): Let {Un} be the n ∞ 0 sample of a sequence of Bernoulli rv with P[Un =1]=p r(t)= (1 − 2ui)q(t − iT )+2w(t)cos2πfct ∗ p(T − t) i=−∞ (and, of course, P[Un =0]=1− p)and{Wn} be a sequence σ2 rn = r(t)|t=nT of i.i.d. Gaussian rv with zero mean and variance 0 .The th ∞ sequence of rvs, {Vn}, with the n sample given by = (1 − 2un)δn−i + wn. (2) Vn = UnWn + α(1 − Un)Wn, (4) i=−∞ ∗ p(t) ∗ p(−t)=q(t) 2 where denotes linear convolution, in which α>1, is an ABGN(σ0,p,α). fulfill the 1st criterion of Nyquist for having free intersymbol δ w nth interference, n is the impulse sequence, and n is the Every sample Vn = αWn corresponding to Un =0,is z − u w discrete-time noise sample.
Load more

Recommended publications
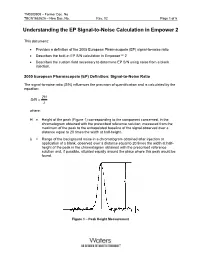
  • EP Signal to Noise in Emp 2
    TN0000909 – Former Doc. No. TECN1852625 – New Doc. No. Rev. 02 Page 1 of 5 Understanding the EP Signal-to-Noise Calculation in Empower 2 This document: • Provides a definition of the 2005 European Pharmacopeia (EP) signal-to-noise ratio • Describes the built-in EP S/N calculation in Empower™ 2 • Describes the custom field necessary to determine EP S/N using noise from a blank injection. 2005 European Pharmacopeia (EP) Definition: Signal-to-Noise Ratio The signal-to-noise ratio (S/N) influences the precision of quantification and is calculated by the equation: 2H S/N = λ where: H = Height of the peak (Figure 1) corresponding to the component concerned, in the chromatogram obtained with the prescribed reference solution, measured from the maximum of the peak to the extrapolated baseline of the signal observed over a distance equal to 20 times the width at half-height. λ = Range of the background noise in a chromatogram obtained after injection or application of a blank, observed over a distance equal to 20 times the width at half- height of the peak in the chromatogram obtained with the prescribed reference solution and, if possible, situated equally around the place where this peak would be found. Figure 1 – Peak Height Measurement TN0000909 – Former Doc. No. TECN1852625 – New Doc. No. Rev. 02 Page 2 of 5 In Empower 2 software, the EP Signal-to-Noise (EP S/N) is determined in an automated fashion and does not require a blank injection. The intention of this calculation is to preserve the sense of the EP calculation without requiring a separate blank injection.
    [Show full text]
  • Measurement and Estimation of the Mode Partition Coefficient K
    Measurement and Estimation of the Mode Partition Coefficient k Rick Pimpinella and Jose Castro IEEE P802.3bm 40 Gb/s and 100 Gb/s Fiber Optic Task Force November 2012, San Antonio, TX Background & Objective Background: Mode Partition Noise in MMF channel links is caused by pulse-to-pulse power fluctuations among VCSEL modes and differential delay due to dispersion in the fiber (Power independent penalty) “k” is an index used to describe the degree of mode fluctuations and takes on a value between 0 and 1, called the mode partition coefficient [1,2] Currently the IEEE link model assumes k = 0.3 It has been discussed that a new link model requires validation of k The measurement & estimation of k is challenging due to several conditions: Low sensitivity of detectors at 850nm The presence of additional noise components in VCSEL-MMF channels (RIN, MN, Jitter – intensity fluctuations, reflection noise, thermal noise, …) Differences in VCSEL designs Objective: Provide an experimental estimate of the value of k for VCSELs Additional work in progress 2 MPN Theory Originally derived for Fabry-Perot lasers and SMF [3] Assumptions: Total power of all modes carried by each pulse is constant Power fluctuations among modes are anti-correlated Mechanism: When modes (different wavelengths) travel at the same speed their fluctuations remain anti-correlated and the resultant pulse-to-pulse noise is zero. When modes travel in a dispersive medium the modes undergo different delays resulting in pulse distortions and a noise penalty. Example: Two VCSEL modes transmitted in a SMF undergoing chromatic dispersion: START END Optical Waveform @ Detector START t END With mode power fluctuations Decision Region Shorter Wavelength Time (arrival) t slope DL Time (arrival) Longer Wavelength Time (arrival) 3 Example of Intensity Fluctuation among VCSEL modes MPN can be observed using an Optical Spectrum Analyzer (OSA).
    [Show full text]
  • Introduction to Noise Measurements on Business Machines (Bo0125)
    BO 0125-11 Introduction to Noise Measurements on Business Machines by Roger Upton, B.Sc. Introduction In recent years, manufacturers of DIN 45 635 pt.19 ization committees in the pursuit of business machines, that is computing ANSI Si.29, (soon to be superced- harmonization, meaning that the stan- and office machines, have come under ed by ANSI S12.10) dards agree with each other in the increasing pressure to provide noise ECMA 74 bulk of their requirements. This appli- data on their products. For instance, it ISO/DIS 7779 cation note first discusses some acous- is becoming increasingly common to tic measurement parameters, and then see noise levels advertised, particular- With four separate standards in ex- the measurements required by the ly for printers. A number of standards istence, one might expect some con- various standards. Finally, it describes have been written governing how such siderable divergence in their require- some Briiel & Kjaer measurement sys- noise measurements should be made, ments. However, there has been close terns capable of making the required namely: contact between the various standard- measurements. Introduction to Noise Measurement Parameters The standards referred to in the previous section call for measure• ments of sound power and sound pres• sure. These measurements can then be used in a variety of ways, such as noise labelling, prediction of installation noise levels, comparison of noise emis• sions of products, and production con• trol. Sound power and sound pressure are fundamentally different quanti• ties. Sound power is a measure of the ability of a device to make noise. It is independent of the acoustic environ• ment.
    [Show full text]
  • Background Noise, Noise Sensitivity, and Attitudes Towards Neighbours, and a Subjective Experiment Using a Rubber Ball Impact Sound
    International Journal of Environmental Research and Public Health Article Background Noise, Noise Sensitivity, and Attitudes towards Neighbours, and a Subjective Experiment Using a Rubber Ball Impact Sound Jeongho Jeong Fire Insurers Laboratories of Korea, 1030 Gyeongchungdae-ro, Yeoju-si 12661, Korea; [email protected]; Tel.: +82-31-887-6737 Abstract: When children run and jump or adults walk indoors, the impact sounds conveyed to neighbouring households have relatively high energy in low-frequency bands. The experience of and response to low-frequency floor impact sounds can differ depending on factors such as the duration of exposure, the listener’s noise sensitivity, and the level of background noise in housing complexes. In order to study responses to actual floor impact sounds, it is necessary to investigate how the response is affected by changes in the background noise and differences in the response when focusing on other tasks. In this study, the author presented subjects with a rubber ball impact sound recorded from different apartment buildings and housings and investigated the subjects’ responses to varying levels of background noise and when they were assigned tasks to change their level of attention on the presented sound. The subjects’ noise sensitivity and response to their neighbours were also compared. The results of the subjective experiment showed differences in the subjective responses depending on the level of background noise, and high intensity rubber ball impact sounds were associated with larger subjective responses. In addition, when subjects were performing a Citation: Jeong, J. Background Noise, task like browsing the internet, they attended less to the rubber ball impact sound, showing a less Noise Sensitivity, and Attitudes towards Neighbours, and a Subjective sensitive response to the same intensity of impact sound.
    [Show full text]
  • The Effects of Background Noise on Distortion Product Otoacoustic Emissions and Hearing Screenings Amy E
    Louisiana Tech University Louisiana Tech Digital Commons Doctoral Dissertations Graduate School Spring 2012 The effects of background noise on distortion product otoacoustic emissions and hearing screenings Amy E. Hollowell Louisiana Tech University Follow this and additional works at: https://digitalcommons.latech.edu/dissertations Part of the Speech Pathology and Audiology Commons Recommended Citation Hollowell, Amy E., "" (2012). Dissertation. 348. https://digitalcommons.latech.edu/dissertations/348 This Dissertation is brought to you for free and open access by the Graduate School at Louisiana Tech Digital Commons. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of Louisiana Tech Digital Commons. For more information, please contact [email protected]. THE EFFECTS OF BACKGROUND NOISE ON DISTORTION PRODUCT OTOACOUSTIC EMISSIONS AND HEARING SCREENINGS by Amy E. Hollowell, B.S. A Dissertation Presented in Partial Fulfillment of the Requirements of the Degree Doctor of Audiology COLLEGE OF LIBERAL ARTS LOUISIANA TECH UNIVERSITY May 2012 UMI Number: 3515927 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. DiygrMution UMI 3515927 Published by ProQuest LLC 2012. Copyright in the Dissertation held by the Author. Microform Edition © ProQuest LLC. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 LOUISIANA TECH UNIVERSITY THE GRADUATE SCHOOL 2/27/2012 Date We hereby recommend that the dissertation prepared under our supervision by Amy E.
    [Show full text]
  • Effects of Aircraft Noise Exposure on Heart Rate During Sleep in the Population Living Near Airports
    International Journal of Environmental Research and Public Health Article Effects of Aircraft Noise Exposure on Heart Rate during Sleep in the Population Living Near Airports Ali-Mohamed Nassur 1,*, Damien Léger 2, Marie Lefèvre 1, Maxime Elbaz 2, Fanny Mietlicki 3, Philippe Nguyen 3, Carlos Ribeiro 3, Matthieu Sineau 3, Bernard Laumon 4 and Anne-Sophie Evrard 1 1 Université Lyon, Université Claude Bernard Lyon1, IFSTTAR, UMRESTTE, UMR T_9405, F-69675 Bron, France; [email protected] (M.L.); [email protected] (A.-S.E.) 2 Université Paris Descartes, APHP, Hôtel-Dieu de Paris, Centre du Sommeil et de la Vigilance et EA 7330 VIFASOM, 75004 Paris, France; [email protected] (D.L.); [email protected] (M.E.) 3 Bruitparif, the Center for Technical Assessment of the Noise Environment in the Île-de-France Region of France, 93200 Saint-Denis, France; [email protected] (F.M.); [email protected] (P.N.); [email protected] (C.R.); [email protected] (M.S.) 4 IFSTTAR, Transport, Health and Safety Department, F-69675 Bron, France; [email protected] * Correspondence: [email protected] Received: 30 October 2018; Accepted: 15 January 2019; Published: 18 January 2019 Abstract: Background Noise in the vicinity of airports is a public health problem. Many laboratory studies have shown that heart rate is altered during sleep after exposure to road or railway noise. Fewer studies have looked at the effects of exposure to aircraft noise on heart rate during sleep in populations living near airports. Objective The aim of this study was to investigate the relationship between the sound pressure level (SPL) of aircraft noise and heart rate during sleep in populations living near airports in France.
    [Show full text]
  • Audio Processing Laboratory
    AC 2010-1594: A GRADUATE LEVEL COURSE: AUDIO PROCESSING LABORATORY Buket Barkana, University of Bridgeport Page 15.35.1 Page © American Society for Engineering Education, 2010 A Graduate Level Course: Audio Processing Laboratory Abstract Audio signal processing is a part of the digital signal processing (DSP) field in science and engineering that has developed rapidly over the past years. Expertise in audio signal processing - including speech signal processing- is becoming increasingly important for working engineers from diverse disciplines. Audio signals are stored, processed, and transmitted using digital techniques. Creating these technologies requires engineers that understand real-time application issues in the related areas. With this motivation, we designed a graduate level laboratory course which is Audio Processing Laboratory in the electrical engineering department in our school two years ago. This paper presents the status of the audio processing laboratory course in our school. We report the challenges that we have faced during the development of this course in our school and discuss the instructor’s and students’ assessments and recommendations in this real-time signal-processing laboratory course. 1. Introduction Many DSP laboratory courses are developed for undergraduate and graduate level engineering education. These courses mostly focus on the general signal processing techniques such as quantization, filter design, Fast Fourier Transformation (FFT), and spectral analysis [1-3]. Because of the increasing popularity of Web-based education and the advancements in streaming media applications, several web-based DSP Laboratory courses have been designed for distance education [4-8]. An internet-based signal processing laboratory that provides hands-on learning experiences in distributed learning environments has been developed by Spanias et.al[6] .
    [Show full text]
  • Why Use Signal-To-Noise As a Measure of MS Performance When It Is Often Meaningless?
    Why use Signal-To-Noise as a Measure of MS Performance When it is Often Meaningless? Technical Overview Authors Abstract Greg Wells, Harry Prest, and The signal-to-noise of a chromatographic peak determined from a single measurement Charles William Russ IV, has served as a convenient figure of merit used to compare the performance of two Agilent Technologies, Inc. different MS systems. The evolution in the design of mass spectrometry instrumenta- 2850 Centerville Road tion has resulted in very low noise systems that have made the comparison of perfor- Wilmington, DE 19809-1610 mance based upon signal-to-noise increasingly difficult, and in some modes of opera- USA tion impossible. This is especially true when using ultra-low noise modes such as high resolution mass spectrometry or tandem MS; where there are often no ions in the background and the noise is essentially zero. This occurs when analyzing clean stan- dards used to establish the instrument specifications. Statistical methodology com- monly used to establish method detection limits for trace analysis in complex matri- ces is a means of characterizing instrument performance that is rigorously valid for both high and low background noise conditions. Instrument manufacturers should start to provide customers an alternative performance metric in the form of instrument detection limits based on relative the standard deviation of replicate injections to allow analysts a practical means of evaluating an MS system. Introduction of polysiloxane at m/z 281 increased baseline noise for HCB at m/z 282). Signal-to-noise ratio (SNR) has been a primary standard for Improvement in instrument design and changes to test com- comparing the performance of chromatography systems includ- pounds were accompanied by a number of different ing GC/MS and LC/MS.
    [Show full text]
  • Robust Signal-To-Noise Ratio Estimation Based on Waveform Amplitude Distribution Analysis
    Robust Signal-to-Noise Ratio Estimation Based on Waveform Amplitude Distribution Analysis Chanwoo Kim, Richard M. Stern Department of Electrical and Computer Engineering and Language Technologies Institute Carnegie Mellon University, Pittsburgh, PA 15213 {chanwook, rms}@cs.cmu.edu speech and background noise are independent, (2) clean Abstract speech follows a gamma distribution with a fixed shaping In this paper, we introduce a new algorithm for estimating the parameter, and (3) the background noise has a Gaussian signal-to-noise ratio (SNR) of speech signals, called WADA- distribution. Based on these assumptions, it can be seen that if SNR (Waveform Amplitude Distribution Analysis). In this we model noise-corrupted speech at an unknown SNR using algorithm we assume that the amplitude distribution of clean the Gamma distribution, the value of the shaping parameter speech can be approximated by the Gamma distribution with obtained using maximum likelihood (ML) estimation depends a shaping parameter of 0.4, and that an additive noise signal is uniquely on the SNR. Gaussian. Based on this assumption, we can estimate the SNR While we assume that the background noise can be by examining the amplitude distribution of the noise- assumed to be Gaussian, we will demonstrate that this corrupted speech. We evaluate the performance of the algorithm still provides better results than the NIST STNR WADA-SNR algorithm on databases corrupted by white algorithm, even in the presence of other types of maskers such noise, background music, and interfering speech. The as background music or interfering speech, where the WADA-SNR algorithm shows significantly less bias and less corrupting signal is clearly not Gaussian.
    [Show full text]
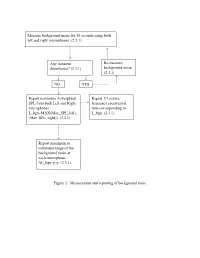
  • Figure 1. Measurement and Reporting of Background Noise
    Measure background noise for 10 seconds using both left and right microphones. (2.3.1) Any transient Re-measure disturbance? (2.3.1) background noise (2.3.1) NO YES Report maximum A-weighted Report 1/3 octave SPL from both Left and Right frequency spectrum at microphones. time corresponding to L_bgn=MAX(Max_SPL_left), L_bgn (2.3.1) (Max_SPL_right)) (2.3.1) Report maximum to minimum range of the background noise at each microphone. ǻL_bgn, p-p (2.3.1) Figure 1. Measurement and reporting of background noise. Conduct measurement according to 3.3 Is ǻL_bgn, p-p less or equal to 2 dB? (2.3.1) NO YES Is ǻL according to Table 1 Carry out SPL correction greater or equal to 10 dB? (2.3.2) according to Table 1 for each individual measurement j . (2.3.2) NO YES STOP. No valid measurement Report L_testcorr, j for each individual test run j. (2.3.2) Figure 2. Vehicle A-Weighted sound pressure level measurement correction criteria. Conduct measurement according to 3.3 Is background level in each one-third octave band of interest at least 6 dB greater than the corresponding one-third-octave band measured according to 2.3.1 ? (2.3.3) NO YES STOP. No valid Is overall sound pressure level measured according measurement of to 3.3 at least 10 dB greater than the corresponding one-third octave overall sound pressure level of the background band results noise measured according to 2.3.1 ? (2.3.3) NO YES STOP. No valid Report one-third-octave band measurement of results for each band of interest one-third octave for each individual test run j.
    [Show full text]
  • The Case of the Ile De France Region Presentation of Bruitparif
    The case of the Ile de France region Presentation of Bruitparif T&E conference, Quiet Please the future of EU noise Policy, 25 May 2011 Piotr Gaudibert Agenda ¾ Presentation of Bruitparif and context of the Ile-de-France region (Paris region) ¾ First results of noise assessment in Ile- de-France region in application of the END ¾ Actions in Ile-de-France region to fight road traffic noise ¾ Questions about the different ways to reduce noise at the source: example of the Paris action plan The Ile-de-France region ~ 11 million inhabitants = 19 % of the French population, ~ 30 % of the GNP characterised by the population ~ 12 000 km2 density of the Paris agglomeration : 87 % of inhabitants (9,75 millions) live in 23 % of the region’s area Inhabitants density Inhabitants/km2 area directly concerned by the END The Ile-de-France region ¾ Characterised by the number and density of infrastructures: ¾ More than 40,000 km of roads ¾ More than 1800 km of railways ¾ A unique aircraft system in Europe based on two international airports (Roissy CDG 544 000 mvts and Orly 233 000 mvts in 2007) + civil airfield of Le Bourget (58 000 mvts in 2005) and heliport of Issy-les-Mx + ~20 small airfields What is Bruitparif? ¾ A regional agency for assessing and monitoring noise in the Ile-de-France Region ¾ Created in october 2004 ¾ Coming into force at the end of year 2005 ¾ Reasons for creation: Noise = one of the major concerns for inhabitants of the Ile- de-France region Multiplicity of actors involved in noise management Lots of noise data but no common
    [Show full text]
  • A Guide to Office Acoustics
    A GUIDE TO OFFICE ACOUSTICS www.acousticguide.org www.thefis.org Acoustic rafts, allowing the soffit to be exposed while reducing reverberation. First edition published April 2011 A GUIDE TO This edition published April 2015 OFFICE ACOUSTICS ISBN 978-0-9565341-1-8 World copyright reserved Copyright © 2015 FIS Published by FIS No part of this document may be reproduced or transmitted in any form or by any means electronic, chemical or mechanical, including photocopying, any information storage or retrieval system without licence or other permission in writing from the copyright owner. While every care has been taken to ensure the accuracy of the details presented in this document, we regret that FIS cannot be held responsible for any errors or omissions contained herein. 2 3 Artwork provides absorption to reduce reverberation. CONTENTS 1 Foreword . .. .. .. .. .7 . 5 Design guide to office acoustics . 19. 6 Terminology . 43 2 Introduction . .. .. .. .. .9 . Acoustic control. 19 7 Case studies . .. .. .. 51. Ceilings . .22 3 Basic acoustics . .. .. .. .. 11. Partitions. 24 8 Standards . .. .. .. 63. Doors. 30 4 Noise in offices . .. .. .. 15. Raised access flooring . .31 9 Acoustic research . .. .. .65 . Acoustic cavity barriers . .32 Noise sources . .15 Screens and furniture. 33 10 Acknowledgements . .. .. .71 . Mandatory requirements. 17 Floorcoverings. 33 The role of the acoustician. 17 Secondary glazing. 33 Internal finishes. 34 Design considerations. 34 Flanking sound. 34 Sibilance and grazing reflections. 35 Ventilation . .35 Integrating acoustic absorption into building services systems . .36 Sound rating and performance descriptors . .36 Reverberation control . .36 Intelligibilty. 36 Open plan environments . .37 Cellular environments . .39 Atria. 39 Background noise. 39 Proprietary introduced sound masking.
    [Show full text]