DOCSLIB.ORG

Robust Signal-To-Noise Ratio Estimation Based on Waveform Amplitude Distribution Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Robust Signal-To-Noise Ratio Estimation Based on Waveform Amplitude Distribution Analysis Robust Signal-to-Noise Ratio Estimation Based on Waveform Amplitude Distribution Analysis Chanwoo Kim, Richard M. Stern Department of Electrical and Computer Engineering and Language Technologies Institute Carnegie Mellon University, Pittsburgh, PA 15213 {chanwook, rms}@cs.cmu.edu speech and background noise are independent, (2) clean Abstract speech follows a gamma distribution with a fixed shaping In this paper, we introduce a new algorithm for estimating the parameter, and (3) the background noise has a Gaussian signal-to-noise ratio (SNR) of speech signals, called WADA- distribution. Based on these assumptions, it can be seen that if SNR (Waveform Amplitude Distribution Analysis). In this we model noise-corrupted speech at an unknown SNR using algorithm we assume that the amplitude distribution of clean the Gamma distribution, the value of the shaping parameter speech can be approximated by the Gamma distribution with obtained using maximum likelihood (ML) estimation depends a shaping parameter of 0.4, and that an additive noise signal is uniquely on the SNR. Gaussian. Based on this assumption, we can estimate the SNR While we assume that the background noise can be by examining the amplitude distribution of the noise- assumed to be Gaussian, we will demonstrate that this corrupted speech. We evaluate the performance of the algorithm still provides better results than the NIST STNR WADA-SNR algorithm on databases corrupted by white algorithm, even in the presence of other types of maskers such noise, background music, and interfering speech. The as background music or interfering speech, where the WADA-SNR algorithm shows significantly less bias and less corrupting signal is clearly not Gaussian. variability with respect to the type of noise compared to the The organization of this paper is as follows: in Sec. 2 we standard NIST STNR algorithm. In addition, the algorithm is discuss the assumptions about clean speech and additive noise. quite computationally efficient. In Sec. 3 we describe how the SNR measurement can be Index Terms: SNR estimation, Gamma distribution, obtained from the amplitude distribution of the input signal. Gaussian distribution Section 4 contains experimental results that compare the accuracy of WADA-SNR to the standard NIST STNR algorithm. 1. Introduction The estimation of signal-to-noise ratios (SNRs) has been 2. Characterization of clean speech and extensively investigated for decades and it is still an active additive noise field of research (e.g. [1-7]). Reliable SNR estimation can improve algorithms for speech enhancement [1][2], speech It is widely known that the symmetric gamma distribution detection, and speech recognition [3], since knowledge of is a good approximation to the amplitude distribution of a SNR makes it easier to compensate for the effects of noise. large speech corpus (e.g. [8][9]). Specifically, the probability Techniques for estimating SNR can be classified into density function, f (x) of clean speech can be represented by several categories. One of the approaches is based on x the following equation [8-11]: distinguishing the spectra of noise and speech. Noise spectrum estimation (e.g. [3]) or spectral subtraction techniques usually belong to this category. Another approach f (x | ) x | x | x 1 exp( | x |) (1) x x x x is based on measurement of the energy. The widely used 2 ( x ) NIST STNR (Signal-To-Noise-Ratio) algorithm is based on this technique. In this approach, a histogram of short-time where x is the amplitude of the speech, and x and !x are the energy is constructed, from which the signal and noise energy shaping and rate parameters of the gamma distribution, distributions are estimated. In another approach, Martin [4] respectively [10][11]. Fig. 1 (a) illustrates this property. Many used the low-energy envelope in frequency bands to estimate research results show that values of 0.4 or 0.5 for x provide the SNR level. Still other approaches are based on statistics the best fit for clean speech (e.g. [8][9]). We will assume for that are obtained from waveform samples rather than from now that a clean speech signal x[n] exhibits a gamma energy or spectral coefficients. For example, Nemer [5] used distribution with a fixed shaping parameter x of 0.4 and an kurtosis values to estimate the SNR in each frequency band. arbitrary value of !x. (The parameter !x serves to normalize In this approach, short-time voiced signals in a given the density function and has no impact on the SNR frequency band are assumed to be sinusoidal with a fixed estimation.) As will be shown later (cf. Fig. 2), the SNR phase, and short-time unvoiced signals in this band is value estimated by our algorithm is relatively independent of assumed to be a sinusoidal signal with random phase. x if the true value of the SNR is less than 20 dB. Throughout Our approach is based on the fact that the amplitude this paper, x[n], *[n], and z[n] will denote sample functions distribution of a waveform usually can be characterized by a for clean speech, noise, and corrupt speech respectively. The gamma distribution with a shaping parameter value between variables x, , and z will denote sample values without regard 0.4 and 0.5. This fact has been observed by several research to time, and x, *, and z will represent the random variables groups and has been described in numerous books and papers that describe them. (e.g. [8][9]). The only assumptions we make are that (1) the Copyright © 2008 ISCA Accepted after peer review of full paper 2598 September 22-26, Brisbane Australia 100 2 =0.4 Actual Speech Amplitude Distribution x =0.44 Gamma Distribution Model x 1.5 80 x=0.54 z 1 60 G 40 0.5 Probability Density Probability 20 0 -20 0 20 40 60 80 100 SNR (dB) Figure 2: Calculated dependence of the parameter Gz on 0 0 0.02 0.04 0.06 0.08 0.1 the SNR in dB. Amplitude (Maximum Possible Amplitude Is Normalized to 1.0) (a) Clean speech corrupt speech signal z[n] is represented by the following equation: 100 z[n] x[n] [n] (3) Actual Speech Amplitude Distribution Gamma Distribution Model From (1) and (2), the power of the speech and noise 80 parts can be obtained from the above distributions using some arithmetic: ( 1) 60 P x x (4) x 2 x P 2 (5) 40 * * where Px and Pv are the signal and noise power, respectively. Probability Density Probability Hence, the SNR of this signal z[n] is given by 20 Px x ( x 1) (6) z 2 P* ( * x ) 0 0 0.02 0.04 0.06 0.08 0.1 Amplitude (Maximum Possible Amplitude Is Normalized to 1.0) 3. SNR measurement based on the gamma (b) 10-dB additive white Gaussian noise distribution 100 In Figs. 1(a) to 1(c), we observe the amplitude distribution of Actual Speech Amplitude Distribution clean and corrupt utterances. It can be seen that even for noisy Gamma Distribution Model 80 speech utterances, the gamma distribution model is still quite close to the actual amplitude distribution. More importantly, we can easily see that the shapes of Figs. 1(b) and 1(c) are 60 very different from that of Fig. 1(a). Hence we observe that the value of the parameter z characterizes the amplitude distribution of noisy speech using the Gamma-function model 40 depends on the SNR. From the probability density function of the gamma distribution, we can obtain the following relation Probability Density Probability 20 for corrupt speech [11]: N 1 N 1 1 1 (7) ln( z ) 0 ( z ) ln( B| z[n] |) Bln[| z[n] |] N N 0 n 0 n 0 0 0.02 0.04 0.06 0.08 0.1 where () is the digamma function. Amplitude (Maximum Possible Amplitude Is Normalized to 1.0) 0 z (c) 0-dB additive white Gaussian noise From the above equation, we can see that the shaping Figure 1: Comparison between the actual amplitude parameter depends on the right hand side of (7). Based on this distribution of speech and the gamma distribution model. observation, we define the parameter Gz: N1 N1 A subset of 1,600 utterances of the DARPA RM test set 1 1 (8) Gz ln( B| z[n] |) Bln(| z[n] |) was used. N n0 N n0 We now show that Gz in (8) can be employed to uniquely If a clean speech signal is corrupted by additive Gaussian determine SNRs. Let us assume that |z[n]| and ln(|z[n]|) are noise *[n], its probability density function can be expressed as: both ergodic in the mean. For N sufficiently large, we can 1 2 (2) replace the time averages by their corresponding ensemble f ( ) exp( ) * 2 averages: 2 * 2 * 1 N1 where * is the standard deviation of the noise. B| z[n] | E[| z |] (9) We will further assume that both x[n] and *[n] have zero N n0 means and that they are statistically independent. The 2599 50 White Noise Background Music Noise 40 Interfering Speaker Noise Ideal Case 30 20 10 Estimated SNR [dB] Figure 3: The structure of the WADA-SNR estimation system 0 1 N 1 (10) -10 Bln | z[n] | E[ln | z |] -10-50 5 1015202530 N n0 True SNR [dB] producing: G ln(E[| z |]) E(ln(| z |)) (a) Results with the WADA-SNR algorithm Z . (11) ln(E[| x * |]) E(ln(| x * |)) 50 Let’s consider the following normalized random variables ~x ~ and* : 40 ~ x xx, (12) ~ 30 * * / * (13) From (1), (2), (12), and (13), we see that the probability ~ 20 densities of ~x and * are represented by the following distributions: ~ 10 x dx 1 ~ ~ X 1 ~ (14) f~ (x) f ( ) | x | exp( | x |) [dB] SNR Peak Estimated x x ~ White Noise X dx 2 ( x ) 0 Background Music Noise Interfering Speaker Noise ~ ~ d 1 ~2 f~ ( ) f ( ) exp( ) (15) Ideal Case (7dB Difference Assumption) * * * ~ -10 d 2 -10 -5 0 5 10 15 20 25 30 Note that Eqs.
Load more

Recommended publications
  • Blind Denoising Autoencoder
    1 Blind Denoising Autoencoder Angshul Majumdar In recent times a handful of papers have been published on Abstract—The term ‘blind denoising’ refers to the fact that the autoencoders used for signal denoising [10-13]. These basis used for denoising is learnt from the noisy sample itself techniques learn the autoencoder model on a training set and during denoising. Dictionary learning and transform learning uses the trained model to denoise new test samples. Unlike the based formulations for blind denoising are well known. But there has been no autoencoder based solution for the said blind dictionary learning and transform learning based approaches, denoising approach. So far autoencoder based denoising the autoencoder based methods were not blind; they were not formulations have learnt the model on a separate training data learning the model from the signal at hand. and have used the learnt model to denoise test samples. Such a The main disadvantage of such an approach is that, one methodology fails when the test image (to denoise) is not of the never knows how good the learned autoencoder will same kind as the models learnt with. This will be first work, generalize on unseen data. In the aforesaid studies [10-13] where we learn the autoencoder from the noisy sample while denoising. Experimental results show that our proposed method training was performed on standard dataset of natural images performs better than dictionary learning (K-SVD), transform (image-net / CIFAR) and used to denoise natural images. Can learning, sparse stacked denoising autoencoder and the gold the learnt model be used to recover images from other standard BM3D algorithm.
    [Show full text]
  • A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers
    Sensors 2011, 11, 9233-9241; doi:10.3390/s111009233 OPEN ACCESS sensors ISSN 1424-8220 www.mdpi.com/journal/sensors Article A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers Albert Canagasabey 1,2,*, Andrew Michie 1,2, John Canning 1, John Holdsworth 3, Simon Fleming 2, Hsiao-Chuan Wang 1,2 and Mattias L. Åslund 1 1 Interdisciplinary Photonics Laboratories (iPL), School of Chemistry, University of Sydney, 2006, NSW, Australia; E-Mails: [email protected] (A.M.); [email protected] (J.C.); [email protected] (H.-C.W.); [email protected] (M.L.Å.) 2 Institute of Photonics and Optical Science (IPOS), School of Physics, University of Sydney, 2006, NSW, Australia; E-Mail: [email protected] (S.F.) 3 SMAPS, University of Newcastle, Callaghan, NSW 2308, Australia; E-Mail: [email protected] (J.H.) * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +61-2-9351-1984. Received: 17 August 2011; in revised form: 13 September 2011 / Accepted: 23 September 2011 / Published: 27 September 2011 Abstract: Linewidth measurements of a distributed feedback (DFB) fibre laser are made using delayed self heterodyne interferometry (DHSI) with both Mach-Zehnder and Michelson interferometer configurations. Voigt fitting is used to extract and compare the Lorentzian and Gaussian linewidths and associated sources of noise. The respective measurements are wL (MZI) = (1.6 ± 0.2) kHz and wL (MI) = (1.4 ± 0.1) kHz. The Michelson with Faraday rotator mirrors gives a slightly narrower linewidth with significantly reduced error.
    [Show full text]
  • Effect of Moisture Distribution on Velocity and Waveform of Ultrasonic-Wave Propagation in Mortar
    materials Article Effect of Moisture Distribution on Velocity and Waveform of Ultrasonic-Wave Propagation in Mortar Shinichiro Okazaki 1,* , Hiroma Iwase 2, Hiroyuki Nakagawa 3, Hidenori Yoshida 1 and Ryosuke Hinei 4 1 Faculty of Engineering and Design, Kagawa University, 2217-20 Hayashi, Takamatsu, Kagawa 761-0396, Japan; [email protected] 2 Chuo Consultants, 2-11-23 Nakono, Nishi-ku, Nagoya, Aichi 451-0042, Japan; [email protected] 3 Shikoku Research Institute Inc., 2109-8 Yashima, Takamatsu, Kagawa 761-0113, Japan; [email protected] 4 Building Engineering Group, Civil Engineering and Construction Department, Shikoku Electric Power Co., Inc., 2-5 Marunouchi, Takamatsu, Kagawa 760-8573, Japan; [email protected] * Correspondence: [email protected] Abstract: Considering that the ultrasonic method is applied for the quality evaluation of concrete, this study experimentally and numerically investigates the effect of inhomogeneity caused by changes in the moisture content of concrete on ultrasonic wave propagation. The experimental results demonstrate that the propagation velocity and amplitude of the ultrasonic wave vary for different moisture content distributions in the specimens. In the analytical study, the characteristics obtained experimentally are reproduced by modeling a system in which the moisture content varies between the surface layer and interior of concrete. Keywords: concrete; ultrasonic; water content; elastic modulus Citation: Okazaki, S.; Iwase, H.; 1. Introduction Nakagawa, H.; Yoshida, H.; Hinei, R. Effect of Moisture Distribution on As many infrastructures deteriorate at an early stage, long-term structure management Velocity and Waveform of is required. If structural deterioration can be detected as early as possible, the scale of Ultrasonic-Wave Propagation in repair can be reduced, decreasing maintenance costs [1].
    [Show full text]
  • Bernoulli-Gaussian Distribution with Memory As a Model for Power Line Communication Noise Victor Fernandes, Weiler A
    XXXV SIMPOSIO´ BRASILEIRO DE TELECOMUNICAC¸ OES˜ E PROCESSAMENTO DE SINAIS - SBrT2017, 3-6 DE SETEMBRO DE 2017, SAO˜ PEDRO, SP Bernoulli-Gaussian Distribution with Memory as a Model for Power Line Communication Noise Victor Fernandes, Weiler A. Finamore, Mois´es V. Ribeiro, Ninoslav Marina, and Jovan Karamachoski Abstract— The adoption of Additive Bernoulli-Gaussian Noise very useful to come up with a as simple as possible models (ABGN) as an additive noise model for Power Line Commu- of PLC noise, similar to the additive white Gaussian noise nication (PLC) systems is the subject of this paper. ABGN is a (AWGN) model. model that for a fraction of time is a low power noise and for the remaining time is a high power (impulsive) noise. In this context, In this regard, we introduce the definition of a simple and we investigate the usefulness of the ABGN as a model for the useful mathematical model for the noise perturbing the data additive noise in PLC systems, using samples of noise registered transmission over PLC channel that would be a helpful tool. during a measurement campaign. A general procedure to find the With this goal in mind, an investigation of the usefulness of model parameters, namely, the noise power and the impulsiveness what we call additive Bernoulli-Gaussian noise (ABGN) as a factor is presented. A strategy to assess the noise memory, using LDPC codes, is also examined and we came to the conclusion that model for the noise perturbing the digital communication over ABGN with memory is a consistent model that can be used as for PLC channel is discussed.
    [Show full text]
  • Introduction to Noise Radar and Its Waveforms
    sensors Article Introduction to Noise Radar and Its Waveforms Francesco De Palo 1, Gaspare Galati 2 , Gabriele Pavan 2,* , Christoph Wasserzier 3 and Kubilay Savci 4 1 Department of Electronic Engineering, Tor Vergata University of Rome, now with Rheinmetall Italy, 00131 Rome, Italy; [email protected] 2 Department of Electronic Engineering, Tor Vergata University and CNIT-Consortium for Telecommunications, Research Unit of Tor Vergata University of Rome, 00133 Rome, Italy; [email protected] 3 Fraunhofer Institute for High Frequency Physics and Radar Techniques FHR, 53343 Wachtberg, Germany; [email protected] 4 Turkish Naval Research Center Command and Koc University, Istanbul, 34450 Istanbul,˙ Turkey; [email protected] * Correspondence: [email protected] Received: 31 July 2020; Accepted: 7 September 2020; Published: 11 September 2020 Abstract: In the system-level design for both conventional radars and noise radars, a fundamental element is the use of waveforms suited to the particular application. In the military arena, low probability of intercept (LPI) and of exploitation (LPE) by the enemy are required, while in the civil context, the spectrum occupancy is a more and more important requirement, because of the growing request by non-radar applications; hence, a plurality of nearby radars may be obliged to transmit in the same band. All these requirements are satisfied by noise radar technology. After an overview of the main noise radar features and design problems, this paper summarizes recent developments in “tailoring” pseudo-random sequences plus a novel tailoring method aiming for an increase of detection performance whilst enabling to produce a (virtually) unlimited number of noise-like waveforms usable in different applications.
    [Show full text]
  • EP Signal to Noise in Emp 2
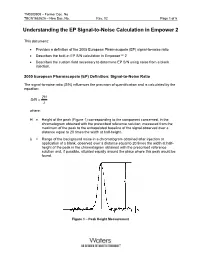
    TN0000909 – Former Doc. No. TECN1852625 – New Doc. No. Rev. 02 Page 1 of 5 Understanding the EP Signal-to-Noise Calculation in Empower 2 This document: • Provides a definition of the 2005 European Pharmacopeia (EP) signal-to-noise ratio • Describes the built-in EP S/N calculation in Empower™ 2 • Describes the custom field necessary to determine EP S/N using noise from a blank injection. 2005 European Pharmacopeia (EP) Definition: Signal-to-Noise Ratio The signal-to-noise ratio (S/N) influences the precision of quantification and is calculated by the equation: 2H S/N = λ where: H = Height of the peak (Figure 1) corresponding to the component concerned, in the chromatogram obtained with the prescribed reference solution, measured from the maximum of the peak to the extrapolated baseline of the signal observed over a distance equal to 20 times the width at half-height. λ = Range of the background noise in a chromatogram obtained after injection or application of a blank, observed over a distance equal to 20 times the width at half- height of the peak in the chromatogram obtained with the prescribed reference solution and, if possible, situated equally around the place where this peak would be found. Figure 1 – Peak Height Measurement TN0000909 – Former Doc. No. TECN1852625 – New Doc. No. Rev. 02 Page 2 of 5 In Empower 2 software, the EP Signal-to-Noise (EP S/N) is determined in an automated fashion and does not require a blank injection. The intention of this calculation is to preserve the sense of the EP calculation without requiring a separate blank injection.
    [Show full text]
  • Measurement and Estimation of the Mode Partition Coefficient K
    Measurement and Estimation of the Mode Partition Coefficient k Rick Pimpinella and Jose Castro IEEE P802.3bm 40 Gb/s and 100 Gb/s Fiber Optic Task Force November 2012, San Antonio, TX Background & Objective Background: Mode Partition Noise in MMF channel links is caused by pulse-to-pulse power fluctuations among VCSEL modes and differential delay due to dispersion in the fiber (Power independent penalty) “k” is an index used to describe the degree of mode fluctuations and takes on a value between 0 and 1, called the mode partition coefficient [1,2] Currently the IEEE link model assumes k = 0.3 It has been discussed that a new link model requires validation of k The measurement & estimation of k is challenging due to several conditions: Low sensitivity of detectors at 850nm The presence of additional noise components in VCSEL-MMF channels (RIN, MN, Jitter – intensity fluctuations, reflection noise, thermal noise, …) Differences in VCSEL designs Objective: Provide an experimental estimate of the value of k for VCSELs Additional work in progress 2 MPN Theory Originally derived for Fabry-Perot lasers and SMF [3] Assumptions: Total power of all modes carried by each pulse is constant Power fluctuations among modes are anti-correlated Mechanism: When modes (different wavelengths) travel at the same speed their fluctuations remain anti-correlated and the resultant pulse-to-pulse noise is zero. When modes travel in a dispersive medium the modes undergo different delays resulting in pulse distortions and a noise penalty. Example: Two VCSEL modes transmitted in a SMF undergoing chromatic dispersion: START END Optical Waveform @ Detector START t END With mode power fluctuations Decision Region Shorter Wavelength Time (arrival) t slope DL Time (arrival) Longer Wavelength Time (arrival) 3 Example of Intensity Fluctuation among VCSEL modes MPN can be observed using an Optical Spectrum Analyzer (OSA).
    [Show full text]
  • Introduction to Noise Measurements on Business Machines (Bo0125)
    BO 0125-11 Introduction to Noise Measurements on Business Machines by Roger Upton, B.Sc. Introduction In recent years, manufacturers of DIN 45 635 pt.19 ization committees in the pursuit of business machines, that is computing ANSI Si.29, (soon to be superced- harmonization, meaning that the stan- and office machines, have come under ed by ANSI S12.10) dards agree with each other in the increasing pressure to provide noise ECMA 74 bulk of their requirements. This appli- data on their products. For instance, it ISO/DIS 7779 cation note first discusses some acous- is becoming increasingly common to tic measurement parameters, and then see noise levels advertised, particular- With four separate standards in ex- the measurements required by the ly for printers. A number of standards istence, one might expect some con- various standards. Finally, it describes have been written governing how such siderable divergence in their require- some Briiel & Kjaer measurement sys- noise measurements should be made, ments. However, there has been close terns capable of making the required namely: contact between the various standard- measurements. Introduction to Noise Measurement Parameters The standards referred to in the previous section call for measure• ments of sound power and sound pres• sure. These measurements can then be used in a variety of ways, such as noise labelling, prediction of installation noise levels, comparison of noise emis• sions of products, and production con• trol. Sound power and sound pressure are fundamentally different quanti• ties. Sound power is a measure of the ability of a device to make noise. It is independent of the acoustic environ• ment.
    [Show full text]
  • The Physics of Sound 1
    The Physics of Sound 1 The Physics of Sound Sound lies at the very center of speech communication. A sound wave is both the end product of the speech production mechanism and the primary source of raw material used by the listener to recover the speaker's message. Because of the central role played by sound in speech communication, it is important to have a good understanding of how sound is produced, modified, and measured. The purpose of this chapter will be to review some basic principles underlying the physics of sound, with a particular focus on two ideas that play an especially important role in both speech and hearing: the concept of the spectrum and acoustic filtering. The speech production mechanism is a kind of assembly line that operates by generating some relatively simple sounds consisting of various combinations of buzzes, hisses, and pops, and then filtering those sounds by making a number of fine adjustments to the tongue, lips, jaw, soft palate, and other articulators. We will also see that a crucial step at the receiving end occurs when the ear breaks this complex sound into its individual frequency components in much the same way that a prism breaks white light into components of different optical frequencies. Before getting into these ideas it is first necessary to cover the basic principles of vibration and sound propagation. Sound and Vibration A sound wave is an air pressure disturbance that results from vibration. The vibration can come from a tuning fork, a guitar string, the column of air in an organ pipe, the head (or rim) of a snare drum, steam escaping from a radiator, the reed on a clarinet, the diaphragm of a loudspeaker, the vocal cords, or virtually anything that vibrates in a frequency range that is audible to a listener (roughly 20 to 20,000 cycles per second for humans).
    [Show full text]
  • Airspace: Seeing Sound Grades
    National Aeronautics and Space Administration GRADES K-8 Seeing Sound airspace Aeronautics Research Mission Directorate Museum in a BO SerieXs www.nasa.gov MUSEUM IN A BOX Materials: Seeing Sound In the Box Lesson Overview PVC pipe coupling Large balloon In this lesson, students will use a beam of laser light Duct tape to display a waveform against a flat surface. In doing Super Glue so, they will effectively“see” sound and gain a better understanding of how different frequencies create Mirror squares different sounds. Laser pointer Tripod Tuning fork Objectives Tuning fork activator Students will: 1. Observe the vibrations necessary to create sound. Provided by User Scissors GRADES K-8 Time Requirements: 30 minutes airspace 2 Background The Science of Sound Sound is something most of us take for granted and rarely do we consider the physics involved. It can come from many sources – a voice, machinery, musical instruments, computers – but all are transmitted the same way; through vibration. In the most basic sense, when a sound is created it causes the molecule nearest the source to vibrate. As this molecule is touching another molecule it causes that molecule to vibrate too. This continues, from molecule to molecule, passing the energy on as it goes. This is also why at a rock concert, or even being near a car with a large subwoofer, you can feel the bass notes vibrating inside you. The molecules of your body are vibrating, allowing you to physically feel the music. MUSEUM IN A BOX As with any energy transfer, each time a molecule vibrates or causes another molecule to vibrate, a little energy is lost along the way, which is why sound gets quieter with distance (Fig 1.) and why louder sounds, which cause the molecules to vibrate more, travel farther.
    [Show full text]
  • 33600A Series Trueform Waveform Generators Generate Trueform Arbitrary Waveforms with Less Jitter, More Fidelity and Greater Resolution
    DATA SHEET 33600A Series Trueform Waveform Generators Generate Trueform arbitrary waveforms with less jitter, more fidelity and greater resolution Revolutionary advances over previous generation DDS 33600A Series waveform generators with exclusive Trueform signal generation technology offer more capability, fidelity and flexibility than previous generation Direct Digital Synthesis (DDS) generators. Use them to accelerate your development Trueform process from start to finish. – 1 GSa/s sampling rate and up to 120 MHz bandwidth Better Signal Integrity – Arbs with sequencing and up to 64 MSa memory – 1 ps jitter, 200x better than DDS generators – 5x lower harmonic distortion than DDS – Compatible with Keysight Technologies, DDS Inc. BenchVue software Over the past two decades, DDS has been the waveform generation technology of choice in function generators and economical arbitrary waveform generators. Reduced Jitter DDS enables waveform generators with great frequency resolution, convenient custom waveforms, and a low price. <1 ps <200 ps As with any technology, DDS has its limitations. Engineers with exacting requirements have had to either work around the compromised performance or spend up to 5 times more for a high-end, point-per-clock waveform generator. Keysight Technologies, Inc. Trueform Trueform technology DDS technology technology offers an alternative that blends the best of DDS and point-per-clock architectures, giving you the benefits of both without the limitations of either. Trueform technology uses an exclusive digital 0.03%
    [Show full text]
  • Background Noise, Noise Sensitivity, and Attitudes Towards Neighbours, and a Subjective Experiment Using a Rubber Ball Impact Sound
    International Journal of Environmental Research and Public Health Article Background Noise, Noise Sensitivity, and Attitudes towards Neighbours, and a Subjective Experiment Using a Rubber Ball Impact Sound Jeongho Jeong Fire Insurers Laboratories of Korea, 1030 Gyeongchungdae-ro, Yeoju-si 12661, Korea; [email protected]; Tel.: +82-31-887-6737 Abstract: When children run and jump or adults walk indoors, the impact sounds conveyed to neighbouring households have relatively high energy in low-frequency bands. The experience of and response to low-frequency floor impact sounds can differ depending on factors such as the duration of exposure, the listener’s noise sensitivity, and the level of background noise in housing complexes. In order to study responses to actual floor impact sounds, it is necessary to investigate how the response is affected by changes in the background noise and differences in the response when focusing on other tasks. In this study, the author presented subjects with a rubber ball impact sound recorded from different apartment buildings and housings and investigated the subjects’ responses to varying levels of background noise and when they were assigned tasks to change their level of attention on the presented sound. The subjects’ noise sensitivity and response to their neighbours were also compared. The results of the subjective experiment showed differences in the subjective responses depending on the level of background noise, and high intensity rubber ball impact sounds were associated with larger subjective responses. In addition, when subjects were performing a Citation: Jeong, J. Background Noise, task like browsing the internet, they attended less to the rubber ball impact sound, showing a less Noise Sensitivity, and Attitudes towards Neighbours, and a Subjective sensitive response to the same intensity of impact sound.
    [Show full text]