Einstein College of Engineering
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

AN-MISC-032 Date Issued: 5/24/16 Revision: REV
APPLICATION NOTE This information provided by Automationdirect.com Technical Support Team is provided “as is” without a guarantee of any kind. This document is provided to offer assistance in using our products. We do not guarantee that the contents are suitable for your particular application, nor do we assume any responsibility for applying the contents to your application. Subject: Transient Suppression Guidelines for AutomationDirect PLCs Number: AN-MISC-032 Date Issued: 5/24/16 Revision: REV. A Transient Suppression for Inductive Loads in a Control System This Application Note is intended to give a quick overview of the negative effects of transient voltages on a control system and provide some simple advice on how to effectively minimize them. The need for transient suppression is often not apparent to the newcomers in the automation world. Many mysterious errors that can afflict an installation can be traced back to a lack of transient suppression. What is a Transient Voltage and Why is it Bad? Inductive loads (devices with a coil) generate transient voltages as they transition from being energized to being de-energized. If not suppressed, the transient can be many times greater than the voltage applied to the coil. These transient voltages can damage PLC outputs or other electronic devices connected to the circuit, and cause unreliable operation of other electronics in the general area. Transients must be managed with suppressors for long component life and reliable operation of the control system. This example shows a simple circuit with a small 24V/125mA/3W relay. As you can see, when the switch is opened, thereby de-energizing the coil, the transient voltage generated across the switch contacts peaks at 140V! Example: Circuit with no Suppression Oscilloscope Volts 160 140 120 100 + 80 24 VDC 60 - Relay Coil 40 (24V/125mA/3W, 20 AutomationDirect part no. -

Basic DC Motor Circuits
Basic DC Motor Circuits Living with the Lab Gerald Recktenwald Portland State University [email protected] DC Motor Learning Objectives • Explain the role of a snubber diode • Describe how PWM controls DC motor speed • Implement a transistor circuit and Arduino program for PWM control of the DC motor • Use a potentiometer as input to a program that controls fan speed LWTL: DC Motor 2 What is a snubber diode and why should I care? Simplest DC Motor Circuit Connect the motor to a DC power supply Switch open Switch closed +5V +5V I LWTL: DC Motor 4 Current continues after switch is opened Opening the switch does not immediately stop current in the motor windings. +5V – Inductive behavior of the I motor causes current to + continue to flow when the switch is opened suddenly. Charge builds up on what was the negative terminal of the motor. LWTL: DC Motor 5 Reverse current Charge build-up can cause damage +5V Reverse current surge – through the voltage supply I + Arc across the switch and discharge to ground LWTL: DC Motor 6 Motor Model Simple model of a DC motor: ❖ Windings have inductance and resistance ❖ Inductor stores electrical energy in the windings ❖ We need to provide a way to safely dissipate electrical energy when the switch is opened +5V +5V I LWTL: DC Motor 7 Flyback diode or snubber diode Adding a diode in parallel with the motor provides a path for dissipation of stored energy when the switch is opened +5V – The flyback diode allows charge to dissipate + without arcing across the switch, or without flowing back to ground through the +5V voltage supply. -

FAGOR Avalanche Rectifiers
Application Note Fagor Electrónica Semiconductores Avalanche Rectifiers Avalanche Rectifiers are diodes that can tolerate voltages above the repetitive reverse maximum blocking voltage (Vrrm) and, furthermore, dissipate a specified maximum energy during these pulses. Here we describe how these diodes differ from normal rectifiers and the applications to which they are suited. Introduction Rectifiers are two-terminal devices that are used to conduct current in one direction but block in the other according to a characteristic of the type shown in Figure 1. Standard rectifiers operate stably in either the Reverse Blocking Mode or in the Forward Conducting Mode. In the first case, only a very small leakage current flows so that power dissipation in the device is not important. In the second case, the forward voltage is more than a volt so considerable power may be dissipated in the device, but provided the heat is extracted efficiently the junction temperature will not exceed the maximum rated value and the device will be stable. I Figure 1 Modes of Operation within the I-V characteristic of Rectifiers. V Forward Concucting Avalanche Reverse Blocking Mode Mode Mode Further limitations apply when the rectifier is switched from conducting a large forward current to blocking a large reverse voltage. During a time after switching, the current that flows in the reverse direction greatly exceeds the reverse leakage value. Even if the delay in establishing the blocking condition is not important in the application, the additional power dissipated may cause the device to overheat and eventually fail. The recovery time depends strongly on the forward current before switching but standard conditions have been established to measure the Trr parameter (Typically: I F=0.5A switched to I R=1A at t=0 and recuperation defined has having occurred when I R=0.25A). -

Datasheet Search Engine
Power Modules PRODUCT GUIDE CONTENTS 1. Product List 3 2. Introduction to the Products and Their Features 4 3. Structure and Dimensions 5 4. Power Module Packages 6 5. System Diagram of Power Module Products 6 6. Power Module Product Matrix 7 7. Product Line-ups Listed by Package 8 Power Transistor Modules S-10 Series MP4005~, MP4101~ 8 S-12 Series MP4301~, MP6301 9 F-12 Series MP4501~, MP6901 10 Power MOSFET Modules S-10M Series MP4208~ 11 S-12M Series MP4410~, MP6404 12 F-12M Series MP4711 13 8. Toshiba Power Module Products 14 9. Applications and Line-ups 15 10. Typical Applications 20 11. Dimensions of Power Module Packages 21 12. Power Module Packing 22 13. Final-Phase Production List 23 14. List of Discontinued Products 23 External Appeaiance of Power Modules Discrete power devices Power modules PNP × 3 + NPN × 3 (NPN or PNP) × 4 + flyback diode × 4 2 Product List Product No. Page Product No. Page MP4005 8 MP4411 12 MP4006 8 MP4412 12 MP4009 8 MP4501 10 Power Modules MP4013 8 MP4502 10 MP4015 8 MP4503 10 MP4020 8 MP4504 10 MP4021 8 MP4506 10 MP4024 8 MP4507 10 MP4025 8 MP4508 10 MP4101 8 MP4513 10 MP4104 8 MP4514 10 MP4208 11 MP4711 13 MP4209 11 MP6301 9 MP4210 11 MP6404 12 MP4211 11 MP6901 10 MP4212 11 MP4301 9 MP4303 9 MP4304 9 MP4305 9 MP4410 12 3 Introduction to the Products and Their Features Stru Rapid advances are being made in the miniaturization and level of integration of electronic devices, not only in the signal processing stages but also in the power stages. -

Reactive Power Support Capability of Flyback Micro- Inverter with Pseudo
Reactive Power Support Capability of Flyback Micro- inverter with Pseudo-dc Link by Edwin Fonkwe Fongang MSc, Masdar Institute of Science and Technology (2013) Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degree of Master of Science at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY June 2015 © Massachusetts Institute of Technology, MMXV. All rights reserved. Author________________________________________________________________________ Department of Electrical Engineering and Computer Science May 20, 2015 Certified by____________________________________________________________________ James L. Kirtley Professor of Electrical Engineering Thesis Supervisor Accepted by____________________________________________________________________ Professor Leslie A. Kolodziejski Chair of the Department Committee on Graduate Students Reactive Power Support Capability of Flyback Micro-inverter with Pseudo-dc Link by Edwin Fonkwe Fongang Submitted to the Department of Electrical Engineering and Computer Science On May 20, 2015, in partial fulfillment of the requirements for the degree of Master of Science Abstract The flyback micro-inverter with a pseudo-dc link has traditionally been used for injecting only active power in to the power distribution network. In this thesis, a new approach will be proposed to control the micro-inverter to supply reactive power to the grid which is important for grid voltage support. Circuit models and mathematical analyses are developed to explain -

High Step-Up Forward Flyback Converter with Nondissipative Snubber for Solar Energy Application
ISSN (Print) : 2320 – 3765 ISSN (Online): 2278 – 8875 International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering (An ISO 3297: 2007 Certified Organization) Vol. 4, Issue 7, July 2015 High Step-Up Forward Flyback Converter with Nondissipative Snubber for Solar Energy Application Divya Dileep Kumar1, Maheswaran. K2 PG Student [PED], Dept. of EEE, Nehru College of Engineering and Research Centre, Thrissur, Kerala, India1 Assistant Professor, Dept. of EEE, Nehru College of Engineering and Research Centre, Thrissur, Kerala, India2 ABSTRACT: A high step-up forward flyback converter with nondissipative snubber for solar energy application is introduced here. High gain DC/DC converters are the key part of renewable energy systems .The designing of high gain DC/DC converters is imposed by severe demands. It produces high step-up voltage gain by using a forward flyback converter. The energy in the coupled inductor leakage inductance can be recycled via a nondissipative snubber on the primary side. It consists of a combination of forward and flyback converter on the secondary side. It is a hybrid type of forward and flyback converter, sharing the transformer for increasing the utilization factor. By stacking the outputs of them, extremely high voltage gain can be obtained with small volume and high efficiency even with a galvanic isolation. The separated secondary windings in low turn-ratio reduce the voltage stress of the secondary rectifiers, contributing to achievement of high efficiency. Here presents a high step-up topology employing a series connected forward flyback converter, which has a series connected output for high boosting voltage-transfer gain. -

Micropower Direct Power Glossary
MICROPOWER DIRECT Glossary Of Power Conversion Terms Alternating Voltage: A voltage that periodically switches direction of flow from positive to negative. — A — The average value of an AC voltage, for a pure sine Absolute Maximum Ratings: Peak perfor- wave, is zero. One cycle (or period) is the time it mance ratings for a power supply. If exceeded, takes the voltage to rise to its maximum value in one permanent damage to a power supply could direction, return to zero, rise to its maximum value in occur. When specified, these specifications are not the opposite direction and again, return to zero. The given as continuous ratings, and proper operation number of cycles per second is the AC frequency. is not implied. Ambient Air: The air mass immediately surround- AC: Abbreviation for alternating current. See Al- ing an operating power supply. Reliable operation ternating Current. of power supplies requires sufficient surrounding air AC/DC: Abbreviation for alternating current/ mass and flow to prevent thermal runaway caused direct current. by heat dissipated by the supply. AC Current: See Alternating Current. Ambient Temperature: The average tem- perature of air immediately surrounding a power AC Front-End: Part of a distributed power system. Temperature measurements should be system that will convert ac line voltage to a made about 0.5 inches from the body of the power semiregulated dc voltage level. An AC front-end supply. See Operating Temperature and Storage will typically provide power factor correction and Temperature. universal (~85 VAC to 265 VAC) ac compatibility. An ac front-end’s output voltage is usually 350 Ambient Temperature Range: The tempera- VDC to 400 VDC. -

Designing for Loss of Ground on Texas Instruments High-Side
www.ti.com Table of Contents Application Report Designing for Loss of Ground and Loss of Battery on Texas Instruments High-Side Switches Timothy Logan ABSTRACT A loss of ground fault is an erroneous condition on the power design of a system where the reference to ground is disconnected and lost from the system. This can be caused by several different events such as a physical severing of the ground connection or a faulty external wiring being introduced to the power rail. If not properly addressed during the design phase, a loss of ground fault can not only cause damage to the attached power components of a system but also to valuable upstream components such as microcontrollers or logic arrays. A loss of battery condition is when the connection from the high side switch to the upstream power supply is lost. In this fault condition proper design precautions must be taken in order to protect against special loading conditions such as inductive turnoff. In this application note a few key design insights are examined to protect against both loss of ground and loss of battery faults when using Texas Instruments smart high-side switch products. Table of Contents 1 Loss of Ground Conditions................................................................................................................................................... 2 1.1 Loss of Device Ground.......................................................................................................................................................2 1.2 Loss of Module Ground......................................................................................................................................................3 -

Inductive Load Arc Suppression Application Note
Application Note: Inductive Load Arc Suppression Figure 2. Introduction Bidirectional TVS Diode When a reed switch or reed sensor is used to control an Reed Switch/Sensor inductive device (relay coil, solenoid, transformer, small motor, etc.), the energy stored in the inductance in the device Load will subject the switch contacts to a high voltage when the reed switch opens. When the switch contacts open, the contact gap is initially small. Arcing across this contact gap RL can occur immediately after the switch opens. This can TVS Vs happen in resistive as well as inductive loads, but inductive loads generate a higher voltage and this causes increased L arcing. Increased arcing decreases switch life. Direct current (DC) inductive circuits typically use a diode to prevent the high voltage. The diode in the circuit is called a suppression diode, flyback diode, freewheeling diode, or catch diode. However, a diode cannot be used in an alternating current (AC) circuit. AC arc suppression requires the use of a RC suppression has the advantage of limiting the switch metal-oxide varistor (MOV), a bidirectional transient voltage contact voltage at the time of switch opening when the suppressor (TVS) diode, or an RC suppression network. An size of the contact gap is small. RC suppression can also RC suppression network is also called a snubber. The various be used to reduce arcing and improve life in resistive arc suppression methods have various advantages and loads. With RC suppression, a seriesconnected capacitor disadvantages. Using no suppression is also an option if life and resistor network is placed across (in parallel with) the is adequate without it. -

Reliability Analysis of Power Electronic Devices
Tesi di Dottorato Universita` degli Studi di Napoli \Federico II" Dipartimento di Ingegneria Elettrica e delle Tecnologie dell'Informazione Dottorato di Ricerca in Ingegneria Elettronica e delle Telecomunicazioni Reliability Analysis of Power Electronic Devices GIUSEPPE DE FALCO Il Coordinatore del Corso di Dottorato Il Tutore Ch.mo Prof. Niccol`o Rinaldi Ch.mo Prof. Andrea Irace A. A. 2014{2015 Acknowledgements I want to express my gratitude to my Tutor, Prof. Andrea Irace for his support in the PhD studies, and without whom I could have never get to the conclusion of my works. His support and skills in the subject I have dealt with have been very precious-less. I also want to thank Prof. Breglio for having shared his competences and motivations to the work. Many thanks go to Dr. Michele Riccio who I have always considered as a co-Tutor for the indications he has given to me. CONTENTS v Contents List of Figures viii List of Tables xii Introduction xiii Chapter 1 : Physics of Semiconductor Devices 1 1.1 The Power MOSFET . 1 1.1.1 Basic structure . 2 1.1.2 Static characteristics . 4 1.1.3 On state conduction losses of the VDMOS . 7 1.1.4 Transient Characteristics . 9 1.1.5 Safe Operating Area . 13 1.2 The Insulated Gate Bipolar Transistor (IGBT) . 16 1.2.1 Basic structure . 16 1.2.2 Device operation . 17 1.2.3 Static Characteristic . 20 1.2.4 Transient Characteristic . 22 1.2.5 Latch-up of Parasitic Thyristor . 25 1.2.6 Safe Operating Area . -

Automatic Monitoring and Interleaved Flyback Inverter for PV Applications
IOSR Journal of Electrical and Electronics Engineering (IOSR-JEEE) e-ISSN: 2278-1676,p-ISSN: 2320-3331, Volume 11, Issue 6 Ver. I (Nov. – Dec. 2016), PP 79-86 www.iosrjournals.org Automatic Monitoring and Interleaved Flyback Inverter for PV Applications Ms Viji Chandran1, Mrs Edwina D Rodrigues2, Mr Santhosh Raj3 1(Departmen of EEE, College of Engineering, Perumon/ CUSAT, India) 2(Department of EEE, College of Engineering, Perumon/ CUSAT, India) 3 (Department of EEE, College of Engineering, Perumon/ CUSAT, India) Abstract: The utilization of solar energy in proper ways offers huge potential for natural resources, economy and for the expansion of renewable energies on the road to a future oriented energy supply. The growing importance of power consumption in today’s appliances leads to new research works on the converter area .The dc-dc converters primarily strive for efficiency , with new technologies playing a role to achieve that goal .The project paper demonstrates analysis and design of converter systems to develop a high efficient dc- dc converter. Efficiency is an important factor while considering dc-dc converter characteristics. It affects the physical package sizes of both power supply and the entire system and has direct effect on the system’s operating temperature and reliability .A desired converter should be small and light weight with low system cost. The paper introduces an efficient flyback converter for PV applications. The flyback topology has a benefit to work under high power with reduced cost and size of working elements .The use of three interleaving cells in flyback topology enhance its use under high frequency applications with reduced size of filtering elements . -
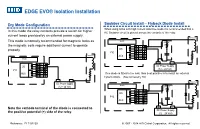
EDGE EVO® Isolation Installation
EDGE EVO® Isolation Installation Dry Mode Configuration Snubber Circuit Install – Flyback Diode Install When using locks with high current inductive loads it is recommended that a In this mode the relay contacts provide a switch for higher RC Snubber circuit is placed across the contacts of the relay. current loads provided by an external power supply. Relay Coil EH400 This mode is normally recommended for magnetic locks as Snubber Circuit the magnetic coils require additional current to operate NC properly. DS COM P10 NO NC Relay Coil AUX COM EH400 NO + - NC DS COM DC Power Supply P10 NO (12 – 24 Volt) NC AUX COM If no diode is fitted to the lock, then best practice is to install an external NO flyback diode. (See Accessory Kit) + - Relay Coil DC Power Supply EH400 (12 – 24 Volt) Snubber Circuit NC DS COM P10 NO NC AUX COM NO Note the cathode terminal of the diode is connected to + - DC Power Supply the positive potential (+) side of the relay. (12 – 24 Volt) Reference: PLT-02139 © 2007 - 2014 HID Global Corporation. All rights reserved. EDGE EVO® Isolation Installation Wet Mode Configuration Flyback Diode Installation (See Accessory Kit) Wet mode provides a source of power at voltages ranging The recommended position for the diode is at the inductive between 12 and 24 volts. The current supplied is dependent load. If this is not possible the diode can be placed at the on the voltage being supported as well as the source of the product connector. power. Large inductive loads can inject negative spikes into Relay Coil the power supply.