JPEG-Resistant Adversarial Images
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Exploring the .BMP File Format
Exploring the .BMP File Format Don Lancaster Synergetics, Box 809, Thatcher, AZ 85552 copyright c2003 as GuruGram #14 http://www.tinaja.com [email protected] (928) 428-4073 The .BMP image standard is used by Windows and elsewhere to represent graphics images in any of several different display and compression options. The .BMP advantages are that each pixel is usually independently available for any alteration or modification. And that repeated use does not normally degrade the image. Because lossy compression is not used. Its main disadvantage is that file sizes are usually horrendous compared to JPEG, fractal, GIF, or other lossy compression schemes. A comparison of popular image standards can be found here. I’ve long been using the .BMP format for my eBay and my other phototography, scanning, and post processing. I firmly believe that… All photography, scanning, and all image post-processing should always be done using .BMP or a similar non-lossy format. Only after all post-processing is complete should JPEG or another compressed distribution format be chosen. Some current examples of my .BMP work now do include the IMAGIMAG.PDF post-processing tutorial, the Bitmap Typewriterthat generates fully anti-aliased small fonts, the Aerial Photo Combiner, and similar utilities and tutorials found on our Fonts & Images, PostScript, and on our Acrobat library pages. A few projects of current interest involving .BMP files include true view camera swings and tilts for a digital camera, distortion correction, dodging & burning, preventing white punchthrough on knockouts, and emphasis vignetting. Mainly applied to uncompressed RGBX 24-bit color .BMP files. -

Free Lossless Image Format
FREE LOSSLESS IMAGE FORMAT Jon Sneyers and Pieter Wuille [email protected] [email protected] Cloudinary Blockstream ICIP 2016, September 26th DON’T WE HAVE ENOUGH IMAGE FORMATS ALREADY? • JPEG, PNG, GIF, WebP, JPEG 2000, JPEG XR, JPEG-LS, JBIG(2), APNG, MNG, BPG, TIFF, BMP, TGA, PCX, PBM/PGM/PPM, PAM, … • Obligatory XKCD comic: YES, BUT… • There are many kinds of images: photographs, medical images, diagrams, plots, maps, line art, paintings, comics, logos, game graphics, textures, rendered scenes, scanned documents, screenshots, … EVERYTHING SUCKS AT SOMETHING • None of the existing formats works well on all kinds of images. • JPEG / JP2 / JXR is great for photographs, but… • PNG / GIF is great for line art, but… • WebP: basically two totally different formats • Lossy WebP: somewhat better than (moz)JPEG • Lossless WebP: somewhat better than PNG • They are both .webp, but you still have to pick the format GOAL: ONE FORMAT THAT COMPRESSES ALL IMAGES WELL EXPERIMENTAL RESULTS Corpus Lossless formats JPEG* (bit depth) FLIF FLIF* WebP BPG PNG PNG* JP2* JXR JLS 100% 90% interlaced PNGs, we used OptiPNG [21]. For BPG we used [4] 8 1.002 1.000 1.234 1.318 1.480 2.108 1.253 1.676 1.242 1.054 0.302 the options -m 9 -e jctvc; for WebP we used -m 6 -q [4] 16 1.017 1.000 / / 1.414 1.502 1.012 2.011 1.111 / / 100. For the other formats we used default lossless options. [5] 8 1.032 1.000 1.099 1.163 1.429 1.664 1.097 1.248 1.500 1.017 0.302� [6] 8 1.003 1.000 1.040 1.081 1.282 1.441 1.074 1.168 1.225 0.980 0.263 Figure 4 shows the results; see [22] for more details. -
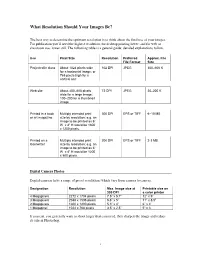
What Resolution Should Your Images Be?
What Resolution Should Your Images Be? The best way to determine the optimum resolution is to think about the final use of your images. For publication you’ll need the highest resolution, for desktop printing lower, and for web or classroom use, lower still. The following table is a general guide; detailed explanations follow. Use Pixel Size Resolution Preferred Approx. File File Format Size Projected in class About 1024 pixels wide 102 DPI JPEG 300–600 K for a horizontal image; or 768 pixels high for a vertical one Web site About 400–600 pixels 72 DPI JPEG 20–200 K wide for a large image; 100–200 for a thumbnail image Printed in a book Multiply intended print 300 DPI EPS or TIFF 6–10 MB or art magazine size by resolution; e.g. an image to be printed as 6” W x 4” H would be 1800 x 1200 pixels. Printed on a Multiply intended print 200 DPI EPS or TIFF 2-3 MB laserwriter size by resolution; e.g. an image to be printed as 6” W x 4” H would be 1200 x 800 pixels. Digital Camera Photos Digital cameras have a range of preset resolutions which vary from camera to camera. Designation Resolution Max. Image size at Printable size on 300 DPI a color printer 4 Megapixels 2272 x 1704 pixels 7.5” x 5.7” 12” x 9” 3 Megapixels 2048 x 1536 pixels 6.8” x 5” 11” x 8.5” 2 Megapixels 1600 x 1200 pixels 5.3” x 4” 6” x 4” 1 Megapixel 1024 x 768 pixels 3.5” x 2.5” 5” x 3 If you can, you generally want to shoot larger than you need, then sharpen the image and reduce its size in Photoshop. -

JPEG File Interchange Format Version 1.02
JPEG File Interchange Format Version 1.02 September 1, 1992 Eric Hamilton C-Cube Microsystems 1778 McCarthy Blvd. Milpitas, CA 95035 +1 408 944-6300 Fax: +1 408 944-6314 E-mail: [email protected] JPEG File Interchange Format Version 1.02 Why a File Interchange Format JPEG File Interchange Format is a minimal file format which enables JPEG bitstreams to be exchanged between a wide variety of platforms and applications. This minimal format does not include any of the advanced features found in the TIFF JPEG specification or any application specific file format. Nor should it, for the only purpose of this simplified format is to allow the exchange of JPEG compressed images. JPEG File Interchange Format features • Uses JPEG compression • Uses JPEG interchange format compressed image representation • PC or Mac or Unix workstation compatible • Standard color space: one or three components. For three components, YCbCr (CCIR 601-256 levels) • APP0 marker used to specify Units, X pixel density, Y pixel density, thumbnail • APP0 marker also used to specify JFIF extensions • APP0 marker also used to specify application-specific information JPEG Compression Although any JPEG process is supported by the syntax of the JPEG File Interchange Format (JFIF) it is strongly recommended that the JPEG baseline process be used for the purposes of file interchange. This ensures maximum compatibility with all applications supporting JPEG. JFIF conforms to the JPEG Draft International Standard (ISO DIS 10918-1). The JPEG File Interchange Format is entirely compatible with the standard JPEG interchange format; the only additional requirement is the mandatory presence of the APP0 marker right after the SOI marker. -

Using Graphics on the Web Keep Graphics Small Most Users Have Little Patience for Slow Loading Pages, and Will Rapidly Abandon a Slow Site
Using graphics on the web Keep graphics small Most users have little patience for slow loading pages, and will rapidly abandon a slow site. Remember that many of your audience will be using a dial up modem, and try to keep graphics file sizes under 40K. Be willing to sacrifice some image quality. Provide thumbnails for large graphics If you feel your site absolutely requires large graphics, to illustrate an experimental set-up for example, provide an in-line reduced thumbnail of the graphic on your main page, which will link to the larger graphic and a separate page. This way the user has a choice and can decide if she or he wants to view it then, at another time or at all. It's also a kindness to indicate the file size, so the user can estimate how long the display will take to load. Use the same motifs throughout your site Recycle graphics (icons, navigation bars), as they are cached locally once downloaded. Standardizing on a set of graphic arrows, bullets, logos etc. also provides your site with a characteristic "look and feel" that your audience can identify with. Provide alternative text for non-graphics browsers Use the [alt="" ] command to provide a text description for those with text-only browsers or those who may have graphics loading disabled on their browsers. This also follows guidelines for Americans with Disabilities Act (ADA) Compliance. Use the appropriate file format Graphics Interchange format - GIF - was originally developed for the rapid transfer of images. GIF compression works by encoding the identical repeating elements within any given graphic, storing the code in an attached table and using the data to display the image when called upon by the web browser. -

Understanding Image Formats and When to Use Them
Understanding Image Formats And When to Use Them Are you familiar with the extensions after your images? There are so many image formats that it’s so easy to get confused! File extensions like .jpeg, .bmp, .gif, and more can be seen after an image’s file name. Most of us disregard it, thinking there is no significance regarding these image formats. These are all different and not cross‐ compatible. These image formats have their own pros and cons. They were created for specific, yet different purposes. What’s the difference, and when is each format appropriate to use? Every graphic you see online is an image file. Most everything you see printed on paper, plastic or a t‐shirt came from an image file. These files come in a variety of formats, and each is optimized for a specific use. Using the right type for the right job means your design will come out picture perfect and just how you intended. The wrong format could mean a bad print or a poor web image, a giant download or a missing graphic in an email Most image files fit into one of two general categories—raster files and vector files—and each category has its own specific uses. This breakdown isn’t perfect. For example, certain formats can actually contain elements of both types. But this is a good place to start when thinking about which format to use for your projects. Raster Images Raster images are made up of a set grid of dots called pixels where each pixel is assigned a color. -

JPEG Standard
JPEG standard JPEG: “Joint Photographic Experts Group” Formally: ISO/IEC JTC1/SC29/WG10 Working Group 10 International (JBIG, JPEG) Organization for Subcommittee 29 Standardization Joint ISO/IEC (Coding of Audio, Technical International Picture, Multimedia Committee Electrotechnical and Hypermedia (Information Commission Information) Technology) Joint effort with CCITT (International Telephone and Telegraph Consultative Committee, now ITU-T) Study Group VIII Work commenced in 1986 International standard ISO/IEC 10918-1 and CCITT Rec. T.81 in 1992 Widely used for image exchange, WWW, and digital photography Motion-JPEG is de facto standard for digital video editing Bernd Girod: EE398A Image and Video Compression JPEG standard no. 1 JPEG: image partition into 8x8 block 8x8 blocks Padding of right boundary blocks Padding of lower boundary blocks Bernd Girod: EE398A Image and Video Compression JPEG standard no. 2 Baseline JPEG coder DC Huffman tables dc quantization indices Differential coding VLC Level 8x8 Uniform Compressed scalar image data input offset DCT quantization image Zig-zag Run-level scan coding VLC Compressed image data ac quantization indices Quantization tables AC Huffman tables Bernd Girod: EE398A Image and Video Compression JPEG standard no. 3 Recommended quantization tables Based on psychovisual threshold experiments Luminance Chrominance, subsampled 2:1 16 11 10 16 24 40 51 61 17 18 24 47 99 99 99 99 12 12 14 19 26 58 60 55 18 21 26 66 99 99 99 99 14 13 16 24 40 57 69 56 24 26 56 99 99 99 99 99 14 17 22 29 51 87 80 62 47 66 99 99 99 99 99 99 18 22 37 56 68 109 103 77 99 99 99 99 99 99 99 99 24 36 55 64 81 104 113 92 99 99 99 99 99 99 99 99 49 64 78 87 103 121 120 101 99 99 99 99 99 99 99 99 72 92 95 98 112 100 103 99 99 99 99 99 99 99 99 99 [JPEG Standard, Annex K] Bernd Girod: EE398A Image and Video Compression JPEG standard no. -

On the Efficiency of the Wavelet Based Compression Techniques
IS&T©s 2001 PICS Conference Proceedings On the Efficiency of the Wavelet Based Compression Techniques £ ? ¾ B. Smolka M. Szlezak K.N. Plataniotis A. N. Venetsanopoulos ½ Silesian University of Technology, Department of Automatic Control, Akademicka 16 Str, 44-101 Gliwice, Poland, ¾ Edward S. Rogers Sr. Department of Electrical and Computer Engineering University of Toronto. 10 King’s College Road, Toronto, Canada, ? Abstract structured correlated errors typical to JPEG and wavelet In this paper we address the problem of the correlation be- based compression methods (Fig. 1, Tab. 1, Fig. 4). To as- tween the objective quality measures, like mean squared sess the efficiency of the three losssy compression methods error or signal to noise ratio and the subjective quality per- a joint subjective and objective study was undertaken. ceived by human viewers. Using both the objective and For the experiments a set of 3 gray-scale and 3 color subjective quality measures we aimed to compare the effi- test images was used (Fig. 2). The images were com- ciency of the wavelet based lossy codecs DJVU and LWF pressed at nearly the same compression ratios and the stan- with the DCT based standard JPEG compression method. dard quality measures like RMS, MSE, SNR and PSNR For the experiments a set of 3 gray-scale and 3 color were calculated for all images at different compression lev- test images was used. The images were encoded at the els. same compression levels and standard objective quality mea- For the visual assessment of the quality of the com- sures were calculated for all images. -
![Arxiv:2101.00973V1 [Eess.IV] 30 Dec 2020 Ternet Users Mainly Communicated in the Form of Plain Text, Reduce the Data Size [8]](https://docslib.b-cdn.net/cover/9655/arxiv-2101-00973v1-eess-iv-30-dec-2020-ternet-users-mainly-communicated-in-the-form-of-plain-text-reduce-the-data-size-8-839655.webp)
Arxiv:2101.00973V1 [Eess.IV] 30 Dec 2020 Ternet Users Mainly Communicated in the Form of Plain Text, Reduce the Data Size [8]
TOWARDS ROBUST DATA HIDING AGAINST (JPEG) COMPRESSION: A PSEUDO-DIFFERENTIABLE DEEP LEARNING APPROACH Chaoning Zhang∗, Adil Karjauv∗, Philipp Benz∗, In So Kweon [email protected], [email protected], [email protected], [email protected] ABSTRACT in the compressed form, such as JPEG or MPEG. This kind Data hiding is one widely used approach for protecting au- of lossy operation can easily destroy the hidden information thentication and ownership. Most multimedia content like for most existing data hiding approaches [1, 2]. Thus, robust images and videos are transmitted or saved in the compressed data hiding in multimedia that can resist non-malicious attack, form. This kind of lossy compression, such as JPEG, can de- lossy compression, has become a hot research direction. stroy the hidden data, which raises the need of robust data Recently, deep learning has also shown large success in hiding. It is still an open challenge to achieve the goal of data hiding data in images [3, 4, 5, 6, 7]. For improving the robust- hiding that can be against these compressions. Recently, deep ness against JPEG compression, the SOTA approaches need learning has shown large success in data hiding, while non- to include the JPEG compression in the training process [6, 7]. differentiability of JPEG makes it challenging to train a deep The challenge of this task is that JPEG compression is non- pipeline for improving robustness against lossy compression. differentiable. Prior works have either roughly simulated the The existing SOTA approaches replace the non-differentiable JPEG compression [6] or carefully designed the differentiable parts with differentiable modules that perform similar oper- function to mimic every step of the JPEG compression [7]. -

Image Formats
Image Formats Ioannis Rekleitis Many different file formats • JPEG/JFIF • Exif • JPEG 2000 • BMP • GIF • WebP • PNG • HDR raster formats • TIFF • HEIF • PPM, PGM, PBM, • BAT and PNM • BPG CSCE 590: Introduction to Image Processing https://en.wikipedia.org/wiki/Image_file_formats 2 Many different file formats • JPEG/JFIF (Joint Photographic Experts Group) is a lossy compression method; JPEG- compressed images are usually stored in the JFIF (JPEG File Interchange Format) >ile format. The JPEG/JFIF >ilename extension is JPG or JPEG. Nearly every digital camera can save images in the JPEG/JFIF format, which supports eight-bit grayscale images and 24-bit color images (eight bits each for red, green, and blue). JPEG applies lossy compression to images, which can result in a signi>icant reduction of the >ile size. Applications can determine the degree of compression to apply, and the amount of compression affects the visual quality of the result. When not too great, the compression does not noticeably affect or detract from the image's quality, but JPEG iles suffer generational degradation when repeatedly edited and saved. (JPEG also provides lossless image storage, but the lossless version is not widely supported.) • JPEG 2000 is a compression standard enabling both lossless and lossy storage. The compression methods used are different from the ones in standard JFIF/JPEG; they improve quality and compression ratios, but also require more computational power to process. JPEG 2000 also adds features that are missing in JPEG. It is not nearly as common as JPEG, but it is used currently in professional movie editing and distribution (some digital cinemas, for example, use JPEG 2000 for individual movie frames). -

What's the Diff Between a Jpeg and a Tiff?
WHAT’S THE DIFF BETWEEN A JPEG AND A TIFF? You’ve just scanned a photo into your computer. Now you need to save the image. You click on File > Save As... > and up pops a window with a menu of obscure acronyms: GIF, JPEG, BMP, TIF, EPS, PSD, PDF and more. What do they mean? What diff erence does it make? GIF. The letters “GIF” stand for “Graphics Interchange Format”. It is a low-resolution graphics fi le format for use on the Internet, often used in simple animated graphics. Images copied from the Internet are either GIFs or JPEGs and are almost always 72 dpi (dots per square inch). These low resolution graphics should NOT be used for high-resolution printing. JPEG or JPG. The letters “JPEG” stand for “Joint Photographic Experts Group”. It is a standardized image compression format that makes fi les smaller for quick transfer over a network and for display on the Inter- net. Most JPEGs are saved at 72 dpi, too low for high quality printing. The JPEG fi le format is acceptable as long as images are saved at 300 dpi or higher. (NOTE: Many digital cameras record photos as large 72 dpi JPEG images - anywhere from 8x12” up to 24x36”. In PhotoShop, they can be “resampled” to a smaller size and a higher resolution in order to create 300 dpi images.) BMP. The letters “BMP” stand for “bitmap”, a fi le format best suited for “line art” (i.e. images that do not have a dot-pattern or screen). Cartoons or drawings should be scanned at 600 dpi or higher and saved as a BMP in order to preserve sharp lines and shapes. -

JBIG-Like Coding of Bi-Level Image Data in JPEG-2000
ISO/IEC JTC 1/SC 29/WG1 N1014 Date: 1998-10- 20 ISO/IEC JTC 1/SC 29/WG 1 (ITU-T SG8) Coding of Still Pictures JBIG JPEG Joint Bi-level Image Joint Photographic Experts Group Experts Group TITLE: Report on Core Experiment CodEff26: JBIG-Like Coding of Bi-Level Image Data in JPEG-2000 SOURCE: Faouzi Kossentini ([email protected]) and Dave Tompkins Department of ECE, University of BC, Vancouver, BC, Canada V6T 1Z4 Soeren Forchhammer ([email protected]), Bo Martins and Ole Jensen Department of Telecommunication, TDU, Lyngby, Denmark, DK-2800 Ian Caven, Image Power Inc., Vancouver, BC, Canada V6E 4B1 Paul Howard, AT&T Labs, NJ, USA PROJECT: JPEG-2000 STATUS: Core Experiment Results REQUESTED ACTION: Discussion DISTRIBUTION: 14th Meeting of ISO/IEC JTC1/SC 29/WG1 Contact: ISO/IEC JTC 1/SC 29/WG 1 Convener - Dr. Daniel T. Lee Hewlett-Packard Company, 11000 Wolfe Road, MS42U0, Cupertion, California 95014, USA Tel: +1 408 447 4160, Fax: +1 408 447 2842, E-mail: [email protected] 2 1. Update This document updates results previously reported in WG1N863. Specifically, the upcoming JBIG-2 Verification Model (VM) was used to generate the compression rates in Table 1. These results more accurately reflect the expected bit rates, and include the overhead required for the proper JBIG-2 bitstream formatting. Results may be better in the final implementation, but these results are guaranteed to be attainable with the current VM. The JBIG-2 VM will be available in December 1998. 2. Summary This document presents experimental results that compare the compression performance several JBIG-like coders to the VM0 baseline coder.