Calculus with Proofs Assignment 10 Due on Thursday, April 8 by 11:59Pm Via Crowdmark
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Mean Value Theorem Math 120 Calculus I Fall 2015
The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0. -

Chapter 9 Optimization: One Choice Variable
RS - Ch 9 - Optimization: One Variable Chapter 9 Optimization: One Choice Variable 1 Léon Walras (1834-1910) Vilfredo Federico D. Pareto (1848–1923) 9.1 Optimum Values and Extreme Values • Goal vs. non-goal equilibrium • In the optimization process, we need to identify the objective function to optimize. • In the objective function the dependent variable represents the object of maximization or minimization Example: - Define profit function: = PQ − C(Q) - Objective: Maximize - Tool: Q 2 1 RS - Ch 9 - Optimization: One Variable 9.2 Relative Maximum and Minimum: First- Derivative Test Critical Value The critical value of x is the value x0 if f ′(x0)= 0. • A stationary value of y is f(x0). • A stationary point is the point with coordinates x0 and f(x0). • A stationary point is coordinate of the extremum. • Theorem (Weierstrass) Let f : S→R be a real-valued function defined on a compact (bounded and closed) set S ∈ Rn. If f is continuous on S, then f attains its maximum and minimum values on S. That is, there exists a point c1 and c2 such that f (c1) ≤ f (x) ≤ f (c2) ∀x ∈ S. 3 9.2 First-derivative test •The first-order condition (f.o.c.) or necessary condition for extrema is that f '(x*) = 0 and the value of f(x*) is: • A relative minimum if f '(x*) changes its sign y from negative to positive from the B immediate left of x0 to its immediate right. f '(x*)=0 (first derivative test of min.) x x* y • A relative maximum if the derivative f '(x) A f '(x*) = 0 changes its sign from positive to negative from the immediate left of the point x* to its immediate right. -

Critical Points and Classifying Local Maxima and Minima Don Byrd, Rev
Notes on Textbook Section 4.1 Critical Points and Classifying Local Maxima and Minima Don Byrd, rev. 25 Oct. 2011 To find and classify critical points of a function f (x) First steps: 1. Take the derivative f ’(x) . 2. Find the critical points by setting f ’ equal to 0, and solving for x . To finish the job, use either the first derivative test or the second derivative test. Via First Derivative Test 3. Determine if f ’ is positive (so f is increasing) or negative (so f is decreasing) on both sides of each critical point. • Note that since all that matters is the sign, you can check any value on the side you want; so use values that make it easy! • Optional, but helpful in more complex situations: draw a sign diagram. For example, say we have critical points at 11/8 and 22/7. It’s usually easier to evaluate functions at integer values than non-integers, and it’s especially easy at 0. So, for a value to the left of 11/8, choose 0; for a value to the right of 11/8 and the left of 22/7, choose 2; and for a value to the right of 22/7, choose 4. Let’s say f ’(0) = –1; f ’(2) = 5/9; and f ’(4) = 5. Then we could draw this sign diagram: Value of x 11 22 8 7 Sign of f ’(x) negative positive positive ! ! 4. Apply the first derivative test (textbook, top of p. 172, restated in terms of the derivative): If f ’ changes from negative to positive: f has a local minimum at the critical point If f ’ changes from positive to negative: f has a local maximum at the critical point If f ’ is positive on both sides or negative on both sides: f has neither one For the above example, we could tell from the sign diagram that 11/8 is a local minimum of f (x), while 22/7 is neither a local minimum nor a local maximum. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Calculus 120, Section 7.3 Maxima & Minima of Multivariable Functions
Calculus 120, section 7.3 Maxima & Minima of Multivariable Functions notes by Tim Pilachowski A quick note to start: If you’re at all unsure about the material from 7.1 and 7.2, now is the time to go back to review it, and get some help if necessary. You’ll need all of it for the next three sections. Just like we had a first-derivative test and a second-derivative test to maxima and minima of functions of one variable, we’ll use versions of first partial and second partial derivatives to determine maxima and minima of functions of more than one variable. The first derivative test for functions of more than one variable looks very much like the first derivative test we have already used: If f(x, y, z) has a relative maximum or minimum at a point ( a, b, c) then all partial derivatives will equal 0 at that point. That is ∂f ∂f ∂f ()a b,, c = 0 ()a b,, c = 0 ()a b,, c = 0 ∂x ∂y ∂z Example A: Find the possible values of x, y, and z at which (xf y,, z) = x2 + 2y3 + 3z 2 + 4x − 6y + 9 has a relative maximum or minimum. Answers : (–2, –1, 0); (–2, 1, 0) Example B: Find the possible values of x and y at which fxy(),= x2 + 4 xyy + 2 − 12 y has a relative maximum or minimum. Answer : (4, –2); z = 12 Notice that the example above asked for possible values. The first derivative test by itself is inconclusive. The second derivative test for functions of more than one variable is a good bit more complicated than the one used for functions of one variable. -

Summary of Derivative Tests
Summary of Derivative Tests Note that for all the tests given below it is assumed that the function f is continuous. Critical Numbers Definition. A critical number of a function f is a number c in the domain of f such that either f 0(c) = 0 or f 0(c) does not exist. Critical numbers tell you where a possible max/min occurs. Closed Interval Method Use: To find absolute mins/maxes on an interval [a; b] Steps: 1. Find the critical numbers of f [set f 0(x) = 0 and solve] 2. Find the value of f at each critical number 3. Find the value of f at each endpoint [i.e., find f(a) and f(b)] 4. Compare all of the above function values. The largest one is the absolute max and the smallest one is the absolute min. First Derivative Test Use: To find local max/mins Statement of the test: Suppose c is a critical number. 1. If f 0 changes from positive to negative at c; then f has a local max at c 2. If f 0 changes from negative to positive at c, then f has a local min at c 3. If f 0 is positive to the left and right of c [or negative to the left and right of c], then f has no local max or min at c Trick to Remember: If you are working on a problem and forget what means what in the above test, draw a picture of tangent lines around a minimum or around a maximum 1 Steps: 1. -

Just the Definitions, Theorem Statements, Proofs On
MATH 3333{INTERMEDIATE ANALYSIS{BLECHER NOTES 55 Abbreviated notes version for Test 3: just the definitions, theorem statements, proofs on the list. I may possibly have made a mistake, so check it. Also, this is not intended as a REPLACEMENT for your classnotes; the classnotes have lots of other things that you may need for your understanding, like worked examples. 6. The derivative 6.1. Differentiation rules. Definition: Let f :(a; b) ! R and c 2 (a; b). If the limit lim f(x)−f(c) exists and is finite, then we say that f is differentiable at x!c x−c 0 df c, and we write this limit as f (c) or dx (c). This is the derivative of f at c, and also obviously equals lim f(c+h)−f(c) by setting x = c + h or h = x − c. If f is h!0 h differentiable at every point in (a; b), then we say that f is differentiable on (a; b). Theorem 6.1. If f :(a; b) ! R is differentiable at at a point c 2 (a; b), then f is continuous at c. Proof. If f is differentiable at c then f(x) − f(c) f(x) = (x − c) + f(c) ! f 0(c)0 + f(c) = f(c); x − c as x ! c. So f is continuous at c. Theorem 6.2. (Calculus I differentiation laws) If f; g :(a; b) ! R is differentiable at a point c 2 (a; b), then (1) f(x) + g(x) is differentiable at c and (f + g)0(c) = f 0(c) + g0(c). -

MATH 162: Calculus II Differentiation
MATH 162: Calculus II Framework for Mon., Jan. 29 Review of Differentiation and Integration Differentiation Definition of derivative f 0(x): f(x + h) − f(x) f(y) − f(x) lim or lim . h→0 h y→x y − x Differentiation rules: 1. Sum/Difference rule: If f, g are differentiable at x0, then 0 0 0 (f ± g) (x0) = f (x0) ± g (x0). 2. Product rule: If f, g are differentiable at x0, then 0 0 0 (fg) (x0) = f (x0)g(x0) + f(x0)g (x0). 3. Quotient rule: If f, g are differentiable at x0, and g(x0) 6= 0, then 0 0 0 f f (x0)g(x0) − f(x0)g (x0) (x0) = 2 . g [g(x0)] 4. Chain rule: If g is differentiable at x0, and f is differentiable at g(x0), then 0 0 0 (f ◦ g) (x0) = f (g(x0))g (x0). This rule may also be expressed as dy dy du = . dx x=x0 du u=u(x0) dx x=x0 Implicit differentiation is a consequence of the chain rule. For instance, if y is really dependent upon x (i.e., y = y(x)), and if u = y3, then d du du dy d (y3) = = = (y3)y0(x) = 3y2y0. dx dx dy dx dy Practice: Find d x d √ d , (x2 y), and [y cos(xy)]. dx y dx dx MATH 162—Framework for Mon., Jan. 29 Review of Differentiation and Integration Integration The definite integral • the area problem • Riemann sums • definition Fundamental Theorem of Calculus: R x I: Suppose f is continuous on [a, b]. -
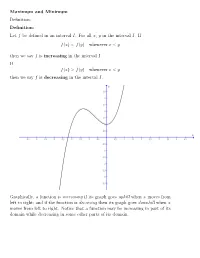
Maximum and Minimum Definition
Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing. -

A Collection of Problems in Differential Calculus
A Collection of Problems in Differential Calculus Problems Given At the Math 151 - Calculus I and Math 150 - Calculus I With Review Final Examinations Department of Mathematics, Simon Fraser University 2000 - 2010 Veselin Jungic · Petra Menz · Randall Pyke Department Of Mathematics Simon Fraser University c Draft date December 6, 2011 To my sons, my best teachers. - Veselin Jungic Contents Contents i Preface 1 Recommendations for Success in Mathematics 3 1 Limits and Continuity 11 1.1 Introduction . 11 1.2 Limits . 13 1.3 Continuity . 17 1.4 Miscellaneous . 18 2 Differentiation Rules 19 2.1 Introduction . 19 2.2 Derivatives . 20 2.3 Related Rates . 25 2.4 Tangent Lines and Implicit Differentiation . 28 3 Applications of Differentiation 31 3.1 Introduction . 31 3.2 Curve Sketching . 34 3.3 Optimization . 45 3.4 Mean Value Theorem . 50 3.5 Differential, Linear Approximation, Newton's Method . 51 i 3.6 Antiderivatives and Differential Equations . 55 3.7 Exponential Growth and Decay . 58 3.8 Miscellaneous . 61 4 Parametric Equations and Polar Coordinates 65 4.1 Introduction . 65 4.2 Parametric Curves . 67 4.3 Polar Coordinates . 73 4.4 Conic Sections . 77 5 True Or False and Multiple Choice Problems 81 6 Answers, Hints, Solutions 93 6.1 Limits . 93 6.2 Continuity . 96 6.3 Miscellaneous . 98 6.4 Derivatives . 98 6.5 Related Rates . 102 6.6 Tangent Lines and Implicit Differentiation . 105 6.7 Curve Sketching . 107 6.8 Optimization . 117 6.9 Mean Value Theorem . 125 6.10 Differential, Linear Approximation, Newton's Method . 126 6.11 Antiderivatives and Differential Equations . -

Second Derivative Math165: Business Calculus
Second Derivative Math165: Business Calculus Roy M. Lowman Spring 2010, Week6 Lec2 Roy M. Lowman Second Derivative second derivative definition of f0 Definition (first derivative) df f(x + ∆x) − f(x) = f0 = lim (1) dx ∆x−>0 ∆x ∆f = lim (2) ∆x−>0 ∆x ∆f ≈ average slope of f(x) over delta x, f0 (3) ∆x avg (4) Roy M. Lowman Second Derivative second derivative definition of f0 f0(x) is the slope of the function f(x) f0(x) is the rate of change of the function f(x) w.r.t x f0(x) is (+) where f(x) is increasing. f0(x) is (−) where f(x) is decreasing. f0(x) can be used to find intervals where f(x) is increasing/decreasing f0(x) = 0 or undefined where the sign of the slope can change, i.e. at CNs f0(x) = 0 at critical points The First Derivative Test can be used to determine what kind of critical points. f0(x) can tell you a lot about a function f(x) 0 ∆f 0 favg = ∆x can be used to extimate f (x) Roy M. Lowman Second Derivative second derivative definition of f0 f0(x) is the slope of the function f(x) f0(x) is the rate of change of the function f(x) w.r.t x f0(x) is (+) where f(x) is increasing. f0(x) is (−) where f(x) is decreasing. f0(x) can be used to find intervals where f(x) is increasing/decreasing f0(x) = 0 or undefined where the sign of the slope can change, i.e. -

AP Physics C 2017-2018 Welcome to the Most Rewarding and Challenging
AP Physics C 2017-2018 Welcome to the most rewarding and challenging course you will take during your high school career. You will be learning many valuable skills that will translate to numerous college majors and eventually your careers as well. The most important of which is how to think conceptually at a very high level. AP Physics C requires a large amount of time and energy. We will cover close to 25 chapters as we prepare for the 2 AP Physics C exams you can take in May. We will not take any days off. If you miss days, or arrive 10 minutes late each morning, you are in the wrong class. You are expected to complete a summer assignment that will help review some of the physics topics we will cover to begin the year. It will also introduce/review some of the calculus skills we will be incorporating. This is due The First Day of School!! It will be collected for a grade, and will be a significant portion of your 1st quarter grade. There will also be a quiz on the first day of school. Summer Assignment Due Wednesday August 16. 1. Complete the Introduction to Calculus Packet. Read the packet and solve any practice problems on notebook paper. 2. Read Chapter 1 in the textbook. Complete Problems #1, 5, 8, 10, 18, 23, 30, 35, 45 on notebook paper. 3. Read Chapter 2 in the textbook. Complete Questions #1, 5, 8 and Problems # 1, 5, 8, 15, 20, 27, 31, 37, 41, 45, 51, 58, 63, 67, 69, 70, 80, 92, 101 on notebook paper.