An Inverse Problem Approach to the Correction of Distortion in EPI Images Patrice Munger, Gerard R
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Loudspeaker FM and AM Distortion an 10
Loudspeaker FM and AM Distortion AN 10 Application Note to the KLIPPEL R&D SYSTEM The amplitude modulation of a high frequency tone f1 (voice tone) and a low frequency tone f2 (bass tone) is measured by using the 3D Distortion Measurement module (DIS) of the KLIPPEL R&D SYSTEM. The maximal variation of the envelope of the voice tone f1 is represented by the top and bottom value referred to the averaged envelope. The amplitude modulation distortion (AMD) is the ratio between the rms value of the variation referred to the averaged value and is comparable to the modulation distortion Ld2 and Ld3 of the IEC standard 60268 provided that the loudspeaker generates pure amplitude modulation of second- or third-order. The measurement of amplitude modulation distortion (AMD) allows assessment of the effects of Bl(x) and Le(x) nonlinearity and radiation distortion due to pure amplitude modulation without Doppler effect. CONTENTS: 1 Method of Measurement ............................................................................................................................... 2 2 Checklist for dominant modulation distortion ............................................................................................... 3 3 Using the 3D distortion measurement (DIS) .................................................................................................. 4 4 Setup parameters for DIS Module .................................................................................................................. 4 5 Example ......................................................................................................................................................... -

Statistical Distortion: Consequences of Data Cleaning
Statistical Distortion: Consequences of Data Cleaning Tamraparni Dasu Ji Meng Loh AT&T Labs Research AT&T Labs Research 180 Park Avenue 180 Park Avenue Florham Park, NJ 07932 Florham Park, NJ 07932 [email protected] [email protected] ABSTRACT There is considerable research in the database community We introduce the notion of statistical distortion as an essen- on varied aspects of data quality, data repair and data clean- tial metric for measuring the effectiveness of data cleaning ing. Recent work includes the use of machine learning for strategies. We use this metric to propose a widely applica- guiding database repair [14]; inferring and imputing miss- ble yet scalable experimental framework for evaluating data ing values in databases [10] ; resolving inconsistencies using cleaning strategies along three dimensions: glitch improve- functional dependencies [6]; and for data fusion [8]. ment, statistical distortion and cost-related criteria. Exist- From an enterprise perspective, data and information qual- ing metrics focus on glitch improvement and cost, but not ity assessment has been an active area of research as well. on the statistical impact of data cleaning strategies. We The paper [12] describes subjective and objective measures illustrate our framework on real world data, with a compre- for assessing the quality of a corporation’s data. An overview hensive suite of experiments and analyses. of well known data quality techniques and their comparative uses and benefits is provided in [2]. A DIMACS/CICCADA 1 workshop on data quality metrics featured a mix of speak- 1. INTRODUCTION ers from database and statistics communities. It covered a Measuring effectiveness of data cleaning strategies is al- wide array of topics from schema mapping, graphs, detailed most as difficult as devising cleaning strategies. -

En 300 720 V2.1.0 (2015-12)
Draft ETSI EN 300 720 V2.1.0 (2015-12) HARMONISED EUROPEAN STANDARD Ultra-High Frequency (UHF) on-board vessels communications systems and equipment; Harmonised Standard covering the essential requirements of article 3.2 of the Directive 2014/53/EU 2 Draft ETSI EN 300 720 V2.1.0 (2015-12) Reference REN/ERM-TG26-136 Keywords Harmonised Standard, maritime, radio, UHF ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice The present document can be downloaded from: http://www.etsi.org/standards-search The present document may be made available in electronic versions and/or in print. The content of any electronic and/or print versions of the present document shall not be modified without the prior written authorization of ETSI. In case of any existing or perceived difference in contents between such versions and/or in print, the only prevailing document is the print of the Portable Document Format (PDF) version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at http://portal.etsi.org/tb/status/status.asp If you find errors in the present document, please send your comment to one of the following services: https://portal.etsi.org/People/CommiteeSupportStaff.aspx Copyright Notification No part may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying and microfilm except as authorized by written permission of ETSI. -

DTV Interference Rejection Thresholds Are Shown on the Plot As a Reference
Interference Rejection Thresholds of Consumer Digital Television Receivers Available in 2005 and 2006 March 30, 2007 Technical Research Branch Laboratory Division Office of Engineering and Technology Federal Communications Commission OET Report Prepared by: FCC/OET 07-TR-1003 Stephen R. Martin ACKNOWLEDGEMENTS The author gratefully acknowledges the following contributions to this work. Mark Hryszko of the Digital Television group of Advanced Micro Devices provided the “Muddy Waters” RF vector file (mathematically derived from an MPEG2 transport stream) that was used with the Wavetech WS2100 RF player to provide a “desired signal” for the final few tests performed for this report. John Gabrysch of the Commission’s Media Bureau set up and evaluated the performance of the Rohde and Schwarz SFU DTV signal generator and developed channel assignment files for the instrument. The work of Charles Rhodes on third-order intermodulation inspired the paired-signal tests in this project. Gary Sgrignoli of MSW provided a fast-track DTV education to prepare the author for the prequel to this project. The author thanks the following Commission employees for reviewing drafts of this document: Alan Stillwell, Rashmi Doshi, and William Hurst (Office of Engineering and Technology); Doug Miller, John Raymond, and Steve DeSena (Enforcement Bureau); Richard Engelman and Sankar Persaud (International Bureau). The author also acknowledges the support of wife, Dr. Bonnie Dorr, through many long hours spent completing this work. i TABLE OF CONTENTS EXECUTIVE SUMMARY -

Spatial Characteristics of Distortion Radiated from Antenna Arrays with Transceiver Nonlinearities Christopher Mollen,´ Ulf Gustavsson, Thomas Eriksson, Erik G
1 Spatial Characteristics of Distortion Radiated from Antenna Arrays with Transceiver Nonlinearities Christopher Mollen,´ Ulf Gustavsson, Thomas Eriksson, Erik G. Larsson Abstract—The distortion from massive MIMO (multiple-input– paper is to give a rigorous description of the distortion created multiple-output) base stations with nonlinear amplifiers is studied by nonlinear hardware in multi-antenna transmitters, and to and its radiation pattern is derived. The distortion is analyzed quantify to which degree the distortion combines coherently. both in-band and out-of-band. By using an orthogonal Her- mite representation of the amplified signal, the spatial cross- The contribution of this paper is to give a rigorous correlation matrix of the nonlinear distortion is obtained. It continuous-time system model of a multi-antenna transmitter shows that, if the input signal to the amplifiers has a dominant for both single-carrier and OFDM (orthogonal frequency- beam, the distortion is beamformed in the same way as that beam. division multiplexing) transmission that uses digital precoding When there are multiple beams without any one being dominant, to beamform to multiple users. Orthogonal polynomials are it is shown that the distortion is practically isotropic. The derived theory is useful to predict how the nonlinear distortion will used to partition the amplified transmit signal into a desired behave, to analyze the out-of-band radiation, to do reciprocity signal—the linearly amplified signal—and a distortion term calibration, and to schedule users in the frequency plane to that is uncorrelated from the desired signal in order to analyze minimize the effect of in-band distortion. -

WAVEFORM TESTING Victor Nicholson CTIC the Urban Institute
WAVEFORM TESTING Victor Nicholson CTIC The Urban Institute Washington, DC have resulted in many complaints by broadcasters, of excessive degradation of their local channels when carried by a cable system. This is especially true of local UHF signals Abstract where interference is often introduced at the Existing subjective and frequency domain head end by the mixing of harmonics of the local testing procedures are shown to have major oscillator from the converter with other UHF. weaknesses in ensuring the delivery of accep Distribution system testing has little value in table television pictures to cable subscribers. resolving these complaints. Recommended, instead, are waveform test techniques using VIT signals as generated by Waveform test procedures have had little the networks. Applications of measurement application in the past to the cable industry as procedures and performance objectives are it was expensive to introduce these test signals discussed for echoes, noise and chrominance I at the head end. In addition, they provided no luminance gain and delay. information as to the quality of incoming tele ·,rision signals. Equipment was necessary to demodulate each channel, insert these diagnostic signals and then remodulate them; all of which added degradation to the desired TV signal. Today, waveform test procedures are applicable to the cable industry as these diagnostic signals are already injected into the Waveform testing of television signals four major network transmissions; ABC, CBS, introduces a valuable concept to the performance NBC, and PBS. This eliminates the need for testing and maintenance of R. F. distribution a cable operator to own expensive equipment to systems; including cable, satellite and fiber introduce these signals. -

Nonlinear Distortion Identification Based on Intra-Wave Frequency
Appl. Math. Inf. Sci. 6, No. 3, 689-695 (2012) 689 Applied Mathematics & Information Sciences An International Journal ⃝c 2012 NSP Natural Sciences Publishing Cor. Nonlinear Distortion Identification based on Intra-wave Frequency Modulation Yutian Wang1, Hui Wang1 and Qin Zhang1 Information Engineering School, Communication University of China, Beijing 100024, China Received: Apr. 8, 2012; Revised May 4, 2012; Accepted May 26, 2012 Published online: 1 September 2012 Abstract: Recently, most of the methods used to measure and analysis signal property are based on the linear transform theory, such as FFT, STFT, wavelet, etc. Unfortunately, these methods usually cause meaningless results when it is used to analysis nonlinear signal. In this paper, we use Hilbert-Huang transform (HHT) to review the nonlinear distortion and define a novel nonlinear parameter named Nonlinear Distortion Degree (NDD) which is based on intra-wave frequency modulation measurement. The loudspeaker model simulations are used to illustrate the intra-wave frequency modulation caused by nonlinear distortion. The results agree that NDD can reveal more accurate and physical meaningful nonlinear distortion characteristic. Keywords: Nonlinear distortion, HHT, intra-wave frequency modulation, loudspeaker. 1. Introduction Huang et. al. raised a novel signal processing method named Hilbert-Huang Transform (HHT) based on EMD (Empirical Mode Decomposition), which is suitable for In the signal analysis field, Fourier based analysis meth- analyzing nonlinear and non-stationary signal [2]. Differ- ods such as FFT and STFT take the dominated position. ent from the traditional signal processing methods, the H- However, there are some crucial restrictions of the Fourier HT is an adaptive decomposition method and can yield spectral analysis: the system must be linear and the data more physical results. -

On Nicam Datacasting
ON NICAM DATACASTING Cristian Ciressan, Lucian Prodan EPFL CH-1015 Ecublens, Suisse Emails: [email protected]fl.ch, prodan@epfl.ch Abstract Data transmission technologies changes rapidly these days due to increased re- quirements in bandwidth and reliability. NICAM standard (which stands for Near Instantaneous Companded Audio Multiplex ) was designed to be a digital audio transmission standard and later it was used by the BBC to convey digital stereo sound for TV. It was obvious that allowing data transmission would be, if not a must, at least a welcome feature and in consequence it was extended to allow raw data or mixed data and sound to be transmitted. NICAM is feasible for terrestrial, cable, microwave links and satellites. This paper introduces some basic notions about NICAM datacasting and presents the results of a project whose aim was to design two PC-cards that allow unidirectional data transmission using the NICAM standard. Keywords: NICAM 728, subcarrier, QPSK 1. Introduction NICAM (or to give it its full name, NICAM 728) was invented during the early 1980’s by the BBC Research Center, Kingswood Warren. It was first applied to the British ”System I” 625 line PAL colour TV broadcasting system, and premiered in 1986 on the ”First Night of the Proms” concert program. Since that time it has been slightly modified by the Nordic broadcasters to work with the more common “System B/G” used over much of continental Europe. It has been demonstrated to work also with “System D/K” used in some countries of eastern Europe , and with “System L” used in France. -

Options of Enhanced Secam Tv Transmission System
Gofaizen O.V. (UKRAINE, UNIIRT) OPTIONS OF ENHANCED SECAM TV TRANSMISSION SYSTEM Introduction The questions of transition from analogue to digital TV in countries, using analogue TV SECAM transmission system are discussed in this report with consideration of its enhancement in accor- dance with conception of EQTV systems. The transition period is characterized with that in its beginning infrastructure and park of TV sets are analogue. At the beginning of transition period TV broadcasting is mainly analogue, and a number of digital TV sets is minimal, and apparently for a long time analogue and digital TV will co-exist. Simultaneously with implementation of digital TV analogue TV has to be supported and enhanced [1]. The issues of compatibility of new digital and old analogue TV are extremely important, and here the main consideration is attended to them. 1 The position of analogue enhanced quality television in the period of transition to digi- tal television We have to take into consideration that the main event of the present in television is the transition to digital TV. Nevertheless, this transition may continue in some countries for long time enough. All this depends on many factors – relationship between the cost of digital sets (tuners, set top boxes) and of analog ones, real term for change from analog to digital infrastructure and the affordablence of this change, purchasing power of viewers community, presence and condition of used equipment. It is quite possible, that in some coun- tries this transition would come in a quite short time, in others this transition would continue for decades. -

Correction of the Distortion in Frequency-Modulation Spectroscopy Frédéric Du Burck, Olivier Lopez
Correction of the distortion in frequency-modulation spectroscopy Frédéric Du Burck, Olivier Lopez To cite this version: Frédéric Du Burck, Olivier Lopez. Correction of the distortion in frequency-modulation spectroscopy. Measurement Science and Technology, IOP Publishing, 2004, 15, pp.1327-1336. hal-00003179 HAL Id: hal-00003179 https://hal.archives-ouvertes.fr/hal-00003179 Submitted on 26 Oct 2004 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Correction of the distortion in frequency modulation spectroscopy F. du Burck, O. Lopez Laboratoire de Physique des Lasers – Université Paris 13 Avenue Jean-Baptiste Clément, 93430, Villetaneuse, France. Abstract A theoretical expression of the detected signal in frequency modulation spectroscopy with a residual amplitude modulation (RAM) is computed. The line shape distortion induced by the RAM is shown to be essentially suppressed for a proper choice of the modulation and detection parameters. The experimental tests are carried out in saturation spectroscopy of I2 at 514.5 nm. Experimental limitations are analysed. Key words Frequency modulation (FM) spectroscopy, residual amplitude modulation (RAM), line shape, laser spectroscopy, ultra-high resolution spectroscopy I. Introduction The technique of frequency modulation (FM) spectroscopy was proposed by Bjorklund for the study of weak absorptions and dispersions with a dye laser [1,2] and independently by Drever and Hall for sub-Doppler spectroscopy and for the detection of the reflected field by a Fabry-Perot resonator for laser stabilization [3,4,5]. -
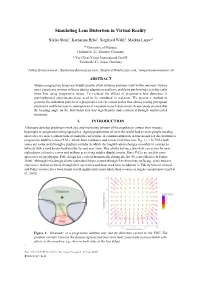
Simulating Lens Distortion in Virtual Reality
Simulating Lens Distortion in Virtual Reality Niklas Stein1, Katharina Rifai2, Siegfried Wahl3, Markus Lappe4 1,4 University of Münster, Fliednerstr. 21, Münster, Germany 2,3Carl Zeiss Vision International GmbH, Turnstraße 27, Aalen, Germany [email protected], [email protected], [email protected], [email protected] ABSTRACT Modern progressive lenses are widely used to allow distance and near-view within one lens. Novice users experience motion sickness during adaptation and have problems performing everyday tasks when first using progressive lenses. To evaluate the effects of progressive lens distortion in psychophysical experiments these need to be simulated in real-time. We present a method to generate the distortion pattern of a progressive lens in virtual reality that allows testing perceptual distortions and behavioural consequences of exposure to such distortions. A user study showed that the heading angle on the horizontal axis was significantly underestimated through implemented distortion. 1. INTRODUCTION All people develop presbyopia with age, and increasing amount of the population correct their myopia, hyperopia or astigmatism using spectacles. Ageing populations all over the world lead to more people needing spectacles to correct conjunctions of multiple corrections. A common approach in lens design for this problem is progressive additive lenses (PAL), which have a distance and a near view zone (see Fig. 1). ). In PALs both zones are connected through a gradient corridor in which the magnification changes smoothly in contrast to bifocals with a hard border between the far and near zone. This allows having a lens with correction for near sightedness, refractive errors and without perceiving sudden displacements. -

Diplexer Filter, BK-26N All Standard DAS Services/Wimax/W-LAN 802.11(A) 80 - 2690 / 3300 - 5850 Mhz Rev
Diplexer Filter, BK-26N All standard DAS Services/WiMax/W-LAN 802.11(a) 80 - 2690 / 3300 - 5850 MHz Rev. C t Combines 5 GHz W-LAN & WiMax to other DAS services t Meets European Rail Standards EN50155: 2001 t 50 dB Input Isolation t 50 W Through Power t Low Passive IM., PIM t Minimal RF Insertion Loss t Rugged, High Reliability Design t N connectors standard BK-26N 3 GHz Diplexer allows efficient com- Passband J1 to J3: 3,300 to above 5,850 MHz Passband J2 to J3: below 80 to 2,690 MHz bining of WiMAX and 5 GHz W-LAN designed to J1 to J2 Isolation: >50dB in band except near cross over 802.11(a) and similar systems, with a coaxial dis- >47dB 2680-2690 & 3300-3330 MHz tributed in-building cellular network or DAS. The unit Return Loss: >18 dB, all ports has an extremely broad frequency range with mini- Passband Loss: 0.2 dB typ., 0.8 dB max. J2-J3 Power Rating: 50W avg. max., DC of <1A mal loss for maximum flexibility. This can provide J1-J3 Power Rating: 5W avg. max., no DC path the benefit of the same controlled coverage of the Impedance: 50W nominal higher frequency services with the DAS. Intermod. Distortion: <-150 dBc (test with 2 x +43 dBm tones) The Diplexer has been designed to be small and Environment: -40° - +80°C, IP64 (IP67 to order) lightweight, using passive, proprietary techniques to Applications: Indoor ensure minimal loss and very high reliability. A sim- Finish: N Connectors: Triplate ple bracket and tapped holes are provided for simple Housing: RoHS conversion process Weight, nominal: 13.2 oz (370 g) mounting to a surface or cable tray.