Spatial Modeling of Oligonychus Perseae (Tuttle, Baker and Abbatiello) Using Geostatistical Techniques
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Catalogos a Nivel Entidad, Distrito Local, Municipio Y Seccion
DIRECCIÓN EJECUTIVA DEL REGISTRO FEDERAL DE ELECTORES CATALOGOS A NIVEL ENTIDAD, DISTRITO LOCAL, MUNICIPIO Y SECCION ENTIDAD NOMBRE_ENTIDAD DISTRITO_LOCAL MUNICIPIO NOMBRE_MUNICIPIO SECCION 15 MEXICO 1 107 TOLUCA 5207 15 MEXICO 1 107 TOLUCA 5208 15 MEXICO 1 107 TOLUCA 5209 15 MEXICO 1 107 TOLUCA 5210 15 MEXICO 1 107 TOLUCA 5211 15 MEXICO 1 107 TOLUCA 5212 15 MEXICO 1 107 TOLUCA 5213 15 MEXICO 1 107 TOLUCA 5214 15 MEXICO 1 107 TOLUCA 5215 15 MEXICO 1 107 TOLUCA 5216 15 MEXICO 1 107 TOLUCA 5217 15 MEXICO 1 107 TOLUCA 5218 15 MEXICO 1 107 TOLUCA 5219 15 MEXICO 1 107 TOLUCA 5220 15 MEXICO 1 107 TOLUCA 5221 15 MEXICO 1 107 TOLUCA 5222 15 MEXICO 1 107 TOLUCA 5223 15 MEXICO 1 107 TOLUCA 5224 15 MEXICO 1 107 TOLUCA 5225 15 MEXICO 1 107 TOLUCA 5226 15 MEXICO 1 107 TOLUCA 5227 15 MEXICO 1 107 TOLUCA 5228 15 MEXICO 1 107 TOLUCA 5229 15 MEXICO 1 107 TOLUCA 5230 15 MEXICO 1 107 TOLUCA 5231 15 MEXICO 1 107 TOLUCA 5232 15 MEXICO 1 107 TOLUCA 5233 15 MEXICO 1 107 TOLUCA 5234 15 MEXICO 1 107 TOLUCA 5235 15 MEXICO 1 107 TOLUCA 5236 15 MEXICO 1 107 TOLUCA 5237 15 MEXICO 1 107 TOLUCA 5238 1 DIRECCIÓN EJECUTIVA DEL REGISTRO FEDERAL DE ELECTORES CATALOGOS A NIVEL ENTIDAD, DISTRITO LOCAL, MUNICIPIO Y SECCION ENTIDAD NOMBRE_ENTIDAD DISTRITO_LOCAL MUNICIPIO NOMBRE_MUNICIPIO SECCION 15 MEXICO 1 107 TOLUCA 5239 15 MEXICO 1 107 TOLUCA 5240 15 MEXICO 1 107 TOLUCA 5241 15 MEXICO 1 107 TOLUCA 5242 15 MEXICO 1 107 TOLUCA 5243 15 MEXICO 1 107 TOLUCA 5244 15 MEXICO 1 107 TOLUCA 5245 15 MEXICO 1 107 TOLUCA 5246 15 MEXICO 1 107 TOLUCA 5247 15 MEXICO 1 107 TOLUCA 5248 15 -

Derechos De La Familia Derechos De Los Niños Y Las Niñas Derechos De La Mujer Eventos Relevantes
PROFAMIN 27 cómo cada uno de los miembros DERECHOS DE actúa a la defensiva, reforzando la DERECHOS DE LA FAMILIA adhesión a las creencias y LA MUJER presupuestos que alimenta el mito Fechas: 09, 10, 14, 15, 16, 17, familiar y configuran las reglas a Fechas: 15, 21, 22, 23, 25, 28 y 21, 22, 23, 25, 29 y 30 de enero, menudo tremendamente estrictas 30 de enero, así como 06, 11, 12, así como 01, 04, 06, 07, 08, 11, que rigen el funcionamiento de 13, 14, 15, 19, 20, 21, 22, 25 y 12, 13, 14, 15, 18, 19, 21, 22, estas familias. 27 de febrero. 25, 27 y 28 de febrero. Por ello, resulta indispensable Lugares: Calimaya, Villa de Lugares: Ocoyoacac, Toluca, concienciar a los integrantes del Allende, Nezahualcóyotl, Coatepec Rayón, Calimaya, Villa de Allende, núcleo familiar a efecto de Harinas, Rayón, Toluca, Metepec, Nezahualcóyotl, Coatepec Harinas, modificar el status que predomina Ocoyoacac, Zacualpan, San Metepec, San Mateo Atenco, y favorecer el desarrollo familiar. Mateo Atenco, Otzolotepec, San Rayón, Zacualpan, Ocoyoacac, Antonio la Isla, Tejupilco, Otzolotepec, San Antonio la Isla, Mexicaltzingo, Temoaya, Acambay, Tejupilco, Mexicaltzingo, Temoaya, DERECHOS DE Teotihuacán, San José del Rincón Acambay, Tejupilco, Teotihuacán, y Valle de Bravo. San José del Rincón y Valle de LOS NIÑOS Y Bravo. LAS NIÑAS Asistentes: 2,591 personas. Asistentes: 3,289 personas. Fechas: 09, 10, 11, 14, 15, 16, En México, como en muchas otras 17, 21, 22, 23, 25, 28, 29 y 30 de partes del mundo, la mujer padece Si bien las familias pasan algún enero, así como 01, 04, 05, 06, en nuestros días, vejaciones que momento difícil durante la 07, 08, 11, 12, 14, 15, 18, 19, vulneran su dignidad humana, las convivencia cotidiana, algunas 20, 21, 25, 27 y 28 de febrero. -

Geology of Nevado De Toluca Volcano and Surrounding Areas, Central Mexico
mch089 1 of 26 Geological Society of America Map and Chart Series MCH089 2002 Geology of Nevado de Toluca Volcano and surrounding areas, central Mexico *Armando García-Palomo, José Luis Macías, José Luis Arce Instituto de Geofísica, Universidad Nacional Autónoma de México, Coyoacán 04510, México D.F., México Lucia Capra Instituto de Geografía, Universidad Nacional Autónoma de México, Coyoacán 04510, México D.F., México Victor Hugo Garduño Departamento de Geología y Mineralogía, Instituto de Investigaciones Metalúrgicas, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, Michoacán, México Juan Manuel Espíndola Instituto de Geofísica, Universidad Nacional Autónoma de México, Coyoacán 04510, México D.F., México ABSTRACT Nevado de Toluca is an andesitic-dacitic stratovolcano of Pliocene-Holocene age located in central Mexico. The volcano is built on a complex sequence of metamorphic and sedimentary formations of Jurassic-Cretaceous age, rhyolitic ignimbrites of late Eocene age, and massive andesitic lava flows of late Miocene. In the northwest corner of the map area, on top of this basement sequence, a complex andesitic-dacitic strato- volcano, San Antonio, and a series of andesitic-dacitic domes and cones of Pliocene– early Pleistocene age were also built. The first andesitic-dacitic emissions of Nevado de Toluca occurred 2.6 Ma and continued during late Pleistocene–Holocene time contem- porarily with basaltic to dacitic emissions of the Chichinautzin Volcanic Field in the eastern parts of the map area. Volcanism in the area has been controlled by the interplay of three fault systems active since late Miocene. These systems, from older to younger, are the Taxco-Querétaro Fault System (NNW–SSE), the San Antonio Fault System (NE–SW), and the Tenango Fault System (E–W). -

MÉXICO* Municipios Entidad Tipo De Ente Público Nombre Del Ente Público
Inventario de Entes Públicos MÉXICO* Municipios Entidad Tipo de Ente Público Nombre del Ente Público México Municipio 15-001 Acambay México Municipio 15-002 Acolman México Municipio 15-003 Aculco México Municipio 15-004 Almoloya de Alquisiras México Municipio 15-005 Almoloya de Juárez México Municipio 15-006 Almoloya del Río México Municipio 15-007 Amanalco México Municipio 15-008 Amatepec México Municipio 15-009 Amecameca México Municipio 15-010 Apaxco México Municipio 15-011 Atenco México Municipio 15-012 Atizapán México Municipio 15-013 Atizapán de Zaragoza * Inventario elaborado con información del CACEF y EFSL. 19 de marzo de 2020 Inventario de Entes Públicos MéxicoMÉXICO* Municipio 15-014 Atlacomulco México Municipio 15-015 Atlautla México Municipio 15-016 Axapusco México Municipio 15-017 Ayapango México Municipio 15-018 Calimaya México Municipio 15-019 Capulhuac México Municipio 15-020 Coacalco de Berriozábal México Municipio 15-021 Coatepec Harinas México Municipio 15-022 Cocotitlán México Municipio 15-023 Coyotepec México Municipio 15-024 Cuautitlán México Municipio 15-025 Chalco México Municipio 15-026 Chapa de Mota México Municipio 15-027 Chapultepec México Municipio 15-028 Chiautla México Municipio 15-029 Chicoloapan Inventario de Entes Públicos MéxicoMÉXICO* Municipio 15-030 Chiconcuac México Municipio 15-031 Chimalhuacán México Municipio 15-032 Donato Guerra México Municipio 15-033 Ecatepec de Morelos México Municipio 15-034 Ecatzingo México Municipio 15-035 Huehuetoca México Municipio 15-036 Hueypoxtla México Municipio -

H. Consejo Directivo Xlviii Sesión Ordinaria
H. CONSEJO DIRECTIVO XLVIII SESIÓN ORDINARIA H. CONSEJO DIRECTIVO UNIVERSIDAD MEXIQUENSE DEL BICENTENARIO XLVIII SESIÓN ORDINARIA INFORME DE ACTIVIDADES FEBRERO – MARZO 2018 Con fundamento en lo dispuesto en el Reglamento de la Ley para la Coordinación y el Control de los Organismos Auxiliares y Fideicomisos del Estado de México y el Decreto de Creación de la Universidad Mexiquense del Bicentenario, se presenta ante este H. Consejo Directivo el “Informe de Actividades de la Rectora Suplente, correspondiente al período Febrero – Marzo 2018”. I. ASPECTOS ACADÉMICOS PROCESO DE ADMISIÓN La UMB se encuentra en proceso de admisión al Ciclo Escolar 2018 – 2019 para ello se han registrado 2,888 aspirantes en la plataforma del SIDIUMB, de los cuales 1,303 han realizado el pago correspondiente y se han confirmado en el sistema mencionado; la distribución por UES es la siguiente: N.P. UES Registrados Confirmados 28 Tultepec 536 247 23 Ecatepec 251 100 24 Ixtapaluca 245 88 20 Tultitlán 218 59 11 Lerma 184 102 27 El Oro 187 103 9 Jilotepec 159 98 17 Temoaya 124 81 18 Tenango del Valle 82 50 21 Villa Victoria 84 46 6 Atenco 73 27 4 Chalco 62 26 29 Villa del Carbón 98 51 8 Ixtlahuaca 58 26 25 Tepotzotlán 56 18 15 Tecámac 53 13 16 Tejupilco 51 27 5 Coatepec Harinas 48 0 10 Jiquipilco 48 26 22 Xalatlaco 48 27 7 Huixquilucan 40 11 6 La Paz 35 7 19 Tlatlaya 34 19 Página | 1 1 Acambay 30 14 26 Temascalcingo 20 9 50 UESAME 19 10 14 Sultepec 13 5 13 San José del Rincón 12 4 Almoloya de 2 11 3 Alquisiras 12 Morelos 9 6 TOTAL 2,888 1,303 CAPACITACIÓN DOCENTE Con el propósito de fortalecer el proceso enseñanza-aprendizaje en las Unidades de Estudios Superiores que conforman la Universidad, se llevó a cabo el Programa de Capacitación Docente, el cual se aplica en cada periodo inter-semestral; durante dos semanas se impartieron 11 cursos con diferentes temáticas, cuyo objetivo es mejorar las habilidades docentes. -

Xliii Sesión Ordinaria Del H
XLIII SESIÓN ORDINARIA DEL H. CONSEJO DIRECTIVO CONSEJO DIRECTIVO UNIVERSIDAD MEXIQUENSE DEL BICENTENARIO XLIII SESIÓN ORDINARIA INFORME DE ACTIVIDADES ABRIL 05 – JUNIO 05 DE 2017 Con fundamento en lo dispuesto por el artículo 11, fracción XI del Decreto del Ejecutivo del Estado por el que se crea la Universidad Mexiquense del Bicentenario, así como lo previsto en el artículo 19, fracción VII del Reglamento de la Ley para la Coordinación y el Control de los Organismos Auxiliares y Fideicomisos del Estado de México, se presenta ante este H. Consejo Directivo el “Informe de Actividades del Rector de la Universidad Mexiquense del Bicentenario, correspondiente al período del 05 de abril al 05 de junio de 2017”. I. ASPECTOS ACADÉMICOS MATRÍCULA ACTUAL La comunidad estudiantil de la Universidad se encuentra conformada por 10,520 estudiantes distribuidos en 92 opciones educativas que se imparten en 30 Unidades de Estudios Superiores. UES Matrícula UES Matrícula Acambay 245 Sultepec 178 Almoloya de Alquisiras 91 Tecámac 273 Atenco 351 Tejupilco 207 Chalco 317 Temascalcingo 60 Coatepec Harinas 231 Temoaya 310 Ecatepec 597 Tenango del Valle 407 El Oro 526 Tepotzotlán 235 Huixquilucan 352 Tlatlaya 340 Ixtapaluca 1,124 Tultepec 667 Ixtlahuaca 394 Tultitlán 576 Jilotepec 852 Villa del Carbón 235 Jiquipilco 206 Villa Victoria 464 La Paz 270 Xalatlaco 123 Lerma 608 Adultos Mayores 70 Morelos 92 Total 10,520 San José del Rincón 119 Página 1 de 14 PROCESO DE INGRESO 2017 – 2018 Como parte de la primera convocatoria de ingreso para el ciclo escolar 2017 – 2018, se llevó a cabo la aplicación del examen de admisión a 3,314 aspirantes en las 29 Unidades de Estudios Superiores, para las que aplica la convocatoria. -
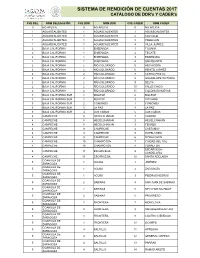
Anexo 10. DDR CADER
SISTEMA DE RENDICIÓN DE CUENTAS 2017 CATÁLOGO DE DDR's Y CADER's CVE DEL NOM DELEGACIÓN CVE DDR NOM DDR CVE CADER NOM CADER 0 NO APLICA 0 NO APLICA 0 NO APLICA 1 AGUASCALIENTES 1 AGUASCALIENTES 1 AGUASCALIENTES 1 AGUASCALIENTES 1 AGUASCALIENTES 2 CALVILLO 1 AGUASCALIENTES 1 AGUASCALIENTES 3 PABELLON 1 AGUASCALIENTES 1 AGUASCALIENTES 4 VILLA JUÁREZ 2 BAJA CALIFORNIA 1 ENSENADA 1 TIJUANA 2 BAJA CALIFORNIA 1 ENSENADA 2 TECATE 2 BAJA CALIFORNIA 1 ENSENADA 3 ENSENADA 2 BAJA CALIFORNIA 1 ENSENADA 4 SAN QUINTÍN 2 BAJA CALIFORNIA 2 RÍO COLORADO 5 HECHICERA 2 BAJA CALIFORNIA 2 RÍO COLORADO 6 BENITO JUÁREZ 2 BAJA CALIFORNIA 2 RÍO COLORADO 7 CERRO PRIETO 2 BAJA CALIFORNIA 2 RÍO COLORADO 8 GUADALUPE VICTORIA 2 BAJA CALIFORNIA 2 RÍO COLORADO 9 DELTA 2 BAJA CALIFORNIA 2 RÍO COLORADO 10 VALLE CHICO 2 BAJA CALIFORNIA 2 RÍO COLORADO 11 COLONIAS NUEVAS 3 BAJA CALIFORNIA SUR 1 MULEGÉ 2 MULEGE 3 BAJA CALIFORNIA SUR 1 MULEGÉ 3 VIZCAINO 3 BAJA CALIFORNIA SUR 2 COMONDÚ 1 COMONDÚ 3 BAJA CALIFORNIA SUR 3 LA PAZ 4 LA PAZ 3 BAJA CALIFORNIA SUR 4 LOS CABOS 5 LOS CABOS 4 CAMPECHE 8 HECELCHAKAN 1 CALKINI 4 CAMPECHE 8 HECELCHAKAN 2 HECELCHAKAN 4 CAMPECHE 8 HECELCHAKAN 3 TENABO 4 CAMPECHE 9 CAMPECHE 4 CASTAMAY 4 CAMPECHE 9 CAMPECHE 5 HOPELCHEN 4 CAMPECHE 9 CAMPECHE 6 DZIBALCHEN 4 CAMPECHE 10 CHAMPOTON 7 CIUDAD DEL SOL 4 CAMPECHE 10 CHAMPOTON 8 YOHALTUN ESCÁRCEGA- 4 CAMPECHE 11 ESCÁRCEGA 9 CANDELARIA 4 CAMPECHE 11 ESCÁRCEGA 10 SANTA ADELAIDA COAHUILA DE 5 1 ACUÑA 1 JIMÉNEZ ZARAGOZA COAHUILA DE 5 1 ACUÑA 2 ZARAGOZA ZARAGOZA COAHUILA DE 5 1 ACUÑA 3 PIEDRAS NEGRAS ZARAGOZA -

Toluca Tenango Del Valle Pb2001001 Ejido San Pedro Tlanixco Aurelia Gonzalez Mireles 7.50 15,000.00 Toluca Almoloya De Juarez Pb
LISTADO DE BENEFICIARIOS PRIMERA ASIGNACIÓN DIRECCIÓN DE RESTAURACIÓN Y FOMENTO FORESTAL DEPARTAMENTO DE REFORESTACIÓN REFORESTANDO EDOMÉX 2020 CATEGORÍA "REFORESTACIÓN" DELEGACIÓN REGIONAL SUPERFICIE MUNICIPIO No. FOLIO NOMBRE DEL PREDIO NOMBRE (S) DEL REPRESENTANTE MONTO ($) FORESTAL APROBADA (ha) TOLUCA TENANGO DEL VALLE PB2001001 EJIDO SAN PEDRO TLANIXCO AURELIA GONZALEZ MIRELES 7.50 15,000.00 TOLUCA ALMOLOYA DE JUAREZ PB2001002 EJIDO SAN AGUSTIN POTEJE JOSE ESTRADA ARRIAGA 4.00 8,000.00 TOLUCA TIANGUISTENCO PB2001003 BIENES COMUNALES DE SANTIAGO TILAPA ROGELIO CORMONA DIAZ 15.00 30,000.00 TOLUCA TIANGUISTENCO PB2001004 LA PILA ALFREDO GONZALEZ LOYA 1.20 2,400.00 TOLUCA XONACATLAN PB2001005 EL CANDELERO ALBINO ALMEIDA GARCIA 1.00 2,000.00 PARCELA 1094 Z1 P1/1, EJ. PRESA DE TOLUCA ALMOLOYA DE JUAREZ PB2001007 MARCOS GOMORA REYES 1.00 2,000.00 ARROYO ZARCO TOLUCA TIANGUISTENCO PB2001008 TERRENO DE LABOR EN COAXCATONCO JUAN YAÑEZ GARCIA 1.00 2,000.00 BIENES COMUNALES DE CALIMAYA DE DIAZ BONIFACIO MIGUEL GONZALEZ TOLUCA CALIMAYA PB2001010 69.80 139,600.00 GONZALEZ GOMORA BIENES COMUNALES DE SAN PEDRO TOLUCA TENANGO DEL VALLE PB2001011 MARIO ARELLANO GARCIA 10.00 20,000.00 ZICTEPEC BIENES COMUNALES DE SANTIAGO LEOVIGILDO VIRGILIO TOLUCA TOLUCA PB2001015 35.00 70,000.00 TLACOTEPEC ALARCON CLAVEL CIRO ENRIQUE ESTRADA TOLUCA ALMOLOYA DE JUAREZ PB2001016 INNOMINADO 1.30 2,600.00 ARRIAGA TOLUCA ZINACANTEPEC PB2001017 EJIDO EL CONTADERO AMADO REYES ELIZALDE 27.21 54,420.00 TOLUCA LERMA PB2001021 EJIDO SANTA MARIA TLALMIMILOLPAN ANTONIO MENDOZA ALVAREZ 4.92 9,840.00 JESUS ESTEBAN SERRANO TOLUCA XALATLACO PB2001024 ARRIBA DEL CODO 1.00 2,000.00 YAÑEZ BIENES COMUNALES SAN LORENZO TOLUCA LERMA PB2001028 GERARDO GONZALEZ ORTEGA 22.50 45,000.00 HUITZIZILAPAN PARCELA 347 Z1 P1, EJIDO PRESA DE GUILLERMINA CARBAJAL TOLUCA ALMOLOYA DE JUAREZ PB2001030 2.00 4,000.00 ARROYO ZARCO ZEPEDA TERRENO DE USO COMUN, B. -

Año 2, Esp. 16
GACETA MUNICIPAL DE GOBIERNO Publicación Oficial del H.Ayuntamiento de Nezahualcóyotl 2019-2021 • 2019 - 2021 • 29 de mayo de 2020 • Año 2 Especial 16 AÑO 2, ESPECIAL 16 Nezahualcóyotl, Estado de México; Viernes 29 de mayo de 2020 NEZA CIUDAD DE TODOS 1 GACETA MUNICIPAL DE GOBIERNO ACUERDO POR EL QUE SE PROHIBE LA VENTA DE BEBIDAS ALCOHÓLICAS EN TODAS SUS GRADUACIONES Y MODALIDADES EN LOS ESTABLECIMIENTOS MERCANTILES UBICADOS EN EL MUNICIPIO DE NEZAHUALCOYOTL, ESTADO DE MÉXICO DURANTE LA EMERGENCIA SANITARIA SARS-COV2 (COVID-19), POR EL PERÍODO COMPRENDIDO DEL TREINTA Y UNO DE MAYO DE DOS MIL VEINTE Y HASTA QUE LAS AUTORIDADES SANITARIAS CORRESPONDIENTES DETERMINEN LA REANUDACIÓN DE LAS ACTIVIDADES ECONÓMICAS, GARANTIZANDO, EN TODO MOMENTO, LAS MEDIDAS DE PREVENCIÓN E HIGIENE CORRESPONDIENTES DE CONFORMIDAD AL SISTEMA DE SEMÁFOROS ESTABLECIDO POR LA SECRETARÍA DE SALUD DEL GOBIERNO FEDERAL Y; C O N S I D E R A N D O Que el artículo 4o. de la Constitución Política de los Estados Unidos Mexicanos establece que toda persona tiene derecho a la protección de la salud, por lo que todas las autoridades en el ámbito de sus competencias, tienen la obligación de garantizar y establecer los mecanismos necesarios para que toda persona goce de un estado de completo bienestar físico, mental y social para su desarrollo. Que con fecha 19 de marzo de 2020, este H. Ayuntamiento tuvo a bien aprobar el Acuerdo numero 151 POR EL QUE SE APROBÓ Y AUTORIZO ESTABLECER MEDIDAS DE PREVENCIÓN DE RIESGOS ANTE LA CONTINGENCIA SANITARIA DEL CORONAVIRUS (COVID-19), EN PRO DE LA SALUD Y BIENESTAR DE LA POBLACIÓN DEL MUNICIPIO DE NEZAHUALCÓYOTL. -

C O N T E N I D O
Año: 02 No. 56 29 de mayo de 2020 H. Ayuntamiento de Metepec 2019-2021 C O N T E N I D O • ACUERDO DE LA PRESIDENTA MUNICIPAL CONSTITUCIONAL DE METEPEC, ESTADO DE MÉXICO, POR EL QUE SE MODIFICA LA SUSPENSIÓN DE PLAZOS Y TÉRMINOS LEGALES EN LA ADMINISTRACIÓN PÚBLICA MUNICIPAL DE METEPEC EN COORDINACIÓN CON LOS ÓRGANOS DESCENTRALIZADOS, Y LA QUE SE REFIERE EL DIVERSO ACUERDO PUBLICADO EL 17 DE ABRIL DE 2020, DEBIDO A LA EMERGENCIA SANITARIA POR CAUSA DE FUERZA MAYOR OCASIONADA POR EL CORONAVIRUS (COVID)19. 29 de mayo de 2020 Oficio: MET/PM/185/2020 CC. DIRECTORES, SUBDIRECTORES, JEFES DE DEPARTAMENTO, JEFES DE ÁREA, PERSONAL EN GENERAL DE LA ADMINISTRACIÓN PÚBLICA MUNICIPAL Y A LA POBLACIÓN EN GENERAL DE METEPEC, ESTADO DE MÉXICO P R E S E N T E Gabriela Gamboa Sánchez, Presidenta Constitucional de Metepec, con fundamento en lo dispuesto por los artículos 4 y 115 de la Constitución Política de los Estados Unidos Mexicanos; 113, 122, 123 y 125 de la Constitución Política del Estado Libre y Soberano de México; 3, 27, 29, 30, y las fracciones I y XXXIX del artículo 31, fracciones II y XVII del artículo 48 de la Ley Orgánica Municipal del Estado de México; 12, 24, 27, 28 y demás relativos y aplicables del Bando Municipal de Metepec, Estado de México 2020; y 1.3., 2.1, 2.2, 2.3, 2.14, 2.16, 2.18, 2.45, 3.7. y demás relativos y aplicables del Código de Reglamentación Municipal de Metepec, Estado de México; así como lo relativo en el segundo transitorio del acuerdo número 063/2020, publicado en la Gaceta Municipal, Año: 02, No. -

A Study of Avocado Germplasm Resources, 1988-1990. II. Findings from the Central Part of Mexico
Proc. of Second World Avocado Congress 1992 pp. 543-544 A Study of Avocado Germplasm Resources, 1988-1990. II. Findings from the Central Part of Mexico A. Ben-Ya'acov Ministry of Agriculture, Agricultural Research Organization Bet Dagan, P.O. Box 6, 50- 150, Israel L. López López, Eulogio De La Cruz Torres, and Alejandro F. Barrientos Priego CICTAMEX, Palacio Municipal, Coatepec Harinas, Mexico, C.P. 51700, Mexico Abstract. Several explorations were made in the central area of Mexico, including the states of México, Puebla, Querétaro, Morelos and Guanajuato, with the aim to locate specimens of avocado (Persea americana Mill.) and related species of the genus Persea with outstanding characteristics of vegetative growth, pest and disease resistance, adaptation to unfavorable environmental conditions, good fruit quality and phylogenetic importance for selection and breeding purposes. The current status of this research is presented. Mexico is a center of origin and dispersal of avocado (Popenoe, 1935; Smith, 1966). Within its borders is a great diversity of types, which constitutes a valuable germplasm resource that must be explored, collected, preserved and evaluated. The great avocado genetic diversity in Mexico, resulting from thousands of years of evolution is an excellent base for a selection and breeding program. However, forest over-exploitation, establishment of other crops and urban development are hastening the elimination of Mexican race and other avocados, causing genetic erosion. We initiated this study of the avocado genetic resources with exploration and collection activities. We searched for outstanding types, taking into account vegetative growth, fruit quality, productivity and resistance to adverse conditions. We looked also for wild and semi-wild species related to the Persea genus. -

Coatepec Harinas Page 1 of 20
Estado de México - Coatepec Harinas Page 1 of 20 Enciclopedia de los Municipios de México ESTADO DE MÉXICO COATEPEC HARINAS Coatepec Harinas en línea NOMENCLATURA Denominación Coatepec Harinas Toponimia El nombre original es Coauhtepetl, que proviene del náhuatl, coauhtl, “culebra” “serpiente” y tepetl, “cerro”; que significa “cerro de las serpientes”. Probablemente en 1825, a raíz del auge harinero y la gran calidad de este producto, se le agregó el Harinas, para distinguirlo de otros pueblos con el mismo nombre. Glifo Es a partir de 1982, cuando el ayuntamiento en turno comienza a utilizar un escudo con las siguientes características: “Un cerro en el que sobresale medio cuerpo de serpiente, en su base dos semicírculos; el de arriba de color rojo y el de abajo amarillo, el cerro es de color verde, asentado sobre campo blanco, rodeado por cuatro magueyes en aparente perspectiva, al centro del campo blanco, tres tunas en floración, de color verde blanco y rojo, a los extremos de las figuras de un pan y otra irreconocible, en los extremos de http://www.e-local.gob.mx/work/templates/enciclo/mexico/mpios/15021a.htm 11/25/2005 Estado de México - Coatepec Harinas Page 2 of 20 todo este conjunto, cinco redondelas todo el conjunto está ribeteado por una franja verde azulosa de igual color los magueyes”. Significado El cerro es el lugar donde se asentaron los primeros pobladores, la serpiente se refiere a la existencia de una gran cantidad y variedad de estos ofidios crotálidos en donde, cuatro magueyes en referencia a los cuatro puntos cardinales, cinco redondelas o malacates en clara referencia a las cinco épocas transcurridas conforme a la leyenda Teotihuacana (Quinto Sol), y a la rueca en donde se hilaba la lana para la confección de los sarapes y gabanes que desde hace mucho son elaborados en Coatepec, el campo blanco, en referencia a la blancura de las nieves del Xinantécatl que dan vida a Coatepec al transformarse en agua y también en clara alusión a la blancura de la harina de gran calidad que se produjo en sus molinos; así como la figura de un pan.