DOCSLIB.ORG

From a Quantum-Electrodynamical Light–Matter Description to Novel Spectroscopies

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
From a Quantum-Electrodynamical Light–Matter Description to Novel Spectroscopies REVIEWS From a quantum-electrodynamical light–matter description to novel spectroscopies Michael Ruggenthaler1*, Nicolas Tancogne-Dejean1*, Johannes Flick1,3*, Heiko Appel1* and Angel Rubio1,2* Abstract | Insights from spectroscopic experiments led to the development of quantum mechanics as the common theoretical framework for describing the physical and chemical properties of atoms, molecules and materials. Later, a full quantum description of charged particles, electromagnetic radiation and special relativity was developed, leading to quantum electrodynamics (QED). This is, to our current understanding, the most complete theory describing photon–matter interactions in correlated many-body systems. In the low-energy regime, simplified models of QED have been developed to describe and analyse spectra over a wide spatiotemporal range as well as physical systems. In this Review, we highlight the interrelations and limitations of such theoretical models, thereby showing that they arise from low-energy simplifications of the full QED formalism, in which antiparticles and the internal structure of the nuclei are neglected. Taking molecular systems as an example, we discuss how the breakdown of some simplifications of low-energy QED challenges our conventional understanding of light–matter interactions. In addition to high-precision atomic measurements and simulations of particle physics problems in solid-state systems, new theoretical features that account for collective QED effects in complex interacting many-particle systems could become a material-based route to further advance our current understanding of light–matter interactions. Spectroscopy (from the Latin speciō ‘look at or view’ and now reaching sub-angstroms and atto seconds. The dif- 1Max Planck Institute for the Greek skopéō ‘to see’) investigates the various properties ferent static and time-resolved spectro scopic techniques Structure and Dynamics of of physical systems over different space, time and energy encompass optical (vibrational, rotational and electronic), Matter and Center for Free- scales by looking at their response to different pertur- magnetic, magnetic-resonance (nuclear and electron Electron Laser Science, bations. The different particles (electrons, protons and spin-resonance), energy-loss, mechanical (atomic force), Hamburg, Germany. 2Center for Computational neutrons) taking part in a physico-chemical process, transport (electronic, spin or heat), and imaging (diffrac- Quantum Physics (CCQ), electro magnetic and thermal radiations or mechanical tion, scanning-tunnelling microscopy and holography) The Flatiron Institute, New deformations can be investigated and simultaneously spectroscopies. Therefore, it is no longer possible to refer York, NY, USA. used as perturbations. In atomic, molecular and solid- to ‘spectroscopy’ without specifying the technique or the 3 Present address: John state physics, spectroscopic methods are specifically spatial and temporal regime. A. Paulson School of Engineering and Applied used to probe and control various aspects of coupled Diverse spectroscopic techniques are applied in differ- 11 Sciences, Harvard University, photon–matter systems, such as the quantum nature of ent fields — from atomic and molecular physics to solid- Cambridge, MA, USA. light1, matter–matter interactions2, electronic3 and nuclear state physics12 and biochemistry13 — and the analysis *e-mail: michael. degrees of freedom4 and collective effects in molecular and and interpretation of the complex experimental data in [email protected]; solid-state systems5. The study of these photon–matter each of these fields are routinely performed by means nicolas.tancogne-dejean@ interactions has informed us, for example, on unknown of purpose-built theoretical tools. These theoretical mpsd.mpg.de; 6,7 [email protected]; states of matter , novel equilibrium and non-equilibrium tools often treat electromagnetic radiation and matter at 8 [email protected]; (driven) topological phases and light-induced super- different levels of approximation, thereby limiting their use [email protected] conductivity9. Over the years, the development and pro- to only particular cases. Usually, photons are considered doi:10.1038/s41570-018-0118 gress of specific experimental spectroscopic techniques only as an external perturbation (often treated classically) Published online 7 Mar 2018 have resulted in remarkable spatial and time resolutions3,10, that probes matter (treated quantum mechanically), NATURE REVIEWS | CHEMISTRY VOLUME 2 | ARTICLE NUMBER 0118 | 1 ©2018 Mac millan Publishers Li mited, part of Spri nger Nature. All ri ghts reserved. REVIEWS whereas the self-consistent back-reaction of matter on equation with the Maxwell equations. The spectrum is photons is neglected. Standard theoretical modelling interpreted as transitions between atomic states, each one can thus be insufficient when the degrees of freedom of interacting or dressed with the classical Maxwell field. photons and matter become equally important. Strong The use of the dressed-electron picture has been known light–matter interaction, as in the case of polariton conden- for a long time, and the coupled Schrödinger–Maxwell sates14, provides a direct example. However, the interaction or Dirac–Maxwell equations form the basic framework between photons and matter, beyond the semi-classical to describe molecular and solid-state spectros copies. description, is also expected to play a role under other However, it is also clear that these equations are simplifi- conditions and could lead, for instance, to the emergence cations of an even more complete theory, which explicitly of collective responses in ensembles of molecules. takes into account the electromagnetic degrees of freedom In this Review, we take a step back from the ever- on a quantized level. Indeed, many experimental results increasing specialization of each of the current theoretical exist that require the simultaneous consideration of the approaches and scrutinize them as different low-energy quantum nature of electrons and the electro magnetic approximations of the general framework of quantum degrees of freedom (see FIG. 1 for a schematic of the evo- electrodynamics (QED). In particular, we focus on lution of our understanding of combined light–matter non-relativistic QED, which is applicable within the typical systems). These include the modification of atomic energy and timescales of molecular and solid-state energy levels in high-Q cavities23, the emergence of quasi- spectros copies (from a few millielectronvolts to a few particles24 such as polaritons, and spectroscopies that thousand electronvolts and from attoseconds to milli- make use of the quantum nature of light22. Traditionally, seconds). A great amount of theoretical and experimental many of these electromagnetic effects (for example, the techniques have been developed to study photon–matter Lamb shift or the finite lifetime of an excited molecular interactions in these energetic and temporal regimes, and state) have been investigated in atomic and small molec- it is beyond the scope of this Review to describe them all or ular systems23,25,26. Although usually small for isolated to provide a comprehensive list of examples; however, we atoms, these electromagnetic effects have an important refer to the relevant literature where possible. We consider role in molecular systems and even more in solid-state mainly optical and electronic spectroscopies, focusing on systems, leading, for example, to the following: the electron–photon phenomena in molecular and solid- screening, polarization and retardation effects observed state systems; we do not explicitly examine direct proton– in light–matter energy transfer induced by attosecond photon interactions but instead describe the nuclei laser pulses27; the emergence of quasi-particles that do (consisting of protons and neutrons) as effective particles. not have a classical counterpart, such as polaritons or Similar considerations can be extended straightforwardly axions28,29; and the formation of novel states of matter, to this additional case. We highlight the limitations of the such as hybrid photon–matter states30,31, exciton–polariton theoretical tools used to describe photon–matter inter- condensates14,32 or light-induced topological states8. Well- actions but also identify new phenomena and hidden known electromagnetic effects in quantum chemistry aspects of these interactions that can be revealed with and solid-state physics33 are long-range intermolecular the development of new tailored spectroscopic tools. interactions and Casimir–Polder forces34,35, Förster reso- 36,37 Polariton When matter and photons are strongly correlated, novel nance energy transfer or the hydrodynamical regime A polariton is a bosonic effects appear, such as changes in the chemical proper- of quantum light38. However, most common theoretical quasi-particle formed by an ties of molecules in optical cavities and the emergence of approaches do not treat these effects self-consistently, excitation, such as an exciton polaritonic chemistry15,16,17,18, strong photon coupling in light- meaning that they do not consider the back-reaction of or plasmon coupled (‘dressed’) 19 with photons. harvesting complexes or attraction between photons matter on the electromagnetic field and vice versa. due to quantum matter20. Such effects have the potential QED provides a general framework to treat electro- Polaritonic chemistry to directly challenge
Load more

Recommended publications
  • Quantum Optics: an Introduction
    The Himalayan Physics, Vol.1, No.1, May 2010 Quantum Optics: An Introduction Min Raj Lamsal Prithwi Narayan Campus, Pokhara Email: [email protected] Optics is the physics, which deals with the study of in electrodynamics gave beautiful and satisfactory nature of light, its propagation in different media description of the electromagnetic phenomena. At (including vacuum) & its interaction with different the same time, the kinetic theory of gases provided materials. Quantum is a packet of energy absorbed or a microscopic basis for the thermo dynamical emitted in the form of tiny packets called quanta. It properties of matter. Up to the end of the nineteenth means the amount of energy released or absorbed in century, the classical physics was so successful a physical process is always an integral multiple of and impressive in explaining physical phenomena a discrete unit of energy known as quantum which is that the scientists of that time absolutely believed also known as photon. Quantum Optics is a fi eld of that they were potentially capable of explaining all research in physics, dealing with the application of physical phenomena. quantum mechanics to phenomena involving light and its interactions with matter. However, the fi rst indication of inadequacy of the Physics in which majority of physical phenomena classical physics was seen in the beginning of the can be successfully described by using Newton’s twentieth century where it could not explain the laws of motion is called classical physics. In fact, the experimentally observed spectra of a blackbody classical physics includes the classical mechanics and radiation. In addition, the laws in classical physics the electromagnetic theory.
    [Show full text]
  • Quantum Field Theory*
    Quantum Field Theory y Frank Wilczek Institute for Advanced Study, School of Natural Science, Olden Lane, Princeton, NJ 08540 I discuss the general principles underlying quantum eld theory, and attempt to identify its most profound consequences. The deep est of these consequences result from the in nite number of degrees of freedom invoked to implement lo cality.Imention a few of its most striking successes, b oth achieved and prosp ective. Possible limitation s of quantum eld theory are viewed in the light of its history. I. SURVEY Quantum eld theory is the framework in which the regnant theories of the electroweak and strong interactions, which together form the Standard Mo del, are formulated. Quantum electro dynamics (QED), b esides providing a com- plete foundation for atomic physics and chemistry, has supp orted calculations of physical quantities with unparalleled precision. The exp erimentally measured value of the magnetic dip ole moment of the muon, 11 (g 2) = 233 184 600 (1680) 10 ; (1) exp: for example, should b e compared with the theoretical prediction 11 (g 2) = 233 183 478 (308) 10 : (2) theor: In quantum chromo dynamics (QCD) we cannot, for the forseeable future, aspire to to comparable accuracy.Yet QCD provides di erent, and at least equally impressive, evidence for the validity of the basic principles of quantum eld theory. Indeed, b ecause in QCD the interactions are stronger, QCD manifests a wider variety of phenomena characteristic of quantum eld theory. These include esp ecially running of the e ective coupling with distance or energy scale and the phenomenon of con nement.
    [Show full text]
  • The Concept of Quantum State : New Views on Old Phenomena Michel Paty
    The concept of quantum state : new views on old phenomena Michel Paty To cite this version: Michel Paty. The concept of quantum state : new views on old phenomena. Ashtekar, Abhay, Cohen, Robert S., Howard, Don, Renn, Jürgen, Sarkar, Sahotra & Shimony, Abner. Revisiting the Founda- tions of Relativistic Physics : Festschrift in Honor of John Stachel, Boston Studies in the Philosophy and History of Science, Dordrecht: Kluwer Academic Publishers, p. 451-478, 2003. halshs-00189410 HAL Id: halshs-00189410 https://halshs.archives-ouvertes.fr/halshs-00189410 Submitted on 20 Nov 2007 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. « The concept of quantum state: new views on old phenomena », in Ashtekar, Abhay, Cohen, Robert S., Howard, Don, Renn, Jürgen, Sarkar, Sahotra & Shimony, Abner (eds.), Revisiting the Foundations of Relativistic Physics : Festschrift in Honor of John Stachel, Boston Studies in the Philosophy and History of Science, Dordrecht: Kluwer Academic Publishers, 451-478. , 2003 The concept of quantum state : new views on old phenomena par Michel PATY* ABSTRACT. Recent developments in the area of the knowledge of quantum systems have led to consider as physical facts statements that appeared formerly to be more related to interpretation, with free options.
    [Show full text]
  • On the Definition of the Renormalization Constants in Quantum Electrodynamics
    On the Definition of the Renormalization Constants in Quantum Electrodynamics Autor(en): Källén, Gunnar Objekttyp: Article Zeitschrift: Helvetica Physica Acta Band(Jahr): 25(1952) Heft IV Erstellt am: Mar 18, 2014 Persistenter Link: http://dx.doi.org/10.5169/seals-112316 Nutzungsbedingungen Mit dem Zugriff auf den vorliegenden Inhalt gelten die Nutzungsbedingungen als akzeptiert. Die angebotenen Dokumente stehen für nicht-kommerzielle Zwecke in Lehre, Forschung und für die private Nutzung frei zur Verfügung. Einzelne Dateien oder Ausdrucke aus diesem Angebot können zusammen mit diesen Nutzungsbedingungen und unter deren Einhaltung weitergegeben werden. Die Speicherung von Teilen des elektronischen Angebots auf anderen Servern ist nur mit vorheriger schriftlicher Genehmigung möglich. Die Rechte für diese und andere Nutzungsarten der Inhalte liegen beim Herausgeber bzw. beim Verlag. Ein Dienst der ETH-Bibliothek Rämistrasse 101, 8092 Zürich, Schweiz [email protected] http://retro.seals.ch On the Definition of the Renormalization Constants in Quantum Electrodynamics by Gunnar Källen.*) Swiss Federal Institute of Technology, Zürich. (14.11.1952.) Summary. A formulation of quantum electrodynamics in terms of the renor- malized Heisenberg operators and the experimental mass and charge of the electron is given. The renormalization constants are implicitly defined and ex¬ pressed as integrals over finite functions in momentum space. No discussion of the convergence of these integrals or of the existence of rigorous solutions is given. Introduction. The renormalization method in quantum electrodynamics has been investigated by many authors, and it has been proved by Dyson1) that every term in a formal expansion in powers of the coupling constant of various expressions is a finite quantity.
    [Show full text]
  • THE DEVELOPMENT of the SPACE-TIME VIEW of QUANTUM ELECTRODYNAMICS∗ by Richard P
    THE DEVELOPMENT OF THE SPACE-TIME VIEW OF QUANTUM ELECTRODYNAMICS∗ by Richard P. Feynman California Institute of Technology, Pasadena, California Nobel Lecture, December 11, 1965. We have a habit in writing articles published in scientific journals to make the work as finished as possible, to cover all the tracks, to not worry about the blind alleys or to describe how you had the wrong idea first, and so on. So there isn’t any place to publish, in a dignified manner, what you actually did in order to get to do the work, although, there has been in these days, some interest in this kind of thing. Since winning the prize is a personal thing, I thought I could be excused in this particular situation, if I were to talk personally about my relationship to quantum electrodynamics, rather than to discuss the subject itself in a refined and finished fashion. Furthermore, since there are three people who have won the prize in physics, if they are all going to be talking about quantum electrodynamics itself, one might become bored with the subject. So, what I would like to tell you about today are the sequence of events, really the sequence of ideas, which occurred, and by which I finally came out the other end with an unsolved problem for which I ultimately received a prize. I realize that a truly scientific paper would be of greater value, but such a paper I could publish in regular journals. So, I shall use this Nobel Lecture as an opportunity to do something of less value, but which I cannot do elsewhere.
    [Show full text]
  • The Massless Two-Loop Two-Point Function and Zeta Functions in Counterterms of Feynman Diagrams
    The Massless Two-loop Two-point Function and Zeta Functions in Counterterms of Feynman Diagrams Dissertation zur Erlangung des Grades \Doktor der Naturwissenschaften" am Fachbereich Physik der Johannes-Gutenberg-Universit¨at in Mainz Isabella Bierenbaum geboren in Landau/Pfalz Mainz, Februar 2005 Datum der mundlic¨ hen Prufung:¨ 6. Juni 2005 D77 (Diss. Universit¨at Mainz) Contents 1 Introduction 1 2 Renormalization 3 2.1 General introduction . 3 2.2 Feynman diagrams and power counting . 5 2.3 Dimensional regularization . 9 2.4 Counterterms . 10 2.4.1 One-loop diagrams . 10 2.4.2 Multi-loop diagrams . 11 3 Hopf and Lie algebra 15 3.1 The Hopf algebras HR and HF G . 15 3.1.1 The Hopf algebra of rooted trees HR . 16 3.1.2 The Hopf algebra of Feynman graphs HF G . 20 3.1.3 Correspondence between HR, HF G, and ZFF . 20 3.2 Lie algebras . 24 4 The massless two-loop two-point function | an overview 27 4.1 General remarks . 27 4.2 Integer exponents νi | the triangle relation . 29 4.3 Non-integer exponents νi . 32 5 Nested sums 37 5.1 Nested sums . 38 5.1.1 From polylogarithms to multiple polylogarithms . 38 5.1.2 Algebraic relations: shuffle and quasi-shuffle . 41 5.2 nestedsums | the theory and some of its functions . 45 5.2.1 nestedsums | the general idea . 46 5.2.2 nestedsums | the four classes of functions . 48 6 The massless two-loop two-point function 53 6.1 The expansion of I^(2;5) . 53 6.1.1 Decomposition of I^(2;5) .
    [Show full text]
  • Arxiv:1202.1557V1
    The Heisenberg-Euler Effective Action: 75 years on ∗ Gerald V. Dunne Physics Department, University of Connecticut, Storrs, CT 06269-3046, USA On this 75th anniversary of the publication of the Heisenberg-Euler paper on the full non- perturbative one-loop effective action for quantum electrodynamics I review their paper and discuss some of the impact it has had on quantum field theory. I. HISTORICAL CONTEXT After the 1928 publication of Dirac’s work on his relativistic theory of the electron [1], Heisenberg immediately appreciated the significance of the new ”hole theory” picture of the quantum vacuum of quantum electrodynamics (QED). Following some confusion, in 1931 Dirac associated the holes with positively charged electrons [2]: A hole, if there were one, would be a new kind of particle, unknown to experimental physics, having the same mass and opposite charge to an electron. With the discovery of the positron in 1932, soon thereafter [but, interestingly, not immediately [3]], Dirac proposed at the 1933 Solvay Conference that the negative energy solutions [holes] should be identified with the positron [4]: Any state of negative energy which is not occupied represents a lack of uniformity and this must be shown by observation as a kind of hole. It is possible to assume that the positrons are these holes. Positron theory and QED was born, and Heisenberg began investigating positron theory in earnest, publishing two fundamental papers in 1934, formalizing the treatment of the quantum fluctuations inherent in this Dirac sea picture of the QED vacuum [5, 6]. It was soon realized that these quantum fluctuations would lead to quantum nonlinearities [6]: Halpern and Debye have already independently drawn attention to the fact that the Dirac theory of the positron leads to the scattering of light by light, even when the energy of the photons is not sufficient to create pairs.
    [Show full text]
  • Vacuum Energy
    Vacuum Energy Mark D. Roberts, 117 Queen’s Road, Wimbledon, London SW19 8NS, Email:[email protected] http://cosmology.mth.uct.ac.za/ roberts ∼ February 1, 2008 Eprint: hep-th/0012062 Comments: A comprehensive review of Vacuum Energy, which is an extended version of a poster presented at L¨uderitz (2000). This is not a review of the cosmolog- ical constant per se, but rather vacuum energy in general, my approach to the cosmological constant is not standard. Lots of very small changes and several additions for the second and third versions: constructive feedback still welcome, but the next version will be sometime in coming due to my sporadiac internet access. First Version 153 pages, 368 references. Second Version 161 pages, 399 references. arXiv:hep-th/0012062v3 22 Jul 2001 Third Version 167 pages, 412 references. The 1999 PACS Physics and Astronomy Classification Scheme: http://publish.aps.org/eprint/gateway/pacslist 11.10.+x, 04.62.+v, 98.80.-k, 03.70.+k; The 2000 Mathematical Classification Scheme: http://www.ams.org/msc 81T20, 83E99, 81Q99, 83F05. 3 KEYPHRASES: Vacuum Energy, Inertial Mass, Principle of Equivalence. 1 Abstract There appears to be three, perhaps related, ways of approaching the nature of vacuum energy. The first is to say that it is just the lowest energy state of a given, usually quantum, system. The second is to equate vacuum energy with the Casimir energy. The third is to note that an energy difference from a complete vacuum might have some long range effect, typically this energy difference is interpreted as the cosmological constant.
    [Show full text]
  • Feynman Quantization
    3 FEYNMAN QUANTIZATION An introduction to path-integral techniques Introduction. By Richard Feynman (–), who—after a distinguished undergraduate career at MIT—had come in as a graduate student to Princeton, was deeply involved in a collaborative effort with John Wheeler (his thesis advisor) to shake the foundations of field theory. Though motivated by problems fundamental to quantum field theory, as it was then conceived, their work was entirely classical,1 and it advanced ideas so radicalas to resist all then-existing quantization techniques:2 new insight into the quantization process itself appeared to be called for. So it was that (at a beer party) Feynman asked Herbert Jehle (formerly a student of Schr¨odinger in Berlin, now a visitor at Princeton) whether he had ever encountered a quantum mechanical application of the “Principle of Least Action.” Jehle directed Feynman’s attention to an obscure paper by P. A. M. Dirac3 and to a brief passage in §32 of Dirac’s Principles of Quantum Mechanics 1 John Archibald Wheeler & Richard Phillips Feynman, “Interaction with the absorber as the mechanism of radiation,” Reviews of Modern Physics 17, 157 (1945); “Classical electrodynamics in terms of direct interparticle action,” Reviews of Modern Physics 21, 425 (1949). Those were (respectively) Part III and Part II of a projected series of papers, the other parts of which were never published. 2 See page 128 in J. Gleick, Genius: The Life & Science of Richard Feynman () for a popular account of the historical circumstances. 3 “The Lagrangian in quantum mechanics,” Physicalische Zeitschrift der Sowjetunion 3, 64 (1933). The paper is reprinted in J.
    [Show full text]
  • The QED Coupling Constant for an Electron to Emit Or Absorb a Photon Is Shown to Be the Square Root of the Fine Structure Constant Α Shlomo Barak
    The QED Coupling Constant for an Electron to Emit or Absorb a Photon is Shown to be the Square Root of the Fine Structure Constant α Shlomo Barak To cite this version: Shlomo Barak. The QED Coupling Constant for an Electron to Emit or Absorb a Photon is Shown to be the Square Root of the Fine Structure Constant α. 2020. hal-02626064 HAL Id: hal-02626064 https://hal.archives-ouvertes.fr/hal-02626064 Preprint submitted on 26 May 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. V4 15/04/2020 The QED Coupling Constant for an Electron to Emit or Absorb a Photon is Shown to be the Square Root of the Fine Structure Constant α Shlomo Barak Taga Innovations 16 Beit Hillel St. Tel Aviv 67017 Israel Corresponding author: [email protected] Abstract The QED probability amplitude (coupling constant) for an electron to interact with its own field or to emit or absorb a photon has been experimentally determined to be -0.08542455. This result is very close to the square root of the Fine Structure Constant α. By showing theoretically that the coupling constant is indeed the square root of α we resolve what is, according to Feynman, one of the greatest damn mysteries of physics.
    [Show full text]
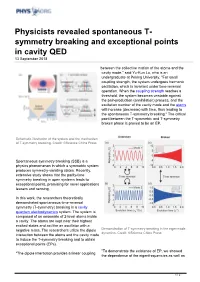
  • Symmetry Breaking and Exceptional Points in Cavity QED 13 September 2018
    Physicists revealed spontaneous T- symmetry breaking and exceptional points in cavity QED 13 September 2018 between the collective motion of the atoms and the cavity mode," said Yu-Kun Lu, who is an undergraduate at Peking University. "For small coupling strength, the system undergoes harmonic oscillation, which is invariant under time-reversal operation. When the coupling strength reaches a threshold, the system becomes unstable against the pair-production (annihilation) process, and the excitation number of the cavity mode and the atoms will increase (decrease) with time, thus leading to the spontaneous T-symmetry breaking." The critical point between the T-symmetric and T-symmetry broken phase is proved to be an EP. Schematic illustration of the system and the mechanism of T-symmetry breaking. Credit: ©Science China Press Spontaneous symmetry breaking (SSB) is a physics phenomenon in which a symmetric system produces symmetry-violating states. Recently, extensive study shows that the parity-time symmetry breaking in open systems leads to exceptional points, promising for novel applications leasers and sensing. In this work, the researchers theoretically demonstrated spontaneous time-reversal symmetry (T-symmetry) breaking in a cavity quantum electrodynamics system. The system is composed of an ensemble of 2-level atoms inside a cavity. The atoms are kept near their highest excited states and act like an oscillator with a negative mass. The researchers utilize the dipole Demonstration of T-symmetry breaking in the eigenmode dynamics. Credit: ©Science China Press interaction between the atoms and the cavity mode to induce the T-symmetry breaking and to obtain exceptional points (EPs). "To demonstrate the existence of EP, we showed "The dipole interaction provides a linear coupling the dependence of the eigenfrequencies as well as 1 / 2 the eigenmode on the cavity-atom detuning, and we found they coalesce at the critical point, and thus proved it to be an EP," said Pai Peng, a former undergraduate in Prof.
    [Show full text]
  • Structure of Vacuum in Chiral Supersymmetric Quantum Electrodynamics A
    Structure of vacuum in chiral supersymmetric quantum electrodynamics A. V. Smilga Institute of Theoretical and Experimental Physics, Academy of Sciences of the USSR, Moscow (Submitted 21 January 1986) Zh. Eksp. Teor. Fiz. 91, 14-24 (July 1986) An effective Hamiltonian is found for supersymmetric quantum electrodynamics defined in a finite volume. When the right and left fields appear in the theory nonsymmetrically (but so that anomalies cancel out), this Hamiltonian turns out to be nontrivial and describes the motion of a particle in the "ionic crystal" consisting of magnetic charges of different sign with an additional scalar potential of the form U = K '/2, where aiK = z..Despite the nontrivial form of the effective Hamiltonian, supersymmetry remains unbroken. 1. INTRODUCTION analysis of nonchiral theories. We shall investigate the sim- One of the most acute problems in theoretical elemen- plest example of chiral supersymmetric QCD. Unfortunate- tary-particle physics is the question of supersymmetry ly, our original hopes have not been justified, and supersym- breaking, which is generally believed to occur in nature in metry remains unbroken in this theory. The effective one form or another at high enough energies. The most at- Hamiltonian has, however, turned out to be highly nontri- tractive mechanism of supersymmetry breaking is spontane- vial and does not reduce to free motion, as was the case for ous breaking by dynamic effects, not manifest at the "tree" nonchiral theories. The methods developed below can be level. A well-known example of this type of breaking occurs used in the analysis of more complicated chiral theories, in- in the Witten quantum mechanics with superpotential of the cluding those in which supersymmetry is definitely broken.
    [Show full text]