DOCSLIB.ORG

Unit 4: Surface Area and Volume of Solids Lesson 4.1 Explore Solids Lesson 12.1 from Textbook

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unit 4: Surface Area and Volume of Solids Lesson 4.1 Explore Solids Lesson 12.1 from Textbook Unit 4: Surface Area and Volume of Solids Lesson 4.1 Explore Solids Lesson 12.1 from textbook Objectives: • Determine which of the different three-dimensional figures or solids are polyhedra • Identify parts of the polyhedron such as faces, vertices, and edges. • Identify the solids formed by taking cross sections of a polyhedron. face Face __________________________________________ edge Edge __________________________________________ Vertex _________________________________________ vertex Regular, Convex Polyhedron Nonregular, Concave Polyhedron TYPES OF SOLIDS Polyhedra Not Polyhedra Prism Pyramid Cone Cylinder CLASSIFYING SOLIDS To classify a polyhedron, ______________________________________________________. Polyhedron Type of Polyhedron Shape of Base Name of Polyhedron Example 1 Tell whether the solid is a polyhedron. If it is, name the polyhedron and find its number of faces, vertices, and edges. ______________________________________________________ Euler’s Theorem The number of faces, vertices, and edges of a polyhedron are related by the formula ______________________. CROSS SECTIONS Cross Section ________________________________ Example 2 Describe the shape formed by the intersection of the plane and the cube. ___________________ ____________________ Unit 4.2: Surface Area and Volume of Solids Lesson 4.2 Surface Area of Prisms and Cylinders Lesson 12.2 from textbook Objectives: • Derive the formula for surface area of a prism and a cylinder using the area formulas for parallelograms and circles. • Use the formulas to calculate the surface area of a prism and a cylinder. • Use the surface area of a prism or cylinder to find the unknown dimensions. PRISMS Name of Prism ______________________________________ Number of Bases ____________________________________ Number of Lateral Faces ______________________________ NET OF A RECTANGULAR PRISM Lateral Area = _____________ Base Area = _______________ Surface Area = _________________ OBLIQUE AND RIGHT PRISMS Surface Area of a Right Prism Theorem Example 1 P = perimeter of base, B = base Area, h = height of prism Find the surface area of the right prism. S = __________________________ S = ___________________________ CYLINDERS NET OF A CYLINDER Shape of Base _______________ Base Area = _______________ Lateral Area = _______________ Surface Area = ______________________ Surface Area of a Cylinder Theorem Example 2 r = radius of base, h = height of the cylinder Find the surface area of the cylinder. S = ____________________________ S = ____________________________ Example 3 Find the height of the right cylinder which has a surface area of 157.08 square meters. h = ___________________________ Unit 4: Surface Area and Volume of Solids Lesson 4.3 Surface Area of Pyramids and Cones Lesson 12.3 from textbook Objectives: • Derive the formula for surface area of a pyramid and a cone using the area formulas for parallelograms, triangles and circles. • Use the formulas to calculate the surface area of a pyramid and a cone. • Use the surface area of a pyramid or cone to find the unknown dimensions. PYRAMIDS NET OF A PYRAMID l = _____________________ b = ____________________ Lateral Area _____________________________ Surface Area = ___________________________ Surface Area of a Pyramid Theorem Example 1 B = base area, P = perimeter of the base, l = slant height Find the lateral area of the pyramid. S = _________________________ L = ____________________________ Example 2 Find the surface area of the pyramid. S = ____________________________ CONES NET OF A RIGHT CONE Base Area ______________________ Lateral Area ____________________ Surface Area ____________________ Surface Area for Cones Theorem r = radius of the base, l = slant height of cone S = _________________ Example 3 Find the surface area of the cone. S = ___________________________ S = ___________________________ Unit 4: Surface Area and Volume of Solids Lesson 4.4: Volume of Prisms and Cylinders Lesson 12.4 from textbook Objectives: • Use the formulas to calculate the volume of a prism and a cylinder. • Use the volume of a prism or cylinder to find the unknown dimensions. • Solve problems involving unit conversion for situations involving volumes within the same measurement system. Volume of a Cube Postulate Volume Congruence Postulate The volume of a cube is the cube of If two polyhedra are congruent, then the length of its side. their volumes _____________________________. Volume Addition Postulate. V = _______________________ The volume of a solid is the sum of the volume of its non-overlapping parts. Volume of a Prism Volume of a Cylinder B = Base area, h = height of prism B = Base area, h = height of prism V = _______________________ V = Bh = _________________________ *The shape of the base could be a square, rectangle, trapezoid, triangle, or any polygon. Example 1 Find the volume of the solid. V = ______________________ V = _____________________ Example 2 If the volume of the cube is 90 in 3, find the length of each side x. x = ________________ x x x Cavalieri’s Principle Example 3 Find the volume of the solid. All three solids have equal heights and cross-sectional areas B. Bonaventura Cavalieri stated that: ____________________________________ ________________________ Example 4 Example 5 Find the volume of the solid. The sculpture is made of 13 beams. The dimensions of each beam are 30 by 30 by 90. Find its volume. V = ____________________ V = ____________________ Unit 4: Surface Area and Volume of Solids Lesson 4.5 Volume of Pyramids and Cones Lesson 4.5 from textbook Objectives: • Use the formulas to calculate the volume of a pyramid and cone. • Use the volume of a pyramid and cone to find the unknown dimensions. • Solve problems involving unit conversion for situations involving volumes within the same measurement system. Volume of a Pyramid Theorem Volume of a Cone Theorem V = _____________________________ V = _____________________________ Example 1 Find the volume of the solid. V = _________________ V ≈ __________________ Example 2 If a square base pyramid has a height of 144 meters and a volume of 2,226,450 m 3, what are the dimensions of the base? x = ____________________ Example 3 Find the volume of the right cone. V ≈ _________________________ Example 4 Find the volume of the solid shown. V = _____________________ Example 5 Unit 4: Surface Area and Volume of Solids Lesson 4.6 Surface Area and Volume of Spheres Lesson 12.6 from textbook Objectives: • Identify the different parts of the sphere: center, radius, diameter, and great circle. • Use the given formulas to find the surface area and volume of a sphere. • Use the given volume and surface area to find the unknown measures of the sphere. • Solve problems involving unit conversion for situations involving volumes within the same measurement system. SPHERE GREAT CIRCLES and HEMISPHERES Surface Area of a Sphere Theorem S = __________________________ Example 1 Example 2 Find the surface area of the sphere. Find the radius of the sphere if the surface area is 228 cm 2. r = ___________________ S = _________________________ Example 3 Find the surface area of the composite solid. S = ____________________ Volume of a Sphere Theorem Example 4 Find the volume of the sphere. V = _____________________ V = ______________________________ Example 5 Find the volume of the composite solid. V = ______________________________ Example 6 .
Load more

Recommended publications
  • Arc Length. Surface Area
    Calculus 2 Lia Vas Arc Length. Surface Area. Arc Length. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: The arc length L of f(x) for a ≤ x ≤ b can be obtained by integrating the length element ds from a to b: The length element ds on a sufficiently small interval can be approximated by the hypotenuse of a triangle with sides dx and dy: p Thus ds2 = dx2 + dy2 ) ds = dx2 + dy2 and so s s Z b Z b q Z b dy2 Z b dy2 L = ds = dx2 + dy2 = (1 + )dx2 = (1 + )dx: a a a dx2 a dx2 2 dy2 dy 0 2 Note that dx2 = dx = (y ) : So the formula for the arc length becomes Z b q L = 1 + (y0)2 dx: a Area of a surface of revolution. Suppose that y = f(x) is a continuous function with a continuous derivative on [a; b]: To compute the surface area Sx of the surface obtained by rotating f(x) about x-axis on [a; b]; we can integrate the surface area element dS which can be approximated as the product of the circumference 2πy of the circle with radius y and the height that is given by q the arc length element ds: Since ds is 1 + (y0)2dx; the formula that computes the surface area is Z b q 0 2 Sx = 2πy 1 + (y ) dx: a If y = f(x) is rotated about y-axis on [a; b]; then dS is the product of the circumference 2πx of the circle with radius x and the height that is given by the arc length element ds: Thus, the formula that computes the surface area is Z b q 0 2 Sy = 2πx 1 + (y ) dx: a Practice Problems.
    [Show full text]
  • Cones, Pyramids and Spheres
    The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 YEARS 910 Cones, Pyramids and Spheres (Measurement and Geometry : Module 12) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 12 CONES, PYRAMIDS AND SPHERES A guide for teachers - Years 9–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 910 {4} A guide for teachers CONES, PYRAMIDS AND SPHERES ASSUMED KNOWLEDGE • Familiarity with calculating the areas of the standard plane figures including circles. • Familiarity with calculating the volume of a prism and a cylinder. • Familiarity with calculating the surface area of a prism. • Facility with visualizing and sketching simple three‑dimensional shapes. • Facility with using Pythagoras’ theorem. • Facility with rounding numbers to a given number of decimal places or significant figures.
    [Show full text]
  • Lateral and Surface Area of Right Prisms 1 Jorge Is Trying to Wrap a Present That Is in a Box Shaped As a Right Prism
    CHAPTER 11 You will need Lateral and Surface • a ruler A • a calculator Area of Right Prisms c GOAL Calculate lateral area and surface area of right prisms. Learn about the Math A prism is a polyhedron (solid whose faces are polygons) whose bases are congruent and parallel. When trying to identify a right prism, ask yourself if this solid could have right prism been created by placing many congruent sheets of paper on prism that has bases aligned one above the top of each other. If so, this is a right prism. Some examples other and has lateral of right prisms are shown below. faces that are rectangles Triangular prism Rectangular prism The surface area of a right prism can be calculated using the following formula: SA 5 2B 1 hP, where B is the area of the base, h is the height of the prism, and P is the perimeter of the base. The lateral area of a figure is the area of the non-base faces lateral area only. When a prism has its bases facing up and down, the area of the non-base faces of a figure lateral area is the area of the vertical faces. (For a rectangular prism, any pair of opposite faces can be bases.) The lateral area of a right prism can be calculated by multiplying the perimeter of the base by the height of the prism. This is summarized by the formula: LA 5 hP. Copyright © 2009 by Nelson Education Ltd. Reproduction permitted for classrooms 11A Lateral and Surface Area of Right Prisms 1 Jorge is trying to wrap a present that is in a box shaped as a right prism.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Comparing Surface Area & Volume
    Name ___________________________________________________________________ Period ______ Comparing Surface Area & Volume Use surface area and volume calculations to solve the following situations. 1. Find the surface area and volume of each prism. Which two have the same surface area? Which two have the same volume? 4 in. 22 in. 10 in. C A 11 in. B 18 in. 10 in. 6 in. 10 in. 6 in. 2. Sketch and label two different rectangular prisms that have the same volume. Find the surface area of each. 3. Do the following cylinders have the same surface area, the same volume, or the same surface area and volume? r = 4 cm r = 2 cm h = 9 cm h = 24 cm 4. A cylinder has a surface area of 125.6 mm2 and a volume of 100.48 mm3. If another cylinder has a radius of 5 mm and the same volume, what would be the height? 5. A cylinder has a radius of 9 yd and a height of 3 yd. A second cylinder has a radius of 6 yd and a height of 12 yd. Which statement is true? a. The cylinders have the same surface area and the same volume. b. The cylinders have the same surface area and different volumes. c. The cylinders have different surface areas and the same volume. d. The cylinders have different surface areas and different volumes. 6. The surface area of a rectangular prism is 2,116 mm2. If you double the length, width, and height of the prism, what will be the surface area of the new prism? How much larger is this amount? 7.
    [Show full text]
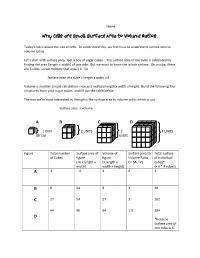
  • Why Cells Are Small: Surface Area to Volume Ratios
    Name__________________________________ Why Cells are Small: Surface Area to Volume Ratios Today’s lab is about the size of cells. To understand this, we first have to understand surface area to volume ratios. Let’s start with surface area. Get a box of sugar cubes. The surface area of the cube is calculated by finding the area (length x width) of one side. But we want to know the whole surface. On a cube, there are 6 sides, so we multiply that area x 6. So Surface area of a cube = length x width x 6 Volume is another simple calculation – we just multiply length x width x height. Build the following four structures from your sugar cubes, and fill out the table below. The one we’re most interested in, though is the surface area to volume ratio, which is just Surface area ÷ volume A B C D 1 UNIT 2 UNITS 3 4 UNITS OR CM UNITS Figure Total number Surface area of Volume of Surface area to Total surface of Cubes figure figure Volume Ratio of individual (=6 x length x (= length x ( = SA / V) cubes* width) width x height) (= 6 * # cubes) A 1 6 1 6 1 B 8 24 8 3 48 C 27 54 27 2 162 64 96 64 1.5 384 D *because surface area of one cube is 6 Surface Area to Volume Lab Questions 1. What happened to the surface area as the size increased? It increased. 2. What happened to the volume as the size increased? It also increased, but not as quickly.
    [Show full text]
  • Surface Area of 3-D Objects: Prisms: a Prism Is a Polyhedron with Two Opposite Faces That Are Identical Polygonal Regions Called the Bases
    Surface Area of 3-d Objects: Prisms: A prism is a polyhedron with two opposite faces that are identical polygonal regions called the bases. The vertices of the bases are joined with segments to form the lateral faces which are parallelograms. If the lateral faces are rectangles, the prism is called a right prism, otherwise, it’s called an oblique prism. oblique right The surface area is the sum of the areas of the two bases and the areas of the lateral faces. Right rectangular prism: Right triangular prism: 5 ft 7” 4 ft 5 ft 3 ft 3” 4” 1 2 SA..243 =( )( ) + 247( )( ) + 237( )( ) SA. .=( 3)( 5) + 2 ( 3)( 4) +( 4)( 5) + ( 5) 2 bottom rectangle square top and bottom two sides two sides two triangles 2 =24 + 56 + 42 = 122in =15 + 12 + 20 + 25 = 72 ft 2 A cube has a total surface area of 384 square units. What is the length of one of its edges? The surface area of a cube is 6s2 , so 6s22= 384 s = 64 s = 8 units . If the length of the side of a cube is multiplied by 4, how will the surface area of the larger cube compare to the surface area of the original cube? 2 2 2 6s is the original surface area. 6( 4ss) = 16 6 is the new surface area, so the larger cube has 16 times the original surface area. Pyramids: A pyramid is a polyhedron formed by connecting the vertices of a polygonal region called the base to another point not in the plane of the base called the apex using segments.
    [Show full text]
  • Surface Areas and Volumes
    CHAPTER 13 SURFACE AREAS AND VOLUMES (A) Main Concepts and Results • Cuboid whose length = l, breadth = b and height = h (a) Volume of cuboid = lbh (b) Total surface area of cuboid = 2 ( lb + bh + hl ) (c) Lateral surface area of cuboid = 2 h (l + b) (d) Diagonal of cuboid = lbh222++ • Cube whose edge = a (a) Volume of cube = a3 (b) Lateral Surface area = 4a2 (c) Total surface area of cube = 6a2 (d) Diagonal of cube = a 3 • Cylinder whose radius = r, height = h (a) Volume of cylinder = πr2h (b) Curved surface area of cylinder = 2πrh (c) Total surface area of cylinder = 2πr (r + h) • Cone having height = h, radius = r and slant height = l 1 (a) Volume of cone = πrh2 3 (b) Curved surface area of cone = πrl 16/04/18 122 EXEMPLAR PROBLEMS (c) Total surface area of cone = πr (l + r) (d) Slant height of cone (l) = hr22+ • Sphere whose radius = r 4 (a) Volume of sphere = πr3 3 (b) Surface area of sphere = 4πr2 • Hemisphere whose radius = r 2 (a) Volume of hemisphere = πr3 3 (b) Curved surface area of hemisphere = 2πr2 (c) Total surface area of hemisphere = 3πr2 (B) Multiple Choice Questions Write the correct answer Sample Question 1 : In a cylinder, if radius is halved and height is doubled, the volume will be (A) same (B) doubled (C) halved (D) four times Solution: Answer (C) EXERCISE 13.1 Write the correct answer in each of the following : 1. The radius of a sphere is 2r, then its volume will be 4 8πr3 32 (A) πr3 (B) 4πr3 (C) (D) πr3 3 3 3 2.
    [Show full text]
  • History of Mathematics #4 1. Before 11 Pm, Sunday, February 5. Go to The
    History of Mathematics #4 1. Before 11 pm, Sunday, February 5. Go to the Forum “Archimedes” and make at least one substantive contribution by 11 pm, Sunday, February 5, and at least one substantive response to others’ postings before class on Tuesday, February 7. Write about the following: (a) Where in the K–16 curriculum do the various results of Archimedes discussed in Dunham make their appearance? (b) Where in the K–16 curriculum do the proofs of these results make their appear- ance? (c) Do you think we should present Archimedes’ proof of the area of a circle in middle school? in high school? 2. Before Tuesday, February 7. (a) Read Dunham Chapter 4, MTA Sketch 7, and Boyer Chapter 8. If you aren’t able to to read all of Boyer, at least read the sections in Chapter 8 on The Method, Volume of a sphere, and Recovery of The Method. (b) Think about the following questions for discussion at the Centra session: i. Study Euclid’s proof by exhaustion of the volume of a circular cone (XII.10). Refer also to XII.7 and XII.5. Pretty amazing! ii. On pages 93–94 of Dunham it is asserted that the perimeter of a regular poly- gon inscribed in a circle is less than the circumference of the circle, and also that the perimeter of a regular polygon circumscribed about a circle exceeds the circumference of the circle. How might these statements be justified? iii. Try making and measuring some perimeters of inscribed and circumscribed polygons using Wingeom or Geometer’s Sketchpad.
    [Show full text]
  • Surface Area of a Sphere in This Example We Will Complete the Calculation of the Area of a Surface of Rotation
    Surface Area of a Sphere In this example we will complete the calculation of the area of a surface of rotation. If we’re going to go to the effort to complete the integral, the answer should be a nice one; one we can remember. It turns out that calculating the surface area of a sphere gives us just such an answer. We’ll think of our sphere as a surface of revolution formed by revolving a half circle of radius a about the x-axis. We’ll be integrating with respect to x, and we’ll let the bounds on our integral be x1 and x2 with −a ≤ x1 ≤ x2 ≤ a as sketched in Figure 1. x1 x2 Figure 1: Part of the surface of a sphere. Remember that in an earlier example we computed the length of an infinites­ imal segment of a circular arc of radius 1: r 1 ds = dx 1 − x2 In this example we let the radius equal a so that we can see how the surface area depends on the radius. Hence: p y = a2 − x2 −x y0 = p a2 − x2 r x2 ds = 1 + dx a2 − x2 r a2 − x2 + x2 = dx a2 − x2 r a2 = dx: 2 2 a − x The formula for the surface area indicated in Figure 1 is: Z x2 Area = 2πy ds x1 1 ds y z }| { x r Z 2 z }| { a2 p 2 2 = 2π a − x dx 2 2 x1 a − x Z x2 a p 2 2 = 2π a − x p dx 2 2 x1 a − x Z x2 = 2πa dx x1 = 2πa(x2 − x1): Special Cases When possible, we should test our results by plugging in values to see if our answer is reasonable.
    [Show full text]
  • A Brief History of Mathematics a Brief History of Mathematics
    A Brief History of Mathematics A Brief History of Mathematics What is mathematics? What do mathematicians do? A Brief History of Mathematics What is mathematics? What do mathematicians do? http://www.sfu.ca/~rpyke/presentations.html A Brief History of Mathematics • Egypt; 3000B.C. – Positional number system, base 10 – Addition, multiplication, division. Fractions. – Complicated formalism; limited algebra. – Only perfect squares (no irrational numbers). – Area of circle; (8D/9)² Æ ∏=3.1605. Volume of pyramid. A Brief History of Mathematics • Babylon; 1700‐300B.C. – Positional number system (base 60; sexagesimal) – Addition, multiplication, division. Fractions. – Solved systems of equations with many unknowns – No negative numbers. No geometry. – Squares, cubes, square roots, cube roots – Solve quadratic equations (but no quadratic formula) – Uses: Building, planning, selling, astronomy (later) A Brief History of Mathematics • Greece; 600B.C. – 600A.D. Papyrus created! – Pythagoras; mathematics as abstract concepts, properties of numbers, irrationality of √2, Pythagorean Theorem a²+b²=c², geometric areas – Zeno paradoxes; infinite sum of numbers is finite! – Constructions with ruler and compass; ‘Squaring the circle’, ‘Doubling the cube’, ‘Trisecting the angle’ – Plato; plane and solid geometry A Brief History of Mathematics • Greece; 600B.C. – 600A.D. Aristotle; mathematics and the physical world (astronomy, geography, mechanics), mathematical formalism (definitions, axioms, proofs via construction) – Euclid; Elements –13 books. Geometry,
    [Show full text]
  • Surface Area, Lateral Area, and Volume Formulas
    surfaceAreaLateralAreaVolumeFormulas 121123.odt Surface Area, Lateral Area, and Volume Formulas In the table shown B is the area of the base, P is the perimeter of the base, h is the height of the object, l is the slant height of the object, r is the radius of the base if the base is a circle, C is the circumference of the base if it is a circle, S is the surface area of the object, L is the lateral area of the object, and V is the volume of the object. Name Lateral Area Surface Area Volume Right Prism L=Ph S=2B+L or V =Bh S=2B+Ph Right Cylinder L=Ch or S=2B+L or V =Bh or = = + 2 L 2πrh S 2B Ch or V =πr h S=2πr2+2πrh Regular Pyramid 1 S=B+L or 1 L= Pl V = Bh 1 2 S= B+ Pl 3 2 = + Right Cone = 1 S B L or =1 L Cl Or V Bh or 2 S= B+πrl or 3 = = 2+ L πrl 1 2 S πr πrl V = πr h 3 = 2 Sphere 4 3 S 4πr V = πr 3 Right Prism Lateral area of a right prism: L=Ph where L is the lateral area and Ph is the product of the perimeter of one of the bases and the height of the prism. Lateral area is the surface area minus the area of the bases. The lateral area consists of only the area of the lateral faces of a prism. Surface area of a right prism: S=2B+L or S=2B+Ph where S is the total surface area, 2B is twice the area of one of the bases.
    [Show full text]