DOCSLIB.ORG

Geometric Modeling of Engineered Abrasive Processes Andres L

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometric Modeling of Engineered Abrasive Processes Andres L Rochester Institute of Technology RIT Scholar Works Articles 2005 Geometric Modeling of Engineered Abrasive Processes Andres L. Carrano Rochester Institute of Technology James B. Taylor Rochester Institute of Technology Follow this and additional works at: http://scholarworks.rit.edu/article Recommended Citation Carrano AL, Taylor JB. Geometric modeling of engineered abrasive processes. J Manuf Process 2005;7(1):17–27. https://doi.org/ 10.1016/S1526-6125(05)70078-5 This Article is brought to you for free and open access by RIT Scholar Works. It has been accepted for inclusion in Articles by an authorized administrator of RIT Scholar Works. For more information, please contact [email protected]. *Geometric Modeling of Engineered Abrasive Processes* Carrano, Andres L Abstract One of the common issues that arises in abrasive machining is the inconsistency of the surface roughness within the same batch and under identical machining conditions. Recent advances in engineered abrasives have allowed replacement of the random arrangement of minerals on conventional belts with precisely shaped structures uniformly cast directly onto a backing material. This allows for abrasive belts that are more deterministic in shape, size, distribution, orientation, and composition. A computer model based on known tooling geometry was developed to approximate the asymptotic surface profile that was achievable under specific loading conditions. Outputs included the theoretical surface parameters, R^sub q^, R^sub a^, R^sub v^, R^sub p^, R^sub t^, and R^sub sk^. Experimental validation was performed with a custom-made abrader apparatus and using engineered abrasives on highly polished aluminum samples. Interferometric microscopy was used in assessing the surface roughness. Results include the individual effects of pyramid base width, pyramid height, attack angle, and indentation depth on the surface descriptors. Introduction Some abrasives occur in nature (flint, garnet, etc.), and some are man-made (aluminum oxide, silicon carbide, zirconia, CBN, and so on). Until now, most coated abrasive tools have consisted of single or multiple layers of oriented grits of approximately the same size that are attached to a substrate. The size of the particles used on coated abrasives is established by sifting the crushed grits through screens of standard mesh (NBS), by sedimentation, or by air flotation. The application of the abrasive grits to the belt backing is either achieved through gravity or electrode-induced polarization. This traditional manufacturing practice, however, yields an abrasive belt that presents variations in grit size, shape, distribution, and orientation. Moreover, the geometry of the cutting grits changes from particle to particle, making it impossible to know, for instance, the rake or attack angle for any given grit or cut. The task of modeling the interaction of the grit and the surface of the part in an abrasive machining process has been attempted in several ways by previous researchers (Torrance 1987; Bahin 1987; Lin et al. 1996a, 1996b; Li and Liao 1997; Abede and Appl 1988; Dornfeld 1981; Buttery and Hamed 1977, 1978). The random size, shape, and relative placement of abrasive particles on the sandpaper has always presented a difficult problem to attack from a process modeling standpoint. Using statistical distributions of particle size and making assumptions about particle shape and relative placement on the substrate have allowed some researchers to estimate overall process results based on process parameters (Torrance 1987; Li and Liao 1997). This method, which is probabilistic in nature rather than deterministic, has typically served as a basis for a correlation of predicted and actual results. Another common approach to abrasive process modeling has been the single-grit approach (Abede and Appl 1988; Dornfeld 1981; Buttery and Hamed 1977; Lin et al. 1996b). This method seeks to deterministically model the interaction of a single abrasive grit and the surface of the part. Major contributions to the literature have been made via this modeling method especially with regard to the ploughing phenomenon and elastic/plastic effects (Abede and Appl 1988; Dornfeld 1981; Lin et al. 1996b; Buttery and Hamed 1978). The major shortcoming of this method is the lack of interaction of the multiple abrasive grits on the surface of the part. The actual abrasive process is the sum total of many single abrasive grits of different sizes and shapes and their effect on the surface. Recent advances in manufacturing processes have allowed replacement of the random arrangement of minerals on conventional belts by a patented technology called microreplication. The technology is a spin-off of work that was originally used in the manufacturing of reflectors. Since the original development by 3M, other companies have also produced their own engineered abrasives in similar manners (Mason 1999; Norton 2000). To date, engineered abrasives have been targeted at the much larger metals market, but interest has been shown from the wood and composites markets. As defined by 3 M (1997), microreplication is the science of creating small, precisely shaped, three-dimensional structures and reproducing them on a variety of surfaces. The belt's surface, in this case, consists of pyramidal structures containing micron-graded minerals that are uniformly applied to a backing material (see Figure 1). This development has been around for several years, but it was not until recently that commercial fabrication of belts became feasible. This new genre of abrasive tools is usually referred to as engineered or structured abrasives. They consist of abrasive belts that are more deterministic than the traditional counterpart: the shape, size, distribution, and orientation of the cutting grits are known and controlled. This provides a very even distribution of mineral and yields a more consistent rate of cut and surface finish. The motivation for pursuing such abrasives lies in the idea that, by removing variation in the grit geometry, it is possible to remove variation in the finish quality. However, a better understanding of the impact of the individual geometric features of the abrasive on the surface roughness is required as a basis for proposing an optimized geometry and for assessing the degree of performance improvement. It is believed that the future of abrasive-based machining is in microengineered belt patterns and that further job-based customization of these patterns will be a future step. Optimization of the resultant workpiece surface and machining parameters will also be possible. The main objective of this research was to develop and validate a 3-D computer-based model that would help in understanding the impact of the individual geometric features of the grit on the surface roughness of the workpiece. To date, most geometric models of abrasive processes have been developed based on a single-grit tooling supposition (Abede and Appl 1988; Dornfeld 1981; Buttery and Hamed 1977; Lin et al. 1996b; Oxley 1997), thus neglecting interactions between grits (multiple-pass effect), or consisted of theoretical approximations due to unknown geometry (Torrance 1987; Li and Liao 1997, Mulhearn and Samuels 1962). These are assumptions that simplify the models but also make them somewhat unrealistic and provide no basis for optimization. The model developed here was based on a pyramid-shaped abrasive grit, incorporated the effect of multiple passes, and was validated on commercially available products. Other literature relevant to abrasive process modeling is included for reference (Gahlin and Jacobson 1999; Komanduri 1971; Larsen-Badse 1968; Sin, Sada, and Suh 1979). Once the model was developed and validated, a second objective was to search for a better understanding of the individual geometric features and their impact on the final quality. Three main parameters were investigated: the attack angle of the belt, the pyramid width, and the pyramid height. These are the features that could potentially be changed during the manufacture of this abrasive. The other inputs to the model were: the amount of indentation (a function of the load applied), the sampling resolution (a function of the instrumentation), the number of grits/row, and the number of rows. Notice that some of these are artificial variables that arise because of the finite nature of the model (such as the number of grits and number of rows in the abrasive matrix) or variables that are not under control by the abrasive manufacturer (amount of grit indentation). Methodology The basic idea is to develop a geometric computer model that would parametrically represent the tooling and workpiece, as well as to calculate the surface descriptors that result from the interaction between these. A matrix with several grits per row and several rows, one after the other, was generated in a computer program. Because this abrasive tooling allows for perfectly known geometry, it is then possible to define the geometry as a function of base width and height of the pyramid. Rake and attack angle can be calculated from the design geometry but are also a function of the width and height. By knowing the pyramid orientation with respect to the feed direction, the offset between rows and columns of pyramids, and the depth of indentation into the workpiece (as a function of the applied pressure), it was possible to approximate the resultant 2-D surface profile after n rows of grits have performed a cut. The model assumed that the entire
Load more

Recommended publications
  • Review of Superfinishing by the Magnetic Abrasive Finishing Process
    High Speed Mach. 2017; 3:42–55 Review Article Open Access Lida Heng, Yon Jig Kim, and Sang Don Mun* Review of Superfinishing by the Magnetic Abrasive Finishing Process DOI 10.1515/hsm-2017-0004 In the conventional lapping process, loose abrasive Received May 2, 2017; accepted June 20, 2017 particles in the form of highly-concentrated slurry are of- ten used. The finishing mechanism then involves actions Abstract: Recent developments in the engineering indus- between the lapping plate, the abrasive, and the work- try have created a demand for advanced materials with su- piece, in which the abrasive particles roll freely, creating perior mechanical properties and high-quality surface fin- indentation cracks along the surface of the workpiece, ishes. Some of the conventional finishing methods such as which are then removed to finally achieve a smoother sur- lapping, grinding, honing, and polishing are now being re- face [1]. The lapping process typically is not used to change placed by non-conventional finishing processes. Magnetic the dimensional accuracy due to its very low material re- Abrasive Finishing (MAF) is a non-conventional superfin- moval rate. Grinding, on the other hand, is used to achieve ishing process in which magnetic abrasive particles inter- the surface finish and dimensional accuracy of the work- act with a magnetic field in the finishing zone to remove piece simultaneously [2]. In grinding, fixed abrasives are materials to achieve very high surface finishing and de- used by bonding them on paper or a plate for fast stock burring simultaneously. In this review paper, the working removal.
    [Show full text]
  • Big Performance
    AUGUST 2008 / VOLUME 60 / ISSUE 8 All images: Sunnen Products A motorcycle connecting rod is honed to a diameter of 1.4173", +0.0001"/-0.0003", with roundness of 0.00008", straightness of 0.00004" and cylindricity of 0.0001". Small Engines, By Rich Moellenberg, Sunnen Products Co. Big Performance Honing of cylinder bores improves sealing and component life to help small internal combustion engines increase power density and reduce exhaust emissions. changing federal regulatory climate that targets their big brothers on the NASCAR circuit, these reduced emissions and noise has led to a con- engines are also beginning to share a performance- vergence of design goals for both small internal enhancing technology used for racecar and most combustion engines and automotive engines other auto engines—honing. Honing optimizes the in the last decade. Today, small-engine OEMs cylinder bore’s geometry, surface finish and dimen- are striving for higher power densities (producing sional accuracy, boosting power density, extending more horsepower and torque from an engine with life and lowering emissions. the same physical size), lower fuel consumption and The fit between the piston and bore, along with lower emissions, all while controlling costs. the quality of the surface contact between the two, Engines for outdoor power equipment, ATVs, influences power output, combustion efficiency, snowmobiles, motorcycles and outboard motors, emissions, component life and vibration. The pre- along with many piston-type air and refrigeration cision of bore geometry (roundness, straightness, compressors, share a common operating principle— cylindricity and diameter) and surface finish play a piston reciprocates in a cylinder bore.
    [Show full text]
  • Effect of Aluminum Oxide and Silicon Carbide Abrasive Type on Stainless Steel Ground Surface Integrity
    EFFECT OF ALUMINUM OXIDE AND SILICON CARBIDE ABRASIVE TYPE ON STAINLESS STEEL GROUND SURFACE INTEGRITY MUHD SYAKIR BIN ABDUL RAHMAN Report submitted in partial fulfillment of the requirements for the award of Bachelor of Mechanical Engineering with Manufacturing Faculty of Mechanical Engineering UNIVERSITI MALAYSIA PAHANG DECEMBER 2010 ii SUPERVISOR’S DECLARATION I hereby declare that I have checked this project and in my opinion, this project is adequate in terms of scope and quality for the award of the degree of Bachelor of Mechanical Engineering. Signature: Name of Supervisor: DR. MAHADZIR BIN ISHAK @ MUHAMMAD Position: LECTURER OF MECHANICAL ENGINEERING Date: 6 DECEMBER 2010 iii STUDENT’S DECLARATION I hereby declare that the work in this report is my own except for quotations and summaries which have been duly acknowledged. The report has not been accepted for any degree and is not concurrently submitted for award of other degree. Signature: Name: MUHD SYAKIR BIN ABDUL RAHMAN ID Number: ME07013 Date: 6 DECEMBER 2010 v ACKNOWLEDGEMENTS In the name of Allah, the Most Benevolent, the Most Merciful. First of all I wish to record immeasurable gratitude and thankfulness to the One and The Almighty Creator, the Lord and Sustainers of the universe, and the Mankind in particular. It is only had mercy and help that this work could be completed and it is keenly desired that this little effort be accepted by Him to be some service to the cause of humanity. I would like to express my sincere gratitude to my supervisor DR. Mahadzir Bin Ishak @ Muhammad for his germinal ideas, invaluable guidance, continuous encouragement and constant support in making this research possible.
    [Show full text]
  • A Gentle Introduction to Abrasive (Waterjet) Machining Brought to You by the MIT Fablab Staff
    A Gentle Introduction to Abrasive (Waterjet) Machining Brought to you by the MIT FabLab Staff. In this brief two part tutorial we will give you a jump start toward making your first project parts utilizing the Department of Architecture’s new OMAX waterjet machine. In Part I we assume that you have access to a computer running the OMAX Layout software required to define new geometry or import your previously defined part geometry and then create tool paths based on this geometry. In Part II we assume that you have access to the actual waterjet machine itself, the OMAX Make software which controls the physical machine, as well as knowledgeable lab monitor or staff member who’ll be able to help with any questions or safety issues that might arise. First, a little background information about abrasive machining: The OMAX 2652 is a relatively new type of machine tool which uses a very high pressure (> 50k psi) stream of water and garnet abrasive to cut virtually any kind of material by eroding the material along an arbitrarily complex tool path that you define, leaving a thin (~0.025”), kerf. Both thin and thick materials such as aluminum, steel and stainless steel, plastics such Plexiglas and Lexan, rubber, brick and glass, and even wood may be cut on a waterjet. Material thickness can range from 1/16” through 4”, even when cutting very hard materials. Some special precautions and procedures are required for cutting brittle or very thin materials. The procedures and techniques required to use the OMAX waterjet are pretty straightforward and quick to learn.
    [Show full text]
  • UC Berkeley Consortium on Deburring and Edge Finishing
    UC Berkeley Consortium on Deburring and Edge Finishing Title Advancing Cutting Technology Permalink https://escholarship.org/uc/item/7hd8r1ft Authors Byrne, G. Dornfeld, David Denkena, B. Publication Date 2003 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Advancing Cutting Technology G. Byrne1 (1), D. Dornfeld2 (1), B. Denkena3 1 University College Dublin, Ireland 2 University of California, Berkeley, USA 3 University of Hannover, Germany Abstract This paper reviews some of the main developments in cutting technology since the foundation of CIRP over fifty years ago. Material removal processes can take place at considerably higher performance levels 3 in the range up to Qw = 150 - 1500 cm /min for most workpiece materials at cutting speeds up to some 8.000 m/min. Dry or near dry cutting is finding widespread application. The superhard cutting tool materi- als embody hardness levels in the range 3000 – 9000 HV with toughness levels exceeding 1000 MPa. Coated tool materials offer the opportunity to fine tune the cutting tool to the material being machined. Machining accuracies down to 10 µm can now be achieved for conventional cutting processes with CNC machine tools, whilst ultraprecision cutting can operate in the range < 0.1µm. The main technological developments associated with the cutting tool and tool materials, the workpiece materials, the machine tool, the process conditions and the manufacturing environment which have led to this advancement are given detailed consideration in this paper. The basis for a roadmap of future development of cutting tech- nology is provided. Keywords: Cutting, Material Removal, Process Development ACKNOWLEDGEMENTS geometrie”.
    [Show full text]
  • Grinding and Other Abrasive Processes
    GRINDING AND OTHER ABRASIVE PROCESSES •Grinding •Related Abrasive Process ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” Abrasive Machining Material removal by action of hard, abrasive particles usually in the form of a bonded wheel •Generally used as finishing operations after part geometry has been established y conventional machining •Grinding is most important abrasive processes •Other abrasive processes: honing, lapping, superfinishing, polishing, and buffing ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” Why Abrasive Processes are Important •Can be used on all types of materials •Some can produce extremely fine surface finishes, to 0.025 m (1 -in) •Some can hold dimensions to extremely close tolerances ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” Grinding Material removal process in which abrasive particles are contained in a bonded grinding wheel that operates at very high surface speeds •Grinding wheel usually disk-shaped and precisely balanced for high rotational speeds ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” The Grinding Wheel •Consists of abrasive particles and bonding material Abrasive particles accomplish cutting Bonding material holds particles in place and establishes shape and structure of wheel ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” Grinding Wheel Parameters •Abrasive material •Grain size •Bonding material •Wheel grade •Wheel structure ©2002 John Wiley & Sons, Inc. M. P. Groover, “Fundamentals of Modern Manufacturing 2/e” Abrasive Material Properties •High hardness •Wear resistance •Toughness •Friability - capacity to fracture when cutting edge dulls, so a new sharp edge is exposed ©2002 John Wiley & Sons, Inc.
    [Show full text]
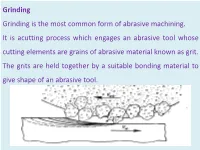
  • Grinding Grinding Is the Most Common Form of Abrasive Machining. It Is Acutting Process Which Engages an Abrasive Tool Whose
    Grinding Grinding is the most common form of abrasive machining. It is acutting process which engages an abrasive tool whose cutting elements are grains of abrasive material known as grit. The grits are held together by a suitable bonding material to give shape of an abrasive tool. Advantages of grinding • dimensional accuracy • good surface finish • good form and locational accuracy • applicable to both hardened and unhardened material. Applications of grinding •surface finishing • slitting and parting • descaling, deburring • stock removal (abrasive milling) • finishing of flat as well as cylindrical surface • grinding of tools and cutters and resharpening of the same . Conventional grinding machines are classified as: (a) Surface grinding machine (b) Cylindrical grinding machine (c) Internal grinding machine (d) Tool and cutter grinding machine a)Surface grinding machine: This machine may be similar to a milling machine used mainly to grind flat surface. However, some types of surface grinders are also capable of producing contour surface with formed grinding wheel. Basically there are four different types of surface grinding machines characterised by the movement of their tables and the orientation of grinding wheel spindles as follows: • Horizontal spindle and reciprocating table • Vertical spindle and reciprocating table • Horizontal spindle and rotary table • Vertical spindle and rotary table B)Cylindrical grinding machine This machine is used to produce external cylindrical surface. The surfaces may be straight, tapered, steps or profiled. Broadly there are three different types of cylindrical grinding machine as follows: 1. Plain centre type cylindrical grinder 2. Universal cylindrical surface grinder 3. Centreless cylindrical surface grinder Plain centre type cylindrical grinder Universal cylindrical surface grinder Centreless grinder C)Internal grinding machine This machine is used to produce internal cylindrical surface.
    [Show full text]
  • New Highly Efficient Methods of Machining Metals
    Ye. Dlugash, Junior specialist student T. Rishan, teacher of technology of machine-building, research advisor N. Barbelko, PhD in Pedagogy, language advisor Berdychiv College of Industry, Economics and Law NEW HIGHLY EFFICIENT METHODS OF MACHINING METALS The requirements to quality and reliability of mechanical parts are constantly increased. New highly efficient methods of machining metals are used for increasing the firmness of details to the wear, resistance to corrosion to the action of aggressive substances and improvement of other operating indexes. These machining methods have already found wide application in a modern engineering, such as the electrophysical and electrochemical machining methods. This article deals with such new highly efficient machining methods of metals as electrical discharge, ultrasonic, beam and electrochemical machining methods. Main advantages of these methods are: possibility of machining of difficult form parts with playback of instrument form; a capacity to treat of materials of any hardness and viscosity; possibility of machining of the curvilinear and spiral holes, producing of the very small holes, narrow and deep slots; absence of distortions of materials structures; possibility to use of instruments, which made of less durable materials than workpiece; an increasing of the labour productivity and simplification of equipment during treatment of especially difficult parts. All types of electrophysical and electrochemical machining methods can be divided into such categories: electrical discharge, electrochemical, ultrasonic, electron beam and combined. In all these methods of machining removal of assumption is made due to electric or chemical erosion. The general disadvantage of these machining methods is a substantial increasing of energy intensity of processes.
    [Show full text]
  • ABSTRACT Kametz, David Austin. Precision Fabrication and Development of Charging and Testing Methods of Fixed-Abrasive Lapping P
    ABSTRACT Kametz, David Austin. Precision Fabrication and Development of Charging and Testing Methods of Fixed-Abrasive Lapping Plates. (Under the direction of Dr. Thomas A. Dow.) The recording head industry is one of the dominant users of advanced ceramics such as alumina, silicon nitride, silicon carbide and AlTiC. The high hardness of these materials makes diamond the optimal abrasive for machining. One challenge when manufacturing recording heads for rigid disk drives is to generate surfaces that are both planar and smooth. Flatness tolerances are in the range of a few tens of nanometers to a few hundred nanometers per millimeter of length [1]. Roughness tolerances are in the range of a few nanometers to the subnanometer range [1]. Fixed-abrasive lapping, sometimes called nanogrinding, is a common method of machining used on ceramics. Fixed- abrasive lapping is generally a two-body abrasive process, with the abrasive grain fixed in the lapping plate that produces an extremely smooth surface due to the controlled depth of cut. The process of fabricating a quality fixed-abrasive lapping plate is a lengthy and sometimes demanding process. The goals of this research are to investigate the current fabrication process for improvements in surface texture quality, charging time and waste reduction of abrasive as well as the development of methods and equipment capable of estimating the lapping qualities of the plate during it’s fabrication process. The improvement of this process will reduce plate fabrication time and improve lapping performance. Current processes used to fabricate a plate can require 2 hours or more, and often the lapping quality of the plate is unknown until it is used.
    [Show full text]
  • Elimination of Honing Stick Mark in Rack Tube B.Parthiban11, N.Arul Kumar2, K.Gowtham Kumar3, P.Karthic4, R.Logesh Kumar5 Assistant Professor, Dept
    ISSN(Online) : 2319-8753 ISSN (Print) : 2347-6710 International Journal of Innovative Research in Science, Engineering and Technology (An ISO 3297: 2007 Certified Organization) Website: www.ijirset.com Vol. 6, Issue 3, March 2017 Elimination of Honing Stick Mark in Rack Tube B.Parthiban11, N.Arul Kumar2, K.Gowtham Kumar3, P.Karthic4, R.Logesh Kumar5 Assistant Professor, Dept. of Mechanical Engineering, Jay Shriram Group of Institutions. Tiruppur, Tamilnadu, India UG Student, Dept. of Mechanical Engineering, Jay Shriram Group of Institutions. Tiruppur, Tamilnadu, India.2,3,4,5 ABSTRACT: The main objective of the project is to reduce the tool tip mark produced during honing process in rack tube manufacturing. Rack tube is used in power steering, the hydraulic fluid acts inside the cylinder walls. Honing is an internal finishing process that uses abrasive particles on a rotating tool to produce extremely accurate dimensions and smooth surface finish. Similar to grinding and lapping process the abrasive particles are mounted on the rotating tool. During machining process tool have the working motion (both rotating and reciprocating motion). Work piece does not perform any motion. By the application of pressure acting on the tool, the tip marks are produced inside the work piece. To overcome this draw back. By changing the grain size of the hone stone the tool tip mark has been reduced and productivity increased KEYWORDS: honing machine, stick mark, spindle, abrasive stick I. INTRODUCTION Honing is an internal finishing process that uses abrasives on a rotating tool to produce extremely accurate holes that require a very smooth finish. Honing is a low velocity abrasive machining process in which a tool called hone carries out a combined rotary and reciprocating motion.
    [Show full text]
  • Mechanical Performance of Abrasive Sandpaper Made with Palm Kernel
    Journal of the Mechanical Behavior of Materials 2021; 30:28–37 Research Article Hameed Sa’ad, Bamidele D. Omoleyomi, Elijah A. Alhassan*, Ezekiel O. Ariyo, and Taiwo Abadunmi Mechanical performance of abrasive sandpaper made with palm kernel shells and coconut shells https://doi.org/10.1515/jmbm-2021-0004 Received Oct 07, 2020; accepted Mar 01, 2021 1 Introduction Abstract: The use of agricultural wastes as additives for An increase in population coupled with a corresponding other valuable products has been the focus of many re- increase in demand for agricultural products has resulted search efforts because of their availability, inherent prop- in enormous generations of agricultural wastes that pose erties, and environmental friendliness. Palm kernel shells a challenge to farmers in terms of their proper handling, (PKS) and coconut shells (CNS) are agricultural solid end management, and disposal. Most often in Nigeria’s farm- products obtainable from the cracking of their fruit nuts. ing perspective, these wastes have near-zero commercial In this study, PKS and CNS were used to produce abrasive or economic usage hence constituting a menace to the en- sandpaper following established procedures. The mechani- vironment [1]. Their alternative utilization as raw materi- cal properties of the sandpaper produced were established. als for other valuable products has recently gained atten- Material for application in abrasive operations must exhibit tion among researchers. Hence, an increased interest in maximum hardness and compressive strength, minimal the effective and efficient ways of appropriating agricul- wear rate, water absorption, and density. Results showed a tural wastes as an alternative source of raw materials [2, 3].
    [Show full text]
  • Abrasive Machining and Finishing Operations
    Abrasive Machining and Finishing Operations Manufacturing, Engineering & Technology, Fifth Edition, by Serope Kalpakjian and Steven R. Schmid. ISBN 0-13-148965-8. © 2006 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. Bonded Abrasives Used in Abrasive-Machining Processes Figure 25.1 A variety of bonded abrasives used in abrasive- machining processes. Source: Courtesy of Norton Company. Manufacturing, Engineering & Technology, Fifth Edition, by Serope Kalpakjian and Steven R. Schmid. ISBN 0-13-148965-8. © 2006 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. Workpieces and Operations Used in Grinding Figure 26.2 The types of workpieces and operations typical of grinding: (a) cylindrical surfaces, (b) conical surfaces. (c) fillets on a shaft, (d) helical profiles, (e) concave shape, (f) cutting off or slotting with thin wheels, and (g) internal grinding. Manufacturing, Engineering & Technology, Fifth Edition, by Serope Kalpakjian and Steven R. Schmid. ISBN 0-13-148965-8. © 2006 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. Ranges of Knoop Hardness for Various Materials and Abrasives Manufacturing, Engineering & Technology, Fifth Edition, by Serope Kalpakjian and Steven R. Schmid. ISBN 0-13-148965-8. © 2006 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. Grinding Wheel Model Figure 26.3 Schematic illustration of a physical model of a grinding wheel showing its structure and wear and fracture patterns. Manufacturing, Engineering & Technology, Fifth Edition, by Serope Kalpakjian and Steven R. Schmid. ISBN 0-13-148965-8. © 2006 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. Grinding Wheels Figure 26.4 Common types of grinding wheels made with conventional abrasives.
    [Show full text]