DOCSLIB.ORG

Introduction to Isogeometric Elements G in LS-DYNA

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction to Isogeometric Elements G in LS-DYNA Introduction to Isogeometric Elements in LS-DYNA T.J.R. Hughes Entwicklerforum October 12th, 2011, Stuttgart, Germany Stefan Hartmann Development in cooperation with: D.J. Benson: Professor of Applied Mechanics, University of California, San Diego, USA Some slides borrowed from: T.J.R. Hughes: Professor of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin, USA 1 Outline Isogeometric Analysis - motivation / definition / history From B-splines to NURBS (T.J.R. Hughes) - basis functions / control net / refinements NURBS-based finite elements in LS-DYNA -*ELEMENT_NURBS _PATCH _2D Example 1: Square Tube Buckling - description / deformation Example 2: Underbody Cross Member (Numisheet 2005) - diti/description / compar ison o f resu lt/lts / summary Summary and Outlook Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 2 Isogeometric Analysis – motivation & definition reduce effort of geometry conversion from CAD into a suitable mesh for FEA ISOPARAMETRIC (FE-Analysis) use same approximation for geometry and deformation (normally: low order Lagrange polynomials ---- in LS-DYNA basically only linear elements) GEOMETRY DEFORMATION ISOGEOMETRIC (CAD - FEA) same description of the geometry in the design (CAD) and the analysis (FEA) CAD FEA common geometry descriptions in CAD - NURBS (Non-Uniform Rational B-splines) most commonly used - T-splines enhancement of NURBS - subdivision surfaces mainly used in animation industry -andthd others Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 3 Isogeometric Analysis -history start in 2003 - summer: Austin Cotrell starts as PhD Student of Prof. T.J.R. Hughes at the University of Texas, Austin - autumn: first NURBS-based FE-code for linear, static problems provides promising results, the name „ISOGEOMETRIC“ is used the first time 2004 up to now: many research activities to various topics - non-linear structural mechanics shells with and without rotational DOFs implicit gradient enhanced damage XFEM - shape- und topology-optimization - efficient numerical integration - turbulence and fluid-structure-interaction - acoustics - refinement strategies -… January 2011: first thematic conference on Isogeometric Analysis -“Isogeometric Analysis 2011: Integrating Integrating Design and Analysis “, University of Texas at Austin Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 4 From B-splines to NURBS B-spline basis functions - constructed recursively - ppy(ggpy)ositive everywhere (in contrast to Lagrange polynomials) - shape of basis functions depend on: knot-vector and polynomial degree - knot-vector: non-decreasing set of coordinates in parameter space - normally C(P-1)-continuity e.ggq. lin. / quad. / cub. / quart. La gggrange: C0 / C0 / C0 / C0 e.g. lin. / quad. / cub. / quart. B-spline: C0 / C1 / C2 / C3 Example of a uniform knot -vector: p 0: p=0 1 if ii1 Ni,0 0 otherwise p=1 p 0: ip1 NN i N ip, ip,1 i 1,1 p ip i ip11 i p=2 T.J.R. Hughes Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 5 From B-splines to NURBS B-spline curves - control points Bi / control polygon (control net) - knots linear combination: n CB Nip, i i1 T.J.R. Hughes Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 6 From B-splines to NURBS NURBS – Non-Uniform Rational B-splines - weights at control points leads to more control over the shape of a curve - ppjrojective transformation of a B-spline weight 9=09=19=29=59=10 Nw p ip, i 9 Ri W 8 n with: W Nip, w i i1 n 3 p CB Rii 7 i1 2 4 10 1 5 6 11 13 0 12 Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 7 From B-splines to NURBS Smoothness of Lagrange polynomials vs. NURBS T.J.R. Hughes Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 8 From B-splines to NURBS NURBS – surfaces (tensor-product of univariate basis) p,q NMwijiji,,,p j q ij Rij, , W , nm with:, W Nip,,, M jq w ij ij11 T.J.R. Hughes Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 9 From B-splines to NURBS - summary B-spline basis functions - recursive - dependent on knot -vector and polynomial order - normally C(P-1)-continuity - „partition of unity“ (like Lagrange polynomials) - refinement (h/p and k) without changing the initial geometry adaptivity - control points are normally not a part of the physical geometry (non-interpolatory basis functions) NURBS - B-spline basis functions + control net with weights - all mentioned properties for B-splines apply for NURBS Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 10 NURBS-based finite elements in LS-DYNA A typical NURBS-Patch and the definition of elements - elements are defined through the knot-vectors (interval between different values) - shape functions for each control-point z polynomial order: - quadratic in r-direction (pr=2) y - quadtiidratic in s-direc tion (ps= 2) x s M 3 s 5 M 4 2 r NURBS-Patch ,2,3,3,3] M3 1 (physical space) M2 M1 0 r 0 1 2 ot=[0,0,0,1 CtlControl-PitPoints nn N1 N4 N2 N3 sk Control-Net NURBS-Patch rknot=[0,0,0,1,2,2,2] „Finite Element“ (parameter space) Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 11 NURBS-based finite elements in LS-DYNA A typical NURBS-Patch – Connectivity of elements - Possible „overlaps“ ( higher continuity!) NURBS-Patch - Size of „overlap“ depends on polynomial order (and on knot-vector) (parameter space) s M5 3 M 4 2 M3 1 M2 M 1 0 r 0 1 2 N1 N4 N2 N3 Control-Points NURBS-Patch Control-Net (h(phys ica l space ) „Finite Element“ Connectivity of „FiFinitenit e ElElement“ement“ Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 12 NURBS-based finite elements in LS-DYNA New Keyword: *ELEMENT_NURBS_PATCH_2D - definition of NURBS-surfaces - 4 different shell formulations with/without rotational DOFs Pre- and Postprocessing - work in ppgrogress for LS-PrePost … current status ((pplspp3.2beta) visualization of 2D-NURBS-Patches import IGES-format and construct *ELEMENT_NURBS_PATCH_2D modification of 2D-NURBS geometry … much more to come! Postprocessing and boundary conditions (i.e. contact) currently with - interpp(y)olation nodes (automatically created) - interpolation elements (automatically created) Analysis capabilities - implicit and explicit time integration - eigenvalue analysis - other capabilities (e.g. geometric stiffness for buckling) implemented but not yet tested LS-DYNA material library available (including umats) Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 13 NURBS-based finite elements in LS-DYNA *ELEMENT_NURBS_PATCH_2D $---+--EID----+--PID----+--NPR----+---PR----+--NPS----+---PS----+----7----+----8 11 12 4 2 5 2 $---+--WFL----+-FORM----+--INT----+-NISR----+-NISS----+IMASS----+----7----+----8 0 0 1 2 2 0 $rk-+----1----+----2----+----3----+----4----+----5----+----6----+----7----+----8 0.0 0.0 0.0 1.0 2.0 2.0 2.0 $sk-+----1----+----2----+----3----+----4----+----5----+----6----+----7----+----8 0.0 0.0 0.0 1.0 2.0 3.0 3.0 3.0 $net+---N1----+---N2----+---N3----+---N4----+---N5----+---N6----+---N7----+---N8 1 2 3 4 5 6 7 8 91011129 10 11 12 13 14 15 16 18 17 18 19 20 14 19 17 13 15 20 10 16 9 11 Control Points 12 5 6 Control Net s 7 r 2 z 3 8 1 y x 4 Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 14 NURBS-based finite elements in LS-DYNA ... $---+--WFL----+-FORM----+--INT----+-NISR----+-NISS----+IMASS 0 0 1 220 NISR/NISS – Number of Interpolation Elements per Nurbs-Element (r-/s-dir.) important for post-processing, boundary conditions and contact treatment 18 automatically created: 14 19 z 17 Nurbs-Element y 13 15 Interpolation Node x 20 10 16 Interpolation Element 9 11 12 5 6 s 7 r 2 3 8 1 input: Control Points 4 Control Net Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 15 NURBS-based finite elements in LS-DYNA LSPP: Preppgrocessing LSPP: Postppgrocessing - control-net - Interpolation nodes/elements - nurbs surface nisr=niss=2 nisr=niss=10 Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 16 Square Tube Buckling – Description standard benchmark for automobile crashworthiness quarter symmetry to reduce cost perturbation to initiate buckling mode J2 plasticity with linear isotropic hardening mesh: - 640 quartic (P=4) elements - 1156 control points - 3 integration points through thickness D.J. Benson Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 17 Square Tube Buckling D.J. Benson Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 18 Square Tube Buckling D.J. Benson Introduction to Isogeometric Elements in LS-DYNA Entwicklerforum, October 12th, 2011, Stuttgart, Germany 19 Underbody Cross Member – Description Z X Upper die (rigid) Y Binder (rigid) Blank 1.6mm Lower punch (rigid) Tool moving directions Radius of Drawbead - Lower punch: stationary about 4mm - UdiUpper
Load more

Recommended publications
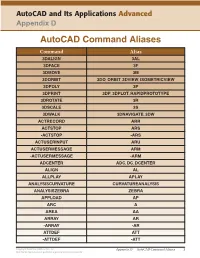
  • Autocad Command Aliases
    AutoCAD and Its Applications Advanced Appendix D AutoCAD Command Aliases Command Alias 3DALIGN 3AL 3DFACE 3F 3DMOVE 3M 3DORBIT 3DO, ORBIT, 3DVIEW, ISOMETRICVIEW 3DPOLY 3P 3DPRINT 3DP, 3DPLOT, RAPIDPROTOTYPE 3DROTATE 3R 3DSCALE 3S 3DWALK 3DNAVIGATE, 3DW ACTRECORD ARR ACTSTOP ARS -ACTSTOP -ARS ACTUSERINPUT ARU ACTUSERMESSAGE ARM -ACTUSERMESSAGE -ARM ADCENTER ADC, DC, DCENTER ALIGN AL ALLPLAY APLAY ANALYSISCURVATURE CURVATUREANALYSIS ANALYSISZEBRA ZEBRA APPLOAD AP ARC A AREA AA ARRAY AR -ARRAY -AR ATTDEF ATT -ATTDEF -ATT Copyright Goodheart-Willcox Co., Inc. Appendix D — AutoCAD Command Aliases 1 May not be reproduced or posted to a publicly accessible website. Command Alias ATTEDIT ATE -ATTEDIT -ATE, ATTE ATTIPEDIT ATI BACTION AC BCLOSE BC BCPARAMETER CPARAM BEDIT BE BLOCK B -BLOCK -B BOUNDARY BO -BOUNDARY -BO BPARAMETER PARAM BREAK BR BSAVE BS BVSTATE BVS CAMERA CAM CHAMFER CHA CHANGE -CH CHECKSTANDARDS CHK CIRCLE C COLOR COL, COLOUR COMMANDLINE CLI CONSTRAINTBAR CBAR CONSTRAINTSETTINGS CSETTINGS COPY CO, CP CTABLESTYLE CT CVADD INSERTCONTROLPOINT CVHIDE POINTOFF CVREBUILD REBUILD CVREMOVE REMOVECONTROLPOINT CVSHOW POINTON Copyright Goodheart-Willcox Co., Inc. Appendix D — AutoCAD Command Aliases 2 May not be reproduced or posted to a publicly accessible website. Command Alias CYLINDER CYL DATAEXTRACTION DX DATALINK DL DATALINKUPDATE DLU DBCONNECT DBC, DATABASE, DATASOURCE DDGRIPS GR DELCONSTRAINT DELCON DIMALIGNED DAL, DIMALI DIMANGULAR DAN, DIMANG DIMARC DAR DIMBASELINE DBA, DIMBASE DIMCENTER DCE DIMCONSTRAINT DCON DIMCONTINUE DCO, DIMCONT DIMDIAMETER DDI, DIMDIA DIMDISASSOCIATE DDA DIMEDIT DED, DIMED DIMJOGGED DJO, JOG DIMJOGLINE DJL DIMLINEAR DIMLIN, DLI DIMORDINATE DOR, DIMORD DIMOVERRIDE DOV, DIMOVER DIMRADIUS DIMRAD, DRA DIMREASSOCIATE DRE DIMSTYLE D, DIMSTY, DST DIMTEDIT DIMTED DIST DI, LENGTH DIVIDE DIV DONUT DO DRAWINGRECOVERY DRM DRAWORDER DR Copyright Goodheart-Willcox Co., Inc.
    [Show full text]
  • Tortoisemerge a Diff/Merge Tool for Windows Version 1.11
    TortoiseMerge A diff/merge tool for Windows Version 1.11 Stefan Küng Lübbe Onken Simon Large TortoiseMerge: A diff/merge tool for Windows: Version 1.11 by Stefan Küng, Lübbe Onken, and Simon Large Publication date 2018/09/22 18:28:22 (r28377) Table of Contents Preface ........................................................................................................................................ vi 1. TortoiseMerge is free! ....................................................................................................... vi 2. Acknowledgments ............................................................................................................. vi 1. Introduction .............................................................................................................................. 1 1.1. Overview ....................................................................................................................... 1 1.2. TortoiseMerge's History .................................................................................................... 1 2. Basic Concepts .......................................................................................................................... 3 2.1. Viewing and Merging Differences ...................................................................................... 3 2.2. Editing Conflicts ............................................................................................................. 3 2.3. Applying Patches ...........................................................................................................
    [Show full text]
  • Homotopical Patch Theory (Expanded Version)
    Homotopical Patch Theory (Expanded Version) Carlo Angiuli ∗ Edward Morehouse ∗ Daniel R. Licata Carnegie Mellon University Carnegie Mellon University Wesleyan University [email protected] [email protected] [email protected] Robert Harper ∗ Carnegie Mellon University [email protected] Abstract In homotopy theory, one studies topological spaces by way of their Homotopy type theory is an extension of Martin-Löf type theory, points, paths (between points), homotopies (paths or continuous de- based on a correspondence with homotopy theory and higher cat- formations between paths), homotopies between homotopies (paths egory theory. In homotopy type theory, the propositional equality between paths between paths), and so on. In type theory, a space type becomes proof-relevant, and corresponds to paths in a space. corresponds to a type A. Points of a space correspond to elements This allows for a new class of datatypes, called higher inductive a; b : A. Paths in a space are represented by elements of the identity types, which are specified by constructors not only for points but type (propositional equality), which we notate p : a =A b. Homo- also for paths. In this paper, we consider a programming application topies between paths p and q correspond to elements of the iterated identity type p = q. The rules for the identity type allow one of higher inductive types. Version control systems such as Darcs are a=Ab based on the notion of patches—syntactic representations of edits to define the operations on paths that are considered in homotopy to a repository. We show how patch theory can be developed in ho- theory.
    [Show full text]
  • U S P I M S B C S Improving Parallelism in Git-Grep Matheus
    University of São Paulo Institute of Mathematics and Statistics Bachelor of Computer Science Improving Parallelism in git-grep Matheus Tavares Bernardino Final Essay [v2.0] mac 499 - Capstone Project Program: Computer Science Advisor: Prof. Dr. Alfredo Goldman São Paulo January 19, 2020 Abstract Matheus Tavares Bernardino. Improving Parallelism in git-grep. Capstone Project Report (Bachelor). Institute of Mathematics and Statistics, University of São Paulo, São Paulo, 2019. Version control systems have become standard use in medium to large software development. And, among them, Git has become the most popular (Stack Exchange, Inc., 2018). Being used to manage a large variety of projects, with dierent magnitudes (in both content and history sizes), it must be build to scale. With this in mind, Git’s grep command was made parallel using a producer-consumer mechanism. However, when operating in Git’s internal object store (e.g. for a search in older revisions), the multithreaded version became slower than the sequential code. For this reason, threads were disabled in the object store case. The present work aims to contribute to the Git project improving the parallelization of the grep command and re-enabling threads for all cases. Analyzes were made on git-grep to locate its hotspots, i.e. where it was consumming the most time, and investigate how that could be mitigated. Between other ndings, these studies showed that the object decompression rou- tines accounted for up to one third of git-grep’s total execution time. These routines, despite being thread-safe, had to be serialized in the rst threaded implementation, because of the surrouding thread-unsafe object reading machinery.
    [Show full text]
  • Oracle Goldengate for Windows and UNIX
    Oracle® GoldenGate Windows and UNIX Administrator’s Guide 11g Release 2 Patch Set 1 (11.2.1.0.1) E29397-01 April 2012 Oracle GoldenGate Windows and UNIX Administrator’s Guide 11g Release 2 Patch Set 1 (11.2.1.0.1) E29397-01 Copyright © 2012, Oracle and/or its affiliates. All rights reserved. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, the following notice is applicable: U.S. GOVERNMENT RIGHTS Programs, software, databases, and related documentation and technical data delivered to U.S. Government customers are "commercial computer software" or "commercial technical data" pursuant to the applicable Federal Acquisition Regulation and agency-specific supplemental regulations. As such, the use, duplication, disclosure, modification, and adaptation shall be subject to the restrictions and license terms set forth in the applicable Government contract, and, to the extent applicable by the terms of the Government contract, the additional rights set forth in FAR 52.227-19, Commercial Computer Software License (December 2007).
    [Show full text]
  • IBM Tivoli Endpoint Manager for Patch Management Continuous Patch Compliance Visibility and Enforcement
    IBM Software Data Sheet Tivoli IBM Tivoli Endpoint Manager for Patch Management Continuous patch compliance visibility and enforcement With software and the threats against that software constantly evolving, Highlights organizations need an effective way to assess, deploy and manage a con- stant flow of patches for the myriad operating systems and applications in ● Automatically manage patches for multi- their heterogeneous environments. For system administrators responsible ple operating systems and applications across hundreds of thousands of end- for potentially tens or hundreds of thousands of endpoints running vari- points regardless of location, connection ous operating systems and software applications, patch management type or status can easily overwhelm already strained budgets and staff. IBM Tivoli® ● Reduce security and compliance risk by Endpoint Manager for Patch Management balances the need for fast slashing remediation cycles from weeks deployment and high availability with an automated, simplified patching to days or hours process that is administered from a single console. ● Gain greater visibility into patch compli- ance with flexible, real-time monitoring Tivoli Endpoint Manager for Patch Management, built on BigFix® and reporting technology, gives organizations access to comprehensive capabilities ● Provide up-to-date visibility and control for delivering patches for Microsoft® Windows®, UNIX®, Linux® and from a single management console Mac operating systems, third-party applications from vendors including Adobe®, Mozilla, Apple and Java™, and customer-supplied patches to endpoints—regardless of their location, connection type or status. Endpoints can include servers, laptops, desktops, and specialized equip- ment such as point-of-sale (POS) devices, ATMs, and self-service kiosks. Apply only the correct patches to the correct endpoint One approach to patch management is to create large patch files with a large update “payload” and distribute them to all of the endpoints, regardless of whether they already have all of the patches or not.
    [Show full text]
  • Controlling CEMLI 10154
    Session ID: Controlling CEMLI 10154 Prepared by: Michael Brown Applications DBA A Code Migration Methodology BlueStar @MichaelBrownOrg Remember to complete your evaluation for this session within the app! Who Am I • Over 22 years experience with Oracle Database • Over 18 years experience with E-Business Suite • Chair, OAUG Database SIG • Co-Founder AppsPerf • Oracle ACE • OAUG Member of the Year 2013 • Applications DBA, BlueStar What • What are customizations? – R12.2 • Migration flow Customizations CEMLI • Definition – Configuration – Extensions – Modification – Localization – Integration CEMLI • Definition – Configuration – Extensions – Modification – Localization – Integration • Simpler – Changes made to the application outside of the applications • Not setups • Not personalizations • Potentially completely separate, e.g. Applications Express 12.2 • Standards are now requirements • Patch Cycle • If custom application server applications are used (including Applications Express), you must use a separate application server • Rest of presentation will assume 12.2 since the requirements are a superset of previous releases. Migration Flow Migration Flow • Minimum of two instances prior to production. Development Migration Flow • Minimum of two instances prior to production. Development Test Migration Flow • Minimum of two instances prior to production. Development Test Production Migration Flow R&D, Patch, etc. Development Test Production Development Production Two Support How do we control the migrations • Various tools exist, but they are expensive • What can we do with what we have – FNDLOAD – XDOLoader – scripting A Manual Methodology Migration Template • All migrations are in the same place – Environment variable $MIGRATE • Pre 12.2, actually under custom_top • 12.2, Outside of 12.2 Filesystems – /u01/app/oracle/apps/fs1 – /u01/app/oracle/apps/fs2 – /u01/app/oracle/apps/fs_ne – /u01/app/oracle/apps/migrate • Cloning • Each migration is put into a single directory – Naming convention: Development_Instance-#, e.g.
    [Show full text]
  • Installing the Watson Knowledge Catalog Service Patch 3.0.0.2 on IBM Cloud Pak for Data 2.5
    Installing the Watson Knowledge Catalog service patch 3.0.0.2 on IBM Cloud Pak for Data 2.5 Contents Overview ...................................................................................................................................................... 3 Installing the patch .................................................................................................................................... 3 Post-installation steps .............................................................................................................................. 4 Overview This service patch contains defect fixes and supports migration of data from IBM InfoSphere Information Server 11.7.1 to IBM Cloud Pak for Data 2.5.0. These instructions assume that you have the following products already installed in your Red Hat OpenShift cluster: - IBM® Cloud Pak for Data. For more information, see Installing Cloud Pak for Data on a Red Hat OpenShift cluster. - Watson Knowledge Catalog. For more information, see Installing the Watson Knowledge Catalog service. Required role: To install the patch, you must be a cluster administrator. Installing the patch To install the Watson Knowledge Catalog service patch 3.0.0.2, complete the following steps: 1. The patch files are publicly available in the IBM Cloud Pak GitHub repository. Make sure that the repo.yaml file that defines your registries and file servers contains reference to this URL: https://raw.githubusercontent.com/IBM/cloud-pak/master/repo/cpd 2. Change to the directory for the Cloud Pak for
    [Show full text]
  • Git Patch Operation
    GGIITT -- PPAATTCCHH OOPPEERRAATTIIOONN http://www.tutorialspoint.com/git/git_patch_operation.htm Copyright © tutorialspoint.com Patch is a text file, whose contents are similar to Git diff, but along with code, it also has metadata about commits; e.g., commit ID, date, commit message, etc. We can create a patch from commits and other people can apply them to their repository. Jerry implements the strcat function for his project. Jerry can create a path of his code and send it to Tom. Then, he can apply the received patch to his code. Jerry uses the Git format-patch command to create a patch for the latest commit. If you want to create a patch for a specific commit, then use COMMIT_ID with the format-patch command. [jerry@CentOS project]$ pwd /home/jerry/jerry_repo/project/src [jerry@CentOS src]$ git status -s M string_operations.c ?? string_operations [jerry@CentOS src]$ git add string_operations.c [jerry@CentOS src]$ git commit -m "Added my_strcat function" [master b4c7f09] Added my_strcat function 1 files changed, 13 insertions(+), 0 deletions(-) [jerry@CentOS src]$ git format-patch -1 0001-Added-my_strcat-function.patch The above command creates .patch files inside the current working directory. Tom can use this patch to modify his files. Git provides two commands to apply patches git amand git apply, respectively. Git apply modifies the local files without creating commit, while git am modifies the file and creates commit as well. To apply patch and create commit, use the following command: [tom@CentOS src]$ pwd /home/tom/top_repo/project/src [tom@CentOS src]$ git diff [tom@CentOS src]$ git status –s [tom@CentOS src]$ git apply 0001-Added-my_strcat-function.patch [tom@CentOS src]$ git status -s M string_operations.c ?? 0001-Added-my_strcat-function.patch The patch gets applied successfully, now we can view the modifications by using the git diff command.
    [Show full text]
  • Host Security: Pop Ups and Patch Management
    Host Security: Pop Ups and Patch Management Table of Contents Pop-ups ........................................................................................................................................... 2 Pop-up Blockers -1 .......................................................................................................................... 3 Pop-up Blockers -2 .......................................................................................................................... 5 Patch Management ......................................................................................................................... 7 Application Patch Management ................................................................................................... 12 Patch Management ....................................................................................................................... 14 Approved Application List ............................................................................................................. 15 Hardware Security ........................................................................................................................ 17 Notices .......................................................................................................................................... 18 Page 1 of 18 Pop-ups Pop-ups Pop-ups (and popunders) refer to a class of images which appear on a user’s screen without the user performing any action to deliberately invoke their appearance. • Pop-ups are not directly
    [Show full text]
  • Coordinated Concurrent Programming in Syndicate
    Coordinated Concurrent Programming in Syndicate Tony Garnock-Jones and Matthias Felleisen Northeastern University, Boston, Massachusetts, USA Abstract. Most programs interact with the world: via graphical user interfaces, networks, etc. This form of interactivity entails concurrency, and concurrent program components must coordinate their computa- tions. This paper presents Syndicate, a novel design for a coordinated, concurrent programming language. Each concurrent component in Syn- dicate is a functional actor that participates in scoped conversations. The medium of conversation arranges for message exchanges and coor- dinates access to common knowledge. As such, Syndicate occupies a novel point in this design space, halfway between actors and threads. 1 From Interaction to Concurrency and Coordination Most programs must interact with their context. Interactions often start as re- actions to external events, such as a user’s gesture or the arrival of a message. Because nobody coordinates the multitude of external events, a program must notice and react to events in a concurrent manner. Thus, a sequential program must de-multiplex the sequence of events and launch the appropriate concurrent component for each event. Put differently, these interacting programs consist of concurrent components, even in sequential languages. Concurrent program components must coordinate their computations to re- alize the overall goals of the program. This coordination takes two forms: the exchange of knowledge and the establishment of frame conditions. In addition, coordination must take into account that reactions to events may call for the cre- ation of new concurrent components or that existing components may disappear due to exceptions or partial failures. In short, coordination poses a major prob- lem to the proper design of effective communicating, concurrent components.
    [Show full text]
  • Homotopical Patch Theory
    Homotopical Patch Theory Carlo Angiuli ∗ Ed Morehouse∗ Daniel R. Licata Carnegie Mellon University Carnegie Mellon University Wesleyan University [email protected] [email protected] [email protected] Robert Harper∗ Carnegie Mellon University [email protected] Abstract identity type p =a=Ab q. The rules for the identity type allow one Homotopy type theory is an extension of Martin-Löf type the- to define the operations on paths that are considered in homotopy ory, based on a correspondence with homotopy theory and higher theory. These include identity paths refl : a = a (reflexivity of category theory. The propositional equality type becomes proof- equality), inverse paths ! p : b = a when p : a = b (symme- relevant, and acts like paths in a space. Higher inductive types are try of equality), and composition of paths q ◦ p : a = c when a new class of datatypes which are specified by constructors not p : a = b and q : b = c (transitivity of equality), as well as homo- only for points but also for paths. In this paper, we show how patch topies relating these operations (for example, refl ◦ p = p), and ho- theory in the style of the Darcs version control system can be de- motopies relating these homotopies, etc. This correspondence has veloped in homotopy type theory. We reformulate patch theory us- suggested several extensions to type theory. One is Voevodsky’s ing the tools of homotopy type theory, and clearly separate formal univalence axiom [16, 34], which describes the path structure of theories of patches from their interpretation in terms of basic revi- the universe (the type of small types).
    [Show full text]